人教版八年级数学上册11.2与三角形有关的角 自主达标测试题(word版含答案)
文档属性
| 名称 | 人教版八年级数学上册11.2与三角形有关的角 自主达标测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 248.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 17:18:05 | ||
图片预览

文档简介
2022-2023学年人教版八年级数学上册《11.2与三角形有关的角》自主达标测试题(附答案)
一.选择题(共10小题,满分40分)
1.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A+∠B=∠C
C.∠A=∠B=∠C D.∠A=2∠B=3∠C
2.如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O,若∠BCA=70°,则∠BOE的度数是( )
A.60° B.55° C.50° D.40°
3.如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是( )
A.100° B.110° C.115° D.120°
4.如图,在△ABC中,∠B=70°,沿图中虚线EF翻折,使得点B落在AC上的点D处,则∠1+∠2等于( )
A.160° B.150° C.140° D.110°
5.将一副三角板按如图位置摆放,若∠BDE=75°,则∠AMD的度数是( )
A.75° B.80° C.85° D.90°
6.将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是( )
A.15° B.20° C.25° D.30°
7.如图:Rt△ABC中,∠C=90°,CD⊥AB于D.图中与∠A互余的角有( )
A.0个 B.1个 C.2个 D.3个
8.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=∠BAC.
其中正确的结论有( )
A.5 B.4 C.3 D.2
9.如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2=∠3+∠4 B.∠1+∠2=∠4﹣∠3
C.∠1+∠4=∠2+∠3 D.∠1+∠4=∠2﹣∠3
10.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB; ②∠ADC=∠GCD;
③CA平分∠BCG; ④∠DFB=∠CGE.
其中正确的结论是( )
A.②③ B.①②④ C.①③④ D.①②③④
二.填空题(共6小题,满分30分)
11.如图,∠A=20°,∠B=40°,∠C=50°,则∠ADB的度数是 .
12.如图,∠ACD=120°,∠B=20°,则∠A的度数是 .
13.如图,BE是△ABC的角平分线,AD是△ABC的高,∠ABC=60°,则∠AOE= .
14.如图,BC⊥AE,垂足为C,过C作CD∥AB,若∠ECD=48°.则∠B= 度.
15.将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠EDB= °.
16.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P= °.
三.解答题(共6小题,满分50分)
17.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
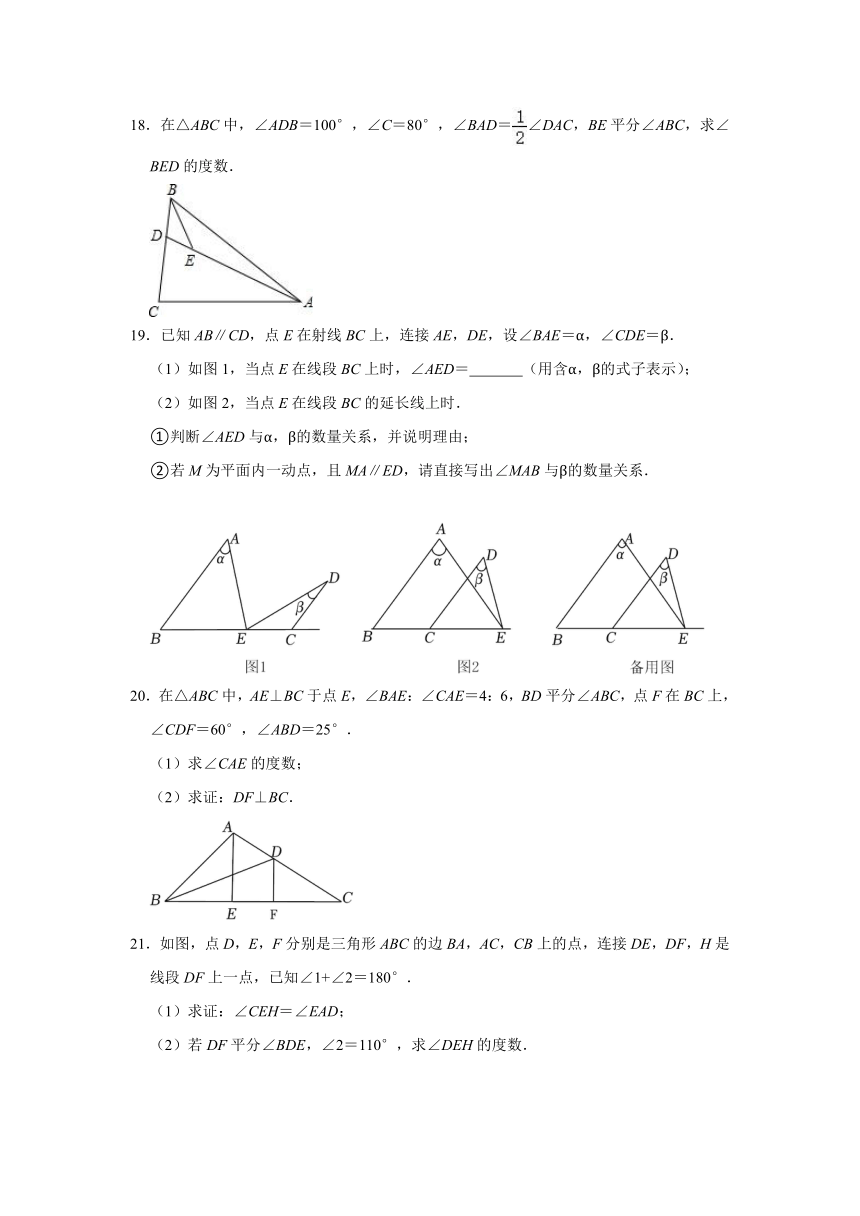
18.在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC,求∠BED的度数.
19.已知AB∥CD,点E在射线BC上,连接AE,DE,设∠BAE=α,∠CDE=β.
(1)如图1,当点E在线段BC上时,∠AED= (用含α,β的式子表示);
(2)如图2,当点E在线段BC的延长线上时.
①判断∠AED与α,β的数量关系,并说明理由;
②若M为平面内一动点,且MA∥ED,请直接写出∠MAB与β的数量关系.
20.在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:6,BD平分∠ABC,点F在BC上,∠CDF=60°,∠ABD=25°.
(1)求∠CAE的度数;
(2)求证:DF⊥BC.
21.如图,点D,E,F分别是三角形ABC的边BA,AC,CB上的点,连接DE,DF,H是线段DF上一点,已知∠1+∠2=180°.
(1)求证:∠CEH=∠EAD;
(2)若DF平分∠BDE,∠2=110°,求∠DEH的度数.
22.将一副三角板按照如图1所示的位置放置在直线EF上,现将含30°角的三角板OCD绕点O逆时针旋转180°,在这个过程中,
(1)如图2,当OD平分∠AOB,求∠BOC的度数;
(2)当OC在直线EF上方,且∠COE=30°时,求∠AOD的度数;
(3)若∠BOC=α,∠AOD=β,请直接写出α,β满足的数量关系.
参考答案
一.选择题(共10小题,满分40分)
1.解:A、最大角∠C=×180°=90°,是直角三角形,不符合题意;
B、最大角∠C=180°÷2=90°,是直角三角形,不符合题意;
C、设∠A=x,则∠B=2x,∠C=3x,
所以,x+2x+3x=180°,
解得x=30°,
最大角∠C=3×30°=90°,是直角三角形,不符合题意;
D、设∠A=x,则∠B=x,∠C=x,
所以,x+x+x=180°,
解得x=180°×>90°,是钝角三角形,符合题意.
故选:D.
2.解:∵BD⊥AC,
∴∠BDC=90°,
∵CE平分∠ACB,∠ACB=70°,
∴∠DCO=35°,
∴∠BOE=∠COD=90°﹣35°=55°,
故选:B.
3.解:∠ABC=50°,∠ACB=80°,
BP平分∠ABC,CP平分∠ACB,
∴∠PBC=25°,∠PCB=40°,
∴∠BPC=115°.
故选:C.
4.解:∵∠B=70°,
∴∠BEF+∠BFE=110°,
∵翻折,
∴∠BEF=∠DEF,∠BFE=∠DFE,
∴∠BED+∠BFD=2(∠BEF+∠BFE)=2×110°=220°,
∴∠1+∠2=180°×2﹣220°=140°,
故选:C.
5.解:∵∠B=60°,
∴∠A=30°,
∵∠BDE=75°,∠FDE=45°,
∴∠ADF=180°﹣75°﹣45°=60°,
∴∠AMD=180°﹣30°﹣60°=90°,
故选:D.
6.解:∵∠B=90°,∠A=45°,
∴∠ACB=45°.
∵∠EDF=90°,∠F=60°,
∴∠DEF=30°.
∵EF∥BC,
∴∠EDC=∠DEF=30°,
∴∠CED=∠ACB﹣∠EDC=45°﹣30°=15°.
故选:A.
7.解:∵∠A+∠ACD=90°,∠A+∠B=90°,
∴有2个,
故选:C.
8.解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°﹣∠ABD,∴③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°﹣∠ABC,
∴∠ADB不等于∠CDB,∴④错误;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴⑤正确;
即正确的有4个,
故选:B.
9.解:∵∠6是△ABC的外角,
∴∠1+∠4=∠6,﹣﹣﹣(1);
又∵∠2是△CDF的外角,
∴∠6=∠2﹣∠3,﹣﹣﹣(2);
由(1)(2)得:∠1+∠4=∠2﹣∠3.
故选:D.
10.解:∵EG∥BC,
∴∠CEG=∠BCA,
∵CD平分∠ACB,
∴∠BCA=2∠DCB,
∴∠CEG=2∠DCB,故①正确,
∵CG⊥EG,
∴∠G=90°,
∴∠GCE+∠CEG=90°,
∵∠A=90°,
∴∠BCA+∠ABC=90°,
∵∠CEG=∠ACB,
∴∠ECG=∠ABC,
∵∠ADC=∠ABC+∠DCB,∠GCD=∠ECG+∠ACD,∠ACD=∠DCB,
∴∠ADC=∠GCD,故②正确,
假设AC平分∠BCG,则∠ECG=∠ECB=∠CEG,
∴∠ECG=∠CEG=45°,显然不符合题意,故③错误,
∵∠DFB=∠FCB+∠FBC=(∠ACB+∠ABC)=45°,∠CGE=45°,
∴∠DFB=∠CGE,故④正确,
故选:B.
二.填空题(共6小题,满分30分)
11.解:∵∠A=20°,∠C=50°,
∴∠AEB=∠A+∠C=70°,
∵∠B=40°,
∴∠ADB=∠AEB+∠B=70°+40°=110°,
故答案为:110°.
12.解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B
=120°﹣20°
=100°.
故答案为100°.
13.解:∵BE是△ABC的角平分线,∠ABC=60°,
∴∠DOB=∠ABC=×60°=30°,
∵AD是△ABC的高,
∴∠ADC=90°,
∵∠ADC是△OBD的外角,
∴∠BOD=∠ADC﹣∠OBD=90°﹣30°=60°,
∴∠AOE=∠BOD=60°.
故答案为:60°.
14.解:∵CD∥AB,∠ECD=48°,
∴∠A=∠ECD=48°,
∵BC⊥AE,
∴∠B=90°﹣∠A=42°.
15.解:∵∠ACB=90°,∠A=30°,
∴∠ABC=90°﹣30°=60°,
∵∠ABC=∠F+∠BDF,∠F=45°,
∴∠BDF=∠ABC﹣∠F=60°﹣45°=15°,
∵∠EDF=90°,
∴∠EDB=∠EDF﹣∠BDF=90°﹣15°=75°,
故答案为75.
16.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°,
故答案为:30°.
三.解答题(共6小题,满分50分)
17.解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
18.解:∵∠ADB=100°,∠C=80°,
∴∠DAC=∠ADB﹣∠C=100°﹣80°=20°,
∵∠BAD=∠DAC,
∴∠BAD=×20°=10°,
在△ABD中,∠ABC=180°﹣∠ADB﹣∠BAD=180°﹣100°﹣10°=70°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=×70°=35°,
∴∠BED=∠BAD+∠ABE=10°+35°=45°.
19.解:(1)如图,过点E作EF∥AB,
∴则EF∥AB∥CD,
∴∠AEF=∠BAE=α,∠DEF=∠D=β,
∴∠AED=∠AEF+∠DEF=α+β;
故答案为:α+β;
(2)①如图,过点E作EF∥AB,
∴EF∥AB∥CD,
∴∠AEF=∠BAE=α,∠DEF=∠D=β,
∴∠AED=∠AEF+∠DEF=α﹣β;
②当点MA在A的下方时:
∵MA∥ED,AB∥CD,
∴∠BAM=∠CFM,∠CFM=∠D=β.
∴∠BAM=β.
当点MA在A的上方时:
有:∠M′AB+∠BAM=180°,
∴∠M′AB=180°﹣β;
所以∠MAB与β相等或互补.
20.(1)解:∵BD平分∠ABC,∠ABD=25°,
∴∠ABC=2∠ABD=50°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=40°,
又∵∠BAE:∠CAE=4:6,
∴∠CAE=60°;
(2)证明:∵∠CDF=60°,∠CAE=60°,
∴∠CAE=∠CDF,
∴DF∥AE,
又∵AE⊥BC,
∴DF⊥BC.
21.(1)证明:∵∠1+∠2=180°,∠DHE+∠2=180°,
∴∠1=∠DHE,
∴HE∥AB,
∴∠CEH=∠EAD;
(2)解:∵∠1+∠2=180°,∠2=110°,
∴∠1=70°,
∵DF平分∠BDE,
∴∠EDH=∠1=70°,
∵∠2=∠EDH+∠DEH,
∴∠DEH=40°.
22.解:∵OD平分∠AOB,
∴∠AOD=∠DOB=22.5°,
又∵∠COD=90°,
∴∠BOC=∠COD+∠DOB=90°+22.5°=112.5°;
(2)如图,
∵∠BOA+∠AOD+∠DOC+∠COE=180°,
∴∠AOD=180°﹣90°﹣45°=15°;
(3)当∠AOD在∠AOB内部时,α+β=45°+90°=135°,
当∠AOD在∠AOB外部时,
①旋转角大于45°而小于90°,α﹣β=135°,
②旋转角大于90°而小于180°,α+β=225°,
一.选择题(共10小题,满分40分)
1.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3 B.∠A+∠B=∠C
C.∠A=∠B=∠C D.∠A=2∠B=3∠C
2.如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O,若∠BCA=70°,则∠BOE的度数是( )
A.60° B.55° C.50° D.40°
3.如图,在△ABC中,∠ABC=50°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是( )
A.100° B.110° C.115° D.120°
4.如图,在△ABC中,∠B=70°,沿图中虚线EF翻折,使得点B落在AC上的点D处,则∠1+∠2等于( )
A.160° B.150° C.140° D.110°
5.将一副三角板按如图位置摆放,若∠BDE=75°,则∠AMD的度数是( )
A.75° B.80° C.85° D.90°
6.将一副三角尺按如图摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是( )
A.15° B.20° C.25° D.30°
7.如图:Rt△ABC中,∠C=90°,CD⊥AB于D.图中与∠A互余的角有( )
A.0个 B.1个 C.2个 D.3个
8.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°﹣∠ABD;
④BD平分∠ADC;
⑤∠BDC=∠BAC.
其中正确的结论有( )
A.5 B.4 C.3 D.2
9.如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2=∠3+∠4 B.∠1+∠2=∠4﹣∠3
C.∠1+∠4=∠2+∠3 D.∠1+∠4=∠2﹣∠3
10.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB; ②∠ADC=∠GCD;
③CA平分∠BCG; ④∠DFB=∠CGE.
其中正确的结论是( )
A.②③ B.①②④ C.①③④ D.①②③④
二.填空题(共6小题,满分30分)
11.如图,∠A=20°,∠B=40°,∠C=50°,则∠ADB的度数是 .
12.如图,∠ACD=120°,∠B=20°,则∠A的度数是 .
13.如图,BE是△ABC的角平分线,AD是△ABC的高,∠ABC=60°,则∠AOE= .
14.如图,BC⊥AE,垂足为C,过C作CD∥AB,若∠ECD=48°.则∠B= 度.
15.将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠EDB= °.
16.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P= °.
三.解答题(共6小题,满分50分)
17.如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
18.在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC,求∠BED的度数.
19.已知AB∥CD,点E在射线BC上,连接AE,DE,设∠BAE=α,∠CDE=β.
(1)如图1,当点E在线段BC上时,∠AED= (用含α,β的式子表示);
(2)如图2,当点E在线段BC的延长线上时.
①判断∠AED与α,β的数量关系,并说明理由;
②若M为平面内一动点,且MA∥ED,请直接写出∠MAB与β的数量关系.
20.在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:6,BD平分∠ABC,点F在BC上,∠CDF=60°,∠ABD=25°.
(1)求∠CAE的度数;
(2)求证:DF⊥BC.
21.如图,点D,E,F分别是三角形ABC的边BA,AC,CB上的点,连接DE,DF,H是线段DF上一点,已知∠1+∠2=180°.
(1)求证:∠CEH=∠EAD;
(2)若DF平分∠BDE,∠2=110°,求∠DEH的度数.
22.将一副三角板按照如图1所示的位置放置在直线EF上,现将含30°角的三角板OCD绕点O逆时针旋转180°,在这个过程中,
(1)如图2,当OD平分∠AOB,求∠BOC的度数;
(2)当OC在直线EF上方,且∠COE=30°时,求∠AOD的度数;
(3)若∠BOC=α,∠AOD=β,请直接写出α,β满足的数量关系.
参考答案
一.选择题(共10小题,满分40分)
1.解:A、最大角∠C=×180°=90°,是直角三角形,不符合题意;
B、最大角∠C=180°÷2=90°,是直角三角形,不符合题意;
C、设∠A=x,则∠B=2x,∠C=3x,
所以,x+2x+3x=180°,
解得x=30°,
最大角∠C=3×30°=90°,是直角三角形,不符合题意;
D、设∠A=x,则∠B=x,∠C=x,
所以,x+x+x=180°,
解得x=180°×>90°,是钝角三角形,符合题意.
故选:D.
2.解:∵BD⊥AC,
∴∠BDC=90°,
∵CE平分∠ACB,∠ACB=70°,
∴∠DCO=35°,
∴∠BOE=∠COD=90°﹣35°=55°,
故选:B.
3.解:∠ABC=50°,∠ACB=80°,
BP平分∠ABC,CP平分∠ACB,
∴∠PBC=25°,∠PCB=40°,
∴∠BPC=115°.
故选:C.
4.解:∵∠B=70°,
∴∠BEF+∠BFE=110°,
∵翻折,
∴∠BEF=∠DEF,∠BFE=∠DFE,
∴∠BED+∠BFD=2(∠BEF+∠BFE)=2×110°=220°,
∴∠1+∠2=180°×2﹣220°=140°,
故选:C.
5.解:∵∠B=60°,
∴∠A=30°,
∵∠BDE=75°,∠FDE=45°,
∴∠ADF=180°﹣75°﹣45°=60°,
∴∠AMD=180°﹣30°﹣60°=90°,
故选:D.
6.解:∵∠B=90°,∠A=45°,
∴∠ACB=45°.
∵∠EDF=90°,∠F=60°,
∴∠DEF=30°.
∵EF∥BC,
∴∠EDC=∠DEF=30°,
∴∠CED=∠ACB﹣∠EDC=45°﹣30°=15°.
故选:A.
7.解:∵∠A+∠ACD=90°,∠A+∠B=90°,
∴有2个,
故选:C.
8.解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正确;
在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°﹣∠ABD,∴③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°﹣∠ABC,
∴∠ADB不等于∠CDB,∴④错误;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴⑤正确;
即正确的有4个,
故选:B.
9.解:∵∠6是△ABC的外角,
∴∠1+∠4=∠6,﹣﹣﹣(1);
又∵∠2是△CDF的外角,
∴∠6=∠2﹣∠3,﹣﹣﹣(2);
由(1)(2)得:∠1+∠4=∠2﹣∠3.
故选:D.
10.解:∵EG∥BC,
∴∠CEG=∠BCA,
∵CD平分∠ACB,
∴∠BCA=2∠DCB,
∴∠CEG=2∠DCB,故①正确,
∵CG⊥EG,
∴∠G=90°,
∴∠GCE+∠CEG=90°,
∵∠A=90°,
∴∠BCA+∠ABC=90°,
∵∠CEG=∠ACB,
∴∠ECG=∠ABC,
∵∠ADC=∠ABC+∠DCB,∠GCD=∠ECG+∠ACD,∠ACD=∠DCB,
∴∠ADC=∠GCD,故②正确,
假设AC平分∠BCG,则∠ECG=∠ECB=∠CEG,
∴∠ECG=∠CEG=45°,显然不符合题意,故③错误,
∵∠DFB=∠FCB+∠FBC=(∠ACB+∠ABC)=45°,∠CGE=45°,
∴∠DFB=∠CGE,故④正确,
故选:B.
二.填空题(共6小题,满分30分)
11.解:∵∠A=20°,∠C=50°,
∴∠AEB=∠A+∠C=70°,
∵∠B=40°,
∴∠ADB=∠AEB+∠B=70°+40°=110°,
故答案为:110°.
12.解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B
=120°﹣20°
=100°.
故答案为100°.
13.解:∵BE是△ABC的角平分线,∠ABC=60°,
∴∠DOB=∠ABC=×60°=30°,
∵AD是△ABC的高,
∴∠ADC=90°,
∵∠ADC是△OBD的外角,
∴∠BOD=∠ADC﹣∠OBD=90°﹣30°=60°,
∴∠AOE=∠BOD=60°.
故答案为:60°.
14.解:∵CD∥AB,∠ECD=48°,
∴∠A=∠ECD=48°,
∵BC⊥AE,
∴∠B=90°﹣∠A=42°.
15.解:∵∠ACB=90°,∠A=30°,
∴∠ABC=90°﹣30°=60°,
∵∠ABC=∠F+∠BDF,∠F=45°,
∴∠BDF=∠ABC﹣∠F=60°﹣45°=15°,
∵∠EDF=90°,
∴∠EDB=∠EDF﹣∠BDF=90°﹣15°=75°,
故答案为75.
16.解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,
∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,
∵∠PCM是△BCP的外角,
∴∠P=∠PCM﹣∠CBP=50°﹣20°=30°,
故答案为:30°.
三.解答题(共6小题,满分50分)
17.解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
18.解:∵∠ADB=100°,∠C=80°,
∴∠DAC=∠ADB﹣∠C=100°﹣80°=20°,
∵∠BAD=∠DAC,
∴∠BAD=×20°=10°,
在△ABD中,∠ABC=180°﹣∠ADB﹣∠BAD=180°﹣100°﹣10°=70°,
∵BE平分∠ABC,
∴∠ABE=∠ABC=×70°=35°,
∴∠BED=∠BAD+∠ABE=10°+35°=45°.
19.解:(1)如图,过点E作EF∥AB,
∴则EF∥AB∥CD,
∴∠AEF=∠BAE=α,∠DEF=∠D=β,
∴∠AED=∠AEF+∠DEF=α+β;
故答案为:α+β;
(2)①如图,过点E作EF∥AB,
∴EF∥AB∥CD,
∴∠AEF=∠BAE=α,∠DEF=∠D=β,
∴∠AED=∠AEF+∠DEF=α﹣β;
②当点MA在A的下方时:
∵MA∥ED,AB∥CD,
∴∠BAM=∠CFM,∠CFM=∠D=β.
∴∠BAM=β.
当点MA在A的上方时:
有:∠M′AB+∠BAM=180°,
∴∠M′AB=180°﹣β;
所以∠MAB与β相等或互补.
20.(1)解:∵BD平分∠ABC,∠ABD=25°,
∴∠ABC=2∠ABD=50°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=40°,
又∵∠BAE:∠CAE=4:6,
∴∠CAE=60°;
(2)证明:∵∠CDF=60°,∠CAE=60°,
∴∠CAE=∠CDF,
∴DF∥AE,
又∵AE⊥BC,
∴DF⊥BC.
21.(1)证明:∵∠1+∠2=180°,∠DHE+∠2=180°,
∴∠1=∠DHE,
∴HE∥AB,
∴∠CEH=∠EAD;
(2)解:∵∠1+∠2=180°,∠2=110°,
∴∠1=70°,
∵DF平分∠BDE,
∴∠EDH=∠1=70°,
∵∠2=∠EDH+∠DEH,
∴∠DEH=40°.
22.解:∵OD平分∠AOB,
∴∠AOD=∠DOB=22.5°,
又∵∠COD=90°,
∴∠BOC=∠COD+∠DOB=90°+22.5°=112.5°;
(2)如图,
∵∠BOA+∠AOD+∠DOC+∠COE=180°,
∴∠AOD=180°﹣90°﹣45°=15°;
(3)当∠AOD在∠AOB内部时,α+β=45°+90°=135°,
当∠AOD在∠AOB外部时,
①旋转角大于45°而小于90°,α﹣β=135°,
②旋转角大于90°而小于180°,α+β=225°,
