人教版数学九年级上册22.3实际问题与二次函数同步练习 (含答案)
文档属性
| 名称 | 人教版数学九年级上册22.3实际问题与二次函数同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 16:45:25 | ||
图片预览



文档简介
22.3 实际问题与二次函数
班级: 姓名: 成绩:
一、选择题
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
2.如图,抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内(含边界),且该抛物线经过原点O(0,0),则a的取值范围是( )
A.-2≤a≤-1 B. C. D.
3.如图,等腰与矩形DEFG在同一水平线上,,现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A. B.
C. D.
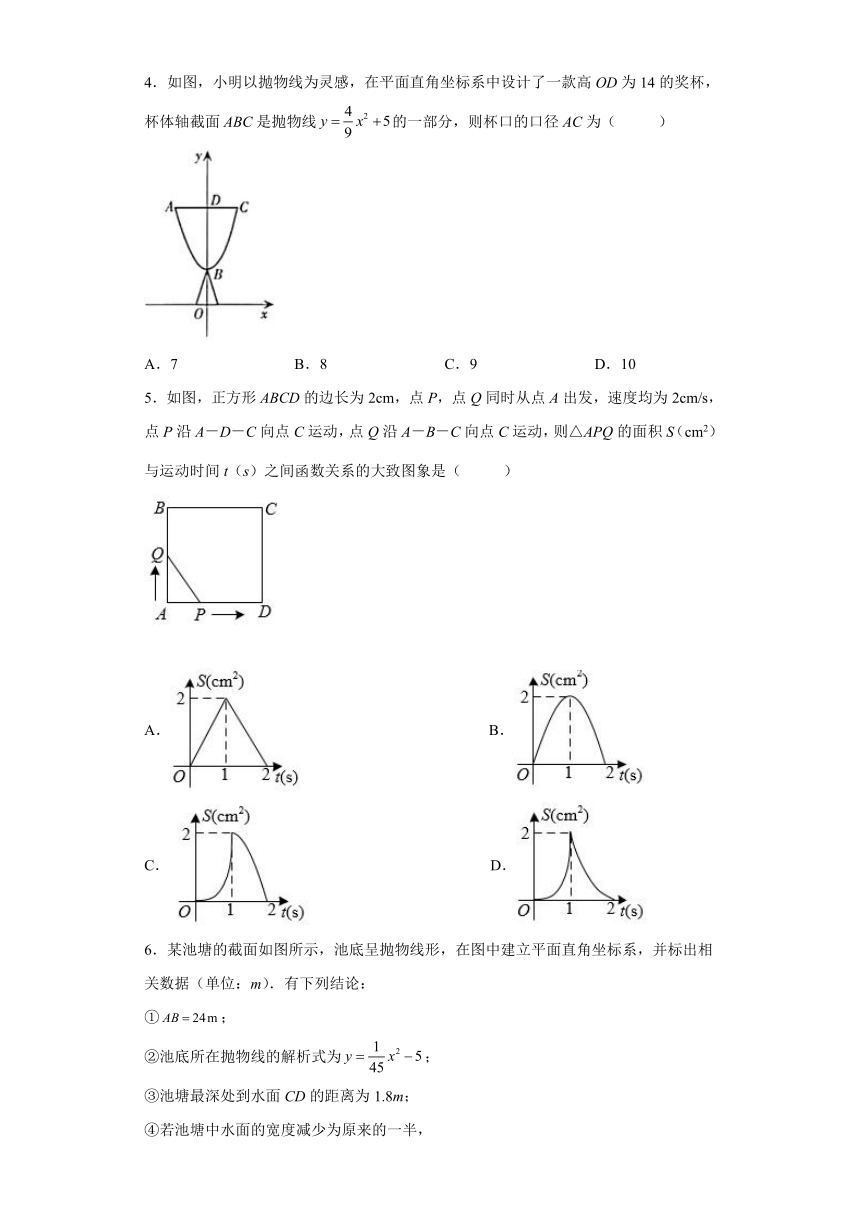
4.如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线的一部分,则杯口的口径AC为( )
A.7 B.8 C.9 D.10
5.如图,正方形ABCD的边长为2cm,点P,点Q同时从点A出发,速度均为2cm/s,点P沿A-D-C向点C运动,点Q沿A-B-C向点C运动,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )
B.
C. D.
6.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:
①;
②池底所在抛物线的解析式为;
③池塘最深处到水面CD的距离为1.8m;
④若池塘中水面的宽度减少为原来的一半,
则最深处到水面的距离减少为原来的.其中结论正确的是( )
A.①② B.②④ C.③④ D.①④
7.某商品现在的售价为每件35元,每天可卖出50件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,求最大销售额是( )
A.2500元 B.2000元 C.1800元 D.2200元
8.2020年6月中旬以来,北京市新冠肺炎疫情出现反弹,北京市民对防疫物资需求量激增.某厂商计划投资产销一种消毒液,设每天产销量为x瓶,每日产销这种消毒液的有关信息如下表:(产销量指生产并销售的数量,生产多少就销售多少,不考虑滞销和脱销)若该消毒液的单日产销利润y元,当销量x为多少时,该消毒液的单日产销利润最大.( )
消毒液 每瓶售价(元) 每瓶成本(元) 每日其他费用(元) 每日最大产销量(瓶)
30 18 1200+0.02x2 250
A.250 B.300 C.200 D.550
9.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是;
②小球运动的时间为;
③小球抛出3秒时,速度为0:
④当时,小球的高度.
其中正确的是( )
A.②③ B.②③④ C.①②④ D.①③④
10.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m,则该水流距水平面的最大高度AD的长度为( )
A.9m B.10m C.11m D.12m
11.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
12.飞机着陆后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数表达式为,当滑行时间为10秒时,滑行距离为450米;当滑行时间为20秒时,滑行距离为600米,则飞机的最大滑行距离为( )
A.600米 B.800米 C.1000米 D.1200米
13.已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数图像的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A.0米到3米 B.5米到8米 C.到8米 D.5米到米
14.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,点A,B,C为该抛物线上的三点,如图y表示运行的竖直高度(单位:m),x表示水平距离(单位:m).由此可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.4 B.5 C.7 D.9
15.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.那么当运动员滑出点A后,运动员运动的水平距离为( )米时,运动员与小山坡的竖直距离为20米.
A.50 B. C. D.
二、填空题
16.用总长为60m的篱笆围成长方形场地,长方形的面积S(m2)与一边长l(m)之间的函数关系式为___________,自变量l的取值范围是__________.
17.如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
18.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10m.如果水位以0.25m/h的速度上涨,那么达到警戒水位后,再过________h水位达到桥拱最高点O.
19.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
20.某游乐场的圆形喷水池中心O有一雕塑OA,从点A向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y(x﹣5)2+6
(1)雕塑高OA的值是____m;
(2)落水点C,D之间的距离是____m.
三、解答题
21.如图,抛物线与x轴交于A(-2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点E,点D的横坐标为4.
(1)求抛物线的解析式与直线l的解析式;
(2)若点P是抛物线上的点且在直线l上方,连接PA、PD,求当ΔPAD面积最大时点P的坐标及该面积的最大值;
(3)若点Q是x轴上的点,且∠ADQ=45°,请直接写出点Q的坐标.
22.新型建材(即新型建筑材料)是区别于传统的砖瓦、灰砂石等建材的建筑材料新品种,行业内将新型建筑材料的范围作了明确的界定,即新型建筑材料主要包括新型墙体材料、新型防水保温隔热密封材料和装饰装修材料三大类,某开发商承建一精密实验室,要求全部使用新型建筑材料,经调查发现:新型建筑材料总成本包括装饰装修材料成本、新型墙体材料成本和新型防水保温隔热密封材料成本,其中装饰装修材料成本固定不变为100万元,新型墙体材料成本与建筑面积x(m2)成正比,新型防水保温隔热密封材料成本与建筑面积x(m2)的平方成正比,在建筑过程中,设新型建筑材料总成本为y(万元),获得如下数据:
x(单位:m2) 20 50
y(单位:万元) 240 600
(1)求新型建筑材料总成本为y(万元)与建筑面积x(m2)的函数表达式;
(2)在建筑过型中,开发商测算出此的时每平方米的平均成本为12万元,求此时完成的建筑面积;
(3)设建设该厂房每平方米的毛利润为Q(万元)且有Q=kx+b(k≠0),已知当x=50时,Q为12.5万元,且此时开发商总纯利润W最大,求k、b的值.(纯利润=毛利润﹣成本)
23.某乒乓球馆使用发球机进行辅助训练,出球口A位于桌面BC左上方,桌面BC的长为2.74m.过点A作OA⊥BC,垂足为O,OB=0.03m,以点O为原点,以直线BC为x轴,OA所在直线为y轴,建立平面直角坐标系,如图所示,从出球口A发出的乒乓球运动路线为抛物线的一部分L,设乒乓球与出球口A的水平距离为x(m),到桌面的高度为y(m),运行时间为t(s),在桌面上的落点为D,经测试,得到如下部分数据:
t(s) 0 0.2 0.4 0.6 0.8 ...
x(m) 0 0.5 1 1.5 2 ...
y(m) 0.25 0.4 0.45 0.4 0.25 ...
(1)当t= s时,乒乓球达到最大高度;猜想y与x之间是否存在二次函数关系,如果存在,求出函数关系式;如果不存在,请说明理由;
(2)桌面正中间位置安装的球网GH的高度为0.15m,求乒乓球从出球口A发出经过多长时间位于球网正上方,此时乒乓球到球网顶端H的距离约为多少?(结果保留两位小数)
(3)乒乓球落在点D后随即弹起,沿抛物线:y=﹣0.5(x﹣p)(x﹣3.5)的路线运动,小明拿球拍EF与桌面夹角为60°接球,球拍中心线EF长为0.16m,下沿E在x轴上,假设抛物线L,与EF在同一平面内,且乒乓球落在EF上(含端点,点E在点C右侧),求p的值,并直接写出EF到桌边的距离CE的取值范围.
参考答案
1.D
2.D
3.B
4.C
5.C
6.B
7.C
8.D
9.B
10.A
11.A
12.A
13.B
14.C
15.C
16. 0<l<30
17.8
18.
19.2
20.##1 22
21.(1)抛物线的解析式为,直线l的解析式为;
(2)点P的坐标为(1,),该面积的最大值为.
(3)(13,0)或(3,0)
22.(1)
(2)此时完成的建筑面积为20或50;
(3)
23.(1)0.4;y与x之间存在二次函数关系,
(2)乒乓球从出球口A发出经过0.56s时间位于球网正上方,此时乒乓球到球网顶端H的距离约0.27m;
(3)2.5;
班级: 姓名: 成绩:
一、选择题
1.两个正方形的周长和是10,如果其中一个正方形的边长为,则这两个正方形的面积的和S关于的函数关系式为( )
A. B.
C. D.
2.如图,抛物线y=ax2+bx+c的顶点M在矩形ABCD区域内(含边界),且该抛物线经过原点O(0,0),则a的取值范围是( )
A.-2≤a≤-1 B. C. D.
3.如图,等腰与矩形DEFG在同一水平线上,,现将等腰沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为( )
A. B.
C. D.
4.如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线的一部分,则杯口的口径AC为( )
A.7 B.8 C.9 D.10
5.如图,正方形ABCD的边长为2cm,点P,点Q同时从点A出发,速度均为2cm/s,点P沿A-D-C向点C运动,点Q沿A-B-C向点C运动,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )
B.
C. D.
6.某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:
①;
②池底所在抛物线的解析式为;
③池塘最深处到水面CD的距离为1.8m;
④若池塘中水面的宽度减少为原来的一半,
则最深处到水面的距离减少为原来的.其中结论正确的是( )
A.①② B.②④ C.③④ D.①④
7.某商品现在的售价为每件35元,每天可卖出50件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,求最大销售额是( )
A.2500元 B.2000元 C.1800元 D.2200元
8.2020年6月中旬以来,北京市新冠肺炎疫情出现反弹,北京市民对防疫物资需求量激增.某厂商计划投资产销一种消毒液,设每天产销量为x瓶,每日产销这种消毒液的有关信息如下表:(产销量指生产并销售的数量,生产多少就销售多少,不考虑滞销和脱销)若该消毒液的单日产销利润y元,当销量x为多少时,该消毒液的单日产销利润最大.( )
消毒液 每瓶售价(元) 每瓶成本(元) 每日其他费用(元) 每日最大产销量(瓶)
30 18 1200+0.02x2 250
A.250 B.300 C.200 D.550
9.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是;
②小球运动的时间为;
③小球抛出3秒时,速度为0:
④当时,小球的高度.
其中正确的是( )
A.②③ B.②③④ C.①②④ D.①③④
10.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m,则该水流距水平面的最大高度AD的长度为( )
A.9m B.10m C.11m D.12m
11.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是( )
A. B. C. D.
12.飞机着陆后滑行的距离s(单位:米)关于滑行时间t(单位:秒)的函数表达式为,当滑行时间为10秒时,滑行距离为450米;当滑行时间为20秒时,滑行距离为600米,则飞机的最大滑行距离为( )
A.600米 B.800米 C.1000米 D.1200米
13.已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数图像的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A.0米到3米 B.5米到8米 C.到8米 D.5米到米
14.过山车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,点A,B,C为该抛物线上的三点,如图y表示运行的竖直高度(单位:m),x表示水平距离(单位:m).由此可推断出,此过山车运行到最低点时,所对应的水平距离x可能为( )
A.4 B.5 C.7 D.9
15.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.那么当运动员滑出点A后,运动员运动的水平距离为( )米时,运动员与小山坡的竖直距离为20米.
A.50 B. C. D.
二、填空题
16.用总长为60m的篱笆围成长方形场地,长方形的面积S(m2)与一边长l(m)之间的函数关系式为___________,自变量l的取值范围是__________.
17.如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
18.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10m.如果水位以0.25m/h的速度上涨,那么达到警戒水位后,再过________h水位达到桥拱最高点O.
19.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
20.某游乐场的圆形喷水池中心O有一雕塑OA,从点A向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y(x﹣5)2+6
(1)雕塑高OA的值是____m;
(2)落水点C,D之间的距离是____m.
三、解答题
21.如图,抛物线与x轴交于A(-2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点E,点D的横坐标为4.
(1)求抛物线的解析式与直线l的解析式;
(2)若点P是抛物线上的点且在直线l上方,连接PA、PD,求当ΔPAD面积最大时点P的坐标及该面积的最大值;
(3)若点Q是x轴上的点,且∠ADQ=45°,请直接写出点Q的坐标.
22.新型建材(即新型建筑材料)是区别于传统的砖瓦、灰砂石等建材的建筑材料新品种,行业内将新型建筑材料的范围作了明确的界定,即新型建筑材料主要包括新型墙体材料、新型防水保温隔热密封材料和装饰装修材料三大类,某开发商承建一精密实验室,要求全部使用新型建筑材料,经调查发现:新型建筑材料总成本包括装饰装修材料成本、新型墙体材料成本和新型防水保温隔热密封材料成本,其中装饰装修材料成本固定不变为100万元,新型墙体材料成本与建筑面积x(m2)成正比,新型防水保温隔热密封材料成本与建筑面积x(m2)的平方成正比,在建筑过程中,设新型建筑材料总成本为y(万元),获得如下数据:
x(单位:m2) 20 50
y(单位:万元) 240 600
(1)求新型建筑材料总成本为y(万元)与建筑面积x(m2)的函数表达式;
(2)在建筑过型中,开发商测算出此的时每平方米的平均成本为12万元,求此时完成的建筑面积;
(3)设建设该厂房每平方米的毛利润为Q(万元)且有Q=kx+b(k≠0),已知当x=50时,Q为12.5万元,且此时开发商总纯利润W最大,求k、b的值.(纯利润=毛利润﹣成本)
23.某乒乓球馆使用发球机进行辅助训练,出球口A位于桌面BC左上方,桌面BC的长为2.74m.过点A作OA⊥BC,垂足为O,OB=0.03m,以点O为原点,以直线BC为x轴,OA所在直线为y轴,建立平面直角坐标系,如图所示,从出球口A发出的乒乓球运动路线为抛物线的一部分L,设乒乓球与出球口A的水平距离为x(m),到桌面的高度为y(m),运行时间为t(s),在桌面上的落点为D,经测试,得到如下部分数据:
t(s) 0 0.2 0.4 0.6 0.8 ...
x(m) 0 0.5 1 1.5 2 ...
y(m) 0.25 0.4 0.45 0.4 0.25 ...
(1)当t= s时,乒乓球达到最大高度;猜想y与x之间是否存在二次函数关系,如果存在,求出函数关系式;如果不存在,请说明理由;
(2)桌面正中间位置安装的球网GH的高度为0.15m,求乒乓球从出球口A发出经过多长时间位于球网正上方,此时乒乓球到球网顶端H的距离约为多少?(结果保留两位小数)
(3)乒乓球落在点D后随即弹起,沿抛物线:y=﹣0.5(x﹣p)(x﹣3.5)的路线运动,小明拿球拍EF与桌面夹角为60°接球,球拍中心线EF长为0.16m,下沿E在x轴上,假设抛物线L,与EF在同一平面内,且乒乓球落在EF上(含端点,点E在点C右侧),求p的值,并直接写出EF到桌边的距离CE的取值范围.
参考答案
1.D
2.D
3.B
4.C
5.C
6.B
7.C
8.D
9.B
10.A
11.A
12.A
13.B
14.C
15.C
16. 0<l<30
17.8
18.
19.2
20.##1 22
21.(1)抛物线的解析式为,直线l的解析式为;
(2)点P的坐标为(1,),该面积的最大值为.
(3)(13,0)或(3,0)
22.(1)
(2)此时完成的建筑面积为20或50;
(3)
23.(1)0.4;y与x之间存在二次函数关系,
(2)乒乓球从出球口A发出经过0.56s时间位于球网正上方,此时乒乓球到球网顶端H的距离约0.27m;
(3)2.5;
同课章节目录
