2022苏科版数学七年级上册2.4 绝对值与相反数 课件 (共31张PPT)
文档属性
| 名称 | 2022苏科版数学七年级上册2.4 绝对值与相反数 课件 (共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 751.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
第三讲
相反数
课程大纲
01
02
03
04
相反数的定义
和求法
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
1
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
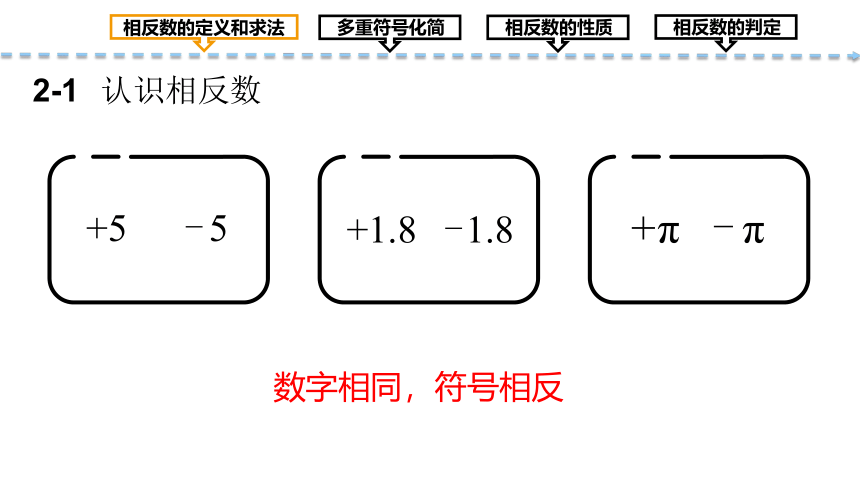
认识相反数
2-1
数字相同,符号相反
相反数的定义和求法
多重符号化简
相反数的性质
相反数的判定
认识相反数:什么是认识相反数
多重符号化简
相反数的性质
相反数的判定
求一个数的相反数,
只需 即可.
像 和 , 和 , 和 这样
只有符号不同的两个数互为相反数,其中一个是另一个的相反数.
定义
任意一个正数都能找到和它对应的相反数吗?
任意负数呢?
0?
0的相反数是0
记笔记
认识相反数:什么是认识相反数
相反数的定义和求法
多重符号化简
相反数的性质
相反数的判定
1
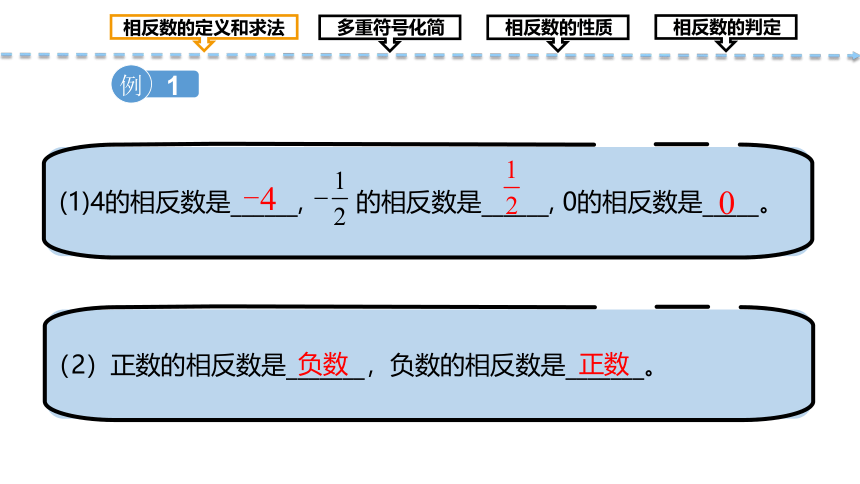
例
(1)4的相反数是______, 的相反数是______, 0的相反数是_____。
(2)正数的相反数是_______,负数的相反数是_______。
负数
正数
相反数的定义和求法
求一个数的相反数,
只需 即可.
求一个数的相反数,只需 即可.
加上“ ”号并化简
思考1:怎么求一个数的相反数?
认识相反数:如何求一个数的相反数
例.求 的相反数 :
记笔记
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
(2)_____的相反数是 4,0的相反数是____, 的相反数是_____.
0
(1)下列各数中互为相反数的是( )
C
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
1
练
1、 的相反数是________;
2、 的相反数是________;
3、 的相反数是__________;
的相反数是________;
的相反数是__________;
的相反数是________;
的相反数是________;
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
2
例
的相反数是___________
的相反数是_____________
的相反数是___________
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
2
练
多重符号化简
2
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
多重符号化简问题
的相反数:
的相反数:
的相反数:
的相反数:
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
多重符号的化简:
只看“ ”的个数,奇负偶正
记笔记
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
多重符号化简问题
(1) 表示_____的相反数,即 =_____;
(2) 表示_____的相反数,即 =_____.
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
3
例
(1) 化简:
(2) 化简:
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
3
练
(1) 的相反数是________;
(2) 的相反数是________.
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
4
例
(1) =________; =________;
=_________; =_________.
(2) 的相反数是________.
(3) 的相反数是________.
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
4
练
相反数的性质
3
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
互为相反数的两个数相加等于0;
记笔记
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
相反数的性质
(1) 若 与 互为相反数,则 =_____.
(2) 若 的相反数是3,求 的值。
(3) 若 与 互为相反数,求 的值。
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
25
P
1
例
(1)如果 那么 两个数一定是( )
都等于0
一正一负
互为相反数
互为倒数
A.
B.
C.
D.
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
1
练
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
1
练
(2)若 与 互为相反数,则 =_____;
(3)若 与 互为相反数,则 =_____.
相反数的判定
4
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
若两个数和为0,则这两个数互为相反数。
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
相反数的判定
下列各代数式:
与
③
②
④
与
与
①
与
其中互为相反数的有( )
A.
B.
C.
D.
①②
②④
②③④
①②③④
B
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
2
例
若 , 互为相反数,则下面互为相反数的是( )
A. 和
B. 和
C. 和
D. 和
B
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
2
练
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
3
例
√
×
×
√
√
×
判断下列说法是否正确,正确的打”√",错误的打”x"
( )(1)正数的相反数是负数,负数的相反数是正数
( )(2)在数轴上,和原点距离相等的两个点所表示的数一定互为相反数
( )(3)符号不同的两个数互为相反数
( )(4)两个数互为相反数,则这两个数有可能相等
( )(5)若a、b互为相反数,则a+b=0a
( )(6)若a、b互为相反数,则=-1b
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
3
练
×
×
√
√
√
√
1.相反数的定义:只有符号不同的两个数互为相反数。
2.求相反数:加“ ”并化简
3.多重符号化简:“ ”的个数,奇负偶正
4.相反数 和为
性质
判定
课堂总结
谢谢观看
不念过去,不畏将来,只活在当下
第三讲
相反数
课程大纲
01
02
03
04
相反数的定义
和求法
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
1
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
认识相反数
2-1
数字相同,符号相反
相反数的定义和求法
多重符号化简
相反数的性质
相反数的判定
认识相反数:什么是认识相反数
多重符号化简
相反数的性质
相反数的判定
求一个数的相反数,
只需 即可.
像 和 , 和 , 和 这样
只有符号不同的两个数互为相反数,其中一个是另一个的相反数.
定义
任意一个正数都能找到和它对应的相反数吗?
任意负数呢?
0?
0的相反数是0
记笔记
认识相反数:什么是认识相反数
相反数的定义和求法
多重符号化简
相反数的性质
相反数的判定
1
例
(1)4的相反数是______, 的相反数是______, 0的相反数是_____。
(2)正数的相反数是_______,负数的相反数是_______。
负数
正数
相反数的定义和求法
求一个数的相反数,
只需 即可.
求一个数的相反数,只需 即可.
加上“ ”号并化简
思考1:怎么求一个数的相反数?
认识相反数:如何求一个数的相反数
例.求 的相反数 :
记笔记
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
(2)_____的相反数是 4,0的相反数是____, 的相反数是_____.
0
(1)下列各数中互为相反数的是( )
C
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
1
练
1、 的相反数是________;
2、 的相反数是________;
3、 的相反数是__________;
的相反数是________;
的相反数是__________;
的相反数是________;
的相反数是________;
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
2
例
的相反数是___________
的相反数是_____________
的相反数是___________
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
2
练
多重符号化简
2
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
多重符号化简问题
的相反数:
的相反数:
的相反数:
的相反数:
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
多重符号的化简:
只看“ ”的个数,奇负偶正
记笔记
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
多重符号化简问题
(1) 表示_____的相反数,即 =_____;
(2) 表示_____的相反数,即 =_____.
多重符号化简
相反数的性质
相反数的判定
相反数的定义和求法
3
例
(1) 化简:
(2) 化简:
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
3
练
(1) 的相反数是________;
(2) 的相反数是________.
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
4
例
(1) =________; =________;
=_________; =_________.
(2) 的相反数是________.
(3) 的相反数是________.
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
4
练
相反数的性质
3
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
互为相反数的两个数相加等于0;
记笔记
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
相反数的性质
(1) 若 与 互为相反数,则 =_____.
(2) 若 的相反数是3,求 的值。
(3) 若 与 互为相反数,求 的值。
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
25
P
1
例
(1)如果 那么 两个数一定是( )
都等于0
一正一负
互为相反数
互为倒数
A.
B.
C.
D.
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
1
练
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
1
练
(2)若 与 互为相反数,则 =_____;
(3)若 与 互为相反数,则 =_____.
相反数的判定
4
相反数的定义和求法
01
相反数的判定
04
相反数的性质
03
多重符号化简
02
若两个数和为0,则这两个数互为相反数。
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
相反数的判定
下列各代数式:
与
③
②
④
与
与
①
与
其中互为相反数的有( )
A.
B.
C.
D.
①②
②④
②③④
①②③④
B
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
2
例
若 , 互为相反数,则下面互为相反数的是( )
A. 和
B. 和
C. 和
D. 和
B
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
2
练
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
3
例
√
×
×
√
√
×
判断下列说法是否正确,正确的打”√",错误的打”x"
( )(1)正数的相反数是负数,负数的相反数是正数
( )(2)在数轴上,和原点距离相等的两个点所表示的数一定互为相反数
( )(3)符号不同的两个数互为相反数
( )(4)两个数互为相反数,则这两个数有可能相等
( )(5)若a、b互为相反数,则a+b=0a
( )(6)若a、b互为相反数,则=-1b
相反数的性质
相反数的判定
相反数的定义和求法
多重符号化简
3
练
×
×
√
√
√
√
1.相反数的定义:只有符号不同的两个数互为相反数。
2.求相反数:加“ ”并化简
3.多重符号化简:“ ”的个数,奇负偶正
4.相反数 和为
性质
判定
课堂总结
谢谢观看
不念过去,不畏将来,只活在当下
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
