青海省西宁北外附属新华联外国语高级中学2022-2023学年高三上学期开学考试数学试题(含简略答案)
文档属性
| 名称 | 青海省西宁北外附属新华联外国语高级中学2022-2023学年高三上学期开学考试数学试题(含简略答案) |  | |
| 格式 | docx | ||
| 文件大小 | 302.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 01:13:41 | ||
图片预览


文档简介
北外西宁新华联国际学校2022-2023学年第一学期
开学摸底考试高三数学试卷
试卷分值:150 考试时间:120分钟
一、选择题(本题共计12小题,每题5分,共计60分)
1. 设集合,,则( )
A. B. C. D.
2. 下列函数既是奇函数又在(﹣1,1)上是减函数的是( )
A. B.
C. y=x﹣1 D. y=tanx
3. 已知两个不同的平面,和两条不同的直线,满足,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 设,,,则a,b,c的大小关系是
A. B. C. D.
5. 下列各命题中正确命题序号是
① “若都是奇数,则是偶数”的逆否命题是“不是偶数,则都不是奇数”;
② 命题“”的否定是“” ;
③ “函数的最小正周期为” 是“”的必要不充分条件;
④“平面向量与的夹角是钝角”的充分必要条件是“”
A. ①② B. ③④ C. ②③ D. ②④
6. 已知定义在上的偶函数在上单调递增,则函数的解析式不可能是
A. B.
C. D.
7. 已知函数是定义在上的奇函数,对任意的都有,当时,则
A B. C. D.
8. 已知定义在上的函数满足为偶函数,若在内单调递减,则下面结论正确的是
A. B.
C. D.
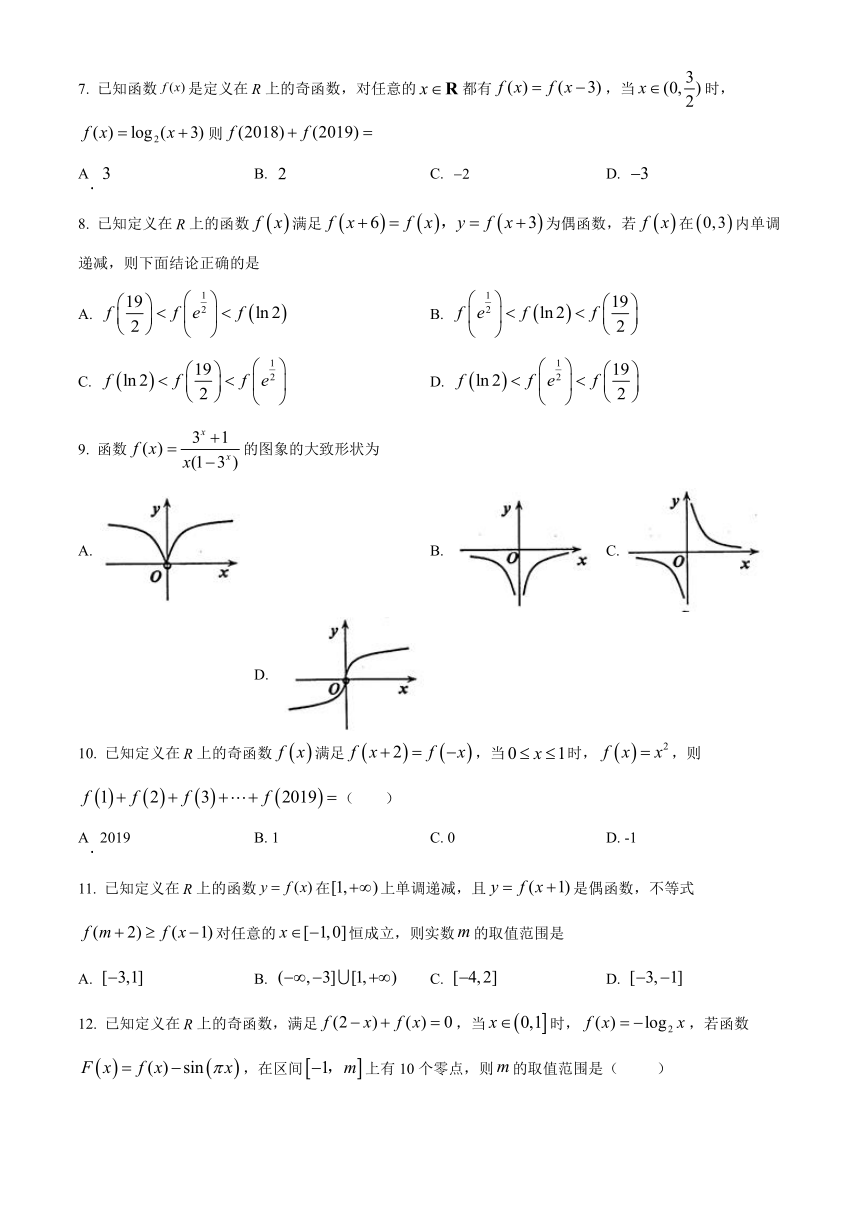
9. 函数的图象的大致形状为
A. B. C. D.
10. 已知定义在上的奇函数满足,当时,,则( )
A 2019 B. 1 C. 0 D. -1
11. 已知定义在上的函数在上单调递减,且是偶函数,不等式对任意的恒成立,则实数的取值范围是
A. B. C. D.
12. 已知定义在上的奇函数,满足,当时,,若函数,在区间上有10个零点,则的取值范围是( )
A. B. C. D.
二、填空题(本题共计4小题,每题5分,共计20分)
13. 已知函数,是定义在区间上的奇函数,则_________.
14. 已知是奇函数,且当时,.若,则__________.
15. 已知.若的值域为,则实数的取值范围是______.
16. 以下结论正确的是____________
(1)如果函数在区间上是连续不断一条曲线,并且有,那么,函数在区间内有零点;
(2)命题,则;
(3)空集是任何集合的真子集;
(4)“”是“的充分不必要条件”
(5)已知函数在定义域上是增函数,则实数取值范围是
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程)
17. 已知命题,使;命题,使.
(1)若命题为假命题,求实数的取值范围;
(2)若为真命题,为假命题,求实数的取值范围.
18. 已知分别为三个内角的对边,.
(1)求;
(2)若,的面积为,求,.
19. 在公差不为零的等差数列中,,且,,成等比数列.
(1)求的通项公式;
(2)设,求数列的前项和.
20. 函数.
(1)若,求方程的根;
(2)若对任意恒成立,求的取值范围
21. 已知函数.
(1)若函数在处的切线方程为,求的值;
(2)若函数无零点,求的取值范围.
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
选修4—4:坐标系与参数方程
22. 在直角坐标系中,圆的方程为.
(Ⅰ)以坐标原点为极点,轴正半轴为极轴建立极坐标系,求的极坐标方程;
(Ⅱ)直线的参数方程是(为参数),与交于两点,,求的斜率.
选修4—5:不等式选讲
23. 设函数(,实数).
(1)若 ,求实数的取值范围;
(2)求证:.
北外西宁新华联国际学校2022-2023学年第一学期
开学摸底考试高三数学试卷
试卷分值:150 考试时间:120分钟
一、选择题(本题共计12小题,每题5分,共计60分)
【1题答案】
【答案】A
【2题答案】
【答案】B
【3题答案】
【答案】D
【4题答案】
【答案】B
【5题答案】
【答案】C
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】A
【9题答案】
【答案】B
【10题答案】
【答案】C
【11题答案】
【答案】A
【12题答案】
【答案】A
二、填空题(本题共计4小题,每题5分,共计20分)
【13题答案】
【答案】27
【14题答案】
【答案】-3
【15题答案】
【答案】
【16题答案】
【答案】(1)(5).
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程)
【17题答案】
【答案】(1)(2)
【18题答案】
【答案】(1)
(2)
【19题答案】
【答案】(1)
(2)
【20题答案】
【答案】(1);
(2).
【21题答案】
【答案】(1)a=2;(2).
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
选修4—4:坐标系与参数方程
【22题答案】
【答案】(Ⅰ);(Ⅱ).
选修4—5:不等式选讲
【23题答案】
【答案】(1)
(2)证明见解析
开学摸底考试高三数学试卷
试卷分值:150 考试时间:120分钟
一、选择题(本题共计12小题,每题5分,共计60分)
1. 设集合,,则( )
A. B. C. D.
2. 下列函数既是奇函数又在(﹣1,1)上是减函数的是( )
A. B.
C. y=x﹣1 D. y=tanx
3. 已知两个不同的平面,和两条不同的直线,满足,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 设,,,则a,b,c的大小关系是
A. B. C. D.
5. 下列各命题中正确命题序号是
① “若都是奇数,则是偶数”的逆否命题是“不是偶数,则都不是奇数”;
② 命题“”的否定是“” ;
③ “函数的最小正周期为” 是“”的必要不充分条件;
④“平面向量与的夹角是钝角”的充分必要条件是“”
A. ①② B. ③④ C. ②③ D. ②④
6. 已知定义在上的偶函数在上单调递增,则函数的解析式不可能是
A. B.
C. D.
7. 已知函数是定义在上的奇函数,对任意的都有,当时,则
A B. C. D.
8. 已知定义在上的函数满足为偶函数,若在内单调递减,则下面结论正确的是
A. B.
C. D.
9. 函数的图象的大致形状为
A. B. C. D.
10. 已知定义在上的奇函数满足,当时,,则( )
A 2019 B. 1 C. 0 D. -1
11. 已知定义在上的函数在上单调递减,且是偶函数,不等式对任意的恒成立,则实数的取值范围是
A. B. C. D.
12. 已知定义在上的奇函数,满足,当时,,若函数,在区间上有10个零点,则的取值范围是( )
A. B. C. D.
二、填空题(本题共计4小题,每题5分,共计20分)
13. 已知函数,是定义在区间上的奇函数,则_________.
14. 已知是奇函数,且当时,.若,则__________.
15. 已知.若的值域为,则实数的取值范围是______.
16. 以下结论正确的是____________
(1)如果函数在区间上是连续不断一条曲线,并且有,那么,函数在区间内有零点;
(2)命题,则;
(3)空集是任何集合的真子集;
(4)“”是“的充分不必要条件”
(5)已知函数在定义域上是增函数,则实数取值范围是
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程)
17. 已知命题,使;命题,使.
(1)若命题为假命题,求实数的取值范围;
(2)若为真命题,为假命题,求实数的取值范围.
18. 已知分别为三个内角的对边,.
(1)求;
(2)若,的面积为,求,.
19. 在公差不为零的等差数列中,,且,,成等比数列.
(1)求的通项公式;
(2)设,求数列的前项和.
20. 函数.
(1)若,求方程的根;
(2)若对任意恒成立,求的取值范围
21. 已知函数.
(1)若函数在处的切线方程为,求的值;
(2)若函数无零点,求的取值范围.
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
选修4—4:坐标系与参数方程
22. 在直角坐标系中,圆的方程为.
(Ⅰ)以坐标原点为极点,轴正半轴为极轴建立极坐标系,求的极坐标方程;
(Ⅱ)直线的参数方程是(为参数),与交于两点,,求的斜率.
选修4—5:不等式选讲
23. 设函数(,实数).
(1)若 ,求实数的取值范围;
(2)求证:.
北外西宁新华联国际学校2022-2023学年第一学期
开学摸底考试高三数学试卷
试卷分值:150 考试时间:120分钟
一、选择题(本题共计12小题,每题5分,共计60分)
【1题答案】
【答案】A
【2题答案】
【答案】B
【3题答案】
【答案】D
【4题答案】
【答案】B
【5题答案】
【答案】C
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】A
【9题答案】
【答案】B
【10题答案】
【答案】C
【11题答案】
【答案】A
【12题答案】
【答案】A
二、填空题(本题共计4小题,每题5分,共计20分)
【13题答案】
【答案】27
【14题答案】
【答案】-3
【15题答案】
【答案】
【16题答案】
【答案】(1)(5).
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程)
【17题答案】
【答案】(1)(2)
【18题答案】
【答案】(1)
(2)
【19题答案】
【答案】(1)
(2)
【20题答案】
【答案】(1);
(2).
【21题答案】
【答案】(1)a=2;(2).
请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
选修4—4:坐标系与参数方程
【22题答案】
【答案】(Ⅰ);(Ⅱ).
选修4—5:不等式选讲
【23题答案】
【答案】(1)
(2)证明见解析
同课章节目录
