2022-2023学年人教版九年级数学下册第二十七章 相似 几何的五大模型(三)风筝模型和蝴蝶模型(含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册第二十七章 相似 几何的五大模型(三)风筝模型和蝴蝶模型(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 128.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览


文档简介
几何的五大模型之风筝模型和蝴蝶模型
☆基础题
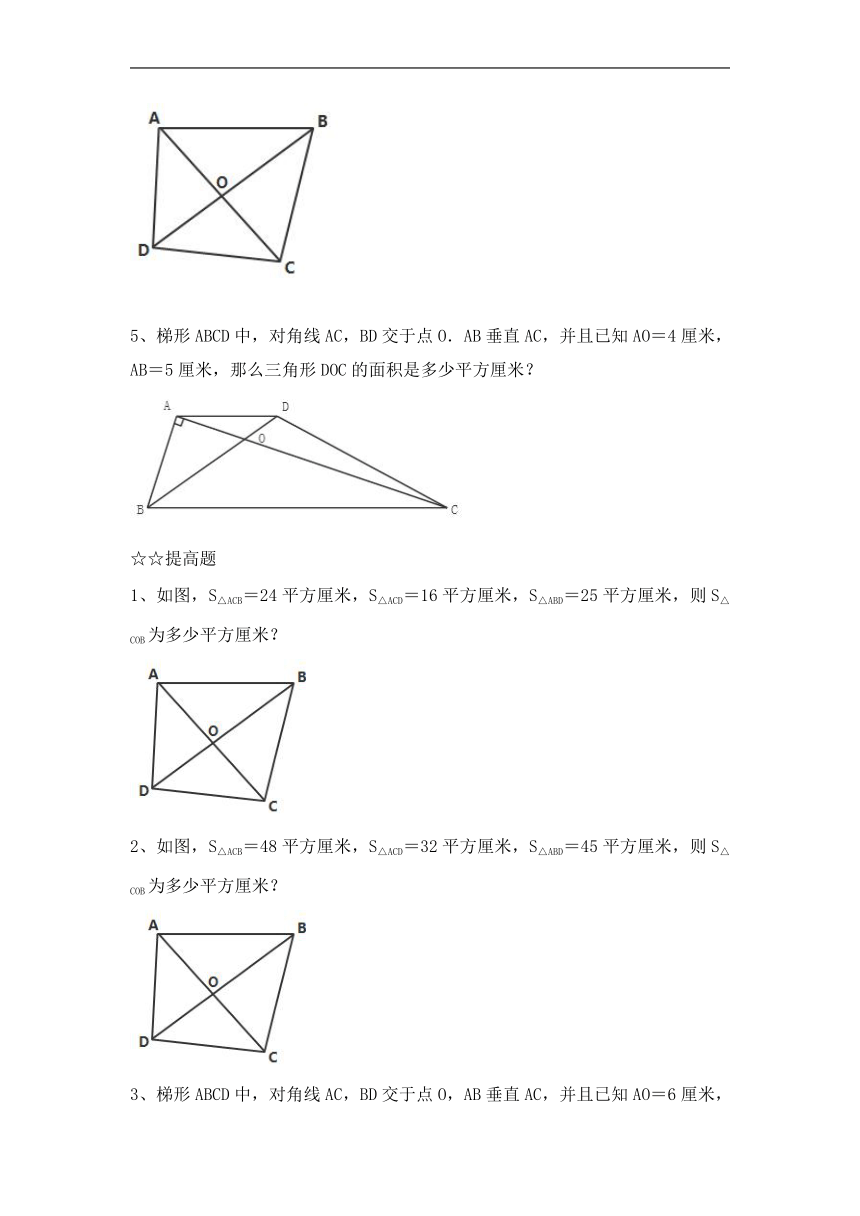
1、如图,S△AOB=24平方厘米,S△AOD=18平方厘米,S△COD=12平方厘米,则S△COB为多少平方厘米?
2、如图,S四边形ABCD=52平方厘米,S△AOB=7平方厘米,S△AOD=6平方厘米,则S△COB为多少平方厘米?
3、如图,S四边形ABCD=56平方厘米,S△AOB=8平方厘米,S△AOD=6平方厘米,则S△COB为多少平方厘米?
4、如图,S△ACB=27平方厘米,S△ACD=18平方厘米,DO=15厘米,则BO多少厘米?
5、梯形ABCD中,对角线AC,BD交于点O.AB垂直AC,并且已知AO=4厘米,AB=5厘米,那么三角形DOC的面积是多少平方厘米?
☆☆提高题
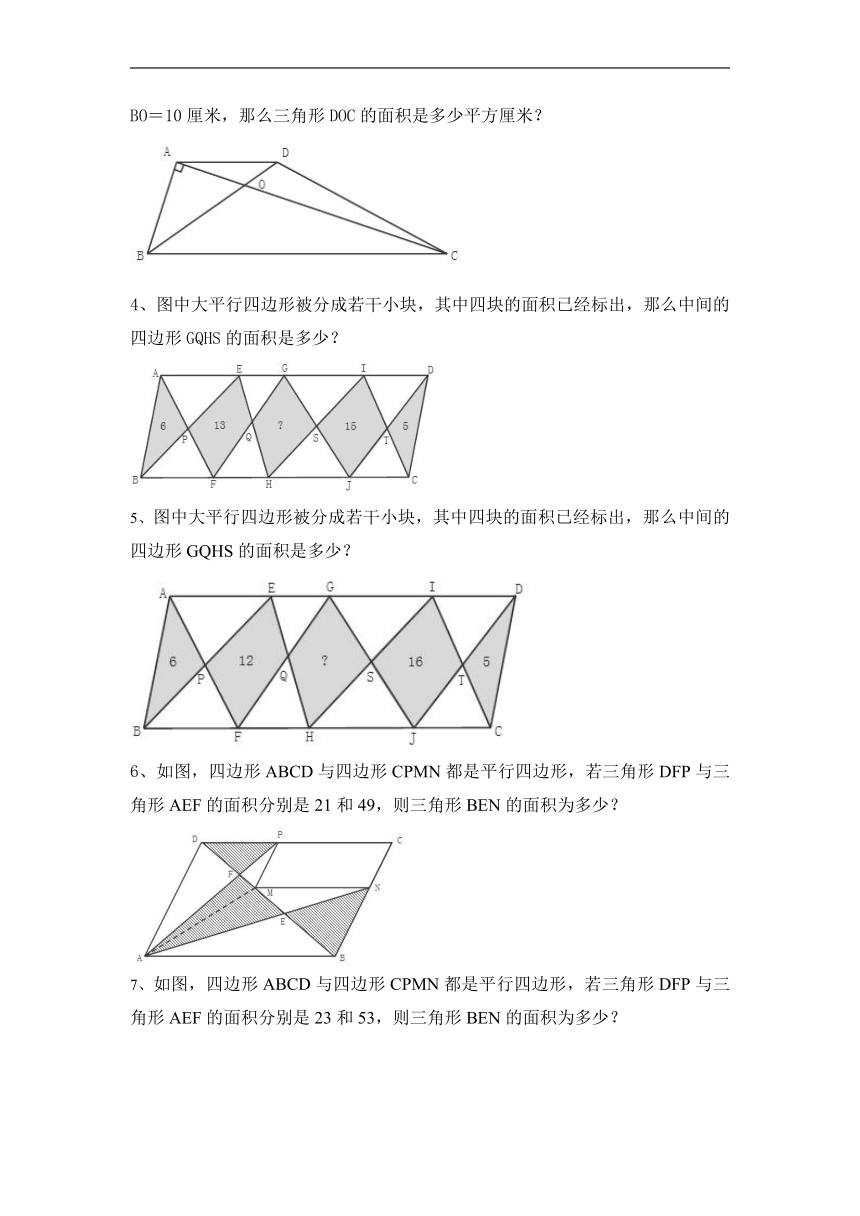
1、如图,S△ACB=24平方厘米,S△ACD=16平方厘米,S△ABD=25平方厘米,则S△COB为多少平方厘米?
2、如图,S△ACB=48平方厘米,S△ACD=32平方厘米,S△ABD=45平方厘米,则S△COB为多少平方厘米?
3、梯形ABCD中,对角线AC,BD交于点O,AB垂直AC,并且已知AO=6厘米,BO=10厘米,那么三角形DOC的面积是多少平方厘米?
4、图中大平行四边形被分成若干小块,其中四块的面积已经标出,那么中间的四边形GQHS的面积是多少?
5、图中大平行四边形被分成若干小块,其中四块的面积已经标出,那么中间的四边形GQHS的面积是多少?
6、如图,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是21和49,则三角形BEN的面积为多少?
7、如图,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是23和53,则三角形BEN的面积为多少?
☆☆☆竞赛题
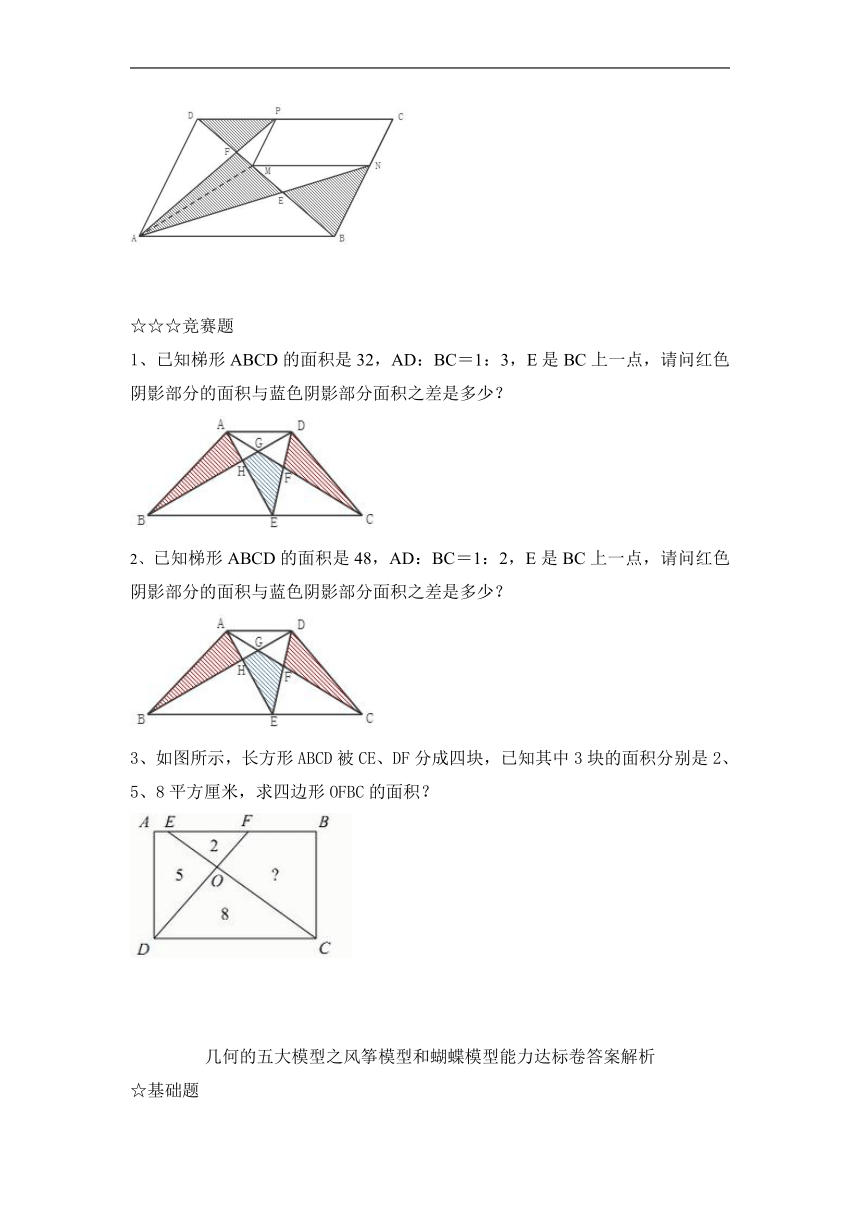
1、已知梯形ABCD的面积是32,AD:BC=1:3,E是BC上一点,请问红色阴影部分的面积与蓝色阴影部分面积之差是多少?
2、已知梯形ABCD的面积是48,AD:BC=1:2,E是BC上一点,请问红色阴影部分的面积与蓝色阴影部分面积之差是多少?
3、如图所示,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别是2、5、8平方厘米,求四边形OFBC的面积?
几何的五大模型之风筝模型和蝴蝶模型能力达标卷答案解析
☆基础题
1、答案:16平方厘米
解析:在四边形ABCD中,根据风筝模型得:S△AOD:S△AOB=S△COD:S△COB,即18:24=12:S△COB,S△COB=24×12÷18=16(平方厘米)
2、答案:21平方厘米
解析:在四边形ABCD中,根据风筝模型得:S△AOD:S△AOB=S△COD:S△COB=6:7,
S△COD+S△COB=52—(6+7)=39(平方厘米),所以S△COB=39×=21(平方厘米)
3、答案:24平方厘米
解析:在四边形ABCD中,根据风筝模型得:S△AOD:S△AOB=S△COD:S△COB=6:8=3:4,
S△COD+S△COB=56—(6+8)=42(平方厘米),所以S△COB=42×=24(平方厘米)
4、答案:22.5厘米
解析:在四边形ABCD中,根据风筝模型得:DO:BO=S△ACD:S△ACB=18:27=2:3,
所以BO=15÷2×3=22.5(厘米)
5、答案:10平方厘米
解析:在梯形ABCD中,根据蝴蝶定理得:S△DOC=S△AOB=4×5÷2=10(平方厘米)
☆☆提高题
1、答案:9平方厘米
解析:在四边形ABCD中,根据风筝模型得:DO:BO=S△ACD:S△ACB=16:24=2:3,
则:S△AOB=S△ABD=×25=15(平方厘米),则S△COB=S△ACB—S△AOB=24—15=9(平方厘米)
2、答案:21平方厘米
解析:在四边形ABCD中,根据风筝模型得:DO:BO=S△ACD:S△ACB=32:48=2:3,
则S△AOB=S△ABD=×45=27(平方厘米),则S△COB=S△ACB—S△AOB=48—27=21(平方厘米)
3、答案:24平方厘米
解析:在梯形ABCD中,根据蝴蝶定理得:S△DOC=S△AOB
在直角三角形AOB中,根据勾股定理得:AB2=OB2—OA2=102—62=64=82,所以AB=8
所以:S△DOC=S△AOB=6×8÷2=24(平方厘米)
4、答案:17
解析:如下图,连接EF、GH和IJ
在平行四边形ABEF中,根据蝴蝶模型得:S△ABP=S△EPF=6,在平行四边形EFGH中,S△EQF=S△GQH=13—6=7;在平行四边形IDCJ中,S△DCT=S△IJT=5,在平行四边形GIJH中,S△GSH=S△ISJ=15—5=10,所以S四边形GQHS=S△GQH+S△ISJ=7+10=17
5、答案:17
解析:如下图,连接EF、GH和IJ
在平行四边形ABEF中,根据蝴蝶模型得:S△ABP=S△EPF=6,在平行四边形EFGH中,S△EQF=S△GQH=12—6=6;在平行四边形IDCJ中,S△DCT=S△IJT=5,在平行四边形GIJH中,S△GSH=S△ISJ=16—5=11,所以S四边形GQHS=S△GQH+S△ISJ=6+11=17
6、答案:28
解析:如下图,连接AM。
在四边形AMPD中,因为PM∥AD,根据蝴蝶模型得:S△DFP=S△AMF=21
S△AME=S△AEF—S△DFP=49—21=28
在四边形ABNM中,因为MN∥AB,根据蝴蝶模型得:S△BENd=S△AME=28
7、答案:30
解析:如下图,连接AM。
在四边形AMPD中,因为PM∥AD,根据蝴蝶模型得:S△DFP=S△AMF=23
S△AME=S△AEF—S△DFP=53—23=30
在四边形ABNM中,因为MN∥AB,根据蝴蝶模型得:S△BENd=S△AME=30
如图,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是23和53,则三角形BEN的面积为多少?
☆☆☆竞赛题
1、答案:6
解析:在梯形ABCD中,根据蝴蝶模型得:S△ABH=S△DEH,所以S红色—S蓝色=S△CDG
在梯形ABCD中,因为AD:BC=1:3,所以S△ADG:S△ABH:S△BGC:S△CDG=1:3:9:3
又因为梯形ABCD的面积是32,所以S△CDG=32÷(1+3+9+3)×3=6
2、答案:
解析:在梯形ABCD中,根据蝴蝶模型得:S△ABH=S△DEH,所以S红色—S蓝色=S△CDG
在梯形ABCD中,因为AD:BC=1:2,所以S△ADG:S△ABH:S△BGC:S△CDG=1:2:4:2
又因为梯形ABCD的面积是48,所以S△CDG=48÷(1+2+4+2)×2=
3、答案:
解析:如下图,连接CF。
因为S△EOF:S△COD=2:8=1:4,所以,则S△FOC=2×2=4(平方厘米),S△DFC=8+4=12(平方厘米),S长方形ABCD=12×2=24(平方厘米),所以:S四边形OFBC=24—2—5—8=9(平方厘米)
☆基础题
1、如图,S△AOB=24平方厘米,S△AOD=18平方厘米,S△COD=12平方厘米,则S△COB为多少平方厘米?
2、如图,S四边形ABCD=52平方厘米,S△AOB=7平方厘米,S△AOD=6平方厘米,则S△COB为多少平方厘米?
3、如图,S四边形ABCD=56平方厘米,S△AOB=8平方厘米,S△AOD=6平方厘米,则S△COB为多少平方厘米?
4、如图,S△ACB=27平方厘米,S△ACD=18平方厘米,DO=15厘米,则BO多少厘米?
5、梯形ABCD中,对角线AC,BD交于点O.AB垂直AC,并且已知AO=4厘米,AB=5厘米,那么三角形DOC的面积是多少平方厘米?
☆☆提高题
1、如图,S△ACB=24平方厘米,S△ACD=16平方厘米,S△ABD=25平方厘米,则S△COB为多少平方厘米?
2、如图,S△ACB=48平方厘米,S△ACD=32平方厘米,S△ABD=45平方厘米,则S△COB为多少平方厘米?
3、梯形ABCD中,对角线AC,BD交于点O,AB垂直AC,并且已知AO=6厘米,BO=10厘米,那么三角形DOC的面积是多少平方厘米?
4、图中大平行四边形被分成若干小块,其中四块的面积已经标出,那么中间的四边形GQHS的面积是多少?
5、图中大平行四边形被分成若干小块,其中四块的面积已经标出,那么中间的四边形GQHS的面积是多少?
6、如图,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是21和49,则三角形BEN的面积为多少?
7、如图,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是23和53,则三角形BEN的面积为多少?
☆☆☆竞赛题
1、已知梯形ABCD的面积是32,AD:BC=1:3,E是BC上一点,请问红色阴影部分的面积与蓝色阴影部分面积之差是多少?
2、已知梯形ABCD的面积是48,AD:BC=1:2,E是BC上一点,请问红色阴影部分的面积与蓝色阴影部分面积之差是多少?
3、如图所示,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别是2、5、8平方厘米,求四边形OFBC的面积?
几何的五大模型之风筝模型和蝴蝶模型能力达标卷答案解析
☆基础题
1、答案:16平方厘米
解析:在四边形ABCD中,根据风筝模型得:S△AOD:S△AOB=S△COD:S△COB,即18:24=12:S△COB,S△COB=24×12÷18=16(平方厘米)
2、答案:21平方厘米
解析:在四边形ABCD中,根据风筝模型得:S△AOD:S△AOB=S△COD:S△COB=6:7,
S△COD+S△COB=52—(6+7)=39(平方厘米),所以S△COB=39×=21(平方厘米)
3、答案:24平方厘米
解析:在四边形ABCD中,根据风筝模型得:S△AOD:S△AOB=S△COD:S△COB=6:8=3:4,
S△COD+S△COB=56—(6+8)=42(平方厘米),所以S△COB=42×=24(平方厘米)
4、答案:22.5厘米
解析:在四边形ABCD中,根据风筝模型得:DO:BO=S△ACD:S△ACB=18:27=2:3,
所以BO=15÷2×3=22.5(厘米)
5、答案:10平方厘米
解析:在梯形ABCD中,根据蝴蝶定理得:S△DOC=S△AOB=4×5÷2=10(平方厘米)
☆☆提高题
1、答案:9平方厘米
解析:在四边形ABCD中,根据风筝模型得:DO:BO=S△ACD:S△ACB=16:24=2:3,
则:S△AOB=S△ABD=×25=15(平方厘米),则S△COB=S△ACB—S△AOB=24—15=9(平方厘米)
2、答案:21平方厘米
解析:在四边形ABCD中,根据风筝模型得:DO:BO=S△ACD:S△ACB=32:48=2:3,
则S△AOB=S△ABD=×45=27(平方厘米),则S△COB=S△ACB—S△AOB=48—27=21(平方厘米)
3、答案:24平方厘米
解析:在梯形ABCD中,根据蝴蝶定理得:S△DOC=S△AOB
在直角三角形AOB中,根据勾股定理得:AB2=OB2—OA2=102—62=64=82,所以AB=8
所以:S△DOC=S△AOB=6×8÷2=24(平方厘米)
4、答案:17
解析:如下图,连接EF、GH和IJ
在平行四边形ABEF中,根据蝴蝶模型得:S△ABP=S△EPF=6,在平行四边形EFGH中,S△EQF=S△GQH=13—6=7;在平行四边形IDCJ中,S△DCT=S△IJT=5,在平行四边形GIJH中,S△GSH=S△ISJ=15—5=10,所以S四边形GQHS=S△GQH+S△ISJ=7+10=17
5、答案:17
解析:如下图,连接EF、GH和IJ
在平行四边形ABEF中,根据蝴蝶模型得:S△ABP=S△EPF=6,在平行四边形EFGH中,S△EQF=S△GQH=12—6=6;在平行四边形IDCJ中,S△DCT=S△IJT=5,在平行四边形GIJH中,S△GSH=S△ISJ=16—5=11,所以S四边形GQHS=S△GQH+S△ISJ=6+11=17
6、答案:28
解析:如下图,连接AM。
在四边形AMPD中,因为PM∥AD,根据蝴蝶模型得:S△DFP=S△AMF=21
S△AME=S△AEF—S△DFP=49—21=28
在四边形ABNM中,因为MN∥AB,根据蝴蝶模型得:S△BENd=S△AME=28
7、答案:30
解析:如下图,连接AM。
在四边形AMPD中,因为PM∥AD,根据蝴蝶模型得:S△DFP=S△AMF=23
S△AME=S△AEF—S△DFP=53—23=30
在四边形ABNM中,因为MN∥AB,根据蝴蝶模型得:S△BENd=S△AME=30
如图,四边形ABCD与四边形CPMN都是平行四边形,若三角形DFP与三角形AEF的面积分别是23和53,则三角形BEN的面积为多少?
☆☆☆竞赛题
1、答案:6
解析:在梯形ABCD中,根据蝴蝶模型得:S△ABH=S△DEH,所以S红色—S蓝色=S△CDG
在梯形ABCD中,因为AD:BC=1:3,所以S△ADG:S△ABH:S△BGC:S△CDG=1:3:9:3
又因为梯形ABCD的面积是32,所以S△CDG=32÷(1+3+9+3)×3=6
2、答案:
解析:在梯形ABCD中,根据蝴蝶模型得:S△ABH=S△DEH,所以S红色—S蓝色=S△CDG
在梯形ABCD中,因为AD:BC=1:2,所以S△ADG:S△ABH:S△BGC:S△CDG=1:2:4:2
又因为梯形ABCD的面积是48,所以S△CDG=48÷(1+2+4+2)×2=
3、答案:
解析:如下图,连接CF。
因为S△EOF:S△COD=2:8=1:4,所以,则S△FOC=2×2=4(平方厘米),S△DFC=8+4=12(平方厘米),S长方形ABCD=12×2=24(平方厘米),所以:S四边形OFBC=24—2—5—8=9(平方厘米)
