2022-2023学年人教版九年级数学下册第二十七章 相似 几何的五大模型(四)燕尾模型(含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册第二十七章 相似 几何的五大模型(四)燕尾模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 368.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 18:41:09 | ||
图片预览

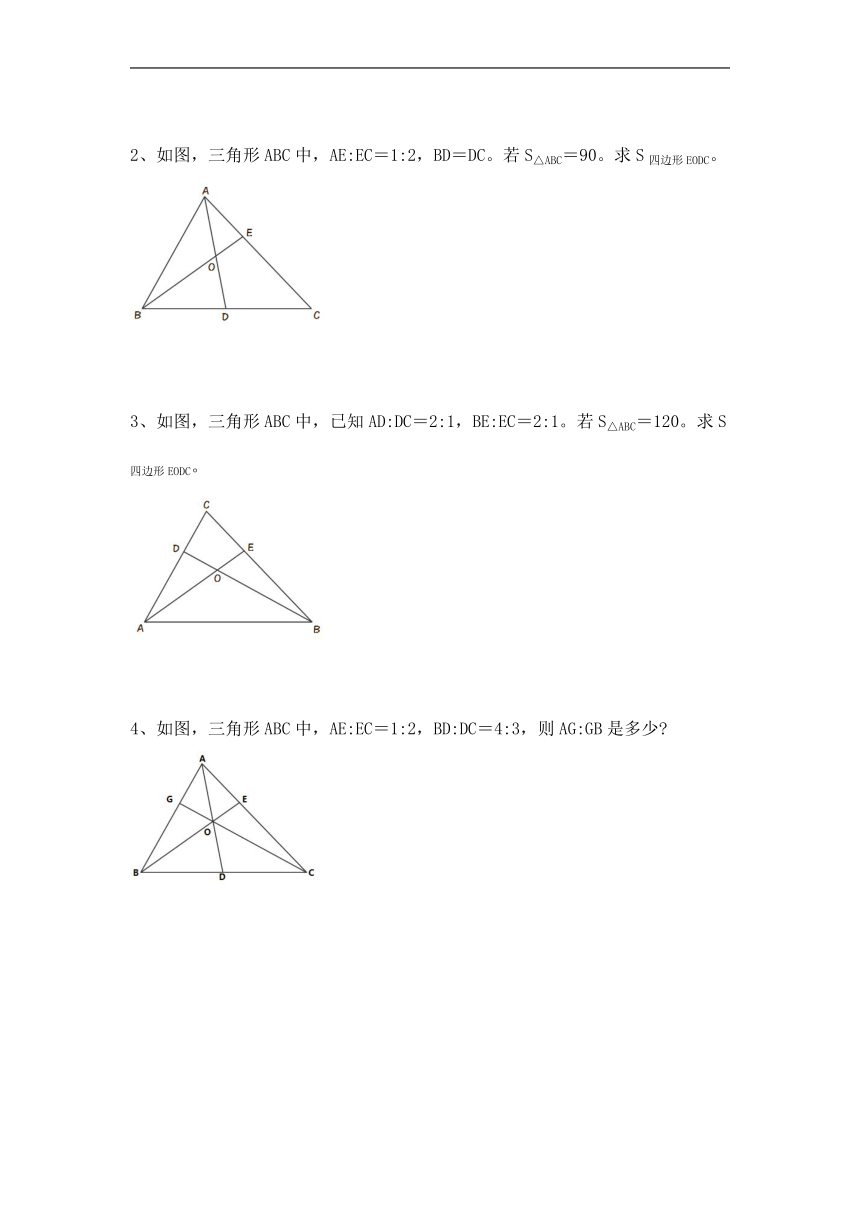

文档简介
几何的五大模型之燕尾模型
☆基础题
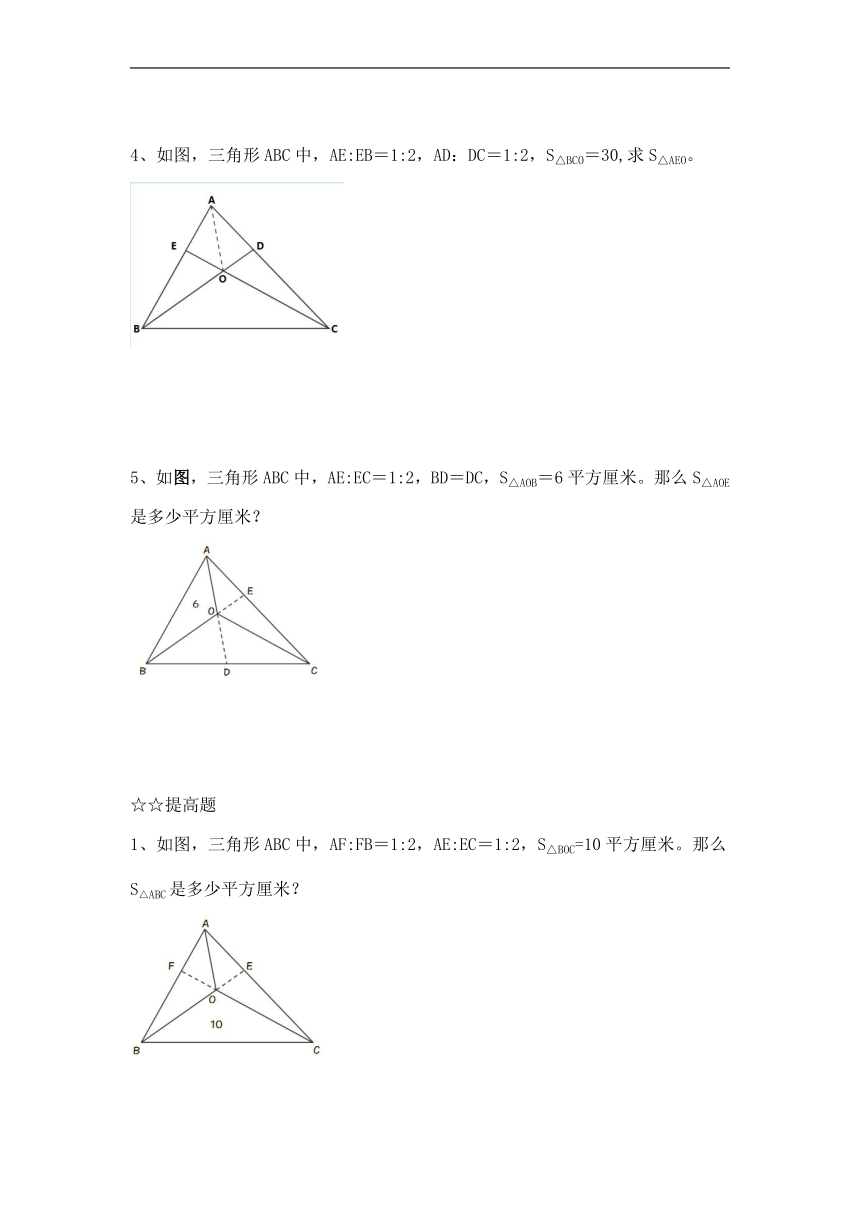
1、如图,三角形ABC中,AD:DC=2:3,S△ABO=12,求S△BCO。
2、三角形ABC中,AB=49,S△AOC=20,S△BCO=50,求AD的长。
3、如图,三角形ABC中,AE:EC=1:2,BD=DC,S△ABO=18,求S△BDO。
4、如图,三角形ABC中,AE:EB=1:2,AD:DC=1:2,S△BCO=30,求S△AEO。
5、如图,三角形ABC中,AE:EC=1:2,BD=DC,S△AOB=6平方厘米。那么S△AOE是多少平方厘米?
☆☆提高题
1、如图,三角形ABC中,AF:FB=1:2,AE:EC=1:2,S△BOC=10平方厘米。那么S△ABC是多少平方厘米?
2、如图,三角形ABC中,AE:EC=1:2,BD=DC。若S△ABC=90。求S四边形EODC。
3、如图,三角形ABC中,已知AD:DC=2:1,BE:EC=2:1。若S△ABC=120。求S四边形EODC。
4、如图,三角形ABC中,AE:EC=1:2,BD:DC=4:3,则AG:GB是多少
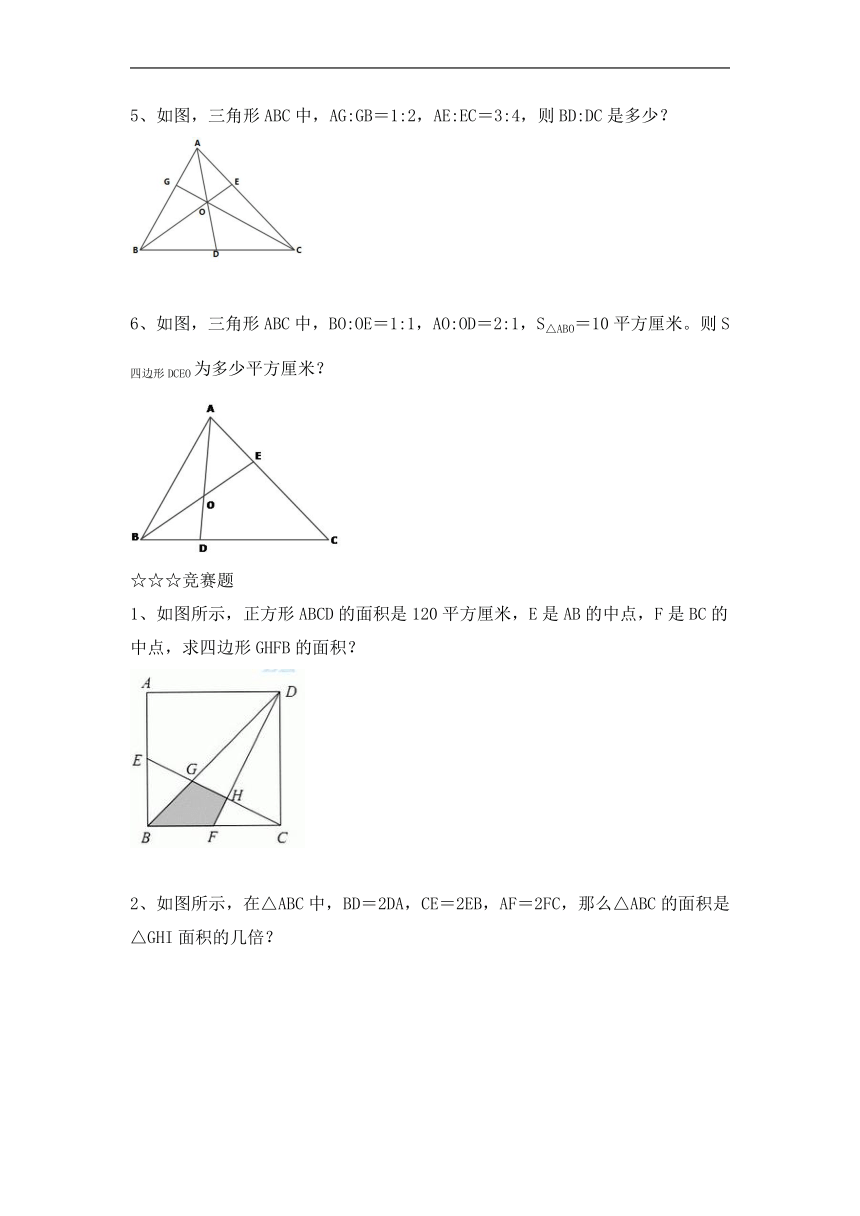
5、如图,三角形ABC中,AG:GB=1:2,AE:EC=3:4,则BD:DC是多少?
6、如图,三角形ABC中,BO:OE=1:1,AO:OD=2:1,S△ABO=10平方厘米。则S四边形DCEO为多少平方厘米?
☆☆☆竞赛题
1、如图所示,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,求四边形GHFB的面积?
2、如图所示,在△ABC中,BD=2DA,CE=2EB,AF=2FC,那么△ABC的面积是△GHI面积的几倍?
几何的五大模型之燕尾模型能力达标卷答案解析
☆基础题
1、答案:18
解析:在三角形ABC中,根据燕尾模型得:S△ABO:S△BCO=AD:DC=2:3,
所以S△BCO=12÷2×3=18
2、答案:14
解析:在三角形ABC中,根据燕尾模型得:AD:DC=S△AOC:S△BCO=20:50=2:5,
所以AD=49×=14
三角形ABC中,AB=49,S△AOC=20,S△BCO=50,求AD的长。
3、答案:18
解析:如下图,连接OC,在三角形ABC中,根据燕尾模型得:AE:EC=1:2=S△ABO:S△BOC
所以S△BOC=18×2=36,又因为BD=DC,所以S△BDO=36×=18
4、答案:5
解析:如下图,连接OA,在三角形ABC中,根据燕尾模型得:AD:DC=S△ABO:S△BCO=1:2
所以S△ABO=30÷2=15,又因为AE:EB=1:2,所以S△AEO=15×=5
5、答案:2平方厘米
解析:如下图,连接OE和OD,在三角形ABC中,根据燕尾模型得:BD:DC=S△AOB:S△ACO=1:1
所以S△ABO=S△ACO=6,又因为AE:EC=1:2,所以S△AOE=6×=2(平方厘米)
☆☆提高题
1、答案:20平方厘米
解析:如下图,连接OE和OF,在三角形ABC中,根据燕尾模型得:AE:EC=S△AOB:S△BOC=1:2
所以S△AOB=10÷2=5(平方厘米),同理可得:S△AOC=10÷2=5(平方厘米)
S△ABC=S△BOC+S△AOB+S△AOC=10+5+5=20(平方厘米)
2、答案:37.5
解析:如下图,连接OC,在三角形ABC中,根据燕尾模型得:BD:DC=S△AOB:S△ACO=1:1
所以S△AOB=S△ACO,同理AE:EC=S△AOB:S△BOC=1:2,所以S△BOC=2S△AOB,又因为S△ABC=90,S△AOB=S△ACO=90÷4=22.5,S四边形EODC=S△DCO+S△ECO=22.5+22.5×=37.5
3、答案:20
解析:如下图,连接OC,在三角形ABC中,根据燕尾模型得:AD:DC=S△AOB:S△BCO=2:1
S△AOB=2S△BCO,同理:BE:EC=S△AOB:S△ACO=2:1,S△AOB=2S△ACO
又因为S△ABC=120,所以S△BCO=S△ACO=120÷4=30,则S△CDO=S△CEO=30×=10
所以S四边形EODC=S△CDO+S△CEO=10+10=20
4、答案:3:8
解析:在三角形ABC中,根据燕尾模型得:AE:EC=S△AOB:S△BCO=1:2,S△BCO=2S△AOB
同理:BD:DC=S△AOB:S△AOC=4:3,S△AOC=S△AOB
同理:AG:GB=S△AOC:S△BCO=S△AOB:2S△AOB=:2=3:8
5、答案:3:2
解析:在三角形ABC中,根据燕尾模型得:AE:EC=S△AOB:S△BCO=3:4,S△AOB=S△BCO
同理:AG:GB=S△AOC:S△BCO=1:2,S△AOC=S△BCO
同理:BD:DC=S△AOB:S△AOC= S△BCO:S△BCO=:=3:2
6、答案:35平方厘米
解析:如下图,连接OC。
在三角形ABC中,根据题意知:S△AOB=S△AOC=10平方厘米,S△BOD=5平方厘米
设S△EOC=x,S△DOC=y,则有,解这个方程得:
S四边形DCEO=+=20+15=35(平方厘米)
☆☆☆竞赛题
1、答案:14平方厘米
解析:如下图,连接BH
因为AB∥CD,且E是AB的中点,根据沙漏模型得:
在三角形BCD中,根据燕尾模型得:BG:GD=S△BHC:S△DHC=1:2,所以S△DHC=2S△BHC
同理:BF:FC=S△BHD:S△DHC=1:1,所以S△BHD=S△DHC
S△BHC=120÷2÷(2+2+1)=12(平方厘米),S△BHD=12×2=24(平方厘米)
S四边形GHFB=S△BFH+S△BGH=S△BHC+S△BHD=12×+24×=14(平方厘米)
2、答案:7
解析:如下图,连接AI。
在三角形ABC中,根据燕尾模型得:AD:DB=S△ACI:S△BCI=1:2;
同理:AF:FC=S△ABI:S△BCI=2:1,所以S△ACI:S△BCI:S△ABI=1:2:4
S△BCI=S△ABC,同理:S△ACG=S△ABC,S△ABH=S△ABC
所以S△GHI=(1—×3)S△ABC=S△ABC,即S△ABC是S△GHI的7倍。
☆基础题
1、如图,三角形ABC中,AD:DC=2:3,S△ABO=12,求S△BCO。
2、三角形ABC中,AB=49,S△AOC=20,S△BCO=50,求AD的长。
3、如图,三角形ABC中,AE:EC=1:2,BD=DC,S△ABO=18,求S△BDO。
4、如图,三角形ABC中,AE:EB=1:2,AD:DC=1:2,S△BCO=30,求S△AEO。
5、如图,三角形ABC中,AE:EC=1:2,BD=DC,S△AOB=6平方厘米。那么S△AOE是多少平方厘米?
☆☆提高题
1、如图,三角形ABC中,AF:FB=1:2,AE:EC=1:2,S△BOC=10平方厘米。那么S△ABC是多少平方厘米?
2、如图,三角形ABC中,AE:EC=1:2,BD=DC。若S△ABC=90。求S四边形EODC。
3、如图,三角形ABC中,已知AD:DC=2:1,BE:EC=2:1。若S△ABC=120。求S四边形EODC。
4、如图,三角形ABC中,AE:EC=1:2,BD:DC=4:3,则AG:GB是多少
5、如图,三角形ABC中,AG:GB=1:2,AE:EC=3:4,则BD:DC是多少?
6、如图,三角形ABC中,BO:OE=1:1,AO:OD=2:1,S△ABO=10平方厘米。则S四边形DCEO为多少平方厘米?
☆☆☆竞赛题
1、如图所示,正方形ABCD的面积是120平方厘米,E是AB的中点,F是BC的中点,求四边形GHFB的面积?
2、如图所示,在△ABC中,BD=2DA,CE=2EB,AF=2FC,那么△ABC的面积是△GHI面积的几倍?
几何的五大模型之燕尾模型能力达标卷答案解析
☆基础题
1、答案:18
解析:在三角形ABC中,根据燕尾模型得:S△ABO:S△BCO=AD:DC=2:3,
所以S△BCO=12÷2×3=18
2、答案:14
解析:在三角形ABC中,根据燕尾模型得:AD:DC=S△AOC:S△BCO=20:50=2:5,
所以AD=49×=14
三角形ABC中,AB=49,S△AOC=20,S△BCO=50,求AD的长。
3、答案:18
解析:如下图,连接OC,在三角形ABC中,根据燕尾模型得:AE:EC=1:2=S△ABO:S△BOC
所以S△BOC=18×2=36,又因为BD=DC,所以S△BDO=36×=18
4、答案:5
解析:如下图,连接OA,在三角形ABC中,根据燕尾模型得:AD:DC=S△ABO:S△BCO=1:2
所以S△ABO=30÷2=15,又因为AE:EB=1:2,所以S△AEO=15×=5
5、答案:2平方厘米
解析:如下图,连接OE和OD,在三角形ABC中,根据燕尾模型得:BD:DC=S△AOB:S△ACO=1:1
所以S△ABO=S△ACO=6,又因为AE:EC=1:2,所以S△AOE=6×=2(平方厘米)
☆☆提高题
1、答案:20平方厘米
解析:如下图,连接OE和OF,在三角形ABC中,根据燕尾模型得:AE:EC=S△AOB:S△BOC=1:2
所以S△AOB=10÷2=5(平方厘米),同理可得:S△AOC=10÷2=5(平方厘米)
S△ABC=S△BOC+S△AOB+S△AOC=10+5+5=20(平方厘米)
2、答案:37.5
解析:如下图,连接OC,在三角形ABC中,根据燕尾模型得:BD:DC=S△AOB:S△ACO=1:1
所以S△AOB=S△ACO,同理AE:EC=S△AOB:S△BOC=1:2,所以S△BOC=2S△AOB,又因为S△ABC=90,S△AOB=S△ACO=90÷4=22.5,S四边形EODC=S△DCO+S△ECO=22.5+22.5×=37.5
3、答案:20
解析:如下图,连接OC,在三角形ABC中,根据燕尾模型得:AD:DC=S△AOB:S△BCO=2:1
S△AOB=2S△BCO,同理:BE:EC=S△AOB:S△ACO=2:1,S△AOB=2S△ACO
又因为S△ABC=120,所以S△BCO=S△ACO=120÷4=30,则S△CDO=S△CEO=30×=10
所以S四边形EODC=S△CDO+S△CEO=10+10=20
4、答案:3:8
解析:在三角形ABC中,根据燕尾模型得:AE:EC=S△AOB:S△BCO=1:2,S△BCO=2S△AOB
同理:BD:DC=S△AOB:S△AOC=4:3,S△AOC=S△AOB
同理:AG:GB=S△AOC:S△BCO=S△AOB:2S△AOB=:2=3:8
5、答案:3:2
解析:在三角形ABC中,根据燕尾模型得:AE:EC=S△AOB:S△BCO=3:4,S△AOB=S△BCO
同理:AG:GB=S△AOC:S△BCO=1:2,S△AOC=S△BCO
同理:BD:DC=S△AOB:S△AOC= S△BCO:S△BCO=:=3:2
6、答案:35平方厘米
解析:如下图,连接OC。
在三角形ABC中,根据题意知:S△AOB=S△AOC=10平方厘米,S△BOD=5平方厘米
设S△EOC=x,S△DOC=y,则有,解这个方程得:
S四边形DCEO=+=20+15=35(平方厘米)
☆☆☆竞赛题
1、答案:14平方厘米
解析:如下图,连接BH
因为AB∥CD,且E是AB的中点,根据沙漏模型得:
在三角形BCD中,根据燕尾模型得:BG:GD=S△BHC:S△DHC=1:2,所以S△DHC=2S△BHC
同理:BF:FC=S△BHD:S△DHC=1:1,所以S△BHD=S△DHC
S△BHC=120÷2÷(2+2+1)=12(平方厘米),S△BHD=12×2=24(平方厘米)
S四边形GHFB=S△BFH+S△BGH=S△BHC+S△BHD=12×+24×=14(平方厘米)
2、答案:7
解析:如下图,连接AI。
在三角形ABC中,根据燕尾模型得:AD:DB=S△ACI:S△BCI=1:2;
同理:AF:FC=S△ABI:S△BCI=2:1,所以S△ACI:S△BCI:S△ABI=1:2:4
S△BCI=S△ABC,同理:S△ACG=S△ABC,S△ABH=S△ABC
所以S△GHI=(1—×3)S△ABC=S△ABC,即S△ABC是S△GHI的7倍。
