2022-2023学年苏科版九年级数学上册《2.4 圆周角》 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年苏科版九年级数学上册《2.4 圆周角》 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 507.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 18:00:58 | ||
图片预览




文档简介
2022-2023学年苏科版九年级数学上册《2.4圆周角》同步练习题(附答案)
一.选择题
1.如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
A.60° B.50° C.45° D.40°
2.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( )
A.1:2:3:4 B.4:2:3:1 C.4:3:1:2 D.4:1:3:2
3.下列语句中,正确的是( )
A.长度相等的两条弧是等弧 B.相等的圆周角所对的弧相等
C.相等的弧所对的圆心角相等 D.平分弦的直径垂直于弦
4.如图,已知⊙O的弦AB、DC的延长线相交于点E,∠AOD=128°,∠E=40°,则∠BDC的度数是( )
A.16° B.20° C.24° D.32°
5.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,若∠C=124°,则∠B的度数为( )
A.56° B.68° C.72° D.78°
6.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=30°,半径为2,则弦CD的长为( )
A.2 B.﹣1 C. D.4
7.如图,在以AB为直径的⊙O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21° C.22.5° D.30°
8.如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且=,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
9.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
10.如图,将⊙O上的沿弦BC翻折交半径OA于点D,再将沿BD翻折交BC于点E,连接DE.若AD=2OD,则的值为( )
A. B. C. D.
11.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为( )
A.(0,5) B.(0,5) C.(0,) D.(0,)
12.在半径为3cm的⊙O中,若弦AB=3cm,则弦AB所对的圆周角的度数为( )
A.30° B.45° C.30°或150° D.45°或135°
二.填空题
13.如图,AB为⊙O的直径,点C、D在⊙O上,若∠CBA=70°,则∠D的度数是 .
14.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= .
15.如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长相交于点F.若∠A=50°,∠E=45°,则∠DCB= ,∠F= .
16.如图,直线l与⊙O相交于点B、D,点A、C是直线l两侧的圆弧上的动点,若⊙O的半径为1,∠A=30°,那么四边形ABCD的面积的最大值是 .
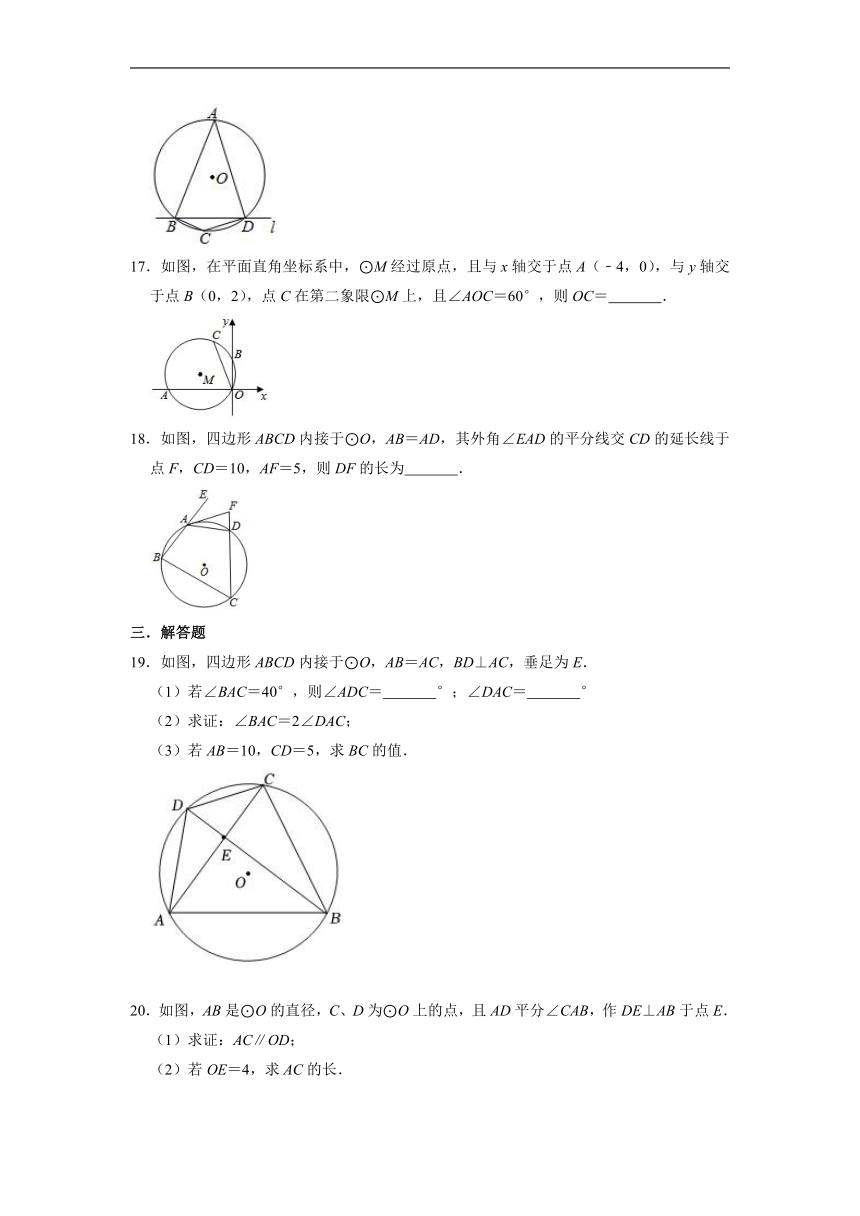
17.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(﹣4,0),与y轴交于点B(0,2),点C在第二象限⊙M上,且∠AOC=60°,则OC= .
18.如图,四边形ABCD内接于⊙O,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,则DF的长为 .
三.解答题
19.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC= °;∠DAC= °
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
20.如图,AB是⊙O的直径,C、D为⊙O上的点,且AD平分∠CAB,作DE⊥AB于点E.
(1)求证:AC∥OD;
(2)若OE=4,求AC的长.
21.如图,以P(0,3)为圆心,6为半径的⊙P交x轴于点A、B,交y轴于点C、D,连接BP并延长交⊙P于点E,连接DE交x轴于点F.
(1)求∠CDE的度数;
(2)求△BEF的面积.
22.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,连接MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
24.如图1,在Rt△ABC中,∠B=90°,∠C=40°,以AB为直径画⊙O交AC于点D,E是线段AB上的动点,延长DE交⊙O于F点,连接AF.
(1)如图1,求∠F的度数;
(2)如图2,当AE=AD时,求∠DFO的度数.
25.如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连接BD,设AP=m.
(1)求证:∠BDP=90°.
(2)若m=4,求BE的长.
(3)在点P的整个运动过程中,当AF=3CF时,求出所有符合条件的m的值.
参考答案
一.选择题
1.解:∵∠C=40°,
∴∠AOB=80°,
∵OA=OB,
∴∠OAB=∠OBA=50°.
故选:B.
2.解:∵圆的内接四边形对角互补,
∴∠A+∠C=∠B+∠D=180°,
∴∠A:∠B:∠C:∠D的可能的值是4:3:1:2.
故选:C.
3.解:A、长度相等的两条弧不一定为等弧,所以A选项错误;
B、在同圆或等圆中,相等的圆周角所对的弧相等,所以B选项错误;
C、相等的弧所对的圆心角相等,所以C选项正确;
D、平分弦(非直径)的直径垂直于弦,所以D选项错误.
故选:C.
4.解:∵∠ABD是所对的圆周角,
∴∠ABD=∠AOD=×128°=64°,
∵∠ABD是△BDE的外角,
∴∠BDC=∠ABD﹣∠E=64°﹣40°=24°,
故选:C.
5.解:∵∠C=124°,
∴∠A=180°﹣124°=56°,
∴∠BOD=2∠A=112°,
∵OD∥BC,
∴∠CDO=180°﹣124°=56°,
∴∠B=360°﹣124°﹣56°﹣112°=68°.
故选:B.
6.解:∵∠BOC=2∠A,∠A=30°,
∴∠BOC=60°,
∵AB是⊙O的直径,AB⊥CD,
∴CE=DE=CD,∠OCE=30°,
∵半径OC=2,
∴OE=OC=1,
∴CE===,
∴CD=2CE=2.
故选:C.
7.解:∵AB是直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵=3,
∴∠CAB=3∠ABC,
∴∠ABC=22.5°,∠CAB=67.5°,
∵CD⊥AB,
∴∠ACE=22.5°,
∵点H是AG的中点,∠ACB=90°,
∴AH=CH=HG,
∴∠CAH=∠ACE=22.5°,
∵∠CAF=∠CBF,
∴∠CBF=22.5°,
故选:C.
8.解:解法一、连接OD,
∵=,
∴∠DOC=∠EOC,
∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∴∠DOC=2∠B=72°,
∴∠EOC=∠DOC=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
解法二、∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∵=,
∴∠COE=2∠B=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
故选:B.
9.解:连接PA,PB,PC,过P作PD⊥AB于D,PE⊥OC于E,
∵∠ACB=60°,
∴∠APB=120°,
∵PA=PB,
∴∠PAB=∠PBA=30°,
∵A(﹣5,0),B(1,0),
∴AB=6,
∴AD=BD=3,
∴PD=,PA=PB=PC=2,
∵PD⊥AB,PE⊥OC,∠AOC=90°,
∴四边形PEOD是矩形,
∴OE=PD=,PE=OD=2,
∴CE===2,
∴OC=CE+OE=2+,
∴点C的纵坐标为2+,
故选:B.
10.解:如图,连接AC,CD,OC,过点C作CH⊥AB于H.设OA=3a,则AB=6a.
∵在同圆或等圆中,∠ABC所对的弧有,,,
∴AC=CD=DE,
∵CH⊥AD,
∴AH=DH,
∵AD=2OD,
∴AH=DH=OD=a,
在Rt△OCH中,CH===a,
在Rt△ACH中,AC===a,
∴===,
故选:D.
11.解:连接CA,OA,
∵∠OBC=30°,
∴∠CAO=60°,
又∵CA=AO,
∴△CAO是等边三角形,
∴CO=AO=5,
∴点C的坐标为:(0,5).
故选:A.
12.解:如图所示,
连接OA,OB,
则OA=OB=3cm,
∵AB=3cm,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴劣弧AB的度数是90°,优弧AB的度数是360°﹣90°=270°,
∴弦AB对的圆周角的度数是45°或135°,
故选:D.
二.填空题
13.解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CBA=70°,
∴∠A=20°,
∴∠D=∠A=20°.
故答案为20°.
14.解:连接OD,
∵AD∥OC,
∴∠DAB=∠BOC=50°,
∵OA=OD
∴∠AOD=180°﹣2∠DAB=80°,
∴∠ACD=∠AOD=40°
故答案为40°
15.解:∵四边形ABCD内接于⊙O,
∴∠A+∠DCB=180°,
∵∠A=50°,
∴∠DCB=180°﹣50°=130°,
∵∠CBF是△ABE的外角,∠A=50°,∠E=45°,
∴∠CBF=∠A+∠E=95°,
∴∠F=∠DCB﹣∠CBF=35°,
故答案为:130°;35°.
16.解:当A点和C点到BD的距离最大时,四边形ABCD的面积最大,此时A点和C点为BD所对弧的中点,
∴AC为⊙O的直径,如图,
∴AC⊥BD,
∵∠BAC=30°,
∴∠BOC=30°,
在Rt△OBH中,BH=OB=,
∴S△ABC= BH AC=×2×=,
∴四边形ABCD的面积=2×=1,
∴四边形ABCD的面积的最大值为1.
故答案为1.
17.解:连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.
∵∠AOB=90°,
∴AB是直径,
∵A(﹣4,0),B(0,2),
∴AB===2,
∵∠AMC=2∠AOC=120°,
∴AC=AM=,
在Rt△COH中,OH=a,CH=OH=a,
∴AH=4﹣a,
在Rt△ACH中,AC2=AH2+CH2,
∴15=(4﹣a)2+(a)2,
∴a=2+或2﹣(因为OC>OB,所以2﹣舍弃),
∴OC=2+.
故答案为:2+.
18.解:连接AC,
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
又∠BAD+∠EAD=180°,
∴∠EAD=∠BCD,
∵AB=AD,
∴=,
∴∠ACB=∠ACD=BCD,
∵AF平分∠EAD,
∴∠FAD=∠EAD,
∴∠FCA=∠FAD,
又∠AFC=∠DFA,
∴DF=5﹣5,
故答案为:5﹣5.
三.解答题
19.(1)解:∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°,
∴∠ADC=180°﹣∠ABC=180°﹣70°=110°;
∵AC⊥BD,
∴∠CBD=90°﹣∠ACB=20°,
∴∠DAC=∠DBC=20°;
故答案为:110,20;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=∠CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
∴,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
20.(1)证明:∵AD平分∠CAB,
∴∠OAC=2∠OAD.
∵∠BOD=2∠BAD,
∴∠BOD=∠OAC,
∴AC∥OD.
(2)解:作OF⊥AC于点F,如图所示:
则AF=AC,
∵AC∥OD,
∴∠DOE=∠OAF.
在△DOE和△OAF中,,
∴△DOE≌△OAF(AAS),
∴OE=AF=AC,
∴AC=2OE=8.
21.解:(1)∵P(0,3),
∴OP=3,
∵⊙P的半径是6,
∴PB=6,
∴OP=PB,
∵x轴⊥y轴,
∴∠POB=90°,
∴∠PBO=30°,
∴∠BPO=90°﹣30°=60°,
∵PE=PD,∠E+∠CDE=∠BPO,
∴∠CDE=∠E=60°=30°;
(2)连接PF,
∵∠PBO=∠E=30°,
∴BF=EF,
∵PE=PB=6,
∴PF⊥BE,
即∠EPF=90°,
∴EF=2PF,
由勾股定理得:PE2+PF2=EF2,
即62+PF2=(2PF)2,
解得:PF=2,
EF=BF=4,
∴△BEF的面积是==12.
22.(1)证明:连接AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE;
(2)连接DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴BA=9,
∴AC=BA=9.
23.解:(1)设⊙O的半径长为r,
则OD=r,OE=r﹣8,
∵AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,
∴DE=12,
∴OD2=OE2+DE2,
即r2=(r﹣8)2+122,
解得,r=13,
即⊙O的半径是13;
(2)连接BC,
∵∠DMB=∠D,∠DMB=∠DCB,
∴∠D=∠DCB,
∵AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,
∴CE=DE=12,∠CEB=∠DEO,
∴△CEB≌△DEO(ASA),
∴OE=BE=0.5OB,
设⊙O的半径长为r,
则r2=122+(0.5r)2,
解得,r=或r=﹣8(舍去),
∴OE=4.
24.解:(1)如图1,连接OD,
在Rt△ABC中,∠B=90°,∠C=40°,
∴∠BAC=50°,
∵OA=OD,
∴∠ODA=∠OAD=50°,
∴∠AOD=180°﹣50°﹣50°=80°,
∴∠F=∠AOD=40°;
(2)如图2,连接OD,
在Rt△ABC中,∠B=90°,∠C=40°,
∴∠BAC=50°,
∵OA=OD,
∴∠ODA=∠OAD=50°,
∵AE=AD,
∴∠ADE=∠AED=(180°﹣50°)=65°,
∴∠ODF=∠ADE﹣∠ODA=65°﹣50°=15°,
∵OF=OD,
∴∠DFO=∠FDO=15°.
25.解:(1)如图1,∵PA=PC=PD,
∴∠PDC=∠PCD,
∵CD∥BP,
∴∠BPA=∠PCD、∠BPD=∠PDC,
∴∠BPA=∠BPD,
∵BP=BP,
∴△BAP≌△BDP(SAS),
∴∠BDP=∠BAP=90°.
(2)∵∠BAO=90°,BE∥AO,
∴∠ABE=∠BAO=90°,
∵EF⊥AO,
∴∠EFA=90°,
∴四边形ABEF是矩形,
设BE=AF=x,则PF=x﹣4,
∵∠BDP=90°,
∴∠BDE=90°=∠PFE,
∵BE∥AO,
∴∠BED=∠EPF,
∵△BAP≌△BDP,
∴BD=BA=EF=8,
∴△BDE≌△EFP,
∴PE=BE=x,
在Rt△PFE中,PF2+FE2=PE2,即(x﹣4)2+82=x2,
解得:x=10,
∴BE的长为10.
(3)如图1,当点C在AF的左侧时,
∵AF=3CF,则AC=2CF,
∴CF=AP=PC=m,
∴PF=2m,PE=BE=AF=3m,
在Rt△PEF中,由PF2+EF2=PE2可得(2m)2+82=(3m)2,
解得:m=(负值舍去);
如图2,当点C在AF的右侧时,
∵AF=3CF,
∴AC=4CF,
∴CF=AP=PC=m,
∴PF=m﹣m=m,PE=BE=AF=m+m=m,
在Rt△PEF中,由PF2+EF2=PE2可得(m)2+82=(m)2,
解得:m=4(负值舍去);
综上,m的值为或4.
一.选择题
1.如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
A.60° B.50° C.45° D.40°
2.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是( )
A.1:2:3:4 B.4:2:3:1 C.4:3:1:2 D.4:1:3:2
3.下列语句中,正确的是( )
A.长度相等的两条弧是等弧 B.相等的圆周角所对的弧相等
C.相等的弧所对的圆心角相等 D.平分弦的直径垂直于弦
4.如图,已知⊙O的弦AB、DC的延长线相交于点E,∠AOD=128°,∠E=40°,则∠BDC的度数是( )
A.16° B.20° C.24° D.32°
5.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,若∠C=124°,则∠B的度数为( )
A.56° B.68° C.72° D.78°
6.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=30°,半径为2,则弦CD的长为( )
A.2 B.﹣1 C. D.4
7.如图,在以AB为直径的⊙O中,点C为圆上的一点,=3,弦CD⊥AB于点E,弦AF交CE于点H,交BC于点G.若点H是AG的中点,则∠CBF的度数为( )
A.18° B.21° C.22.5° D.30°
8.如图,在Rt△ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且=,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
A.92° B.108° C.112° D.124°
9.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
10.如图,将⊙O上的沿弦BC翻折交半径OA于点D,再将沿BD翻折交BC于点E,连接DE.若AD=2OD,则的值为( )
A. B. C. D.
11.如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为( )
A.(0,5) B.(0,5) C.(0,) D.(0,)
12.在半径为3cm的⊙O中,若弦AB=3cm,则弦AB所对的圆周角的度数为( )
A.30° B.45° C.30°或150° D.45°或135°
二.填空题
13.如图,AB为⊙O的直径,点C、D在⊙O上,若∠CBA=70°,则∠D的度数是 .
14.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= .
15.如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长相交于点F.若∠A=50°,∠E=45°,则∠DCB= ,∠F= .
16.如图,直线l与⊙O相交于点B、D,点A、C是直线l两侧的圆弧上的动点,若⊙O的半径为1,∠A=30°,那么四边形ABCD的面积的最大值是 .
17.如图,在平面直角坐标系中,⊙M经过原点,且与x轴交于点A(﹣4,0),与y轴交于点B(0,2),点C在第二象限⊙M上,且∠AOC=60°,则OC= .
18.如图,四边形ABCD内接于⊙O,AB=AD,其外角∠EAD的平分线交CD的延长线于点F,CD=10,AF=5,则DF的长为 .
三.解答题
19.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC= °;∠DAC= °
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
20.如图,AB是⊙O的直径,C、D为⊙O上的点,且AD平分∠CAB,作DE⊥AB于点E.
(1)求证:AC∥OD;
(2)若OE=4,求AC的长.
21.如图,以P(0,3)为圆心,6为半径的⊙P交x轴于点A、B,交y轴于点C、D,连接BP并延长交⊙P于点E,连接DE交x轴于点F.
(1)求∠CDE的度数;
(2)求△BEF的面积.
22.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,连接MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
24.如图1,在Rt△ABC中,∠B=90°,∠C=40°,以AB为直径画⊙O交AC于点D,E是线段AB上的动点,延长DE交⊙O于F点,连接AF.
(1)如图1,求∠F的度数;
(2)如图2,当AE=AD时,求∠DFO的度数.
25.如图,∠BAO=90°,AB=8,动点P在射线AO上,以PA为半径的半圆P交射线AO于另一点C,CD∥BP交半圆P于另一点D,BE∥AO交射线PD于点E,EF⊥AO于点F,连接BD,设AP=m.
(1)求证:∠BDP=90°.
(2)若m=4,求BE的长.
(3)在点P的整个运动过程中,当AF=3CF时,求出所有符合条件的m的值.
参考答案
一.选择题
1.解:∵∠C=40°,
∴∠AOB=80°,
∵OA=OB,
∴∠OAB=∠OBA=50°.
故选:B.
2.解:∵圆的内接四边形对角互补,
∴∠A+∠C=∠B+∠D=180°,
∴∠A:∠B:∠C:∠D的可能的值是4:3:1:2.
故选:C.
3.解:A、长度相等的两条弧不一定为等弧,所以A选项错误;
B、在同圆或等圆中,相等的圆周角所对的弧相等,所以B选项错误;
C、相等的弧所对的圆心角相等,所以C选项正确;
D、平分弦(非直径)的直径垂直于弦,所以D选项错误.
故选:C.
4.解:∵∠ABD是所对的圆周角,
∴∠ABD=∠AOD=×128°=64°,
∵∠ABD是△BDE的外角,
∴∠BDC=∠ABD﹣∠E=64°﹣40°=24°,
故选:C.
5.解:∵∠C=124°,
∴∠A=180°﹣124°=56°,
∴∠BOD=2∠A=112°,
∵OD∥BC,
∴∠CDO=180°﹣124°=56°,
∴∠B=360°﹣124°﹣56°﹣112°=68°.
故选:B.
6.解:∵∠BOC=2∠A,∠A=30°,
∴∠BOC=60°,
∵AB是⊙O的直径,AB⊥CD,
∴CE=DE=CD,∠OCE=30°,
∵半径OC=2,
∴OE=OC=1,
∴CE===,
∴CD=2CE=2.
故选:C.
7.解:∵AB是直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∵=3,
∴∠CAB=3∠ABC,
∴∠ABC=22.5°,∠CAB=67.5°,
∵CD⊥AB,
∴∠ACE=22.5°,
∵点H是AG的中点,∠ACB=90°,
∴AH=CH=HG,
∴∠CAH=∠ACE=22.5°,
∵∠CAF=∠CBF,
∴∠CBF=22.5°,
故选:C.
8.解:解法一、连接OD,
∵=,
∴∠DOC=∠EOC,
∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∴∠DOC=2∠B=72°,
∴∠EOC=∠DOC=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
解法二、∵∠ACB=90°,∠A=54°,
∴∠B=90°﹣∠A=36°,
∵=,
∴∠COE=2∠B=72°,
∵OE⊥EF,
∴∠OEF=90°,
∵∠ACB=90°,
∴∠BCF=90°,
∴∠F=360°﹣∠OEF﹣∠BCF﹣∠EOC=360°﹣90°﹣90°﹣72°=108°;
故选:B.
9.解:连接PA,PB,PC,过P作PD⊥AB于D,PE⊥OC于E,
∵∠ACB=60°,
∴∠APB=120°,
∵PA=PB,
∴∠PAB=∠PBA=30°,
∵A(﹣5,0),B(1,0),
∴AB=6,
∴AD=BD=3,
∴PD=,PA=PB=PC=2,
∵PD⊥AB,PE⊥OC,∠AOC=90°,
∴四边形PEOD是矩形,
∴OE=PD=,PE=OD=2,
∴CE===2,
∴OC=CE+OE=2+,
∴点C的纵坐标为2+,
故选:B.
10.解:如图,连接AC,CD,OC,过点C作CH⊥AB于H.设OA=3a,则AB=6a.
∵在同圆或等圆中,∠ABC所对的弧有,,,
∴AC=CD=DE,
∵CH⊥AD,
∴AH=DH,
∵AD=2OD,
∴AH=DH=OD=a,
在Rt△OCH中,CH===a,
在Rt△ACH中,AC===a,
∴===,
故选:D.
11.解:连接CA,OA,
∵∠OBC=30°,
∴∠CAO=60°,
又∵CA=AO,
∴△CAO是等边三角形,
∴CO=AO=5,
∴点C的坐标为:(0,5).
故选:A.
12.解:如图所示,
连接OA,OB,
则OA=OB=3cm,
∵AB=3cm,
∴OA2+OB2=AB2,
∴∠AOB=90°,
∴劣弧AB的度数是90°,优弧AB的度数是360°﹣90°=270°,
∴弦AB对的圆周角的度数是45°或135°,
故选:D.
二.填空题
13.解:∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CBA=70°,
∴∠A=20°,
∴∠D=∠A=20°.
故答案为20°.
14.解:连接OD,
∵AD∥OC,
∴∠DAB=∠BOC=50°,
∵OA=OD
∴∠AOD=180°﹣2∠DAB=80°,
∴∠ACD=∠AOD=40°
故答案为40°
15.解:∵四边形ABCD内接于⊙O,
∴∠A+∠DCB=180°,
∵∠A=50°,
∴∠DCB=180°﹣50°=130°,
∵∠CBF是△ABE的外角,∠A=50°,∠E=45°,
∴∠CBF=∠A+∠E=95°,
∴∠F=∠DCB﹣∠CBF=35°,
故答案为:130°;35°.
16.解:当A点和C点到BD的距离最大时,四边形ABCD的面积最大,此时A点和C点为BD所对弧的中点,
∴AC为⊙O的直径,如图,
∴AC⊥BD,
∵∠BAC=30°,
∴∠BOC=30°,
在Rt△OBH中,BH=OB=,
∴S△ABC= BH AC=×2×=,
∴四边形ABCD的面积=2×=1,
∴四边形ABCD的面积的最大值为1.
故答案为1.
17.解:连接AC,CM,AB,过点C作CH⊥OA于H,设OC=a.
∵∠AOB=90°,
∴AB是直径,
∵A(﹣4,0),B(0,2),
∴AB===2,
∵∠AMC=2∠AOC=120°,
∴AC=AM=,
在Rt△COH中,OH=a,CH=OH=a,
∴AH=4﹣a,
在Rt△ACH中,AC2=AH2+CH2,
∴15=(4﹣a)2+(a)2,
∴a=2+或2﹣(因为OC>OB,所以2﹣舍弃),
∴OC=2+.
故答案为:2+.
18.解:连接AC,
∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
又∠BAD+∠EAD=180°,
∴∠EAD=∠BCD,
∵AB=AD,
∴=,
∴∠ACB=∠ACD=BCD,
∵AF平分∠EAD,
∴∠FAD=∠EAD,
∴∠FCA=∠FAD,
又∠AFC=∠DFA,
∴DF=5﹣5,
故答案为:5﹣5.
三.解答题
19.(1)解:∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=70°,
∴∠ADC=180°﹣∠ABC=180°﹣70°=110°;
∵AC⊥BD,
∴∠CBD=90°﹣∠ACB=20°,
∴∠DAC=∠DBC=20°;
故答案为:110,20;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=∠CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
∴,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
20.(1)证明:∵AD平分∠CAB,
∴∠OAC=2∠OAD.
∵∠BOD=2∠BAD,
∴∠BOD=∠OAC,
∴AC∥OD.
(2)解:作OF⊥AC于点F,如图所示:
则AF=AC,
∵AC∥OD,
∴∠DOE=∠OAF.
在△DOE和△OAF中,,
∴△DOE≌△OAF(AAS),
∴OE=AF=AC,
∴AC=2OE=8.
21.解:(1)∵P(0,3),
∴OP=3,
∵⊙P的半径是6,
∴PB=6,
∴OP=PB,
∵x轴⊥y轴,
∴∠POB=90°,
∴∠PBO=30°,
∴∠BPO=90°﹣30°=60°,
∵PE=PD,∠E+∠CDE=∠BPO,
∴∠CDE=∠E=60°=30°;
(2)连接PF,
∵∠PBO=∠E=30°,
∴BF=EF,
∵PE=PB=6,
∴PF⊥BE,
即∠EPF=90°,
∴EF=2PF,
由勾股定理得:PE2+PF2=EF2,
即62+PF2=(2PF)2,
解得:PF=2,
EF=BF=4,
∴△BEF的面积是==12.
22.(1)证明:连接AE,如图,
∵AC为⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
而AB=AC,
∴BE=CE;
(2)连接DE,如图,
∵BE=CE=3,
∴BC=6,
∵∠BED=∠BAC,
而∠DBE=∠CBA,
∴BA=9,
∴AC=BA=9.
23.解:(1)设⊙O的半径长为r,
则OD=r,OE=r﹣8,
∵AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,
∴DE=12,
∴OD2=OE2+DE2,
即r2=(r﹣8)2+122,
解得,r=13,
即⊙O的半径是13;
(2)连接BC,
∵∠DMB=∠D,∠DMB=∠DCB,
∴∠D=∠DCB,
∵AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,
∴CE=DE=12,∠CEB=∠DEO,
∴△CEB≌△DEO(ASA),
∴OE=BE=0.5OB,
设⊙O的半径长为r,
则r2=122+(0.5r)2,
解得,r=或r=﹣8(舍去),
∴OE=4.
24.解:(1)如图1,连接OD,
在Rt△ABC中,∠B=90°,∠C=40°,
∴∠BAC=50°,
∵OA=OD,
∴∠ODA=∠OAD=50°,
∴∠AOD=180°﹣50°﹣50°=80°,
∴∠F=∠AOD=40°;
(2)如图2,连接OD,
在Rt△ABC中,∠B=90°,∠C=40°,
∴∠BAC=50°,
∵OA=OD,
∴∠ODA=∠OAD=50°,
∵AE=AD,
∴∠ADE=∠AED=(180°﹣50°)=65°,
∴∠ODF=∠ADE﹣∠ODA=65°﹣50°=15°,
∵OF=OD,
∴∠DFO=∠FDO=15°.
25.解:(1)如图1,∵PA=PC=PD,
∴∠PDC=∠PCD,
∵CD∥BP,
∴∠BPA=∠PCD、∠BPD=∠PDC,
∴∠BPA=∠BPD,
∵BP=BP,
∴△BAP≌△BDP(SAS),
∴∠BDP=∠BAP=90°.
(2)∵∠BAO=90°,BE∥AO,
∴∠ABE=∠BAO=90°,
∵EF⊥AO,
∴∠EFA=90°,
∴四边形ABEF是矩形,
设BE=AF=x,则PF=x﹣4,
∵∠BDP=90°,
∴∠BDE=90°=∠PFE,
∵BE∥AO,
∴∠BED=∠EPF,
∵△BAP≌△BDP,
∴BD=BA=EF=8,
∴△BDE≌△EFP,
∴PE=BE=x,
在Rt△PFE中,PF2+FE2=PE2,即(x﹣4)2+82=x2,
解得:x=10,
∴BE的长为10.
(3)如图1,当点C在AF的左侧时,
∵AF=3CF,则AC=2CF,
∴CF=AP=PC=m,
∴PF=2m,PE=BE=AF=3m,
在Rt△PEF中,由PF2+EF2=PE2可得(2m)2+82=(3m)2,
解得:m=(负值舍去);
如图2,当点C在AF的右侧时,
∵AF=3CF,
∴AC=4CF,
∴CF=AP=PC=m,
∴PF=m﹣m=m,PE=BE=AF=m+m=m,
在Rt△PEF中,由PF2+EF2=PE2可得(m)2+82=(m)2,
解得:m=4(负值舍去);
综上,m的值为或4.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
