2022-2023学年人教版八年级数学上册 12.2三角形全等的判定 自主达标测评 (含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 12.2三角形全等的判定 自主达标测评 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 256.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 18:34:07 | ||
图片预览


文档简介
2022-2023学年人教版八年级数学上册《12.2三角形全等的判定》自主达标测评(附答案)
一.选择题(共10小题,满分40分)
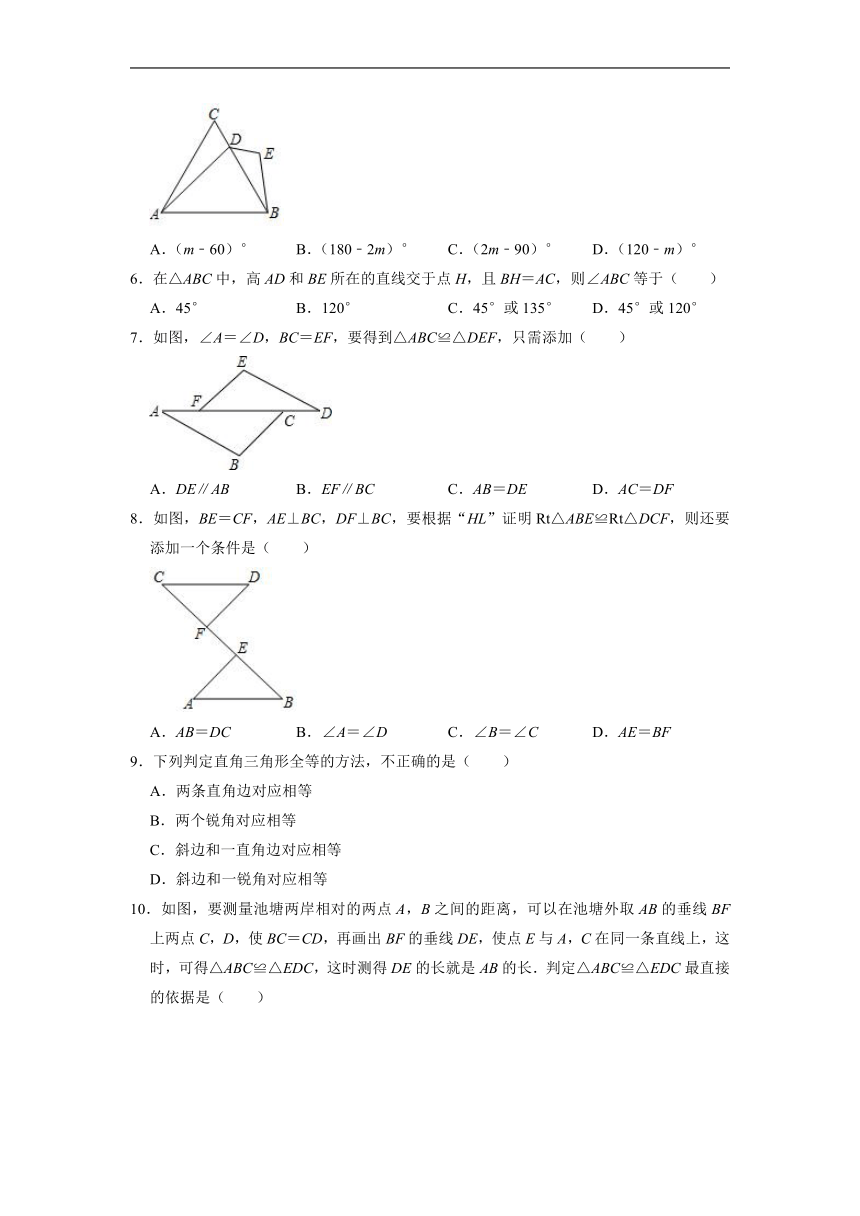
1.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28 B.29 C.30 D.31
2.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45° B.30° C.22.5° D.15°
3.下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
4.如图,等腰直角△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,NE.下列结论:①AE=AF;②AM⊥EF;③△AEF是等边三角形;④DF=DN,⑤AD∥NE.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
5.如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A.(m﹣60)° B.(180﹣2m)° C.(2m﹣90)° D.(120﹣m)°
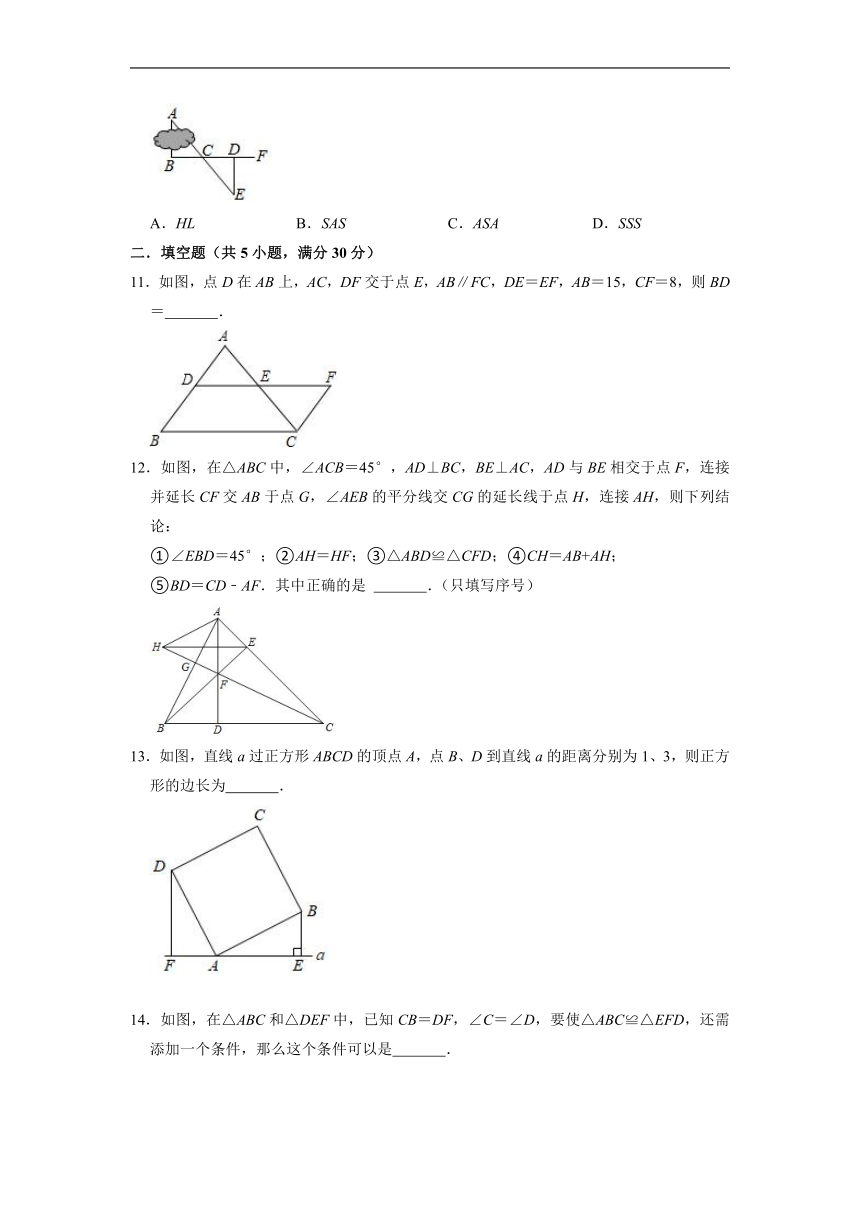
6.在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A.45° B.120° C.45°或135° D.45°或120°
7.如图,∠A=∠D,BC=EF,要得到△ABC≌△DEF,只需添加( )
A.DE∥AB B.EF∥BC C.AB=DE D.AC=DF
8.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=BF
9.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.斜边和一直角边对应相等
D.斜边和一锐角对应相等
10.如图,要测量池塘两岸相对的两点A,B之间的距离,可以在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使点E与A,C在同一条直线上,这时,可得△ABC≌△EDC,这时测得DE的长就是AB的长.判定△ABC≌△EDC最直接的依据是( )
A.HL B.SAS C.ASA D.SSS
二.填空题(共5小题,满分30分)
11.如图,点D在AB上,AC,DF交于点E,AB∥FC,DE=EF,AB=15,CF=8,则BD= .
12.如图,在△ABC中,∠ACB=45°,AD⊥BC,BE⊥AC,AD与BE相交于点F,连接并延长CF交AB于点G,∠AEB的平分线交CG的延长线于点H,连接AH,则下列结论:
①∠EBD=45°;②AH=HF;③△ABD≌△CFD;④CH=AB+AH;
⑤BD=CD﹣AF.其中正确的是 .(只填写序号)
13.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为1、3,则正方形的边长为 .
14.如图,在△ABC和△DEF中,已知CB=DF,∠C=∠D,要使△ABC≌△EFD,还需添加一个条件,那么这个条件可以是 .
15.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是 (填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.
三.解答题(共5小题,满分50分)
16.如图,已知AB=AC,BD=CE,请说明△ABE≌△ACD.
17.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
18.如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
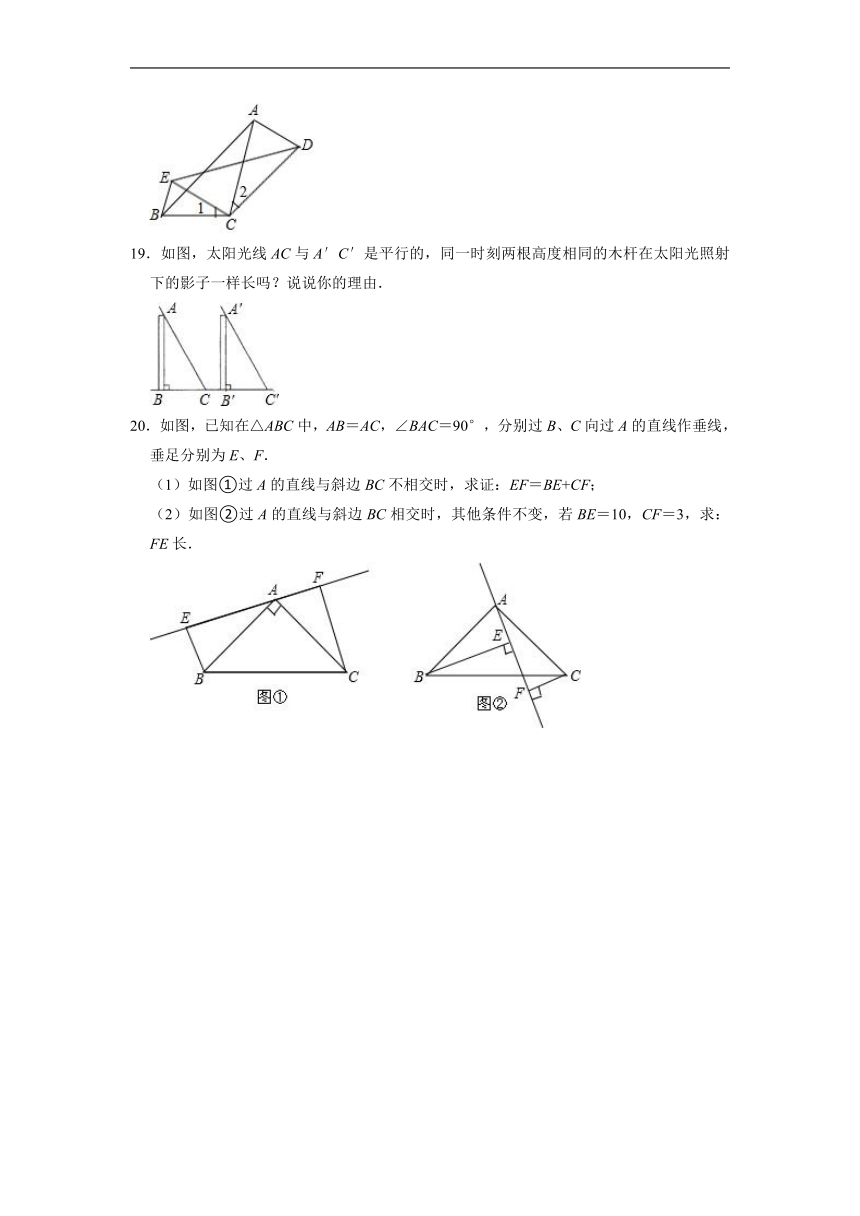
19.如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.
20.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长.
参考答案
一.选择题(共10小题,满分40分)
1.解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
2.解:
连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
3.解:①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.可以用“倍长中线法”,用SAS定理,判断两个三角形全等;
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选:A.
4.解:∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°
∴∠AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,故①正确;③错误,
∵M为EF的中点,
∴AM⊥EF,故②正确;
∵AM⊥EF,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,故④正确;
∵∠BAM=∠BNM=67.5°,
∴BA=BN,
∵∠EBA=∠EBN,BE=BE,
∴△EBA≌△EBN(SAS),
∴∠BNE=∠BAE=90°,
∴∠ENC=∠ADC=90°,
∴AD∥EN.故⑤正确,
故选:D.
5.解:如图,连接AE.
∵△ABC是等边三角形,
∴∠C=∠ABC=60°,
∵∠ADB=m°,∠BDE=(180﹣2m)°,
∴∠ADC=180°﹣m°,∠ADE=180°﹣m°,
∴∠ADC=∠ADE,
∵AD=AD,DC=DE,
∴△ADC≌△ADE(SAS),
∴∠C=∠AED=60°,∠DAC=∠DAE,
∴∠DEA=∠DBA,
∴∠BDE=∠BAE=180°﹣2m,
∵AE=AC=AB,
∴∠ABE=∠AEB=(180°﹣180°+2m)=m,
∴∠DBE=∠ABE﹣∠ABC=(m﹣60)°,
故选:A.
6.解:分为三种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中
,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°﹣45°=135°;
③如图3中,
∵高AD和BE所在的直线交于点H,
∴∠HDB=∠ADC=∠HEA=90°,
∴∠H+∠DAC=90°,∠H+∠HBD=90°,
∴∠DAC=∠HBD,
在△DAC和△DBH中,
,
∴△DAC≌△DBH(AAS),
∴AD=BD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
故选:C.
7.解:A.∵DE∥AB,
∴∠A=∠D,
由∠A=∠D,BC=EF不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
B.∵EF∥BC,
∴∠EFC=∠BCA,
∠A=∠D,∠EFC=∠BCA,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项符合题意;
C.BC=EF,AB=DE,∠A=∠D,不符合全等三角形的判定定理,能推出△ABC≌△DEF,故本选项不符合题意;
D.AC=DF,BC=EF,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△CDE,故本选项不符合题意;
故选:B.
8.解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故选:A.
9.解:A、根据SAS可以判定三角形全等,本选项不符合题意.
B、AA不能判定三角形全等,本选项符合题意.
C、根据HL可以判定三角形全等,本选项不符合题意.
D、根据AAS可以判定三角形全等,本选项不符合题意.
故选:B.
10.解:因为证明在△ABC≌△EDC用到的条件是:BC=CD,∠ABC=∠EDC=90°,∠ACB=∠ECD(对顶角相等),
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:C.
二.填空题(共5小题,满分30分)
11.解:∵AB∥FC,
∴∠ADE=∠F
又∵DE=EF,∠AED=∠CEF,
∴△ADE≌△CFE,
∴AD=CF,
∵AB=15,CF=8,
∴BD=AB﹣AD=15﹣8=7.
故答案是:7.
12.解:①∵∠ACB=45°,BE⊥AC,
∴∠BEA=∠BEC=90°,
∴∠EBD=45°,故①正确;
②∵EH是∠AEB的角平分线,
∴∠HEB=∠AEB=45°,
∴∠HEB=∠EBC=45°,
∴EH∥BC,
∵AD⊥BC,
∴AD⊥EH,
∴∠AFE=∠EAF=45°,
∴AE=EF,
∴EH是AF的垂直平分线,
∴AH=HF;故②正确;
③∵∠BDF=90°,∠FBD=45°,
∴∠DFB=45°,
∴DB=DF,
∵∠ACB=45°,AD⊥BC,
∴∠DAC=45°,
∴AD=CD,
在△ABD与△CFD中,
,
∴△ABD≌△CFD(SAS),故③正确;
④∵△ABD≌△CFD,
∴AB=CF,
∴CH=CF+FH=AB+AH;故④正确;
⑤∵DF=AD﹣AF,
∴BD=CD﹣AF.故⑤正确.
综上所述①②③④⑤正确.
故答案为:①②③④⑤.
13.解:在正方形ABCD中,AD=AB,
∵DF⊥AF,BE⊥AE,
∴∠AFD=∠AEB=90°,∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在Rt△AFD和Rt△BEA中,
,
∴Rt△AFD≌Rt△BEA(AAS),
∴DF=AE=3,AF=BE=1,
AB=.
故答案为:.
14.解:要使△ABC≌△EFD,已知CB=DF,∠C=∠D,
则可以添加AC=ED,运用SAS来判定其全等;
也可添加一组角∠A=∠FED或∠ABC=∠F运用AAS来判定其全等.
故答案为:AC=ED或∠A=∠FED或∠ABC=∠F.
15.解:∵AB=AC,
∴∠EBC=∠DCB,
又∵BD平分∠ABC,∠CE平分∠ACB,
∴∠DBC=∠ECB,
∵∠BEC=180°﹣∠EBC﹣∠ECB,∠CDB=180°﹣∠DCB﹣∠DBC,
∴∠BEC=∠CDB.
在△EBC和△DCB中,,
∴△EBC≌△DCB(AAS).
即①成立;
在△BAD和△BCD中,仅有,
不满足全等的条件,
即②不一定成立;
∵△EBC≌△DCB,
∴BD=CE.
在△BDA和△CEA中,,
∴△BDA≌△CEA(SAS).
即③成立;
∵△BDA≌△CEA,
∴AD=AE,
∵AB=AC,
∴BE=CD.
在△BOE和△COD中,,
∴△BOE≌△COD(AAS).
即④成立;
在△ACE和△BCE中,仅有,
不满足全等的条件,
即⑤不一定成立.
综上可知:一定成立的有①③④.
故答案为:①③④.
三.解答题(共5小题,满分50分)
16.解:∵AB=AC,BD=CE,
∴AD=AE.
又∵∠A=∠A,
∴△ABE≌△ACD(SAS).
17.解:∵MS⊥PS,MN⊥SN,PQ⊥SN,
∴∠M+∠MSN=∠MSN+∠PSQ,
∴∠M=∠PSQ;
在△MNS与△SQP中,
,
∴△MNS≌△SQP(AAS).
18.证明:∵∠1=∠2,
∴∠1+ECA=∠2+∠ACE,
即∠ACB=∠DCE,
在△ABC和△DEC中,
∵
∴△ABC≌△DEC(SAS).
∴DE=AB.
19.解:影子一样长.
证明:
∵AB⊥BC,A′B′⊥B′C′
∴∠ABC=∠A′B′C′=90°
∵AC∥A′C′
∴∠ACB=∠A′C′B′
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(AAS)
∴BC=B′C′
即影子一样长.
20.(1)证明:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠EBA+∠EAB=90°,
∴∠CAF=∠EBA,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC(AAS).
∴EA=FC,BE=AF.
∴EF=EB+CF.
(2)解:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠ABE+∠EAB=90°,
∴∠CAF=∠ABE,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC(AAS).
∴EA=FC=3,BE=AF=10.
∴EF=AF﹣CF=10﹣3=7.
一.选择题(共10小题,满分40分)
1.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28 B.29 C.30 D.31
2.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45° B.30° C.22.5° D.15°
3.下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A.①② B.②③ C.①③ D.①②③
4.如图,等腰直角△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,NE.下列结论:①AE=AF;②AM⊥EF;③△AEF是等边三角形;④DF=DN,⑤AD∥NE.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
5.如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A.(m﹣60)° B.(180﹣2m)° C.(2m﹣90)° D.(120﹣m)°
6.在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A.45° B.120° C.45°或135° D.45°或120°
7.如图,∠A=∠D,BC=EF,要得到△ABC≌△DEF,只需添加( )
A.DE∥AB B.EF∥BC C.AB=DE D.AC=DF
8.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还要添加一个条件是( )
A.AB=DC B.∠A=∠D C.∠B=∠C D.AE=BF
9.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.两个锐角对应相等
C.斜边和一直角边对应相等
D.斜边和一锐角对应相等
10.如图,要测量池塘两岸相对的两点A,B之间的距离,可以在池塘外取AB的垂线BF上两点C,D,使BC=CD,再画出BF的垂线DE,使点E与A,C在同一条直线上,这时,可得△ABC≌△EDC,这时测得DE的长就是AB的长.判定△ABC≌△EDC最直接的依据是( )
A.HL B.SAS C.ASA D.SSS
二.填空题(共5小题,满分30分)
11.如图,点D在AB上,AC,DF交于点E,AB∥FC,DE=EF,AB=15,CF=8,则BD= .
12.如图,在△ABC中,∠ACB=45°,AD⊥BC,BE⊥AC,AD与BE相交于点F,连接并延长CF交AB于点G,∠AEB的平分线交CG的延长线于点H,连接AH,则下列结论:
①∠EBD=45°;②AH=HF;③△ABD≌△CFD;④CH=AB+AH;
⑤BD=CD﹣AF.其中正确的是 .(只填写序号)
13.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为1、3,则正方形的边长为 .
14.如图,在△ABC和△DEF中,已知CB=DF,∠C=∠D,要使△ABC≌△EFD,还需添加一个条件,那么这个条件可以是 .
15.如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是 (填代号).
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.
三.解答题(共5小题,满分50分)
16.如图,已知AB=AC,BD=CE,请说明△ABE≌△ACD.
17.已知:如图,MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N、Q,且MS=PS.求证:△MNS≌△SQP.
18.如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
19.如图,太阳光线AC与A′C′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.
20.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.
(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;
(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE长.
参考答案
一.选择题(共10小题,满分40分)
1.解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
2.解:
连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
3.解:①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.可以用“倍长中线法”,用SAS定理,判断两个三角形全等;
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选:A.
4.解:∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°
∴∠AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,故①正确;③错误,
∵M为EF的中点,
∴AM⊥EF,故②正确;
∵AM⊥EF,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,故④正确;
∵∠BAM=∠BNM=67.5°,
∴BA=BN,
∵∠EBA=∠EBN,BE=BE,
∴△EBA≌△EBN(SAS),
∴∠BNE=∠BAE=90°,
∴∠ENC=∠ADC=90°,
∴AD∥EN.故⑤正确,
故选:D.
5.解:如图,连接AE.
∵△ABC是等边三角形,
∴∠C=∠ABC=60°,
∵∠ADB=m°,∠BDE=(180﹣2m)°,
∴∠ADC=180°﹣m°,∠ADE=180°﹣m°,
∴∠ADC=∠ADE,
∵AD=AD,DC=DE,
∴△ADC≌△ADE(SAS),
∴∠C=∠AED=60°,∠DAC=∠DAE,
∴∠DEA=∠DBA,
∴∠BDE=∠BAE=180°﹣2m,
∵AE=AC=AB,
∴∠ABE=∠AEB=(180°﹣180°+2m)=m,
∴∠DBE=∠ABE﹣∠ABC=(m﹣60)°,
故选:A.
6.解:分为三种情况:
①如图1,
∵AD、BE是△ABC的高,
∴∠ADC=∠BDH=90°,∠BEC=90°,
∴∠C+∠CAD=90°,∠C+∠HBD=90°,
∴∠CAD=∠HBD,
在△HBD和△CAD中
,
∴△HBD≌△CAD(AAS),
∴BD=AD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
②如图2,
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠HDB=∠AEH=90°,
∴∠H+∠HAE=∠C+∠HAE=90°,
∴∠H=∠C,
∵在△HBD和△CAD中,
,
∴△HBD≌△CAD(AAS),
∴AD=BD,
∴∠DAB=∠DBA,
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°﹣45°=135°;
③如图3中,
∵高AD和BE所在的直线交于点H,
∴∠HDB=∠ADC=∠HEA=90°,
∴∠H+∠DAC=90°,∠H+∠HBD=90°,
∴∠DAC=∠HBD,
在△DAC和△DBH中,
,
∴△DAC≌△DBH(AAS),
∴AD=BD,
∵∠ADB=90°,
∴∠ABC=∠BAD=45°,
故选:C.
7.解:A.∵DE∥AB,
∴∠A=∠D,
由∠A=∠D,BC=EF不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项不符合题意;
B.∵EF∥BC,
∴∠EFC=∠BCA,
∠A=∠D,∠EFC=∠BCA,BC=EF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项符合题意;
C.BC=EF,AB=DE,∠A=∠D,不符合全等三角形的判定定理,能推出△ABC≌△DEF,故本选项不符合题意;
D.AC=DF,BC=EF,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△CDE,故本选项不符合题意;
故选:B.
8.解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故选:A.
9.解:A、根据SAS可以判定三角形全等,本选项不符合题意.
B、AA不能判定三角形全等,本选项符合题意.
C、根据HL可以判定三角形全等,本选项不符合题意.
D、根据AAS可以判定三角形全等,本选项不符合题意.
故选:B.
10.解:因为证明在△ABC≌△EDC用到的条件是:BC=CD,∠ABC=∠EDC=90°,∠ACB=∠ECD(对顶角相等),
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:C.
二.填空题(共5小题,满分30分)
11.解:∵AB∥FC,
∴∠ADE=∠F
又∵DE=EF,∠AED=∠CEF,
∴△ADE≌△CFE,
∴AD=CF,
∵AB=15,CF=8,
∴BD=AB﹣AD=15﹣8=7.
故答案是:7.
12.解:①∵∠ACB=45°,BE⊥AC,
∴∠BEA=∠BEC=90°,
∴∠EBD=45°,故①正确;
②∵EH是∠AEB的角平分线,
∴∠HEB=∠AEB=45°,
∴∠HEB=∠EBC=45°,
∴EH∥BC,
∵AD⊥BC,
∴AD⊥EH,
∴∠AFE=∠EAF=45°,
∴AE=EF,
∴EH是AF的垂直平分线,
∴AH=HF;故②正确;
③∵∠BDF=90°,∠FBD=45°,
∴∠DFB=45°,
∴DB=DF,
∵∠ACB=45°,AD⊥BC,
∴∠DAC=45°,
∴AD=CD,
在△ABD与△CFD中,
,
∴△ABD≌△CFD(SAS),故③正确;
④∵△ABD≌△CFD,
∴AB=CF,
∴CH=CF+FH=AB+AH;故④正确;
⑤∵DF=AD﹣AF,
∴BD=CD﹣AF.故⑤正确.
综上所述①②③④⑤正确.
故答案为:①②③④⑤.
13.解:在正方形ABCD中,AD=AB,
∵DF⊥AF,BE⊥AE,
∴∠AFD=∠AEB=90°,∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在Rt△AFD和Rt△BEA中,
,
∴Rt△AFD≌Rt△BEA(AAS),
∴DF=AE=3,AF=BE=1,
AB=.
故答案为:.
14.解:要使△ABC≌△EFD,已知CB=DF,∠C=∠D,
则可以添加AC=ED,运用SAS来判定其全等;
也可添加一组角∠A=∠FED或∠ABC=∠F运用AAS来判定其全等.
故答案为:AC=ED或∠A=∠FED或∠ABC=∠F.
15.解:∵AB=AC,
∴∠EBC=∠DCB,
又∵BD平分∠ABC,∠CE平分∠ACB,
∴∠DBC=∠ECB,
∵∠BEC=180°﹣∠EBC﹣∠ECB,∠CDB=180°﹣∠DCB﹣∠DBC,
∴∠BEC=∠CDB.
在△EBC和△DCB中,,
∴△EBC≌△DCB(AAS).
即①成立;
在△BAD和△BCD中,仅有,
不满足全等的条件,
即②不一定成立;
∵△EBC≌△DCB,
∴BD=CE.
在△BDA和△CEA中,,
∴△BDA≌△CEA(SAS).
即③成立;
∵△BDA≌△CEA,
∴AD=AE,
∵AB=AC,
∴BE=CD.
在△BOE和△COD中,,
∴△BOE≌△COD(AAS).
即④成立;
在△ACE和△BCE中,仅有,
不满足全等的条件,
即⑤不一定成立.
综上可知:一定成立的有①③④.
故答案为:①③④.
三.解答题(共5小题,满分50分)
16.解:∵AB=AC,BD=CE,
∴AD=AE.
又∵∠A=∠A,
∴△ABE≌△ACD(SAS).
17.解:∵MS⊥PS,MN⊥SN,PQ⊥SN,
∴∠M+∠MSN=∠MSN+∠PSQ,
∴∠M=∠PSQ;
在△MNS与△SQP中,
,
∴△MNS≌△SQP(AAS).
18.证明:∵∠1=∠2,
∴∠1+ECA=∠2+∠ACE,
即∠ACB=∠DCE,
在△ABC和△DEC中,
∵
∴△ABC≌△DEC(SAS).
∴DE=AB.
19.解:影子一样长.
证明:
∵AB⊥BC,A′B′⊥B′C′
∴∠ABC=∠A′B′C′=90°
∵AC∥A′C′
∴∠ACB=∠A′C′B′
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(AAS)
∴BC=B′C′
即影子一样长.
20.(1)证明:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠EBA+∠EAB=90°,
∴∠CAF=∠EBA,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC(AAS).
∴EA=FC,BE=AF.
∴EF=EB+CF.
(2)解:∵BE⊥EA,CF⊥AF,
∴∠BAC=∠BEA=∠CFE=90°,
∴∠EAB+∠CAF=90°,∠ABE+∠EAB=90°,
∴∠CAF=∠ABE,
在△ABE和△AFC中,
∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,
∴△BEA≌△AFC(AAS).
∴EA=FC=3,BE=AF=10.
∴EF=AF﹣CF=10﹣3=7.
