2022-2023学年人教版八年级数学上册12.2三角形全等的判定 同步达标测试题(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2三角形全等的判定 同步达标测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 166.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览



文档简介
2022-2023学年人教版八年级数学上册《12.2三角形全等的判定》同步达标测试题(附答案)
一.选择题(共8小题,满分40分)
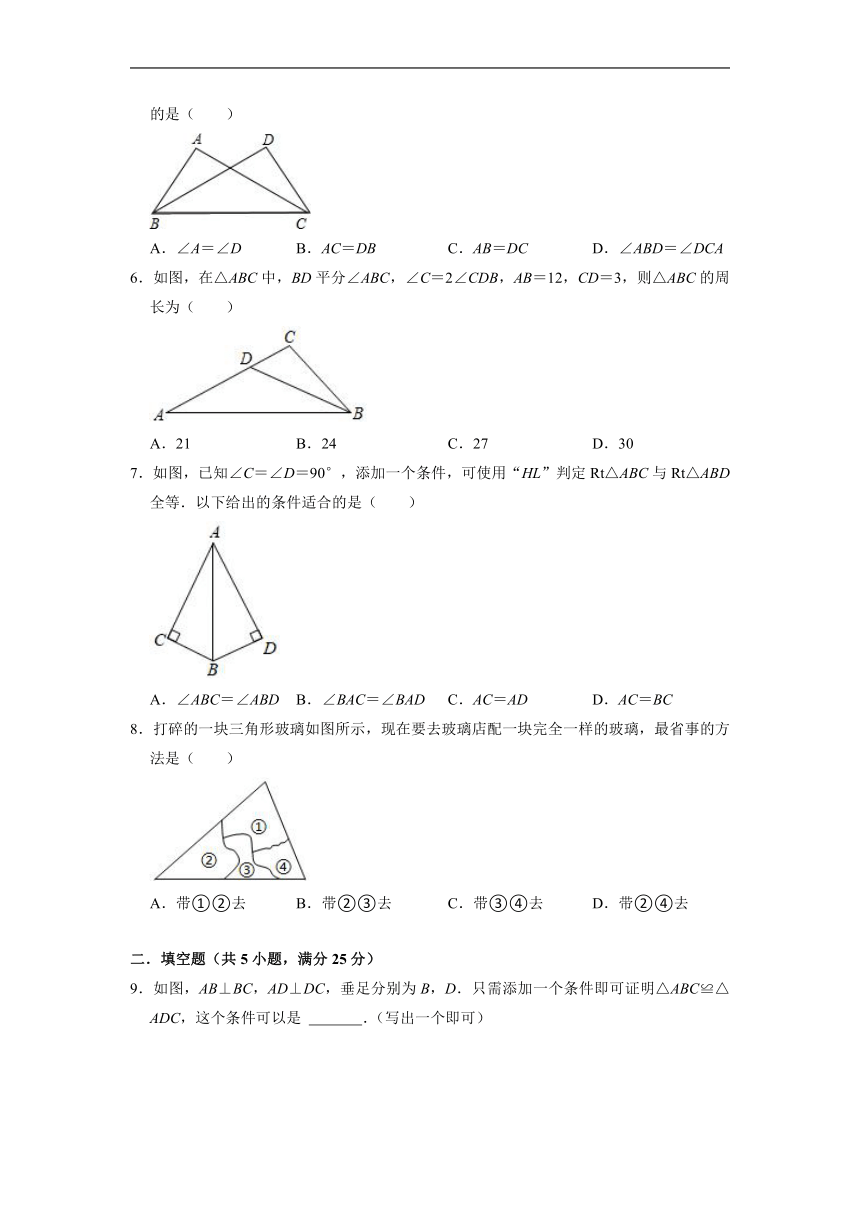
1.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠FAC=40°,则∠BFE=( )
A.35° B.40° C.45° D.50°
2.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS B.SAS C.ASA D.SSS
3.如图,在△ABC和△DEF中,点B、F、C、D在同条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E B.AC=DF C.∠ACD=∠BFE D.BC=EF
4.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
5.如图,点A、D在线段BC的同侧,连接AB、AC、DB、DC,已知∠ABC=∠DCB,老师要求同学们补充一个条件使△ABC≌△DCB.以下是四个同学补充的条件,其中错误的是( )
A.∠A=∠D B.AC=DB C.AB=DC D.∠ABD=∠DCA
6.如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为( )
A.21 B.24 C.27 D.30
7.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.∠ABC=∠ABD B.∠BAC=∠BAD C.AC=AD D.AC=BC
8.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①②去 B.带②③去 C.带③④去 D.带②④去
二.填空题(共5小题,满分25分)
9.如图,AB⊥BC,AD⊥DC,垂足分别为B,D.只需添加一个条件即可证明△ABC≌△ADC,这个条件可以是 .(写出一个即可)
已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
11.如图,C是线段AB上的一点,△ACD和△BCE都是等边三角形,AE交CD于M,BD交CE于N,交AE于O,则①DB=AE;②∠AMC=∠DNC;③∠AOB=60°;④DN=AM;⑤△CMN是等边三角形.其中,正确的有 .
12.如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= .
13.如图,AB与CD相交于点O,OC=OD.若要得到△AOC≌△BOD,则应添加的条件是 .(写出一种情况即可)
三.解答题(共7小题,满分55分)
14.如图,已知BD平分∠ABC,∠A=∠C.
求证:△ABD≌△CBD.
15.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)若∠BCE=30°,∠CBE=70°,求∠CFD的度数.
16.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,试判断AE与CE有怎样的数量关系?并证明你的结论.
17.如图,AC与BD相交于点O,且OA=OC,OB=OD.
(1)求证:AB∥CD;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
18.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠ABC=65°,求∠CBD的度数.
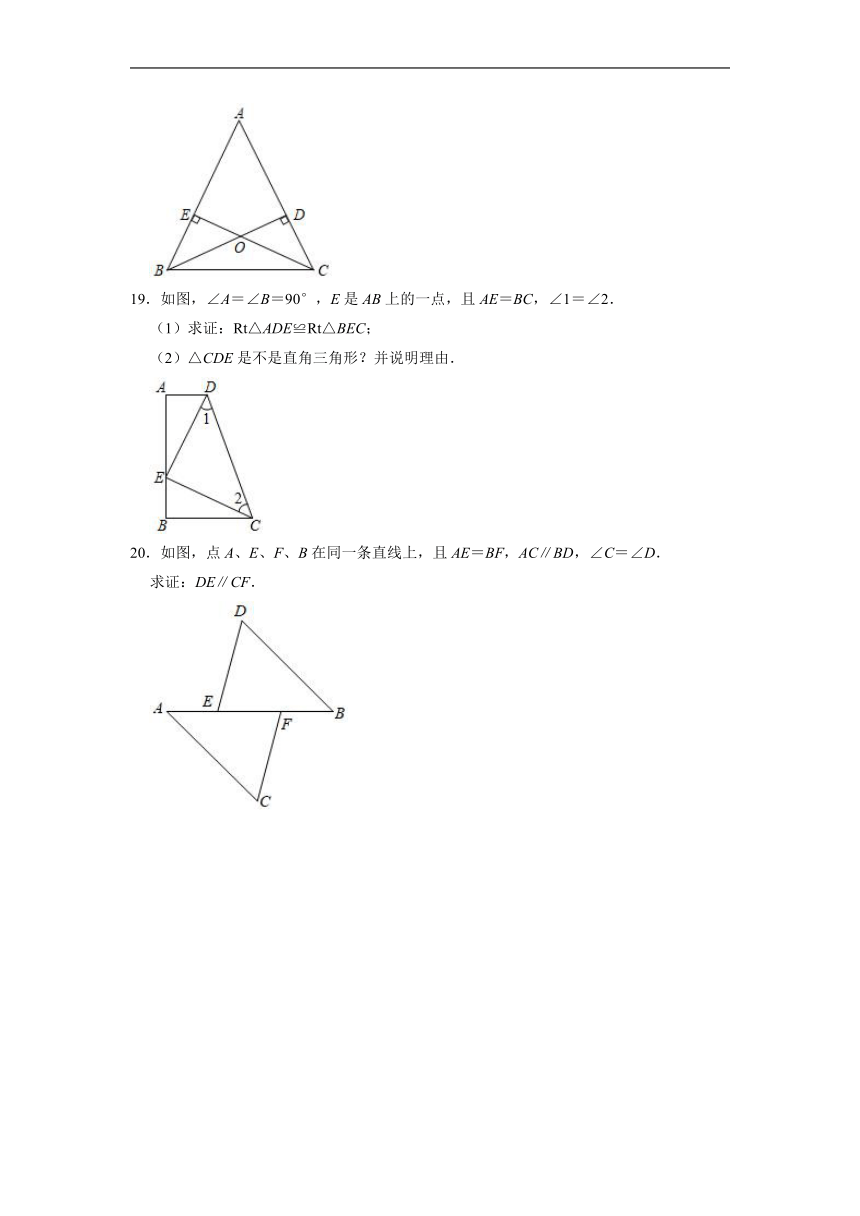
19.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:Rt△ADE≌Rt△BEC;
(2)△CDE是不是直角三角形?并说明理由.
20.如图,点A、E、F、B在同一条直线上,且AE=BF,AC∥BD,∠C=∠D.
求证:DE∥CF.
参考答案
一.选择题(共8小题,满分40分)
1.解:在△ABC和△AEF中,
,
∴△ABC≌△AEF(SAS),
∴∠C=∠AFE,
∵∠AFB=∠FAC+∠C=∠AFE+∠EFB,
∴∠BFE=∠FAC=40°,
故选:B.
2.解:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
在△ACB和△ACD中,
,
∴△ACB≌△ACD(SAS),
∴AB=AD(全等三角形的对应边相等).
故选:B.
3.解:∵∠A=∠D,AB=DE,
∴当添加∠B=∠E时,根据 ASA 判定△ABC≌△DEF;
当添加AC=DF时,根据 SAS 判定△ABC≌△DEF;
当添加∠ACD=∠BFE时,则∠ACB=∠DFE,根据 AAS 判定△ABC≌△DEF.
故选:D.
4.解:∵∠CEA=∠ADB=∠CAB=90°,
∴∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,
∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,
∴△AEC≌△BAD,
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=3+5=8.
故选:C.
5.解:A、补充∠A=∠D,可根据AAS判定△ABC≌△DCB,故A正确;
B、补充AC=DB,SSA不能判定△ABC≌△DCB,故B错误;
C、补充AB=DC,可根据SAS判定△ABC≌△DCB,故C正确;
D、补充∠ABD=∠DCA,可根据ASA判定△ABC≌△DCB,故D正确.
故选:B.
6.解:如图,在AB上截取BE=BC,连接DE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△CBD和△EBD中,
,
∴△CBD≌△EBD(SAS),
∴∠CDB=∠BDE,∠C=∠DEB,
∵∠C=2∠CDB,
∴∠CDE=∠DEB,
∴∠ADE=∠AED,
∴AD=AE,
∴△ABC的周长=AD+AE+BE+BC+CD=AB+AB+CD=27,
故选:C.
7.解:A.∵∠ABC=∠ABD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
B.∵∠BAC=∠BAD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
C.∵∠C=∠D=90°,AB=AB,AC=AD,
∴Rt△ABC≌Rt△ABD(HL),故本选项符合题意;
D.根据∠C=∠D=90°,AB=AB,AC=BC不能推出Rt△ABC≌Rt△ABD,故本选项不符合题意;
故选:C.
8.解:A、带①②去,符合ASA判定,选项符合题意;
B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故选:A.
二.填空题(共5小题,满分25分)
9.解:若添加AB=AD,且AC=AC,由“HL”可证Rt△ABC≌Rt△ADC;
若添加BC=CD,且AC=AC,由“HL”可证Rt△ABC≌Rt△ADC;
若添加∠BAC=∠DAC,且AC=AC,由“AAS”可证Rt△ABC≌Rt△ADC;
若添加∠BCA=∠DCA,且AC=AC,由“AAS”可证Rt△ABC≌Rt△ADC;
故答案为:AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD(答案不唯一).
10.证明:∵在△ABE和△DCF中,
AE⊥BC,DF⊥BC,AE=DF,AB=DC,
符合直角三角形全等条件HL,
所以△ABE≌△DCF,
故填:ABE;DCF.
11.解:∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),
∴∠BDC=∠EAC,DB=AE,①正确;
∠CBD=∠AEC,
∵∠AOB=180°﹣∠OAB﹣∠DBC,
∴∠AOB=180°﹣∠AEC﹣∠OAB=120°,③错误;
在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA),
∴AM=DN,④正确;
∠AMC=∠DNC,②正确;
CM=CN,
∵∠MCN=60°,
∴△CMN是等边三角形,⑤正确;
故答案为:①②④⑤.
12.解:在△ACO和△BCO中,
,
∴△AOC≌△BOC(SSS),
∴∠BCO=∠ACO=30°,
∴∠ACB=∠BCO+∠ACO=60°,
故答案为60°.
13.解:已知OC=OD,∠AOC=∠BOD,
添加OA=OB,利用SAS可得△AOC≌△BOD,
添加∠A=∠B,利用AAS可得△AOC≌△BOD,
添加∠C=∠D,利用ASA可得△AOC≌△BOD,
故答案为:OA=OB(或∠A=∠B或∠C=∠D).
三.解答题(共7小题,满分55分)
14.证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD与△CBD中,
,
∴△ABD≌△CBD(AAS).
15.(1)证明:∵AB∥CD,
∴∠BAE=∠FCD,
∵AF=CE,
∴AE=CF,
又∵AB=CD,
∴△ABE≌△CDF(SAS).
(2)解:∵∠BCE=30°,∠CBE=70°,
∴∠AEB=∠BCE+∠CBE=30°+70°=100°,
∵△ABE≌△CDF,
∴∠CFD=∠AEB=100°.
16.解:AE=CE,理由如下:
证明:∵FC∥AB,
∴∠ADE=∠F,(两直线平行,内错角相等)
又∵DE=FE,∠AED=∠CEF,
∴△ADE≌△CFE(ASA),
∴AE=CE.
17.(1)证明:在△OAB与△OCD中,
,
∴△OAB≌△OCD(SAS),
∴∠A=∠C,
∴AB∥CD;
(2)解:OE=OF,理由如下:
由(1)知,△OAB≌△OCD,
∴∠B=∠D,OB=OD,
在△EOB与△FOD中
,
∴△EOB≌△FOD(ASA),
∴OE=OF.
18.解:∵CE⊥AB,BD⊥AC,
∴△BCE和△CBD是直角三角形,
在Rt△BCE和Rt△CBD中,
,
∴Rt△BCE≌Rt△CBD(HL),
∴∠ABC=∠ACB,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠CBD=90°﹣∠ACB=25°.
19.(1)证明:∵∠1=∠2,
∴ED=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
,
∴Rt△ADE≌Rt△BEC(HL);
(2)解:△CDE是直角三角形,理由如下:
证明:由(1)得Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠B=90°,
∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣90°=90°,
∴△DEC为直角三角形.
20.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
∵AC∥DB,
∴∠A=∠B,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(AAS),
∴∠AFC=∠BED,
∴DE∥CF.
一.选择题(共8小题,满分40分)
1.如图,在△ABC与△AEF中,点F在BC上,AB=AE,BC=EF,∠B=∠E,AB交EF于点D,∠FAC=40°,则∠BFE=( )
A.35° B.40° C.45° D.50°
2.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS B.SAS C.ASA D.SSS
3.如图,在△ABC和△DEF中,点B、F、C、D在同条直线上,已知∠A=∠D,AB=DE,添加以下条件,不能判定△ABC≌△DEF的是( )
A.∠B=∠E B.AC=DF C.∠ACD=∠BFE D.BC=EF
4.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
5.如图,点A、D在线段BC的同侧,连接AB、AC、DB、DC,已知∠ABC=∠DCB,老师要求同学们补充一个条件使△ABC≌△DCB.以下是四个同学补充的条件,其中错误的是( )
A.∠A=∠D B.AC=DB C.AB=DC D.∠ABD=∠DCA
6.如图,在△ABC中,BD平分∠ABC,∠C=2∠CDB,AB=12,CD=3,则△ABC的周长为( )
A.21 B.24 C.27 D.30
7.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.∠ABC=∠ABD B.∠BAC=∠BAD C.AC=AD D.AC=BC
8.打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①②去 B.带②③去 C.带③④去 D.带②④去
二.填空题(共5小题,满分25分)
9.如图,AB⊥BC,AD⊥DC,垂足分别为B,D.只需添加一个条件即可证明△ABC≌△ADC,这个条件可以是 .(写出一个即可)
已知:如图,AE⊥BC,DF⊥BC,垂足分别为E,F,AE=DF,AB=DC,则△ ≌△ (HL).
11.如图,C是线段AB上的一点,△ACD和△BCE都是等边三角形,AE交CD于M,BD交CE于N,交AE于O,则①DB=AE;②∠AMC=∠DNC;③∠AOB=60°;④DN=AM;⑤△CMN是等边三角形.其中,正确的有 .
12.如图,OA=OB,AC=BC,∠ACO=30°,则∠ACB= .
13.如图,AB与CD相交于点O,OC=OD.若要得到△AOC≌△BOD,则应添加的条件是 .(写出一种情况即可)
三.解答题(共7小题,满分55分)
14.如图,已知BD平分∠ABC,∠A=∠C.
求证:△ABD≌△CBD.
15.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)若∠BCE=30°,∠CBE=70°,求∠CFD的度数.
16.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,试判断AE与CE有怎样的数量关系?并证明你的结论.
17.如图,AC与BD相交于点O,且OA=OC,OB=OD.
(1)求证:AB∥CD;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
18.如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠ABC=65°,求∠CBD的度数.
19.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:Rt△ADE≌Rt△BEC;
(2)△CDE是不是直角三角形?并说明理由.
20.如图,点A、E、F、B在同一条直线上,且AE=BF,AC∥BD,∠C=∠D.
求证:DE∥CF.
参考答案
一.选择题(共8小题,满分40分)
1.解:在△ABC和△AEF中,
,
∴△ABC≌△AEF(SAS),
∴∠C=∠AFE,
∵∠AFB=∠FAC+∠C=∠AFE+∠EFB,
∴∠BFE=∠FAC=40°,
故选:B.
2.解:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
在△ACB和△ACD中,
,
∴△ACB≌△ACD(SAS),
∴AB=AD(全等三角形的对应边相等).
故选:B.
3.解:∵∠A=∠D,AB=DE,
∴当添加∠B=∠E时,根据 ASA 判定△ABC≌△DEF;
当添加AC=DF时,根据 SAS 判定△ABC≌△DEF;
当添加∠ACD=∠BFE时,则∠ACB=∠DFE,根据 AAS 判定△ABC≌△DEF.
故选:D.
4.解:∵∠CEA=∠ADB=∠CAB=90°,
∴∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,
∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,
∴△AEC≌△BAD,
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=3+5=8.
故选:C.
5.解:A、补充∠A=∠D,可根据AAS判定△ABC≌△DCB,故A正确;
B、补充AC=DB,SSA不能判定△ABC≌△DCB,故B错误;
C、补充AB=DC,可根据SAS判定△ABC≌△DCB,故C正确;
D、补充∠ABD=∠DCA,可根据ASA判定△ABC≌△DCB,故D正确.
故选:B.
6.解:如图,在AB上截取BE=BC,连接DE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△CBD和△EBD中,
,
∴△CBD≌△EBD(SAS),
∴∠CDB=∠BDE,∠C=∠DEB,
∵∠C=2∠CDB,
∴∠CDE=∠DEB,
∴∠ADE=∠AED,
∴AD=AE,
∴△ABC的周长=AD+AE+BE+BC+CD=AB+AB+CD=27,
故选:C.
7.解:A.∵∠ABC=∠ABD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
B.∵∠BAC=∠BAD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
C.∵∠C=∠D=90°,AB=AB,AC=AD,
∴Rt△ABC≌Rt△ABD(HL),故本选项符合题意;
D.根据∠C=∠D=90°,AB=AB,AC=BC不能推出Rt△ABC≌Rt△ABD,故本选项不符合题意;
故选:C.
8.解:A、带①②去,符合ASA判定,选项符合题意;
B、带②③去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
C、带③④去,仅保留了原三角形的一个角和部分边,不符合任何判定方法,选项不符合题意;
D、带②④去,仅保留了原三角形的两个角和部分边,不符合任何判定方法,选项不符合题意;
故选:A.
二.填空题(共5小题,满分25分)
9.解:若添加AB=AD,且AC=AC,由“HL”可证Rt△ABC≌Rt△ADC;
若添加BC=CD,且AC=AC,由“HL”可证Rt△ABC≌Rt△ADC;
若添加∠BAC=∠DAC,且AC=AC,由“AAS”可证Rt△ABC≌Rt△ADC;
若添加∠BCA=∠DCA,且AC=AC,由“AAS”可证Rt△ABC≌Rt△ADC;
故答案为:AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD(答案不唯一).
10.证明:∵在△ABE和△DCF中,
AE⊥BC,DF⊥BC,AE=DF,AB=DC,
符合直角三角形全等条件HL,
所以△ABE≌△DCF,
故填:ABE;DCF.
11.解:∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),
∴∠BDC=∠EAC,DB=AE,①正确;
∠CBD=∠AEC,
∵∠AOB=180°﹣∠OAB﹣∠DBC,
∴∠AOB=180°﹣∠AEC﹣∠OAB=120°,③错误;
在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA),
∴AM=DN,④正确;
∠AMC=∠DNC,②正确;
CM=CN,
∵∠MCN=60°,
∴△CMN是等边三角形,⑤正确;
故答案为:①②④⑤.
12.解:在△ACO和△BCO中,
,
∴△AOC≌△BOC(SSS),
∴∠BCO=∠ACO=30°,
∴∠ACB=∠BCO+∠ACO=60°,
故答案为60°.
13.解:已知OC=OD,∠AOC=∠BOD,
添加OA=OB,利用SAS可得△AOC≌△BOD,
添加∠A=∠B,利用AAS可得△AOC≌△BOD,
添加∠C=∠D,利用ASA可得△AOC≌△BOD,
故答案为:OA=OB(或∠A=∠B或∠C=∠D).
三.解答题(共7小题,满分55分)
14.证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD与△CBD中,
,
∴△ABD≌△CBD(AAS).
15.(1)证明:∵AB∥CD,
∴∠BAE=∠FCD,
∵AF=CE,
∴AE=CF,
又∵AB=CD,
∴△ABE≌△CDF(SAS).
(2)解:∵∠BCE=30°,∠CBE=70°,
∴∠AEB=∠BCE+∠CBE=30°+70°=100°,
∵△ABE≌△CDF,
∴∠CFD=∠AEB=100°.
16.解:AE=CE,理由如下:
证明:∵FC∥AB,
∴∠ADE=∠F,(两直线平行,内错角相等)
又∵DE=FE,∠AED=∠CEF,
∴△ADE≌△CFE(ASA),
∴AE=CE.
17.(1)证明:在△OAB与△OCD中,
,
∴△OAB≌△OCD(SAS),
∴∠A=∠C,
∴AB∥CD;
(2)解:OE=OF,理由如下:
由(1)知,△OAB≌△OCD,
∴∠B=∠D,OB=OD,
在△EOB与△FOD中
,
∴△EOB≌△FOD(ASA),
∴OE=OF.
18.解:∵CE⊥AB,BD⊥AC,
∴△BCE和△CBD是直角三角形,
在Rt△BCE和Rt△CBD中,
,
∴Rt△BCE≌Rt△CBD(HL),
∴∠ABC=∠ACB,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠CBD=90°﹣∠ACB=25°.
19.(1)证明:∵∠1=∠2,
∴ED=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
,
∴Rt△ADE≌Rt△BEC(HL);
(2)解:△CDE是直角三角形,理由如下:
证明:由(1)得Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠B=90°,
∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣90°=90°,
∴△DEC为直角三角形.
20.证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
∵AC∥DB,
∴∠A=∠B,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(AAS),
∴∠AFC=∠BED,
∴DE∥CF.
