2022-2023学年人教版八年级数学上册12.3角的平分线的性质 同步练习题(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.3角的平分线的性质 同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 18:05:13 | ||
图片预览




文档简介
2022-2023学年人教版八年级数学上册《12.3角的平分线的性质》同步练习题(附答案)
一.选择题
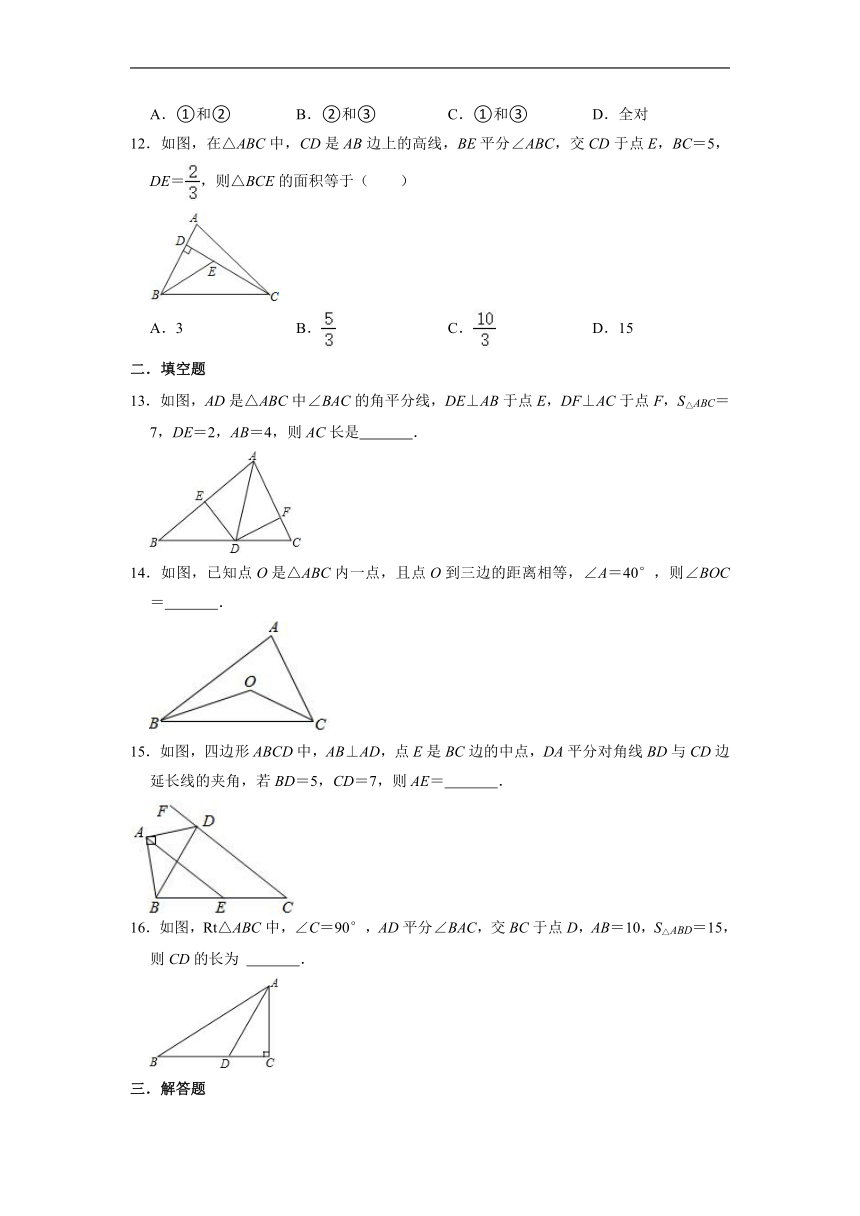
1.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积为( )
A.16 B.15 C.14 D.13
2.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC 的三条中线的交点
B.△ABC 三边的垂直平分线的交点
C.△ABC 三条角平分线的交点
D.△ABC 三条高所在直线的交点
3.下列作图语句错误的个数是( )
①以点O为圆心作弧;②延长射线OM到点A;③延长线段AB到C,使BC=AB;④过三点A,B,C作直线.
A.1个 B.2个 C.3个 D.4个
4.下列画图语句中,正确的是( )
A.画射线OP=3cm B.画出A、B两点的距离
C.延长射线OA D.连接A、B两点
5.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
A.4 B.5 C.6 D.7
6.如图,OP平分∠AOB,E为OA上一点,OE=4,P到OB的距离是2,则△OPE的面积为( )
A.2 B.3 C.4 D.8
7.如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )
A.30cm2 B.40cm2 C.50cm2 D.60cm2
8.下列作图语句正确的是( )
A.过点P作线段AB的中垂线
B.在线段AB的延长线上取一点C,使AB=BC
C.过直线a,直线b外一点P作直线MN使MN∥a∥b
D.过点P作直线AB的垂线
9.用一把带有刻度的直角尺,(1)可以画出两条平行线;(2)可以画出一个角的平分线;(3)可以确定一个圆的圆心.以上三个判断中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
10.下列关于几何画图的语句,正确的是( )
A.延长射线AB到点C,使BC=2AB
B.点P在线段AB上,点Q在直线AB的反向延长线上
C.将射线OA绕点O旋转180°,终止位置OB与起始位置OA形成平角
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b
11.如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是( )
A.①和② B.②和③ C.①和③ D.全对
12.如图,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=,则△BCE的面积等于( )
A.3 B. C. D.15
二.填空题
13.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
14.如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,则∠BOC= .
15.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
16.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为 .
三.解答题
17.如图,AC平分∠BAD,CE⊥AB,CD⊥AD,点E、D为垂足,CF=CB.
(1)求证:BE=FD;
(2)若AC=10,AD=8,求四边形ABCF的面积.
18.已知:如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
19.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5cm,∠CAD=32°,求CD的长度及∠B的度数.
20.如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB,垂足分别为E、F.
求证:CE=CF.
参考答案
一.选择题
1.解:过E作EF⊥BC于F,
∵CD是AB边上的高线,BE平分∠ABC,
∴EF=DE=3,
∵BC=10,
∴△BCE的面积为=15,
故选:B.
2.解:∵角的平分线上的点到角的两边的距离相等,
∴要使凉亭到草坪三条边的距离相等,凉亭的位置应选在△ABC 三条角平分线的交点.
故选:C.
3.解:以点O为圆心,OA为半径作弧,所以①错误;
延长线段OM到点A,所以②错误;
延长线段AB到C,使BC=AB;所以③正确;
过点A,B作直线,所以④错误.
故选:C.
4.解:A、射线OP无限长,所以A选项不符合题意;
B、量出A、B点的距离,所以B选项不符合题意;
C、射线OA不需要延长,只能反向延长射线OA,所以C选项不符合题意;
D、用直尺可以连接A、B两点,所以D选项符合题意.
故选:D.
5.解:作DF⊥AC于F,如图,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=3,
∵S△ABD+S△ACD=S△ABC,
∴×6×3+×AC×3=15,
∴AC=4.
故选:A.
6.解:如图,过P作PD⊥OB于D,作PC⊥OA于C,
∵OP是∠AOB的平分线,P到OB的距离是2,
∴PC=PD=2,
∵OE=4,
∴S△OPE=OE PC=.
故选:C.
7.解:过P作PD⊥AC于D,
∵点P是∠BAC的平分线上一点,PB⊥AB于B,
∴PD=PB=5cm,
∴S△APC=AC PD=12×5=30cm2,
故选:A.
8.解:A、只有过线段中点的垂线才叫中垂线,P是任意一点,错误;
B、应为在线段AB的延长线上取一点C,使BC=AB,错误;
C、a和b的位置不一定是平行,错误.
D、正确.
故选:D.
9.解:(1)任意画出一条直线,在直线的同旁作出两条垂线段,并且这两条垂线段相等.过这两条垂线段的另一端点画直线,与已知直线平行,正确;
(2)可先在这个角的两边量出相等的两条线段长,过这两条线段的端点向角的内部作垂线,过角的顶点和两垂线的交点的射线就是角的平分线,正确;
(3)可让直角顶点放在圆上,先得到直径,进而找到直径的中点就是圆心,正确.
故选:D.
10.解:A.延长射线AB到点C,使BC=2AB,
因为射线不能延长,
所以A选项错误,不符合题意;
B.因为直线不能反向延长,
所以B选项错误,不符合题意;
C.将射线OA绕点O旋转180°,终止位置OB与起始位置OA形成平角,C选项正确,符合题意;
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b或=a﹣b.
所以D选项错误,不符合题意.
故选:C.
11.解:连接AP,∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
∴AP是∠BAC的平分线,∠1=∠2,
∴△APR≌△APS,
∴AS=AR,
又AQ=PQ,
∴∠2=∠3,
又∠1=∠2,
∴∠1=∠3,
∴QP∥AR,
BC只是过点P,没有办法证明△BRP≌△CSP,③不成立.
故选:A.
12.解:作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=,
∴△BCE的面积=×BC×EF==.
故选:B.
二.填空题
13.解:∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=×4×2+AC 2=7,
解得AC=3.
故答案为:3.
14.解:∵∠A=40°,
∴∠ABC+∠ACB=140°,
∵点O到△ABC三边的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠OBC+∠OCB=×(∠ABC+∠ACB)=70°,
∴∠BOC=180°﹣70°=110°,
故答案为:110°.
15.解:方法一,如图,
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
方法二,如图,延长BA和CD交于一点G,
证明三角形BDA和三角形GDA全等,
得A是BG中点,
则AE是中位线,
AE等于CG的一半
故答案为:6.
16.解:如图,过点D作DE⊥AB于点E;
∵∠C=90°,AD平分∠BAC,
∴CD=DE;
∵,且AB=10,
∴DE=3,CD=DE=3.
故答案为3.
三.解答题
17.(1)证明:∵AC平分∠BAD,CE⊥AB,CD⊥AD,
∴CD=CE,
在Rt△CBE和Rt△CFD中,
,
∴Rt△CBE≌Rt△CFD(HL),
∴BE=FD;
(2)解:在Rt△ACD中,
∵AC=10,AD=8,
∴CD=6,
∵AC=AC,CD=CE,
∴Rt△ACD≌Rt△ACE(HL),
∴S△ACD=S△ACE,
∵Rt△CBE≌Rt△CFD,
∴S△CBE=S△CFD,
∴四边形ABCF的面积=S四边形AECD=2S△ACD=2××6×8=48.
18.证明:在Rt△PFD和Rt△PGE中,,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE,
∵P是OC上一点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
19.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE=5cm,
又∵AD平分∠BAC,
∴∠BAC=2∠CAD=2×32°=64°,
∴∠B=90°﹣∠BAC=90°﹣64°=26°.
20.证明:连接AC,
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS).
∴∠DAC=∠BAC.
又∵CE⊥AD,CF⊥AB,
∴CE=CF(角平分线上的点到角两边的距离相等).
一.选择题
1.如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=10,DE=3,则△BCE的面积为( )
A.16 B.15 C.14 D.13
2.如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC 的三条中线的交点
B.△ABC 三边的垂直平分线的交点
C.△ABC 三条角平分线的交点
D.△ABC 三条高所在直线的交点
3.下列作图语句错误的个数是( )
①以点O为圆心作弧;②延长射线OM到点A;③延长线段AB到C,使BC=AB;④过三点A,B,C作直线.
A.1个 B.2个 C.3个 D.4个
4.下列画图语句中,正确的是( )
A.画射线OP=3cm B.画出A、B两点的距离
C.延长射线OA D.连接A、B两点
5.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
A.4 B.5 C.6 D.7
6.如图,OP平分∠AOB,E为OA上一点,OE=4,P到OB的距离是2,则△OPE的面积为( )
A.2 B.3 C.4 D.8
7.如图,点P是∠BAC的平分线上一点,PB⊥AB于B,且PB=5cm,AC=12,则△APC的面积是( )
A.30cm2 B.40cm2 C.50cm2 D.60cm2
8.下列作图语句正确的是( )
A.过点P作线段AB的中垂线
B.在线段AB的延长线上取一点C,使AB=BC
C.过直线a,直线b外一点P作直线MN使MN∥a∥b
D.过点P作直线AB的垂线
9.用一把带有刻度的直角尺,(1)可以画出两条平行线;(2)可以画出一个角的平分线;(3)可以确定一个圆的圆心.以上三个判断中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
10.下列关于几何画图的语句,正确的是( )
A.延长射线AB到点C,使BC=2AB
B.点P在线段AB上,点Q在直线AB的反向延长线上
C.将射线OA绕点O旋转180°,终止位置OB与起始位置OA形成平角
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b
11.如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是( )
A.①和② B.②和③ C.①和③ D.全对
12.如图,在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=,则△BCE的面积等于( )
A.3 B. C. D.15
二.填空题
13.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC长是 .
14.如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,则∠BOC= .
15.如图,四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= .
16.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为 .
三.解答题
17.如图,AC平分∠BAD,CE⊥AB,CD⊥AD,点E、D为垂足,CF=CB.
(1)求证:BE=FD;
(2)若AC=10,AD=8,求四边形ABCF的面积.
18.已知:如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F、G分别是OA、OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
19.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,如果DE=5cm,∠CAD=32°,求CD的长度及∠B的度数.
20.如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB,垂足分别为E、F.
求证:CE=CF.
参考答案
一.选择题
1.解:过E作EF⊥BC于F,
∵CD是AB边上的高线,BE平分∠ABC,
∴EF=DE=3,
∵BC=10,
∴△BCE的面积为=15,
故选:B.
2.解:∵角的平分线上的点到角的两边的距离相等,
∴要使凉亭到草坪三条边的距离相等,凉亭的位置应选在△ABC 三条角平分线的交点.
故选:C.
3.解:以点O为圆心,OA为半径作弧,所以①错误;
延长线段OM到点A,所以②错误;
延长线段AB到C,使BC=AB;所以③正确;
过点A,B作直线,所以④错误.
故选:C.
4.解:A、射线OP无限长,所以A选项不符合题意;
B、量出A、B点的距离,所以B选项不符合题意;
C、射线OA不需要延长,只能反向延长射线OA,所以C选项不符合题意;
D、用直尺可以连接A、B两点,所以D选项符合题意.
故选:D.
5.解:作DF⊥AC于F,如图,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF=3,
∵S△ABD+S△ACD=S△ABC,
∴×6×3+×AC×3=15,
∴AC=4.
故选:A.
6.解:如图,过P作PD⊥OB于D,作PC⊥OA于C,
∵OP是∠AOB的平分线,P到OB的距离是2,
∴PC=PD=2,
∵OE=4,
∴S△OPE=OE PC=.
故选:C.
7.解:过P作PD⊥AC于D,
∵点P是∠BAC的平分线上一点,PB⊥AB于B,
∴PD=PB=5cm,
∴S△APC=AC PD=12×5=30cm2,
故选:A.
8.解:A、只有过线段中点的垂线才叫中垂线,P是任意一点,错误;
B、应为在线段AB的延长线上取一点C,使BC=AB,错误;
C、a和b的位置不一定是平行,错误.
D、正确.
故选:D.
9.解:(1)任意画出一条直线,在直线的同旁作出两条垂线段,并且这两条垂线段相等.过这两条垂线段的另一端点画直线,与已知直线平行,正确;
(2)可先在这个角的两边量出相等的两条线段长,过这两条线段的端点向角的内部作垂线,过角的顶点和两垂线的交点的射线就是角的平分线,正确;
(3)可让直角顶点放在圆上,先得到直径,进而找到直径的中点就是圆心,正确.
故选:D.
10.解:A.延长射线AB到点C,使BC=2AB,
因为射线不能延长,
所以A选项错误,不符合题意;
B.因为直线不能反向延长,
所以B选项错误,不符合题意;
C.将射线OA绕点O旋转180°,终止位置OB与起始位置OA形成平角,C选项正确,符合题意;
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b或=a﹣b.
所以D选项错误,不符合题意.
故选:C.
11.解:连接AP,∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
∴AP是∠BAC的平分线,∠1=∠2,
∴△APR≌△APS,
∴AS=AR,
又AQ=PQ,
∴∠2=∠3,
又∠1=∠2,
∴∠1=∠3,
∴QP∥AR,
BC只是过点P,没有办法证明△BRP≌△CSP,③不成立.
故选:A.
12.解:作EF⊥BC于F,
∵BE平分∠ABC,EF⊥BC,ED⊥AB,
∴EF=DE=,
∴△BCE的面积=×BC×EF==.
故选:B.
二.填空题
13.解:∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=×4×2+AC 2=7,
解得AC=3.
故答案为:3.
14.解:∵∠A=40°,
∴∠ABC+∠ACB=140°,
∵点O到△ABC三边的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠OBC+∠OCB=×(∠ABC+∠ACB)=70°,
∴∠BOC=180°﹣70°=110°,
故答案为:110°.
15.解:方法一,如图,
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
方法二,如图,延长BA和CD交于一点G,
证明三角形BDA和三角形GDA全等,
得A是BG中点,
则AE是中位线,
AE等于CG的一半
故答案为:6.
16.解:如图,过点D作DE⊥AB于点E;
∵∠C=90°,AD平分∠BAC,
∴CD=DE;
∵,且AB=10,
∴DE=3,CD=DE=3.
故答案为3.
三.解答题
17.(1)证明:∵AC平分∠BAD,CE⊥AB,CD⊥AD,
∴CD=CE,
在Rt△CBE和Rt△CFD中,
,
∴Rt△CBE≌Rt△CFD(HL),
∴BE=FD;
(2)解:在Rt△ACD中,
∵AC=10,AD=8,
∴CD=6,
∵AC=AC,CD=CE,
∴Rt△ACD≌Rt△ACE(HL),
∴S△ACD=S△ACE,
∵Rt△CBE≌Rt△CFD,
∴S△CBE=S△CFD,
∴四边形ABCF的面积=S四边形AECD=2S△ACD=2××6×8=48.
18.证明:在Rt△PFD和Rt△PGE中,,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE,
∵P是OC上一点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
19.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE=5cm,
又∵AD平分∠BAC,
∴∠BAC=2∠CAD=2×32°=64°,
∴∠B=90°﹣∠BAC=90°﹣64°=26°.
20.证明:连接AC,
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC(SSS).
∴∠DAC=∠BAC.
又∵CE⊥AD,CF⊥AB,
∴CE=CF(角平分线上的点到角两边的距离相等).
