新人教A版必修第二册9.2.1总体取值规律的估计课件(共36张PPT)
文档属性
| 名称 | 新人教A版必修第二册9.2.1总体取值规律的估计课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 08:57:55 | ||
图片预览










文档简介
(共36张PPT)
9.2 用样本估计总体
9.2.1 总体取值规律的估计
明确目标 发展素养
1.选择适当的统计图表对数据进行可视化描述. 2.结合实例,理解并掌握统计图表的画法及应用,能用样本估计总体的取值规律. 1.通过对统计图表的学习,培养数学抽象、直观想象素养.
2.通过应用统计图表估计总体的取值规律,培养数据分析素养.
极差为一组数据中________________的差.
第二步,决定组距与组数.
第三步,将数据分组.
通常对组内数据取”__________区间,最后一组数据取闭区间.
最大值与最小值
左闭右开
(二)基本知能小试
1.判断正误:
(1)用样本的频率分布可以估计总体分布. ( )
(2)频率分布直方图的纵轴表示频率. ( )
(3)频率分布直方图中小矩形的面积表示该组的个体数. ( )
2.一个容量为80的样本中,数据的最大值为152,最小值为60,组距为10,应将样本数据分为 ( )
A.10组 B.9组
C.8组 D.7组
√
×
×
答案:A
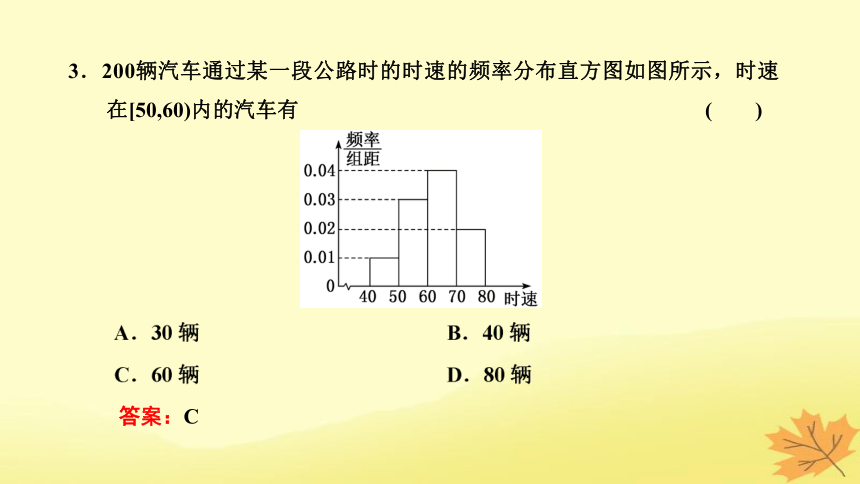
3.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,时速在[50,60)内的汽车有 ( )
答案:C
知识点二 其他几类常用的统计图
(一)教材梳理填空
统计图表 主要应用
扇形图 直观描述各类数据占总数的______
条形图和 直方图 直观描述不同类别或分组数据的____________
折线图 描述数据随______的变化趋势
比例
频数和频率
时间
(二)基本知能小试
1.判断正误:
(1)解决统计类问题时常需要将若干种统计图结合,不能孤立分开.( )
(2)扇形统计图表示的是比例,条形统计图不表示比例. ( )
2.把过期的药品随意丢弃,会造成对土壤和水体的污染,危害人们的健康.如何处理过期药品,有关机构随机对若干家庭进行调查,调查结果如图,其中对过期药品处理不正确的家庭达到 ( )
答案:D
3.某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球4项活动的参加人数做了统计,绘制了条形统计图(如图所示),那么参加羽毛球活动的人数的频率是________.
答案:0.1
[探究发现]
(1)要做频率分布表,需要对原始数据做哪些工作?
提示:分组、频数累计、计算频数和频率.
(2)画频率分布直方图时,如何决定组数与组距?
(3)同一组数据,如果组距不同,得到的频率分布直方图也会不同吗?
提示:不同.对于同一组数据分析时,要选好组距和组数,不同的组距与组数对结果有一定的影响.为了方便,往往按等距分组,或者除了第一和最后的两段,其他各段按等距分组.
【学透用活】
[典例1] 某中学从高一年级随机抽取50名学生进行智力测验,其得分如下(单位:分):
48 64 52 86 71 48 64 41 86 79
71 68 82 84 68 64 62 68 81 57
90 52 74 73 56 78 47 66 55 64
56 88 69 40 73 97 68 56 67 59
70 52 79 44 55 69 62 58 32 58
根据上面的数据,回答下列问题:
(1)这次测验成绩的最高分和最低分分别是多少?
(2)将区间[30,100]平均分成7个小区间,试列出这50名学生智力测验成绩的频率分布表,进而画出频率分布直方图.
(3)分析频率分布直方图,你能得出什么结论?
[解] (1)这次测验成绩的最低分是32分,最高分是97分.
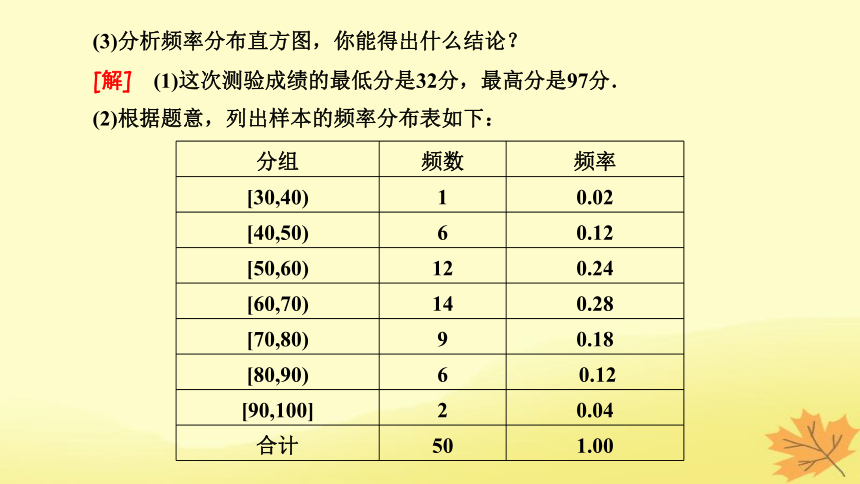
(2)根据题意,列出样本的频率分布表如下:
分组 频数 频率
[30,40) 1 0.02
[40,50) 6 0.12
[50,60) 12 0.24
[60,70) 14 0.28
[70,80) 9 0.18
[80,90) 6 0.12
[90,100] 2 0.04
合计 50 1.00
频率分布直方图如图所示:
【对点练清】
如表所示给出了在某校500名12岁男孩中,用随机抽样得出的120人的身高(单位:cm).
区间 界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间 界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计身高小于134 cm的人数占总人数的百分比.
解:(1)样本频率分布表如下:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
分组 频数 频率
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
(2)其频率分布直方图如下:
(3)由样本频率分布表可知,身高小于134 cm的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134 cm的人数占总人数的19%.
题型二 频率分布直方图的应用
【学透用活】
[典例2] 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,则该校全体高一年级学生的达标率是多少?
【对点练清】
1.某高校调查了200名学生每周的自习时间(单位:时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是 ( )
答案:D
2.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50~350千瓦时范围内,频率分布直方图如图所示.
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2018年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比 较平稳
[解析] 由2018年1月至2020年12月期间月接待游客量的折线图得:在A中,年接待游客量虽然逐月波动,但总体上逐年增加,故A正确;在B中,各年的月接待游客量高峰期都在8月,故B正确;在C中,2018年1月至12月月接待游客量的中位数小于30万人,故C错误;在D中,各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确.故选C.
[答案] C
【对点练清】
1.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下扇形统计图:
则下面结论中不正确的是 ( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
答案:A
答案:甲
分组 频数 频率
0≤t<5 0 0
5≤t<10 10 0.10
10≤t<15 10 ②
15≤t<20 ① 0.50
20≤t≤25 30 0.30
合计 100 1.00
答案:C
9.2 用样本估计总体
9.2.1 总体取值规律的估计
明确目标 发展素养
1.选择适当的统计图表对数据进行可视化描述. 2.结合实例,理解并掌握统计图表的画法及应用,能用样本估计总体的取值规律. 1.通过对统计图表的学习,培养数学抽象、直观想象素养.
2.通过应用统计图表估计总体的取值规律,培养数据分析素养.
极差为一组数据中________________的差.
第二步,决定组距与组数.
第三步,将数据分组.
通常对组内数据取”__________区间,最后一组数据取闭区间.
最大值与最小值
左闭右开
(二)基本知能小试
1.判断正误:
(1)用样本的频率分布可以估计总体分布. ( )
(2)频率分布直方图的纵轴表示频率. ( )
(3)频率分布直方图中小矩形的面积表示该组的个体数. ( )
2.一个容量为80的样本中,数据的最大值为152,最小值为60,组距为10,应将样本数据分为 ( )
A.10组 B.9组
C.8组 D.7组
√
×
×
答案:A
3.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,时速在[50,60)内的汽车有 ( )
答案:C
知识点二 其他几类常用的统计图
(一)教材梳理填空
统计图表 主要应用
扇形图 直观描述各类数据占总数的______
条形图和 直方图 直观描述不同类别或分组数据的____________
折线图 描述数据随______的变化趋势
比例
频数和频率
时间
(二)基本知能小试
1.判断正误:
(1)解决统计类问题时常需要将若干种统计图结合,不能孤立分开.( )
(2)扇形统计图表示的是比例,条形统计图不表示比例. ( )
2.把过期的药品随意丢弃,会造成对土壤和水体的污染,危害人们的健康.如何处理过期药品,有关机构随机对若干家庭进行调查,调查结果如图,其中对过期药品处理不正确的家庭达到 ( )
答案:D
3.某班计划开展一些课外活动,全班有40名学生报名参加,他们就乒乓球、足球、跳绳、羽毛球4项活动的参加人数做了统计,绘制了条形统计图(如图所示),那么参加羽毛球活动的人数的频率是________.
答案:0.1
[探究发现]
(1)要做频率分布表,需要对原始数据做哪些工作?
提示:分组、频数累计、计算频数和频率.
(2)画频率分布直方图时,如何决定组数与组距?
(3)同一组数据,如果组距不同,得到的频率分布直方图也会不同吗?
提示:不同.对于同一组数据分析时,要选好组距和组数,不同的组距与组数对结果有一定的影响.为了方便,往往按等距分组,或者除了第一和最后的两段,其他各段按等距分组.
【学透用活】
[典例1] 某中学从高一年级随机抽取50名学生进行智力测验,其得分如下(单位:分):
48 64 52 86 71 48 64 41 86 79
71 68 82 84 68 64 62 68 81 57
90 52 74 73 56 78 47 66 55 64
56 88 69 40 73 97 68 56 67 59
70 52 79 44 55 69 62 58 32 58
根据上面的数据,回答下列问题:
(1)这次测验成绩的最高分和最低分分别是多少?
(2)将区间[30,100]平均分成7个小区间,试列出这50名学生智力测验成绩的频率分布表,进而画出频率分布直方图.
(3)分析频率分布直方图,你能得出什么结论?
[解] (1)这次测验成绩的最低分是32分,最高分是97分.
(2)根据题意,列出样本的频率分布表如下:
分组 频数 频率
[30,40) 1 0.02
[40,50) 6 0.12
[50,60) 12 0.24
[60,70) 14 0.28
[70,80) 9 0.18
[80,90) 6 0.12
[90,100] 2 0.04
合计 50 1.00
频率分布直方图如图所示:
【对点练清】
如表所示给出了在某校500名12岁男孩中,用随机抽样得出的120人的身高(单位:cm).
区间 界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间 界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
(1)列出样本频率分布表;
(2)画出频率分布直方图;
(3)估计身高小于134 cm的人数占总人数的百分比.
解:(1)样本频率分布表如下:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
分组 频数 频率
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
(2)其频率分布直方图如下:
(3)由样本频率分布表可知,身高小于134 cm的男孩出现的频率为0.04+0.07+0.08=0.19,所以我们估计身高小于134 cm的人数占总人数的19%.
题型二 频率分布直方图的应用
【学透用活】
[典例2] 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,则该校全体高一年级学生的达标率是多少?
【对点练清】
1.某高校调查了200名学生每周的自习时间(单位:时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是 ( )
答案:D
2.从某小区抽取100户居民进行月用电量调查,发现其用电量都在50~350千瓦时范围内,频率分布直方图如图所示.
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2018年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比 较平稳
[解析] 由2018年1月至2020年12月期间月接待游客量的折线图得:在A中,年接待游客量虽然逐月波动,但总体上逐年增加,故A正确;在B中,各年的月接待游客量高峰期都在8月,故B正确;在C中,2018年1月至12月月接待游客量的中位数小于30万人,故C错误;在D中,各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确.故选C.
[答案] C
【对点练清】
1.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下扇形统计图:
则下面结论中不正确的是 ( )
A.新农村建设后,种植收入减少
B.新农村建设后,其他收入增加了一倍以上
C.新农村建设后,养殖收入增加了一倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
答案:A
答案:甲
分组 频数 频率
0≤t<5 0 0
5≤t<10 10 0.10
10≤t<15 10 ②
15≤t<20 ① 0.50
20≤t≤25 30 0.30
合计 100 1.00
答案:C
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
