新人教A版必修第二册8.5.3平面与平面平行课件(共29张PPT)
文档属性
| 名称 | 新人教A版必修第二册8.5.3平面与平面平行课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:05:12 | ||
图片预览








文档简介
(共29张PPT)
8.5.3 平面与平面平行
明确目标 发展素养
1.借助长方体,通过直观感知,了解空间中平面与平面的位置关系. 2.归纳出平面与平面平行的判定定理、性质定理,并加以证明. 3.能用已获得的结论证明空间基本图形位置关系的简单命题. 在发现、推导和应用平面与平面平行的判定定理、性质定理的过程中,培养数学抽象、直观想象和逻辑推理素养.
两条相交直线
a β,b β,a∩b=P,a∥α,b∥α
平行
[微思考] 如果一个平面内的两条相交直线与另一个平面内的两条相交直线分别对应平行,那么这两个平面平行吗?
提示:平行.
×
√
√
√
2.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是 ( )
A.一定平行 B.一定相交
C.平行或相交 D.以上判断都不对
答案:C
3.已知直线a∥平面α,平面α∥平面β,则a与β的位置关系为__________.
答案:a β或a∥β
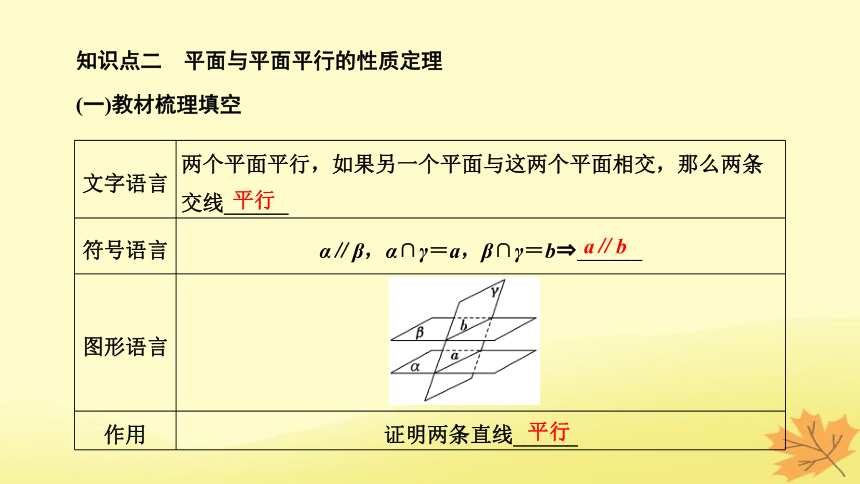
知识点二 平面与平面平行的性质定理
(一)教材梳理填空
文字语言 两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______
符号语言 α∥β,α∩γ=a,β∩γ=b ______
图形语言
作用 证明两条直线______
平行
a∥b
平行
[微思考] 两个平面平行,那么两个平面内的所有直线都相互平行吗?
提示:不一定.因为两个平面平行,所以分别在这两个平面内的任两条直线无公共点,它们平行或异面.
答案:A
×
√
√
答案:D
[方法技巧]
应用平面与平面平行的性质定理的基本步骤
答案:C
、
[方法技巧]
解决平行关系的综合问题的策略
(1)在遇到线面平行时,常需作(或找)出过已知直线与已知平面相交的辅助平面,以便运用线面平行的性质.
(2)线线平行、线面平行、面面平行是一个有机的整体,要灵活应用,实现相互联系、相互转化.在解决立体几何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.
分析以上解题过程是否正确,若错误请指出错因,并给出正确的解题过程.
提示:学生在解答中盲目地认为E,B,F,D1四点共面,但由已知条件并不能说明这四点共面,同时条件AE=C1F也没有用到.
二、应用性——强调学以致用
2.高鹏同学家购买了一套新房,为了充分利用自己的房间,他想靠墙角设计一个双层床,上层摆放自己的玩具等物品,但装修师傅却问道:我怎样装修才能使双层床的各层面与地面平行呢?大家想想,装修师傅应该怎样装修?
8.5.3 平面与平面平行
明确目标 发展素养
1.借助长方体,通过直观感知,了解空间中平面与平面的位置关系. 2.归纳出平面与平面平行的判定定理、性质定理,并加以证明. 3.能用已获得的结论证明空间基本图形位置关系的简单命题. 在发现、推导和应用平面与平面平行的判定定理、性质定理的过程中,培养数学抽象、直观想象和逻辑推理素养.
两条相交直线
a β,b β,a∩b=P,a∥α,b∥α
平行
[微思考] 如果一个平面内的两条相交直线与另一个平面内的两条相交直线分别对应平行,那么这两个平面平行吗?
提示:平行.
×
√
√
√
2.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是 ( )
A.一定平行 B.一定相交
C.平行或相交 D.以上判断都不对
答案:C
3.已知直线a∥平面α,平面α∥平面β,则a与β的位置关系为__________.
答案:a β或a∥β
知识点二 平面与平面平行的性质定理
(一)教材梳理填空
文字语言 两个平面平行,如果另一个平面与这两个平面相交,那么两条交线______
符号语言 α∥β,α∩γ=a,β∩γ=b ______
图形语言
作用 证明两条直线______
平行
a∥b
平行
[微思考] 两个平面平行,那么两个平面内的所有直线都相互平行吗?
提示:不一定.因为两个平面平行,所以分别在这两个平面内的任两条直线无公共点,它们平行或异面.
答案:A
×
√
√
答案:D
[方法技巧]
应用平面与平面平行的性质定理的基本步骤
答案:C
、
[方法技巧]
解决平行关系的综合问题的策略
(1)在遇到线面平行时,常需作(或找)出过已知直线与已知平面相交的辅助平面,以便运用线面平行的性质.
(2)线线平行、线面平行、面面平行是一个有机的整体,要灵活应用,实现相互联系、相互转化.在解决立体几何中的平行问题时,一般都要用到平行关系的转化.转化思想是解决这类问题的最有效的方法.
分析以上解题过程是否正确,若错误请指出错因,并给出正确的解题过程.
提示:学生在解答中盲目地认为E,B,F,D1四点共面,但由已知条件并不能说明这四点共面,同时条件AE=C1F也没有用到.
二、应用性——强调学以致用
2.高鹏同学家购买了一套新房,为了充分利用自己的房间,他想靠墙角设计一个双层床,上层摆放自己的玩具等物品,但装修师傅却问道:我怎样装修才能使双层床的各层面与地面平行呢?大家想想,装修师傅应该怎样装修?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
