2.3 二次函数与一元二次方程、不等式课件(共47张)
文档属性
| 名称 | 2.3 二次函数与一元二次方程、不等式课件(共47张) |  | |
| 格式 | pptx | ||
| 文件大小 | 940.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:04:14 | ||
图片预览











文档简介
(共47张PPT)
第二章 一元二次函数、方程和不等式
2.3 二次函数与一元二次方程、不等式
学习目标 素养要求
1.会结合一元二次函数的图象,判断一元二次方程实根的存在性及实根个数,了解函数零点与方程根的关系 逻辑推理
2.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集 直观想象
3.借助一元二次函数的图象,了解一元二次不等式与相应函数、方程的联系 数学运算
| 自 学 导 引 |
1.只含有________未知数,并且未知数的最高次数是________的不等式,称为一元二次不等式.
2.一元二次不等式的一般形式
(1)ax2+bx+c>0(a≠0).
(2)ax2+bx+c≥0(a≠0).
(3)ax2+bx+c<0(a≠0).
(4)ax2+bx+c≤0(a≠0).
一个
一元二次不等式的概念
2
不等式x2-y2>0是一元二次不等式吗?
【提示】此不等式含有两个变量,根据一元二次不等式的定义,可知不是一元二次不等式.
使一元二次不等式成立的未知数的值,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的________.
解集
一元二次不等式的解与解集
类比“方程x2=1的解集是{1,-1},解集中的每一个元素均可使等式成立”.不等式x2>1的解集及其含义是什么?
【提示】不等式x2>1的解集为{x|x<-1或x>1},该集合中每一个元素都是不等式的解,即不等式的每一个解均使不等式成立.
对于二次函数y=ax2+bx+c,把使ax2+bx+c=0的实数x叫做二次函数y=ax2+bx+c的零点.
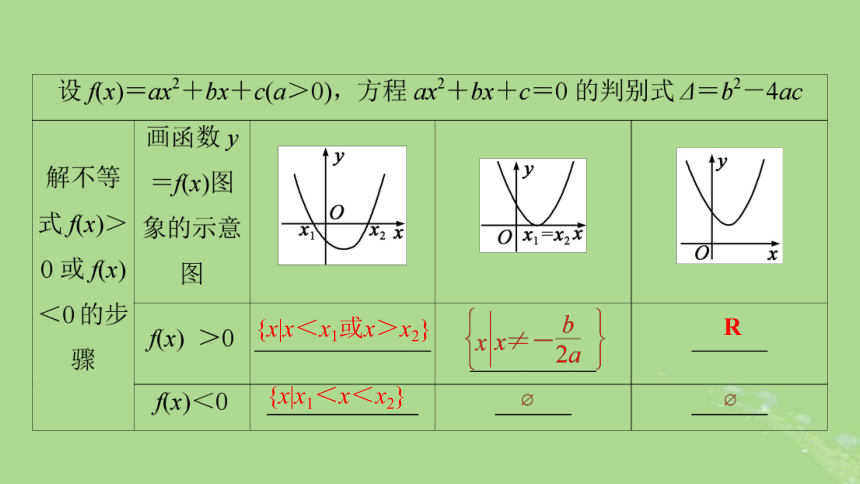
三个“二次”的关系
{x|x<x1或x>x2}
R
{x|x1<x<x2}
【预习自测】
若一元二次不等式ax2+x-1>0的解集为R,则实数a应满足什么条件?
| 课 堂 互 动 |
题型1 不含参数的一元二次不等式的解法
素养点睛:考查数学运算和逻辑推理的核心素养.
(3)原不等式可化为2x2-3x+2>0,
因为Δ=9-4×2×2=-7<0,
所以方程2x2-3x+2=0无实根.
又二次函数y=2x2-3x+2的图象开口向上,
所以原不等式的解集为R.
解不含参数的一元二次不等式的一般步骤
(1)标准化:通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
(2)判别式:对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求实根:求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画草图:根据一元二次方程根的情况画出对应的二次函数图象的草图.
(5)写解集:根据图象写出不等式的解集.
1.解下列不等式:
(1)2x2-3x-2>0;
(2)x2-4x+4>0;
(3)-x2+2x-3<0;
(4)-3x2+5x-2>0.
解关于x的不等式ax2-(a+1)x+1<0.
素养点睛:考查数学运算和逻辑推理的核心素养.
题型2 含参数的一元二次不等式的解法
解含参数的一元二次不等式的一般步骤
注:对参数分类讨论的每一种情况是相互独立的一元二次不等式的解集,不能合并.
2.解关于x的不等式2x2+ax+2>0.
已知关于x的不等式ax2+bx+c>0的解集为{x|2素养点睛:考查数学运算和逻辑推理的核心素养.
题型3 三个“二次”之间的关系
已知以a,b,c为参数的不等式(如ax2+bx+c>0)的解集,求解其他不等式的解集时,一般遵循:
(1)根据解集来判断二次项系数的符号.
(2)根据根与系数的关系把b,c用a表示出来并代入所要解的不等式.
(3)将不等式化为具体的一元二次不等式求解.
某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x(0(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年度有所增加,问投入成本增加的比例x应在什么范围内?
素养点睛:考查数学建模和数学运算的核心素养.
题型4 一元二次不等式的实际应用
解不等式应用题的步骤
4.某校园内有一块长为800 m,宽为600 m的长方形地面,现要对该地面进行绿化,规划四周种花卉(花卉带的宽度相同),中间种草坪,若要求草坪的面积不小于总面积的一半,求花卉带宽度的范围.
易错警示 不等式变形前后不同解
| 素 养 达 成 |
1.解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集(体现了直观想象的核心素养).
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m若(x-m)(x-n)<0,则可得{x|m<x<n}.
有口诀如下:大于取两边,小于取中间.
2.含参数的一元二次型的不等式
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”(体现了数学运算和逻辑推理的核心素养),讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1<x2.
3.由一元二次不等式的解集可以逆推二次函数的零点及图象的开口方向.
【答案】B
【解析】因为2x+3-x2>0,所以x2-2x-3<0,方程x2-2x-3=0的根为-1,3,所以不等式的解集为{x|-1<x<3}.故选B.
2.(题型4)用一根长为100 m的绳子围成一个面积大于600 m2的矩形,设围成的矩形一边的长为x m,则x的取值范围为 ( )
A.{x|15<x<25} B.{x|20<x<30}
C.{x|25<x<35} D.{x|30<x<40}
【答案】B
【解析】设围成的矩形一边的长为x m,则另一边的长为(50-x) m,且0<x<50.由题意,得围成矩形的面积S=x(50-x)>600,即x2-50x+600<0,解得20<x<30.
4.(题型3)(2020年枣庄高一期中)已知关于x的不等式x2-5ax+b>0的解集为{x|x<1或x>4},则a+b=________.
【答案】5
【解析】根据不等式x2-5ax+b>0的解集为{x|x<1或x>4},知方程x2-5ax+b=0的两个根是1和4,则5a=1+4,b=1×4,解得a=1,b=4.所以a+b=5.
5.(题型1)解下列不等式:
(1)x(7-x)≥12;
(2)x2>2(x-1).
解:(1)原不等式可化为x2-7x+12≤0,
因为方程x2-7x+12=0的两根为x1=3,x2=4,
所以原不等式的解集为{x|3≤x≤4}.
(2)原不等式可以化为x2-2x+2>0,
因为判别式Δ=4-8=-4<0,
所以方程x2-2x+2=0无实根,而抛物线y=x2-2x+2开口向上,
所以原不等式的解集为R.
第二章 一元二次函数、方程和不等式
2.3 二次函数与一元二次方程、不等式
学习目标 素养要求
1.会结合一元二次函数的图象,判断一元二次方程实根的存在性及实根个数,了解函数零点与方程根的关系 逻辑推理
2.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集 直观想象
3.借助一元二次函数的图象,了解一元二次不等式与相应函数、方程的联系 数学运算
| 自 学 导 引 |
1.只含有________未知数,并且未知数的最高次数是________的不等式,称为一元二次不等式.
2.一元二次不等式的一般形式
(1)ax2+bx+c>0(a≠0).
(2)ax2+bx+c≥0(a≠0).
(3)ax2+bx+c<0(a≠0).
(4)ax2+bx+c≤0(a≠0).
一个
一元二次不等式的概念
2
不等式x2-y2>0是一元二次不等式吗?
【提示】此不等式含有两个变量,根据一元二次不等式的定义,可知不是一元二次不等式.
使一元二次不等式成立的未知数的值,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的________.
解集
一元二次不等式的解与解集
类比“方程x2=1的解集是{1,-1},解集中的每一个元素均可使等式成立”.不等式x2>1的解集及其含义是什么?
【提示】不等式x2>1的解集为{x|x<-1或x>1},该集合中每一个元素都是不等式的解,即不等式的每一个解均使不等式成立.
对于二次函数y=ax2+bx+c,把使ax2+bx+c=0的实数x叫做二次函数y=ax2+bx+c的零点.
三个“二次”的关系
{x|x<x1或x>x2}
R
{x|x1<x<x2}
【预习自测】
若一元二次不等式ax2+x-1>0的解集为R,则实数a应满足什么条件?
| 课 堂 互 动 |
题型1 不含参数的一元二次不等式的解法
素养点睛:考查数学运算和逻辑推理的核心素养.
(3)原不等式可化为2x2-3x+2>0,
因为Δ=9-4×2×2=-7<0,
所以方程2x2-3x+2=0无实根.
又二次函数y=2x2-3x+2的图象开口向上,
所以原不等式的解集为R.
解不含参数的一元二次不等式的一般步骤
(1)标准化:通过对不等式的变形,使不等式右侧为0,使二次项系数为正.
(2)判别式:对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求实根:求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画草图:根据一元二次方程根的情况画出对应的二次函数图象的草图.
(5)写解集:根据图象写出不等式的解集.
1.解下列不等式:
(1)2x2-3x-2>0;
(2)x2-4x+4>0;
(3)-x2+2x-3<0;
(4)-3x2+5x-2>0.
解关于x的不等式ax2-(a+1)x+1<0.
素养点睛:考查数学运算和逻辑推理的核心素养.
题型2 含参数的一元二次不等式的解法
解含参数的一元二次不等式的一般步骤
注:对参数分类讨论的每一种情况是相互独立的一元二次不等式的解集,不能合并.
2.解关于x的不等式2x2+ax+2>0.
已知关于x的不等式ax2+bx+c>0的解集为{x|2
题型3 三个“二次”之间的关系
已知以a,b,c为参数的不等式(如ax2+bx+c>0)的解集,求解其他不等式的解集时,一般遵循:
(1)根据解集来判断二次项系数的符号.
(2)根据根与系数的关系把b,c用a表示出来并代入所要解的不等式.
(3)将不等式化为具体的一元二次不等式求解.
某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x(0
(2)为使本年度的年利润比上年度有所增加,问投入成本增加的比例x应在什么范围内?
素养点睛:考查数学建模和数学运算的核心素养.
题型4 一元二次不等式的实际应用
解不等式应用题的步骤
4.某校园内有一块长为800 m,宽为600 m的长方形地面,现要对该地面进行绿化,规划四周种花卉(花卉带的宽度相同),中间种草坪,若要求草坪的面积不小于总面积的一半,求花卉带宽度的范围.
易错警示 不等式变形前后不同解
| 素 养 达 成 |
1.解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集(体现了直观想象的核心素养).
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m
有口诀如下:大于取两边,小于取中间.
2.含参数的一元二次型的不等式
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”(体现了数学运算和逻辑推理的核心素养),讨论需从如下三个方面进行考虑:
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1<x2.
3.由一元二次不等式的解集可以逆推二次函数的零点及图象的开口方向.
【答案】B
【解析】因为2x+3-x2>0,所以x2-2x-3<0,方程x2-2x-3=0的根为-1,3,所以不等式的解集为{x|-1<x<3}.故选B.
2.(题型4)用一根长为100 m的绳子围成一个面积大于600 m2的矩形,设围成的矩形一边的长为x m,则x的取值范围为 ( )
A.{x|15<x<25} B.{x|20<x<30}
C.{x|25<x<35} D.{x|30<x<40}
【答案】B
【解析】设围成的矩形一边的长为x m,则另一边的长为(50-x) m,且0<x<50.由题意,得围成矩形的面积S=x(50-x)>600,即x2-50x+600<0,解得20<x<30.
4.(题型3)(2020年枣庄高一期中)已知关于x的不等式x2-5ax+b>0的解集为{x|x<1或x>4},则a+b=________.
【答案】5
【解析】根据不等式x2-5ax+b>0的解集为{x|x<1或x>4},知方程x2-5ax+b=0的两个根是1和4,则5a=1+4,b=1×4,解得a=1,b=4.所以a+b=5.
5.(题型1)解下列不等式:
(1)x(7-x)≥12;
(2)x2>2(x-1).
解:(1)原不等式可化为x2-7x+12≤0,
因为方程x2-7x+12=0的两根为x1=3,x2=4,
所以原不等式的解集为{x|3≤x≤4}.
(2)原不等式可以化为x2-2x+2>0,
因为判别式Δ=4-8=-4<0,
所以方程x2-2x+2=0无实根,而抛物线y=x2-2x+2开口向上,
所以原不等式的解集为R.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
