人教A版(2019)必修 第一册2.1 等式性质与不等式性质课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)必修 第一册2.1 等式性质与不等式性质课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 627.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
学习目标 素养要求
梳理等式的性质,理解不等式的概念,掌握不等式的性质,理解等式与不等式的共性与差异 数学建模
逻辑推理
| 自 学 导 引 |
1.不等式的概念:用数学符号“≠”“>”“<”“≥”或“≤”连接______或_____________,以表示它们之间的不等关系,含有这些______的式子叫做不等式.
两个数
用不等式表示不等关系
两个代数式
不等号
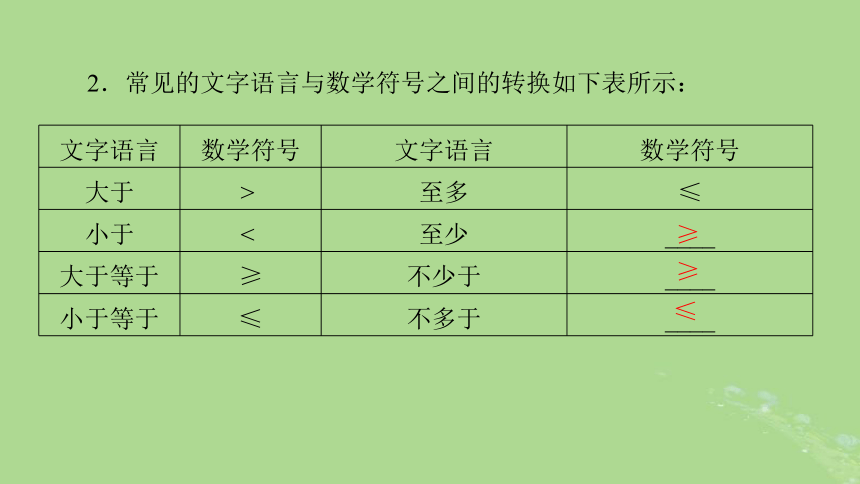
2.常见的文字语言与数学符号之间的转换如下表所示:
文字语言 数学符号 文字语言 数学符号
大于 > 至多 ≤
小于 < 至少 ____
大于等于 ≥ 不少于 ____
小于等于 ≤ 不多于 ____
≥
≥
≤
【预习自测】
某工厂在招标会上,购得甲材料x吨,乙材料y吨,若维持工厂正常生产,甲、乙两种材料总量至少需要120吨,则x,y应满足的不等关系是________.
【答案】x+y≥120
关于实数a,b大小的比较,有以下基本事实:
a-b>0 ________;a-b=0 a=b;a-b<0 ________.
a>b
实数大小比较的依据
a【预习自测】
已知a+b>0,b<0,那么a,b,-a,-b的大小关系是________.
【答案】a>-b>b>-a
等式的性质与不等式的性质的比较
等式的性质 不等式的性质
a=b b=a a>b ba=b,b=c a=c a>b,b>c a>c
a=b a+c=b+c a>b a+c>b+c
a=b ac=bc a>b,c>0 ac>bc;
a>b,c<0 aca=b,c=d a+c=b+d a>b,c>d ____________
a=b,c=d ac=bd a>b>0,c>d>0 ________
a=b≥0 an=bn a>b>0 an>bn(n∈N,n≥2)
a+c>b+d
ac>bd
【预习自测】判断下列命题是否正确.(正确的画“√”,错误的画“×”)
(1)不等式x≥2的含义是指x不小于2. ( )
(2)若a(3)若a>b,则ac>bc一定成立. ( )
(4)若a+c>b+d,则a>b,c>d. ( )
【答案】(1)√ (2)√ (3)× (4)×
【解析】(1)不等式x≥2表示x>2或x=2,即x不小于2.
(2)不等式a≤b表示a(3)由不等式的可乘性知,当不等式两端同乘一个正数时,不等号方向不变,因此若a>b,则ac>bc不一定成立.
(4)取a=4,c=5,b=6,d=2.满足a+c>b+d,但不满足a>b.
| 课 堂 互 动 |
(1)某车工计划在15天里加工零件408个,最初三天中,每天加工24个,则以后平均每天至少需加工多少个,才能在规定的时间内超额完成任务?请用不等式表示问题中的不等关系.
(2)用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,要求菜园的面积不小于110 m2,靠墙的一边长为x m.试用不等式表示其中的不等关系.
素养点睛:考查数学建模的核心素养.
题型1 用不等式(组)表示不等关系
将不等关系表示成不等式的思路
(1)读懂题意,找准不等关系所联系的量.
(2)用适当的不等号连接.
(3)多个不等关系用不等式组表示.
用不等式(组)表示不等关系时应注意的问题
在用不等式(组)表示不等关系时,应注意必须是具有相同性质,可以进行比较时,才可用,没有可比性的两个(或几个)量之间不能用不等式(组)来表示.
1.雷电的温度大约是28 000 ℃,比太阳表面温度的4.5倍还要高.设太阳表面温度为t ℃,那么t应满足的关系式是________.
【答案】4.5t<28 000
【解析】由题意得,太阳表面温度的4.5倍小于雷电的温度,即4.5t<28 000.
素养点睛:考查逻辑推理的核心素养.
题型2 代数式的大小比较
利用作差法比较大小的四个步骤
(1)作差:对要比较大小的两个式子作差.
(2)变形:对差式通过通分、因式分解、配方等手段进行变形.
(3)判断符号:对变形后的结果结合题设条件判断出差的符号.
(4)作出结论.
素养点睛:考查逻辑推理的核心素养.
题型3 不等式的性质的应用
利用不等式的性质求取值范围的注意点
(1)利用几个不等式的范围来确定某个不等式的范围要注意:同向不等式的两边可以相加(相乘),这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围.
(2)同向不等式具有可加性与可乘性,但是不能相减或相除,应用时,要充分利用所给条件进行适当变形来求范围,注意变形的等价性.
若a>b,则ac2________bc2.
错解:因为c2>0,且a>b,所以ac2>bc2,故填>.
易错防范:上面的解法错在忽视了c=0的情况.当c=0时,ac2=bc2.防范措施是使用不等式的性质时,不可忽视条件.
正解:因为c2≥0,且a>b,所以ac2≥bc2,故应填≥.
易错警示 忽视因式可能为0
巧题妙解 利用不等式的性质证明不等式
【思路点拨】不等式证明,就是利用不等式性质或者已知条件,推出不等式成立.
【精彩点拨】应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则.
| 素 养 达 成 |
1.比较两个实数的大小,只要求出它们的差并判断符号就可以了.
a-b>0 a>b;a-b=0 a=b;a-b<0 a<b.
2.作差法比较大小的一般步骤:
第一步:作差;
第二步:变形,常采用配方、因式分解等恒等变形手段,将“差”化成“和”或“积”;
第三步:定号,就是确定是大于0,等于0,还是小于0(不确定的要分情况讨论);
最后得结论.
概括为“三步一结论”,这里的“定号”是目的,“变形”是关键.
3.不等式的性质是不等式变形的依据,每一步变形都要严格依照性质进行,并注意不等式推导所需条件是否具备.不等式的性质的应用(体现了逻辑推理的核心素养).
1.(题型2)(2020年沈阳高一期中)设P=2a(a-2)+3,Q=(a-1)(a-3),a∈R,则有 ( )
A.P≥Q B.P>Q
C.P<Q D.P≤Q
【答案】A
【解析】P-Q=2a(a-2)+3-(a-1)(a-3)=a2≥0,所以P≥Q.故选A.
【答案】D
【解析】因为a,b,c∈R且a>b,所以取c=0,可排除A,B;取a=1,b=-1,可排除C.由不等式的性质知当a>b时,-2a<-2b,故D正确.故选D.
3.(题型1)完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20 000元,设请木工x人,瓦工y人,则其中的不等关系是 ( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
【答案】D
【解析】据题意知500x+400y≤20 000,即5x+4y≤200.故选D.
4.(题型2)(2020年天津月考)若x≠2且y≠-1,M=x2+y2-4x+2y,N=-5,则M与N的大小关系为________.
【答案】M>N
【解析】M-N=x2+y2-4x+2y+5=(x-2)2+(y+1)2,又x≠2,y≠-1,所以M>N.
5.(题型3)已知-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围.
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
学习目标 素养要求
梳理等式的性质,理解不等式的概念,掌握不等式的性质,理解等式与不等式的共性与差异 数学建模
逻辑推理
| 自 学 导 引 |
1.不等式的概念:用数学符号“≠”“>”“<”“≥”或“≤”连接______或_____________,以表示它们之间的不等关系,含有这些______的式子叫做不等式.
两个数
用不等式表示不等关系
两个代数式
不等号
2.常见的文字语言与数学符号之间的转换如下表所示:
文字语言 数学符号 文字语言 数学符号
大于 > 至多 ≤
小于 < 至少 ____
大于等于 ≥ 不少于 ____
小于等于 ≤ 不多于 ____
≥
≥
≤
【预习自测】
某工厂在招标会上,购得甲材料x吨,乙材料y吨,若维持工厂正常生产,甲、乙两种材料总量至少需要120吨,则x,y应满足的不等关系是________.
【答案】x+y≥120
关于实数a,b大小的比较,有以下基本事实:
a-b>0 ________;a-b=0 a=b;a-b<0 ________.
a>b
实数大小比较的依据
a
已知a+b>0,b<0,那么a,b,-a,-b的大小关系是________.
【答案】a>-b>b>-a
等式的性质与不等式的性质的比较
等式的性质 不等式的性质
a=b b=a a>b b
a=b a+c=b+c a>b a+c>b+c
a=b ac=bc a>b,c>0 ac>bc;
a>b,c<0 ac
a=b,c=d ac=bd a>b>0,c>d>0 ________
a=b≥0 an=bn a>b>0 an>bn(n∈N,n≥2)
a+c>b+d
ac>bd
【预习自测】判断下列命题是否正确.(正确的画“√”,错误的画“×”)
(1)不等式x≥2的含义是指x不小于2. ( )
(2)若a
(4)若a+c>b+d,则a>b,c>d. ( )
【答案】(1)√ (2)√ (3)× (4)×
【解析】(1)不等式x≥2表示x>2或x=2,即x不小于2.
(2)不等式a≤b表示a
(4)取a=4,c=5,b=6,d=2.满足a+c>b+d,但不满足a>b.
| 课 堂 互 动 |
(1)某车工计划在15天里加工零件408个,最初三天中,每天加工24个,则以后平均每天至少需加工多少个,才能在规定的时间内超额完成任务?请用不等式表示问题中的不等关系.
(2)用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,要求菜园的面积不小于110 m2,靠墙的一边长为x m.试用不等式表示其中的不等关系.
素养点睛:考查数学建模的核心素养.
题型1 用不等式(组)表示不等关系
将不等关系表示成不等式的思路
(1)读懂题意,找准不等关系所联系的量.
(2)用适当的不等号连接.
(3)多个不等关系用不等式组表示.
用不等式(组)表示不等关系时应注意的问题
在用不等式(组)表示不等关系时,应注意必须是具有相同性质,可以进行比较时,才可用,没有可比性的两个(或几个)量之间不能用不等式(组)来表示.
1.雷电的温度大约是28 000 ℃,比太阳表面温度的4.5倍还要高.设太阳表面温度为t ℃,那么t应满足的关系式是________.
【答案】4.5t<28 000
【解析】由题意得,太阳表面温度的4.5倍小于雷电的温度,即4.5t<28 000.
素养点睛:考查逻辑推理的核心素养.
题型2 代数式的大小比较
利用作差法比较大小的四个步骤
(1)作差:对要比较大小的两个式子作差.
(2)变形:对差式通过通分、因式分解、配方等手段进行变形.
(3)判断符号:对变形后的结果结合题设条件判断出差的符号.
(4)作出结论.
素养点睛:考查逻辑推理的核心素养.
题型3 不等式的性质的应用
利用不等式的性质求取值范围的注意点
(1)利用几个不等式的范围来确定某个不等式的范围要注意:同向不等式的两边可以相加(相乘),这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围.
(2)同向不等式具有可加性与可乘性,但是不能相减或相除,应用时,要充分利用所给条件进行适当变形来求范围,注意变形的等价性.
若a>b,则ac2________bc2.
错解:因为c2>0,且a>b,所以ac2>bc2,故填>.
易错防范:上面的解法错在忽视了c=0的情况.当c=0时,ac2=bc2.防范措施是使用不等式的性质时,不可忽视条件.
正解:因为c2≥0,且a>b,所以ac2≥bc2,故应填≥.
易错警示 忽视因式可能为0
巧题妙解 利用不等式的性质证明不等式
【思路点拨】不等式证明,就是利用不等式性质或者已知条件,推出不等式成立.
【精彩点拨】应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则.
| 素 养 达 成 |
1.比较两个实数的大小,只要求出它们的差并判断符号就可以了.
a-b>0 a>b;a-b=0 a=b;a-b<0 a<b.
2.作差法比较大小的一般步骤:
第一步:作差;
第二步:变形,常采用配方、因式分解等恒等变形手段,将“差”化成“和”或“积”;
第三步:定号,就是确定是大于0,等于0,还是小于0(不确定的要分情况讨论);
最后得结论.
概括为“三步一结论”,这里的“定号”是目的,“变形”是关键.
3.不等式的性质是不等式变形的依据,每一步变形都要严格依照性质进行,并注意不等式推导所需条件是否具备.不等式的性质的应用(体现了逻辑推理的核心素养).
1.(题型2)(2020年沈阳高一期中)设P=2a(a-2)+3,Q=(a-1)(a-3),a∈R,则有 ( )
A.P≥Q B.P>Q
C.P<Q D.P≤Q
【答案】A
【解析】P-Q=2a(a-2)+3-(a-1)(a-3)=a2≥0,所以P≥Q.故选A.
【答案】D
【解析】因为a,b,c∈R且a>b,所以取c=0,可排除A,B;取a=1,b=-1,可排除C.由不等式的性质知当a>b时,-2a<-2b,故D正确.故选D.
3.(题型1)完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算20 000元,设请木工x人,瓦工y人,则其中的不等关系是 ( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
【答案】D
【解析】据题意知500x+400y≤20 000,即5x+4y≤200.故选D.
4.(题型2)(2020年天津月考)若x≠2且y≠-1,M=x2+y2-4x+2y,N=-5,则M与N的大小关系为________.
【答案】M>N
【解析】M-N=x2+y2-4x+2y+5=(x-2)2+(y+1)2,又x≠2,y≠-1,所以M>N.
5.(题型3)已知-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
