高中数学人教A版(2019)必修第一册分层课时作业——2.2基本不等式(一般)(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册分层课时作业——2.2基本不等式(一般)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 607.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:16:32 | ||
图片预览




文档简介
一、单选题
1.若,则下面结论正确的有( )
A. B.若,则
C.若,则 D.若,则有最大值
2.已知函数对任意,都有,当,时,,则函数在,上的值域为( )
A., B., C., D.,
3.已知,,若,则的最小值是( )
A.2 B. C. D.
4.已知,条件,条件,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.若对任意正数,不等式恒成立,则实数的取值范围为
A., B. C. D.
6.已知,,且,则的最小值为( )
A.8 B. C.9 D.
二、多选题
7.若x,y满足,则( )
A. B.
C. D.
8.(多选)已知、均为正实数,则下列不等式不一定成立的是( )
A. B.
C. D.
三、填空题
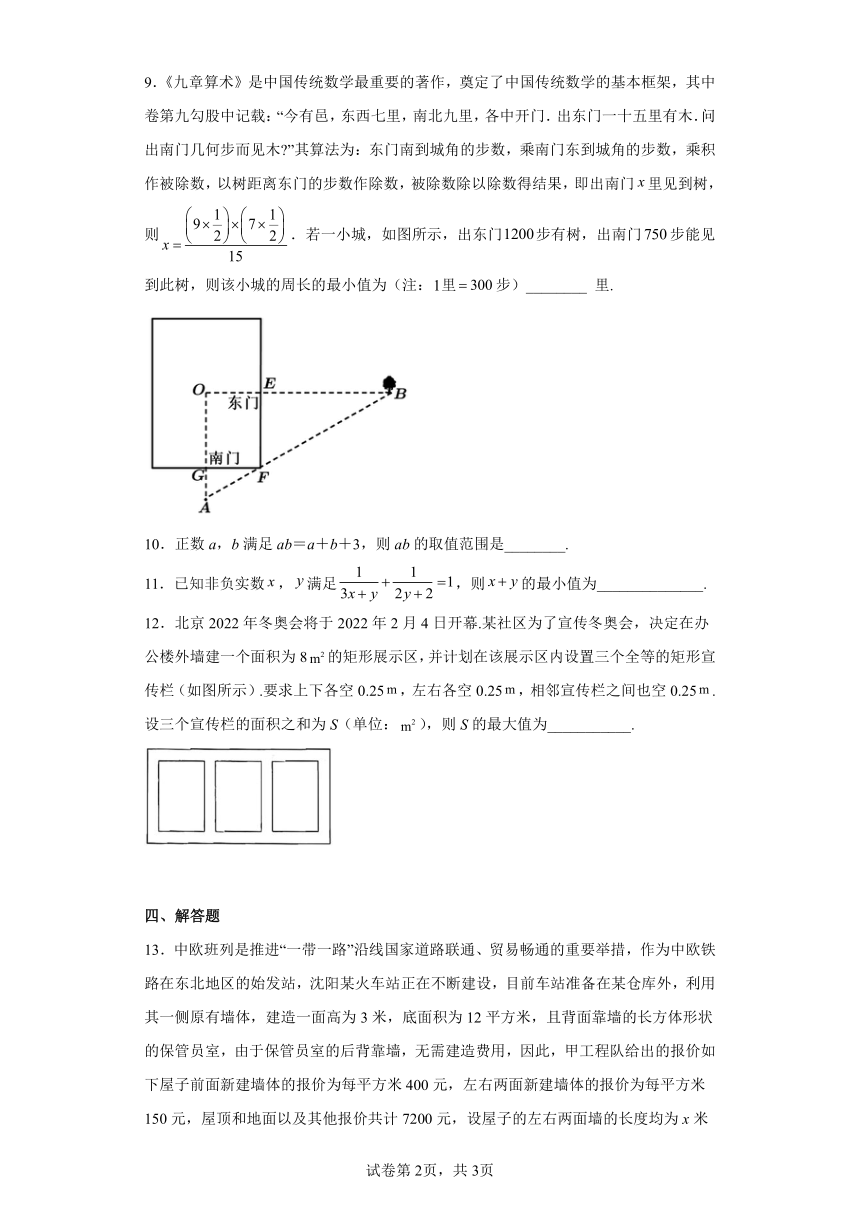
9.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木 ”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门里见到树,则.若一小城,如图所示,出东门步有树,出南门步能见到此树,则该小城的周长的最小值为(注:里步)________ 里.
10.正数a,b满足ab=a+b+3,则ab的取值范围是________.
11.已知非负实数,满足,则的最小值为______________.
12.北京2022年冬奥会将于2022年2月4日开幕.某社区为了宣传冬奥会,决定在办公楼外墙建一个面积为8的矩形展示区,并计划在该展示区内设置三个全等的矩形宣传栏(如图所示).要求上下各空0.25,左右各空0.25,相邻宣传栏之间也空0.25.设三个宣传栏的面积之和为S(单位:),则S的最大值为___________.
四、解答题
13.中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为3米,底面积为12平方米,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体的报价为每平方米150元,屋顶和地面以及其他报价共计7200元,设屋子的左右两面墙的长度均为x米.
(1)当左右两面墙的长度为多少米时,甲工程队的报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(a>0);若无论左右两面墙的长度为多少米,乙工程队都能竞标成功(报价低的工程队中标),求a的取值范围.
14.为持续推进“改善农村人居环境,建设宜居美丽乡村”,某村委计划在该村广场旁一矩形空地进行绿化.如图所示,两块完全相同的长方形种植绿草坪,草坪周围(斜线部分)均摆满宽度相同的花,已知两块绿草坪的面积均为400平方米.
(1)若矩形草坪的长比宽至少多9米,求草坪宽的最大值;
(2)若草坪四周及中间的花坛宽度均为2米,求整个绿化面积的最小值.
15.已知关于一元二次不等式的解集为.
(1)求函数的最小值;
(2)求关于的一元二次不等式的解集.
16.(1)证明:;
(2)若,,求的最大值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】对于选项ABD利用基本不等式化简整理求解即可判断,对于选项C取特值即可判断即可.
【详解】对于选项A:若,
由基本不等式得,即,
当且仅当时取等号;所以选项A不正确;
对于选项B:若,
,
,
当且仅当且,
即时取等号,所以选项B正确;
对于选项C:由,
,
即,
如时,,所以选项C不正确;
对于选项D:,当且仅当时取等
则有最大值,所以选项D不正确;
故选:B
2.D
【分析】当,时,,利用,将区间的自变量利用加减转化到区间上,从而进行值域的求解
【详解】当,时,,,
则当,时,即,,所以;
当,时,即,,
由,得,从而,;
当,时,即,,则,.
综上得函数在,上的值域为,.
故选:D.
3.C
【分析】将,转化为,由,利用基本不等式求解.
【详解】因为,
所以,
所以,
,
当且仅当,即时,等号成立,
故选:C
4.A
【分析】利用“1”的妙用探讨命题“若p则q”的真假,取特殊值计算说明“若q则p”的真假即可判断作答.
【详解】因为,由得:,
则,
当且仅当,即时取等号,因此,,
因,,由,取,则,,即,,
所以是的充分不必要条件.
故选:A
5.B
【分析】原不等式即,再利用基本不等式求得的最大值,可得的范围.
【详解】解:依题意得,当时, 恒成立,
又因为,当且仅当时取等号,
所以,的最大值为,所以,解得的取值范围为.
故选:.
【点睛】本题主要考查函数的恒成立问题,基本不等式的应用,属于中档题.
6.C
【分析】由题得,再利用基本不等式“1”的代换求最值.
【详解】因为,,,所以,
∴,
当且仅当取得等号,则的最小值为9.
故选:C
7.BC
【分析】根据基本不等式或者取特值即可判断各选项的真假.
【详解】因为(R),由可变形为,,解得,当且仅当时,,当且仅当时,,所以A错误,B正确;
由可变形为,解得,当且仅当时取等号,所以C正确;
因为变形可得,设,所以,因此
,所以当时满足等式,但是不成立,所以D错误.
故选:BC.
8.AD
【分析】A选项,利用基本不等式和可得出该不等式的正误;B选项,将不等式左边展开,然后利用基本不等式可验证该选项中的不等式是否成立;C选项,利用基本不等式以及可验证该选项中的不等式是否成立;D选项,取特殊值验证该选项中的不等式是否成立.
【详解】对于A,,当且仅当时等号同时成立;对于B,,当且仅当时取等号;
对于C,,当且仅当时取等号;
对于D,当,时,,,,
所以.
故选AD.
【点睛】本题考查利用基本不等式验证不等式是否成立,再利用基本不等式时要注意条件“一正、二定、三相等”的成立,考查推理能力,属于中等题.
9.
【分析】根据题意得出,进而可得出,结合基本不等式求的最小值即可.
【详解】因为里步,由图可知,步里,步里,
,则,且,
所以,,所以,,则,
所以,该小城的周长为(里).
故答案为:.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
10.
【分析】由题得ab=a+b+3≥2+3,解不等式即得解.
【详解】∵a,b是正数,
∴ab=a+b+3≥2+3(当且仅当a=b=3时等号成立),
所以,
所以,
所以或,
所以ab≥9.
故答案为:
【点睛】本题主要考查基本不等式的应用,意在考查学生对这些知识的理解掌握水平.
11.
【分析】将变形为,再借助“1”的妙用求解作答.
【详解】非负实数,满足,有,
则
,当且仅当,即时取“=”,
由,得,
所以当时,的最小值为.
故答案为:
12.
【分析】根据题意设矩形展示区的长为,则宽为,进而结合题意得,再根据基本不等式求解即可.
【详解】解:设矩形展示区的长为,则宽为,
因为该展示区内设置三个全等的矩形宣传栏,要求上下各空0.25,左右各空0.25,相邻宣传栏之间也空0.25,
所以,
当且仅当,即时等号成立,
所以S的最大值为
故答案为:
13.(1)当左右两面墙的长度为4米时,甲工程队的报价最低
(2)
【分析】(1)设总造价为元,列出.利用基本不等式求解函数的最值即可.
(2)由题意可得,对任意的,恒成立,参变分离可得恒成立,即,利用基本不等式求解函数的最值即可.
(1)
解:设甲工程队的总造价为y元,依题意左右两面墙的长度均为米,则屋子前面新建墙体长为米,
则
因为.
当且仅当,即时等号成立.
所以当时,,
即当左右两面墙的长度为4米时,甲工程队的报价最低为14400元.
(2)
解:由题意可得,对任意的恒成立,
即,从而,即恒成立,
又.
当且仅当,即时等号成立.
所以.
14.(1)最大值为16米;(2)最小值为平方米.
【分析】(1)设草坪的宽为x米,长为y米,依题意列出不等关系,求解即可;
(2)表示,利用均值不等式,即得最小值.
【详解】(1)设草坪的宽为x米,长为y米,由面积均为400平方米,得.
因为矩形草坪的长比宽至少大9米,所以,所以,解得.
又,所以.
所以宽的最大值为16米.
(2)记整个的绿化面积为S平方米,由题意可得
(平方米)
当且仅当米时,等号成立.
所以整个绿化面积的最小值为平方米.
15.(1)
(2)
【分析】(1)由题意可得,解不等式求出的取值范围,再利用基本不等式求的最小值;
(2)不等式化为,比较和的大小,即可得出不等式的解集.
(1)
因为关于一元二次不等式的解集为,
所以,化简可得:,解得:,
所以,
所以,
当且仅当即,的最小值为.
(2)
不等式,可化为,
因为,所以,
所以该不等式的解集为.
16.(1)证明见解析;(2).
【分析】(1)由不等式,令,则有,即可证得.
(2)由(1)得,化简得到,再由,即可求解.
【详解】(1)因为,与且仅当时,等号成立,
令,则有,当且仅当时,等号成立,即.
(2)由(1)得,即,当且仅当时,等号成立,
所以,
又因为,
当且仅当时,等号成立,即,即,等号成立,
所以,即,
所以当,时,取到最大值,且最大值为.
【点睛】利用基本不等式求解实际问题的解题技巧:
1、利用基本不等式求解实际应用问题时,一定要注意变量的实际意义及其取值范围;
2、根据实际问题抽象出函数的解析式,再利用基本不等式求得函数的最值;
3、在应用基本不等式求最值时,若等号取不到,可利用函数的单调性求解.
答案第1页,共2页
答案第1页,共2页
1.若,则下面结论正确的有( )
A. B.若,则
C.若,则 D.若,则有最大值
2.已知函数对任意,都有,当,时,,则函数在,上的值域为( )
A., B., C., D.,
3.已知,,若,则的最小值是( )
A.2 B. C. D.
4.已知,条件,条件,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.若对任意正数,不等式恒成立,则实数的取值范围为
A., B. C. D.
6.已知,,且,则的最小值为( )
A.8 B. C.9 D.
二、多选题
7.若x,y满足,则( )
A. B.
C. D.
8.(多选)已知、均为正实数,则下列不等式不一定成立的是( )
A. B.
C. D.
三、填空题
9.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木 ”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门里见到树,则.若一小城,如图所示,出东门步有树,出南门步能见到此树,则该小城的周长的最小值为(注:里步)________ 里.
10.正数a,b满足ab=a+b+3,则ab的取值范围是________.
11.已知非负实数,满足,则的最小值为______________.
12.北京2022年冬奥会将于2022年2月4日开幕.某社区为了宣传冬奥会,决定在办公楼外墙建一个面积为8的矩形展示区,并计划在该展示区内设置三个全等的矩形宣传栏(如图所示).要求上下各空0.25,左右各空0.25,相邻宣传栏之间也空0.25.设三个宣传栏的面积之和为S(单位:),则S的最大值为___________.
四、解答题
13.中欧班列是推进“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设,目前车站准备在某仓库外,利用其一侧原有墙体,建造一面高为3米,底面积为12平方米,且背面靠墙的长方体形状的保管员室,由于保管员室的后背靠墙,无需建造费用,因此,甲工程队给出的报价如下屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体的报价为每平方米150元,屋顶和地面以及其他报价共计7200元,设屋子的左右两面墙的长度均为x米.
(1)当左右两面墙的长度为多少米时,甲工程队的报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(a>0);若无论左右两面墙的长度为多少米,乙工程队都能竞标成功(报价低的工程队中标),求a的取值范围.
14.为持续推进“改善农村人居环境,建设宜居美丽乡村”,某村委计划在该村广场旁一矩形空地进行绿化.如图所示,两块完全相同的长方形种植绿草坪,草坪周围(斜线部分)均摆满宽度相同的花,已知两块绿草坪的面积均为400平方米.
(1)若矩形草坪的长比宽至少多9米,求草坪宽的最大值;
(2)若草坪四周及中间的花坛宽度均为2米,求整个绿化面积的最小值.
15.已知关于一元二次不等式的解集为.
(1)求函数的最小值;
(2)求关于的一元二次不等式的解集.
16.(1)证明:;
(2)若,,求的最大值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】对于选项ABD利用基本不等式化简整理求解即可判断,对于选项C取特值即可判断即可.
【详解】对于选项A:若,
由基本不等式得,即,
当且仅当时取等号;所以选项A不正确;
对于选项B:若,
,
,
当且仅当且,
即时取等号,所以选项B正确;
对于选项C:由,
,
即,
如时,,所以选项C不正确;
对于选项D:,当且仅当时取等
则有最大值,所以选项D不正确;
故选:B
2.D
【分析】当,时,,利用,将区间的自变量利用加减转化到区间上,从而进行值域的求解
【详解】当,时,,,
则当,时,即,,所以;
当,时,即,,
由,得,从而,;
当,时,即,,则,.
综上得函数在,上的值域为,.
故选:D.
3.C
【分析】将,转化为,由,利用基本不等式求解.
【详解】因为,
所以,
所以,
,
当且仅当,即时,等号成立,
故选:C
4.A
【分析】利用“1”的妙用探讨命题“若p则q”的真假,取特殊值计算说明“若q则p”的真假即可判断作答.
【详解】因为,由得:,
则,
当且仅当,即时取等号,因此,,
因,,由,取,则,,即,,
所以是的充分不必要条件.
故选:A
5.B
【分析】原不等式即,再利用基本不等式求得的最大值,可得的范围.
【详解】解:依题意得,当时, 恒成立,
又因为,当且仅当时取等号,
所以,的最大值为,所以,解得的取值范围为.
故选:.
【点睛】本题主要考查函数的恒成立问题,基本不等式的应用,属于中档题.
6.C
【分析】由题得,再利用基本不等式“1”的代换求最值.
【详解】因为,,,所以,
∴,
当且仅当取得等号,则的最小值为9.
故选:C
7.BC
【分析】根据基本不等式或者取特值即可判断各选项的真假.
【详解】因为(R),由可变形为,,解得,当且仅当时,,当且仅当时,,所以A错误,B正确;
由可变形为,解得,当且仅当时取等号,所以C正确;
因为变形可得,设,所以,因此
,所以当时满足等式,但是不成立,所以D错误.
故选:BC.
8.AD
【分析】A选项,利用基本不等式和可得出该不等式的正误;B选项,将不等式左边展开,然后利用基本不等式可验证该选项中的不等式是否成立;C选项,利用基本不等式以及可验证该选项中的不等式是否成立;D选项,取特殊值验证该选项中的不等式是否成立.
【详解】对于A,,当且仅当时等号同时成立;对于B,,当且仅当时取等号;
对于C,,当且仅当时取等号;
对于D,当,时,,,,
所以.
故选AD.
【点睛】本题考查利用基本不等式验证不等式是否成立,再利用基本不等式时要注意条件“一正、二定、三相等”的成立,考查推理能力,属于中等题.
9.
【分析】根据题意得出,进而可得出,结合基本不等式求的最小值即可.
【详解】因为里步,由图可知,步里,步里,
,则,且,
所以,,所以,,则,
所以,该小城的周长为(里).
故答案为:.
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
10.
【分析】由题得ab=a+b+3≥2+3,解不等式即得解.
【详解】∵a,b是正数,
∴ab=a+b+3≥2+3(当且仅当a=b=3时等号成立),
所以,
所以,
所以或,
所以ab≥9.
故答案为:
【点睛】本题主要考查基本不等式的应用,意在考查学生对这些知识的理解掌握水平.
11.
【分析】将变形为,再借助“1”的妙用求解作答.
【详解】非负实数,满足,有,
则
,当且仅当,即时取“=”,
由,得,
所以当时,的最小值为.
故答案为:
12.
【分析】根据题意设矩形展示区的长为,则宽为,进而结合题意得,再根据基本不等式求解即可.
【详解】解:设矩形展示区的长为,则宽为,
因为该展示区内设置三个全等的矩形宣传栏,要求上下各空0.25,左右各空0.25,相邻宣传栏之间也空0.25,
所以,
当且仅当,即时等号成立,
所以S的最大值为
故答案为:
13.(1)当左右两面墙的长度为4米时,甲工程队的报价最低
(2)
【分析】(1)设总造价为元,列出.利用基本不等式求解函数的最值即可.
(2)由题意可得,对任意的,恒成立,参变分离可得恒成立,即,利用基本不等式求解函数的最值即可.
(1)
解:设甲工程队的总造价为y元,依题意左右两面墙的长度均为米,则屋子前面新建墙体长为米,
则
因为.
当且仅当,即时等号成立.
所以当时,,
即当左右两面墙的长度为4米时,甲工程队的报价最低为14400元.
(2)
解:由题意可得,对任意的恒成立,
即,从而,即恒成立,
又.
当且仅当,即时等号成立.
所以.
14.(1)最大值为16米;(2)最小值为平方米.
【分析】(1)设草坪的宽为x米,长为y米,依题意列出不等关系,求解即可;
(2)表示,利用均值不等式,即得最小值.
【详解】(1)设草坪的宽为x米,长为y米,由面积均为400平方米,得.
因为矩形草坪的长比宽至少大9米,所以,所以,解得.
又,所以.
所以宽的最大值为16米.
(2)记整个的绿化面积为S平方米,由题意可得
(平方米)
当且仅当米时,等号成立.
所以整个绿化面积的最小值为平方米.
15.(1)
(2)
【分析】(1)由题意可得,解不等式求出的取值范围,再利用基本不等式求的最小值;
(2)不等式化为,比较和的大小,即可得出不等式的解集.
(1)
因为关于一元二次不等式的解集为,
所以,化简可得:,解得:,
所以,
所以,
当且仅当即,的最小值为.
(2)
不等式,可化为,
因为,所以,
所以该不等式的解集为.
16.(1)证明见解析;(2).
【分析】(1)由不等式,令,则有,即可证得.
(2)由(1)得,化简得到,再由,即可求解.
【详解】(1)因为,与且仅当时,等号成立,
令,则有,当且仅当时,等号成立,即.
(2)由(1)得,即,当且仅当时,等号成立,
所以,
又因为,
当且仅当时,等号成立,即,即,等号成立,
所以,即,
所以当,时,取到最大值,且最大值为.
【点睛】利用基本不等式求解实际问题的解题技巧:
1、利用基本不等式求解实际应用问题时,一定要注意变量的实际意义及其取值范围;
2、根据实际问题抽象出函数的解析式,再利用基本不等式求得函数的最值;
3、在应用基本不等式求最值时,若等号取不到,可利用函数的单调性求解.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
