第8章 成对数据的统计分析 综合复习-【新教材】人教A版(2019)高中数学选择性必修第三册 课件(12张PPT)
文档属性
| 名称 | 第8章 成对数据的统计分析 综合复习-【新教材】人教A版(2019)高中数学选择性必修第三册 课件(12张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 466.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:01:05 | ||
图片预览





文档简介
(共12张PPT)
第八章
成对数据的统计分析综合复习
一:知识复习
1、两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
2、样本相关系数r
(1)当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
(2)r 的取值范围为[-1,1]
(3)当|r|越接近1时,成对样本数据的线性相关程度越强;
当|r|越接近0时,成对样本数据的线性相关程度越弱.
一:知识复习
我们称①式为Y关于x的一元线性回归模型.其中, Y称为因变量或响应变量, x称为自变量或解释变量.a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
①
3、一元线性回归模型
一:知识复习
4、经验回归方程
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法.
我们称yi为随机变量Y的观测值,通过经验回归方程得到的为预测值.为了研究回归模型的有效性,定义残差为=yi-,残差是随机误差的估计值,通过对残差的分析可判断回归模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面的工作称为残差分析.
5、残差
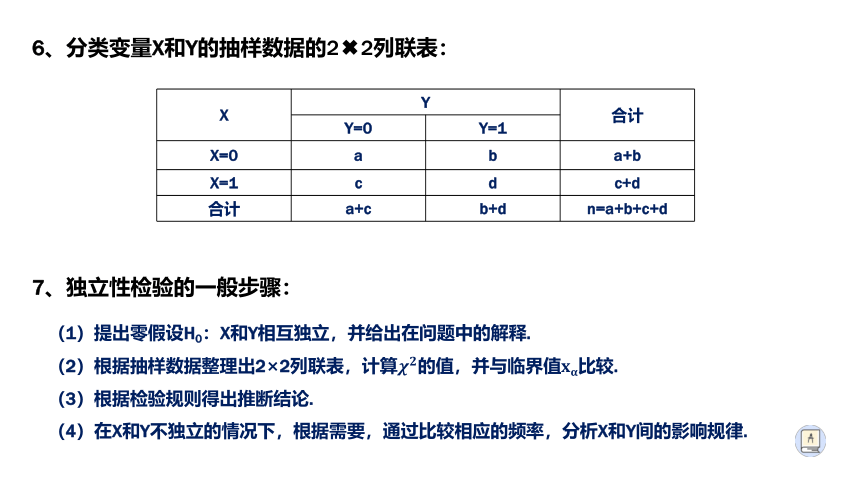
7、独立性检验的一般步骤:
6、分类变量X和Y的抽样数据的2 2列联表:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算的值,并与临界值比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
二:典型例题
二:典型例题
二:典型例题
二:典型例题
二:典型例题
第八章
成对数据的统计分析综合复习
一:知识复习
1、两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
2、样本相关系数r
(1)当r>0时,称成对样本数据正相关;
当r<0时,称成对样本数据负相关.
(2)r 的取值范围为[-1,1]
(3)当|r|越接近1时,成对样本数据的线性相关程度越强;
当|r|越接近0时,成对样本数据的线性相关程度越弱.
一:知识复习
我们称①式为Y关于x的一元线性回归模型.其中, Y称为因变量或响应变量, x称为自变量或解释变量.a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
①
3、一元线性回归模型
一:知识复习
4、经验回归方程
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法.
我们称yi为随机变量Y的观测值,通过经验回归方程得到的为预测值.为了研究回归模型的有效性,定义残差为=yi-,残差是随机误差的估计值,通过对残差的分析可判断回归模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面的工作称为残差分析.
5、残差
7、独立性检验的一般步骤:
6、分类变量X和Y的抽样数据的2 2列联表:
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算的值,并与临界值比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
二:典型例题
二:典型例题
二:典型例题
二:典型例题
二:典型例题
