第6章 计数原理 综合复习-【新教材】人教A版(2019)高中数学选择性必修第三册 课件(22张PPT)
文档属性
| 名称 | 第6章 计数原理 综合复习-【新教材】人教A版(2019)高中数学选择性必修第三册 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 496.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:01:05 | ||
图片预览







文档简介
(共22张PPT)
第六章 计数原理综合复习
一:知识复习
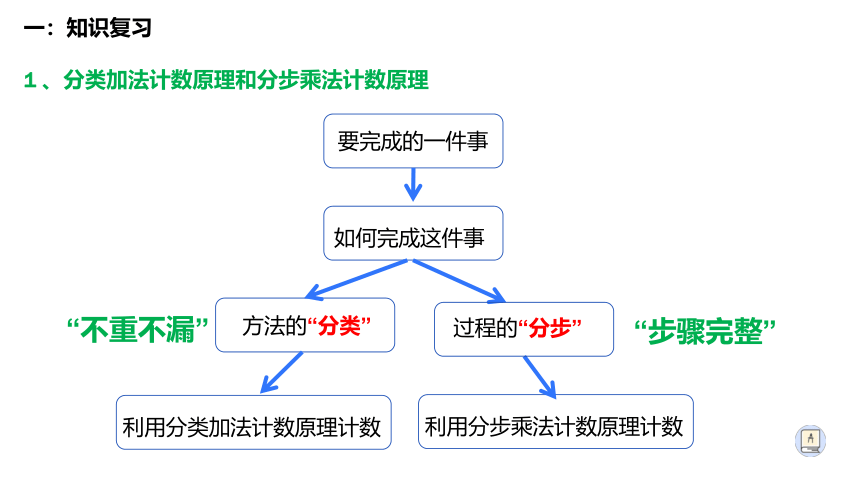
1 、分类加法计数原理和分步乘法计数原理
要完成的一件事
如何完成这件事
方法的“分类”
利用分类加法计数原理计数
利用分步乘法计数原理计数
过程的“分步”
“不重不漏”
“步骤完整”
一:知识复习
2、排列数、组合数的公式及性质
一:知识复习
3、二项式定理
(1)展开式共有 n+1 项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;
字母b按升幂排列,次数由0递增到n.
(4)二项展开式中,系数 叫作二项式系数,即
(3)二项展开式的通项:
一:知识复习
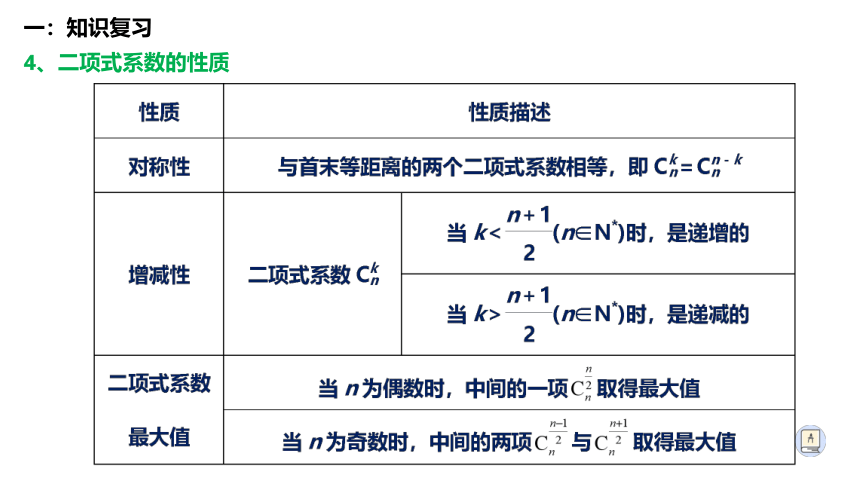
4、二项式系数的性质
一:知识复习
5、各二项式系数和
二:典型例题
题型一:排列问题
【例1】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
方法小结
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
定序问题除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反、等价转化的方法
求解排列问题的6种主要方法
二:典型例题
题型二:组合问题
【例2】某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
(2)其中某一种假货不能在内,不同取法有多少种?
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
方法小结
组合问题的2类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
二:典型例题
题型三:分组分配问题
【例3】六本不同的书,按下列要求各有多少种不同的分法?
(1) 分给甲、乙、丙三人,甲得一本,乙得两本,丙得三本;
(2) 分给甲、乙、丙三人,每人两本;
(3) 分给甲、乙、丙三人,甲得四本,乙得一本,丙得一本;
(4)分为三份,一份一本,一份两本,一份三本;
(5)分为三份,每份两本;
(6)分为三份,一份四本,一份一本,一份一本;
(7)分给甲、乙、丙三人,一人一本,一人两本,一人三本;
(8)分给甲、乙、丙三人,一人得四本,另外两个人每个人得一本;
(9)分给甲、乙、丙三人,每人至少一本.
答案:(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(1)完全平均分组:在分组时,每组元素的个数都相等.
①只分组无分配时,需要除以这几组的“全排列”,以确保消去重复;
②分组且分配时,一种方法是先分组再分配;另一种方法是可以用分步乘法
计数原理解题.
(2)部分平均分组:在分组时,每组的个数是不均等的,而是有一部分个数相同.
需要除以相同的组的“全排列”,保证没有重复.
(3)非平均分组:每组所要分的元素个数是不相同的.这种分组不考虑重复现象。
解题思想:先分组、后分配
方法小结
分组分配问题
二:典型例题
题型四:涂色问题
【例4】现用五种不同的颜色,要对如图中的四个部分进行着色,要求公共边的两块不能用同一种颜色,共有__________种不同着色方法 .
二:典型例题
题型五:多面手问题
【例5】某龙舟队有9名队员,其中3人只会划左舷,4人只会划右舷,2人既会划左舷又会划右舷.现要选派划左舷的3人、右舷的3人共6人去参加比赛,则不同的选派方法共有
A.56种 B. 68种 C. 74种 D. 92种
二:典型例题
题型六:求展开式中指定的项或某一项的系数或二项式系数
(1)求展开式中的特定项.可依据条件写出第r+1项,再由特定项的特点求出r值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第r+1项,由特定项得出r值,最后求出其参数.
方法小结
求二项展开式有关问题的方法
二:典型例题
题型七:二项式系数的性质与各项系数和
第六章 计数原理综合复习
一:知识复习
1 、分类加法计数原理和分步乘法计数原理
要完成的一件事
如何完成这件事
方法的“分类”
利用分类加法计数原理计数
利用分步乘法计数原理计数
过程的“分步”
“不重不漏”
“步骤完整”
一:知识复习
2、排列数、组合数的公式及性质
一:知识复习
3、二项式定理
(1)展开式共有 n+1 项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;
字母b按升幂排列,次数由0递增到n.
(4)二项展开式中,系数 叫作二项式系数,即
(3)二项展开式的通项:
一:知识复习
4、二项式系数的性质
一:知识复习
5、各二项式系数和
二:典型例题
题型一:排列问题
【例1】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
方法小结
直接法 把符合条件的排列数直接列式计算
优先法 优先安排特殊元素或特殊位置
捆绑法 把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
插空法 对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
定序问题除法处理 对于定序问题,可先不考虑顺序限制,排列后,再除以定序元素的全排列
间接法 正难则反、等价转化的方法
求解排列问题的6种主要方法
二:典型例题
题型二:组合问题
【例2】某市工商局对35种商品进行抽样检查,已知其中有15种假货.现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
(2)其中某一种假货不能在内,不同取法有多少种?
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
方法小结
组合问题的2类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外的元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
(2)“至少”或“至多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
二:典型例题
题型三:分组分配问题
【例3】六本不同的书,按下列要求各有多少种不同的分法?
(1) 分给甲、乙、丙三人,甲得一本,乙得两本,丙得三本;
(2) 分给甲、乙、丙三人,每人两本;
(3) 分给甲、乙、丙三人,甲得四本,乙得一本,丙得一本;
(4)分为三份,一份一本,一份两本,一份三本;
(5)分为三份,每份两本;
(6)分为三份,一份四本,一份一本,一份一本;
(7)分给甲、乙、丙三人,一人一本,一人两本,一人三本;
(8)分给甲、乙、丙三人,一人得四本,另外两个人每个人得一本;
(9)分给甲、乙、丙三人,每人至少一本.
答案:(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(1)完全平均分组:在分组时,每组元素的个数都相等.
①只分组无分配时,需要除以这几组的“全排列”,以确保消去重复;
②分组且分配时,一种方法是先分组再分配;另一种方法是可以用分步乘法
计数原理解题.
(2)部分平均分组:在分组时,每组的个数是不均等的,而是有一部分个数相同.
需要除以相同的组的“全排列”,保证没有重复.
(3)非平均分组:每组所要分的元素个数是不相同的.这种分组不考虑重复现象。
解题思想:先分组、后分配
方法小结
分组分配问题
二:典型例题
题型四:涂色问题
【例4】现用五种不同的颜色,要对如图中的四个部分进行着色,要求公共边的两块不能用同一种颜色,共有__________种不同着色方法 .
二:典型例题
题型五:多面手问题
【例5】某龙舟队有9名队员,其中3人只会划左舷,4人只会划右舷,2人既会划左舷又会划右舷.现要选派划左舷的3人、右舷的3人共6人去参加比赛,则不同的选派方法共有
A.56种 B. 68种 C. 74种 D. 92种
二:典型例题
题型六:求展开式中指定的项或某一项的系数或二项式系数
(1)求展开式中的特定项.可依据条件写出第r+1项,再由特定项的特点求出r值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第r+1项,由特定项得出r值,最后求出其参数.
方法小结
求二项展开式有关问题的方法
二:典型例题
题型七:二项式系数的性质与各项系数和
