数学北师大版(2019)必修第一册1.1.2集合的基本关系教案(2)
文档属性
| 名称 | 数学北师大版(2019)必修第一册1.1.2集合的基本关系教案(2) |  | |
| 格式 | docx | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:22:16 | ||
图片预览

文档简介
第一章 集合
第1.2节 集合的基本关系
课本从学生熟悉的集合(有理数的集合、实数的集合等)出发,通过类比实数间的大小关系引入集合间的关系,同时,结合相关内容介绍子集等概念.再安排这部分内容时,课本注重体现逻辑思考的方法,如类比等值;注意的问题:在集合间的关系教学中,建议重视使用Venn图,这有助于学生通过体会直观图示来理解抽象概念;随着学习的深入,集合符号越来越多,建议教学时引导学生区分一些容易混淆的关系和符号,例如∈与的区别.
一:教学目标
了解集合之间的包含、相等关系的含义;理解子集、真子集的概念;能利用Venn图表达集合间的关系;了解与空集的含义。
二:核心素养
数学抽象:子集,真子集的含义
逻辑推理:运用集合与集合关系推理实际问题
数学运算:求子集个数;由集合与集合的关系求参数值或范围,
直观想象:在理解子集和真子集含义以及空集与集合关系的过程中,提高学生分析问题和概念判断能力
数学建模:从实例理解子集含义的过程中,提高语言转换和抽象概括能力。
教学重点:集合的包含关系、子集、真子集、集合相等的概念以及符号表示。
教学难点:属于、包含关系的区别,包含与相等关系的区别,
PPT
实例分析
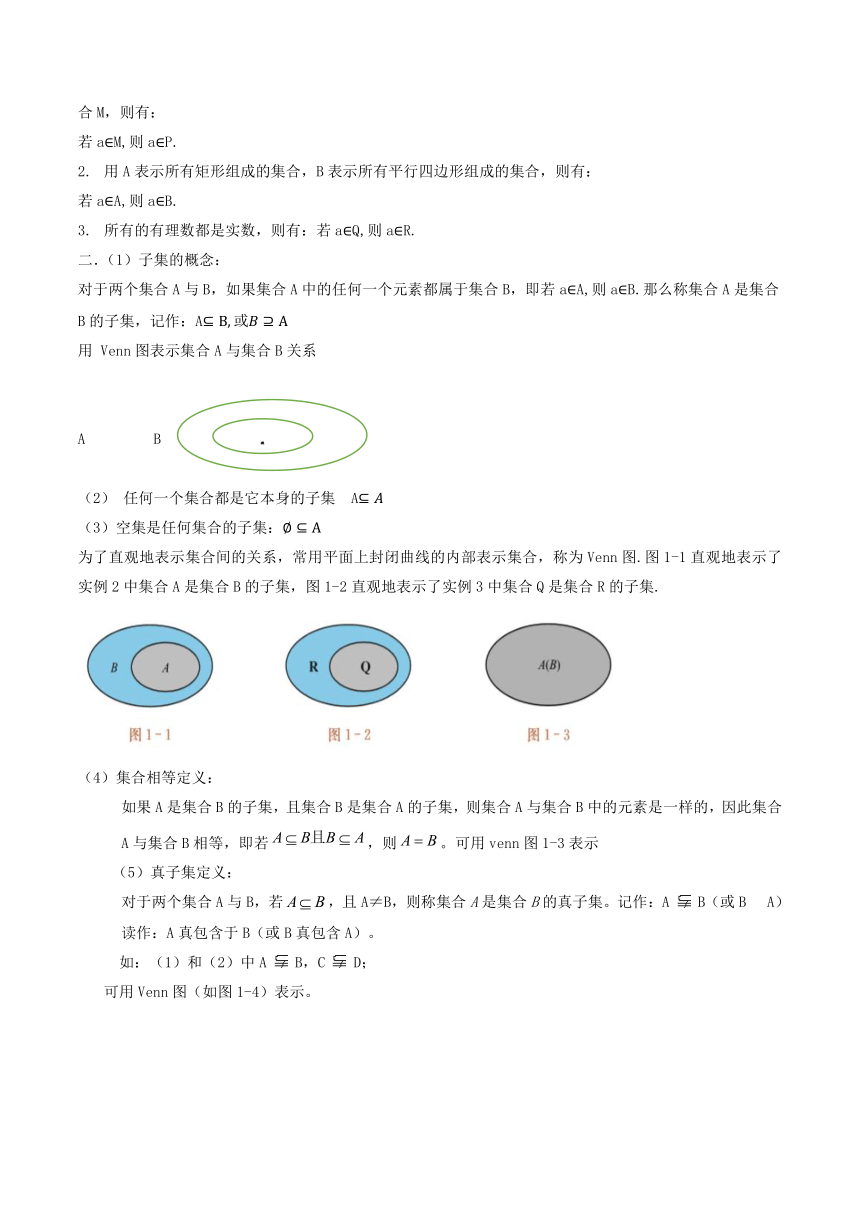
设某校高一(1)班全体35位同学组成集合P,其中女生组成集合M,则有:
若aM,则aP.
用A表示所有矩形组成的集合,B表示所有平行四边形组成的集合,则有:
若aA,则aB.
所有的有理数都是实数,则有:若aQ,则aR.
二.(1)子集的概念:
对于两个集合A与B,如果集合A中的任何一个元素都属于集合B,即若aA,则aB.那么称集合A是集合B的子集,记作:A
用 Venn图表示集合A与集合B关系
(
A
)
A B
(2) 任何一个集合都是它本身的子集 A
(3)空集是任何集合的子集:
为了直观地表示集合间的关系,常用平面上封闭曲线的内部表示集合,称为Venn图.图1-1直观地表示了实例2中集合A是集合B的子集,图1-2直观地表示了实例3中集合Q是集合R的子集.
(4)集合相等定义:
如果A是集合B的子集,且集合B是集合A的子集,则集合A与集合B中的元素是一样的,因此集合A与集合B相等,即若,则。可用venn图1-3表示
(5)真子集定义:
对于两个集合A与B,若,且A≠B,则称集合A是集合B的真子集。记作:A B(或B A) 读作:A真包含于B(或B真包含A)。
如:(1)和(2)中A B,C D;
可用Venn图(如图1-4)表示。
例题1:(1)判断集合与集合的关系
{x|(x-7)(x+5)=0}_______{-5, 7}
{a,b,c, }____B={a,b}
N+ ___N_____Z____Q____R
{x|x}____{x|x}
(2)用适当的符号填空:
_____ ; 0 _____ ; ______ ; ______
(3)关于子集,真子集个数
例题2: 写出集合{0,1,2}的所有子集并指出其中那些是真子集。
解析:子集:{0},{1},{2},{0,1}{0,2}{1,2}{0,1,2},
真子集:{0},{1},{2},{0,1}{0,2}{1,2}{0,1,2}
总结:子集:8个;真子集:7个
【课堂练习一】:写出集合以下集合的子集和真子集,并说明个数
1.{4}; 2.{3,4}; 3.{3,4,5,} 4,{3,4,5,6,}
课堂小结:若一个集合有n个元素,则它的子集有:2n 个 ;真子集:2n-1 个;
非空真子集:2n-2个
【课堂练习二】:判断下列叙述正确性:
1. ={0};
2. 任何一个集合必有两个或两个以上的子集;
3. 空集没有子集;
4. 空集是任何一个集合的子集.
5.空集是任何集合的真子集;
6.若 A,则A≠ .
课堂小结:正确理解空集与集合的关系
例题3:某造纸厂生产练习本用纸,在纸的密度和厚度都合格时,该产品才合格,若用A表示练习本用纸合格的产品组成的集合,B表示纸的密度合格的产品组成的集合,C表示纸的厚度合格的产品组成的集合,则下列包含关系那个成立?
A B, B A, CA
试用用venn图表示这三个集合的关系。
解析:由题意知:A B, A, 成立,它们的关系可用venn图表示
【知识扩充】利用集合与集合之间关系解决参数问题
例题4:
(1) 已知集合A={﹣1,2},B={x|ax=1},若B A,则由实数a的所有可能的取值组成的集合为( )
A. B. C. D.
【答案】:D
(2)若集合A=(a,,1)又可表示为{a2,a+b,0},求a2018+b2019的值.
【答案】:∵a≠0,∴=0,∴b=0,∴a=﹣1,
∴a2018+b2019=(﹣1)2018+02019=1.
(3)若A={x|﹣2≤x≤3},B={x|2m﹣1≤x≤m+1},
(1)当B A时,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
【答案】:(1)B A,若B= ,则2m﹣1>m+1,∴m>2;
若B≠ ,则,解得;
∴实数m的取值范围是;
(2)根据已知条件知:A∩B= ;
∴若B= ,由(1)知,m>2;
若B≠ ,则,解得m<﹣3;
∴实数m的取值范围为(﹣∞,﹣3)∪(2,+∞).
本节课从实例入手,非常自然贴切地引出子集、真子集、空集、相等的概念及符号;并用Venn图直观地把这种关系表示出来;注意包含与属于符号的运用。
第1.2节 集合的基本关系
课本从学生熟悉的集合(有理数的集合、实数的集合等)出发,通过类比实数间的大小关系引入集合间的关系,同时,结合相关内容介绍子集等概念.再安排这部分内容时,课本注重体现逻辑思考的方法,如类比等值;注意的问题:在集合间的关系教学中,建议重视使用Venn图,这有助于学生通过体会直观图示来理解抽象概念;随着学习的深入,集合符号越来越多,建议教学时引导学生区分一些容易混淆的关系和符号,例如∈与的区别.
一:教学目标
了解集合之间的包含、相等关系的含义;理解子集、真子集的概念;能利用Venn图表达集合间的关系;了解与空集的含义。
二:核心素养
数学抽象:子集,真子集的含义
逻辑推理:运用集合与集合关系推理实际问题
数学运算:求子集个数;由集合与集合的关系求参数值或范围,
直观想象:在理解子集和真子集含义以及空集与集合关系的过程中,提高学生分析问题和概念判断能力
数学建模:从实例理解子集含义的过程中,提高语言转换和抽象概括能力。
教学重点:集合的包含关系、子集、真子集、集合相等的概念以及符号表示。
教学难点:属于、包含关系的区别,包含与相等关系的区别,
PPT
实例分析
设某校高一(1)班全体35位同学组成集合P,其中女生组成集合M,则有:
若aM,则aP.
用A表示所有矩形组成的集合,B表示所有平行四边形组成的集合,则有:
若aA,则aB.
所有的有理数都是实数,则有:若aQ,则aR.
二.(1)子集的概念:
对于两个集合A与B,如果集合A中的任何一个元素都属于集合B,即若aA,则aB.那么称集合A是集合B的子集,记作:A
用 Venn图表示集合A与集合B关系
(
A
)
A B
(2) 任何一个集合都是它本身的子集 A
(3)空集是任何集合的子集:
为了直观地表示集合间的关系,常用平面上封闭曲线的内部表示集合,称为Venn图.图1-1直观地表示了实例2中集合A是集合B的子集,图1-2直观地表示了实例3中集合Q是集合R的子集.
(4)集合相等定义:
如果A是集合B的子集,且集合B是集合A的子集,则集合A与集合B中的元素是一样的,因此集合A与集合B相等,即若,则。可用venn图1-3表示
(5)真子集定义:
对于两个集合A与B,若,且A≠B,则称集合A是集合B的真子集。记作:A B(或B A) 读作:A真包含于B(或B真包含A)。
如:(1)和(2)中A B,C D;
可用Venn图(如图1-4)表示。
例题1:(1)判断集合与集合的关系
{x|(x-7)(x+5)=0}_______{-5, 7}
{a,b,c, }____B={a,b}
N+ ___N_____Z____Q____R
{x|x}____{x|x}
(2)用适当的符号填空:
_____ ; 0 _____ ; ______ ; ______
(3)关于子集,真子集个数
例题2: 写出集合{0,1,2}的所有子集并指出其中那些是真子集。
解析:子集:{0},{1},{2},{0,1}{0,2}{1,2}{0,1,2},
真子集:{0},{1},{2},{0,1}{0,2}{1,2}{0,1,2}
总结:子集:8个;真子集:7个
【课堂练习一】:写出集合以下集合的子集和真子集,并说明个数
1.{4}; 2.{3,4}; 3.{3,4,5,} 4,{3,4,5,6,}
课堂小结:若一个集合有n个元素,则它的子集有:2n 个 ;真子集:2n-1 个;
非空真子集:2n-2个
【课堂练习二】:判断下列叙述正确性:
1. ={0};
2. 任何一个集合必有两个或两个以上的子集;
3. 空集没有子集;
4. 空集是任何一个集合的子集.
5.空集是任何集合的真子集;
6.若 A,则A≠ .
课堂小结:正确理解空集与集合的关系
例题3:某造纸厂生产练习本用纸,在纸的密度和厚度都合格时,该产品才合格,若用A表示练习本用纸合格的产品组成的集合,B表示纸的密度合格的产品组成的集合,C表示纸的厚度合格的产品组成的集合,则下列包含关系那个成立?
A B, B A, CA
试用用venn图表示这三个集合的关系。
解析:由题意知:A B, A, 成立,它们的关系可用venn图表示
【知识扩充】利用集合与集合之间关系解决参数问题
例题4:
(1) 已知集合A={﹣1,2},B={x|ax=1},若B A,则由实数a的所有可能的取值组成的集合为( )
A. B. C. D.
【答案】:D
(2)若集合A=(a,,1)又可表示为{a2,a+b,0},求a2018+b2019的值.
【答案】:∵a≠0,∴=0,∴b=0,∴a=﹣1,
∴a2018+b2019=(﹣1)2018+02019=1.
(3)若A={x|﹣2≤x≤3},B={x|2m﹣1≤x≤m+1},
(1)当B A时,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
【答案】:(1)B A,若B= ,则2m﹣1>m+1,∴m>2;
若B≠ ,则,解得;
∴实数m的取值范围是;
(2)根据已知条件知:A∩B= ;
∴若B= ,由(1)知,m>2;
若B≠ ,则,解得m<﹣3;
∴实数m的取值范围为(﹣∞,﹣3)∪(2,+∞).
本节课从实例入手,非常自然贴切地引出子集、真子集、空集、相等的概念及符号;并用Venn图直观地把这种关系表示出来;注意包含与属于符号的运用。
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
