北师大版七年级数学上册2.11有理数的混合运算 解答专项练习 (含答案)
文档属性
| 名称 | 北师大版七年级数学上册2.11有理数的混合运算 解答专项练习 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 88.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览



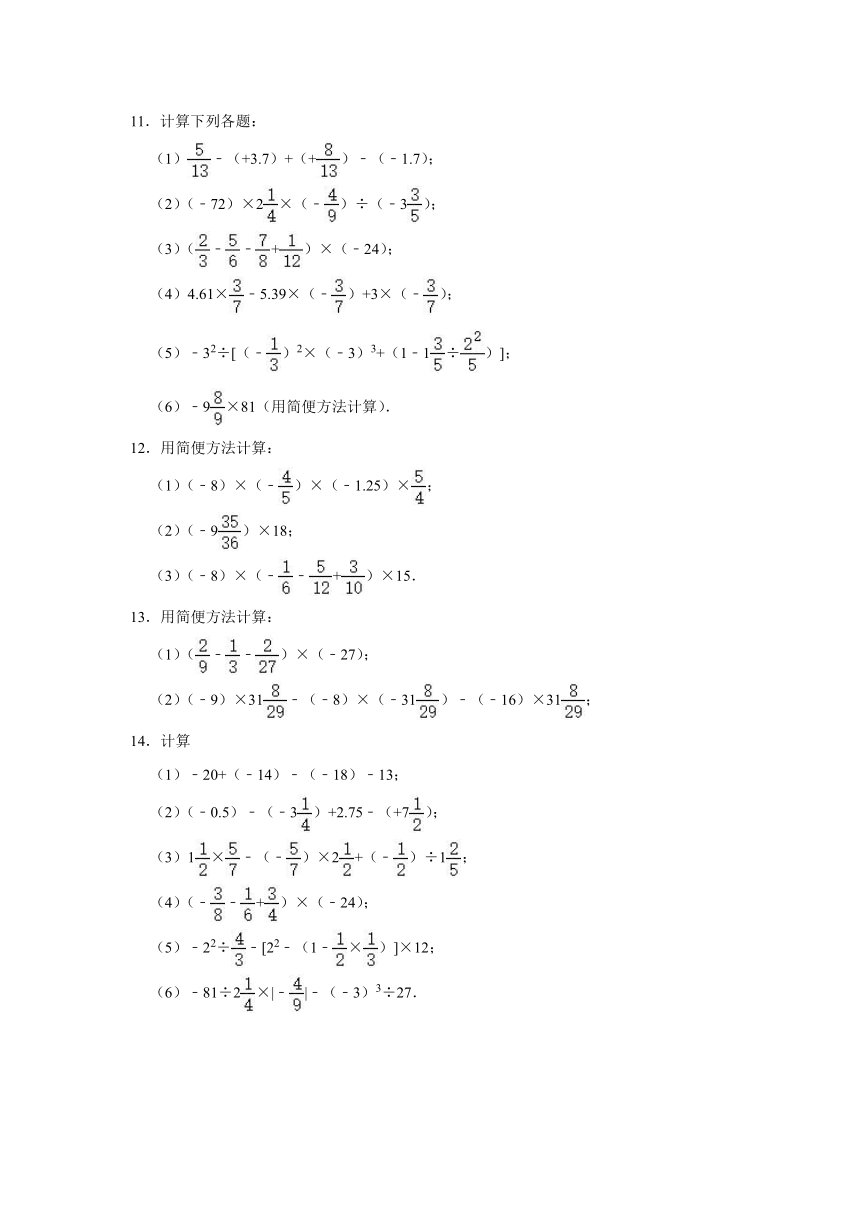
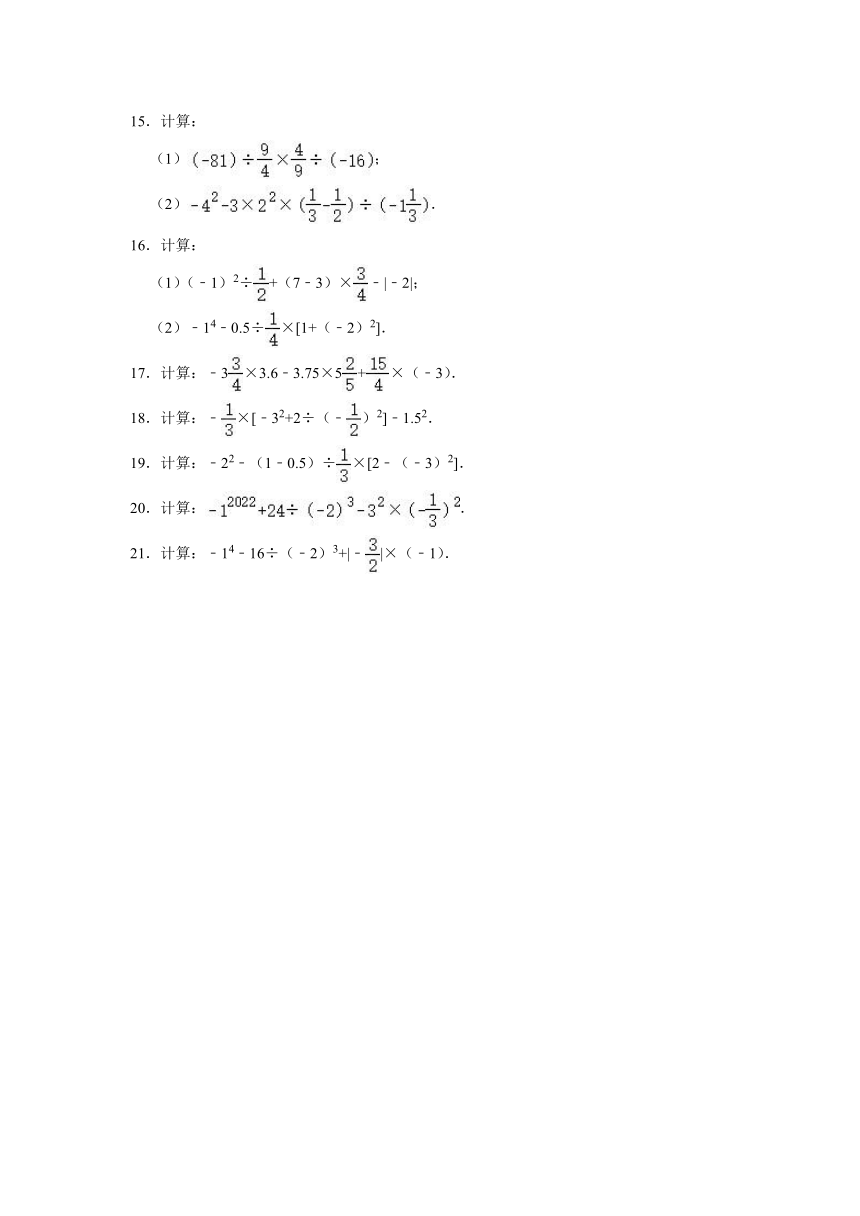
文档简介
2022-2023学年北师大版七年级数学上册《2.11有理数的混合运算》解答专项练习(附答案)
1.北大登山队以二号营地为基准,开始向距二号营地500米的顶峰冲击,他们记向上为正,行进过程记录如下:(单位:米):+150,﹣35,﹣40,+210,﹣32,+20,﹣18,﹣5,+20,+85,﹣25.
(1)他们最终有没有登上顶峰?若没有,距顶峰还有多少米?
(2)登山时,若5名队员在记录的行进路线上都使用了氧气,且每人每米要消耗氧气0.05升,则他们共耗氧多少升?
2.在某次抗险救灾中,消防官兵的冲锋舟沿东西方向的河流营救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:km):
+15,﹣10,+9,﹣8,+14,﹣7,+11,﹣6.
(1)通过计算说明B地在A地的什么方向,与A地相距多远?
(2)救灾过程中,最远处离出发点A有 km;
(3)若冲锋舟每千米耗油0.6升,油箱原有油量为40升,则途中至少还需补充多少升油?
3.某电商把脐橙产品放到了网上售卖,原计划每天卖200kg脐橙,但由于种种原因,实际每天的销售与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负,单位:kg).
星期 一 二 三 四 五 六 日
与计划量的差值 +6 +3 ﹣2 +12 ﹣7 +19 ﹣11
(1)根据表中的数据可知前三天共卖出 kg脐橙;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 kg脐橙;
(3)若电商以1.5元/kg的价格购进脐橙,又按3.5元/kg出售脐橙,且电商需为买家按0.5元/kg的价格支付脐橙的运费,则电商本周一共赚了多少元?
4.某水果店以每箱200元的价格从水果批发市场购进20箱樱桃,若以每箱净重10千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下表:
与标准重量的差值(单位:千克) ﹣0.5 ﹣0.25 0 0.25 0.3 0.5
箱数 1 2 4 6 n 2
(1)求n的值及这20箱樱桃的总重量:
(2)若水果店打算以每千克25元销售这批樱桃,若全部售出可获利多少元;
(3)实际上该水果店第一天以(2)中的价格只销售了这批樱桃的60%,第二天因为害怕剩余樱桃腐烂,决定降价把剩余的樱桃以原零售价的70%全部售出,水果店在销售这批樱桃过程中是盈利还是亏损,盈利或亏损多少元.
5.国庆黄金周电影《长津湖》成为了浙江人民观影的首选,宁波某区9月30日该电影票的售票量为1.1万张,该区10月1日到10月7日售票量的变化如下表(正号表示售票量比前一天多,负号表示售票量比前一天少):
日期 1日 2日 3日 4日 5日 6日 7日
售票量的变化(单位:万张) +0.5 +0.1 ﹣0.3 ﹣0.2 +0.4 ﹣0.2 +0.1
请根据以上信息,回答下列问题:
(1)10月2日的售票量为多少万张?
(2)10月7日与9月30日相比较,哪一天的售票量多?多多少万张?
(3)若平均每张票价为50元,则10月1日到10月7日该区销售《长津湖》电影票共收入多少万元?
6.某公路养护小组乘车沿东西向公路巡视维护.某天早晨从A地出发,最后收工时到达B地.约定向东为正方向,当天的行驶记录如下(单位:千米):+12,﹣14,+13,﹣10,﹣8,+7,﹣16,+8.
(1)问B地在A地的哪个方向?它们相距多少千米?
(2)若汽车行驶每千米耗油0.5升,当天每升汽油7.5元,求该天共耗油费用是多少?
7.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但受种种因素影响,实际每天的生产量与计划量相比有出入,如表记录了该厂某周的生产情况(单位:辆),其中,超过计划量记为正,少于计划量记为负.
星期一 星期二 星期三 星期四 星期五 星期六 星期日
生产情况 +5 ﹣2 ﹣4 +13 ﹣10 +16 ﹣9
(1)该厂这周实际生产自行车多少辆?
(2)该厂实行计件工资制,工人每生产一辆自行车可得60元,若超额完成任务,则每超出一辆另奖15元.该厂工人这一周的工资总额是多少元?
8.某面粉加工厂加工的面粉,用每袋可装10kg面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下表:
与标准质量的偏差(kg) ﹣1.5 ﹣1 ﹣0.5 0 0.5 1 2
袋数(袋) 40 30 10 25 40 20 35
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
9.食品厂为检测某袋装食品的质量是否符合标准,从袋装食品中抽出样品30袋,每袋以100克为标准质量,超过和不足100克的部分分别用正、负数表示,记录如表:
与标准质量的差值/克 ﹣4 ﹣2 0 1 2 3
袋数 3 4 6 8 6 3
(1)在抽测的样品中,任意挑选两袋,它们的质量最大相差多少克?
(2)食品袋中标有“净重100±2克”,这批抽样食品中共有几袋质量合格?请你计算出这30袋食品的合格率;
(3)这批样品的平均质量比每袋的标准质量多(或少)多少克?
10.某批发商于上周日买进某产品10000kg,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000kg该品种的产品,每个摊位的市场管理价为每天20元.如表为本周内该产品每天的批发价格比前一天的涨跌情况.(涨记为正,跌记为负,上周日当天的售价刚好为每千克2.4元)
星期 一 二 三 四 五
与前一天相比价格的涨跌情况/元 +0.3 ﹣0.1 +0.25 +0.2 ﹣0.5
当天的交易量/kg 2500 2000 3000 1500 1000
(1)星期四该产品价格为每千克多少元?
(2)本周内该产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)该批发商在销售过程中采用逐步减少摊位个数(每天减少一个)的方法来降低成本,增加收益,请你帮他算一算,这样他在本周的买卖中共赚了多少钱?
11.计算下列各题:
(1)﹣(+3.7)+(+)﹣(﹣1.7);
(2)(﹣72)×2×(﹣)÷(﹣3);
(3)(﹣﹣+)×(﹣24);
(4)4.61×﹣5.39×(﹣)+3×(﹣);
(5)﹣32÷[(﹣)2×(﹣3)3+(1﹣1÷)];
(6)﹣9×81(用简便方法计算).
12.用简便方法计算:
(1)(﹣8)×(﹣)×(﹣1.25)×;
(2)(﹣9)×18;
(3)(﹣8)×(﹣﹣+)×15.
13.用简便方法计算:
(1)(﹣﹣)×(﹣27);
(2)(﹣9)×31﹣(﹣8)×(﹣31)﹣(﹣16)×31;
14.计算
(1)﹣20+(﹣14)﹣(﹣18)﹣13;
(2)(﹣0.5)﹣(﹣3)+2.75﹣(+7);
(3)1×﹣(﹣)×2+(﹣)÷1;
(4)(﹣﹣+)×(﹣24);
(5)﹣22÷﹣[22﹣(1﹣×)]×12;
(6)﹣81÷2×|﹣|﹣(﹣3)3÷27.
15.计算:
(1);
(2).
16.计算:
(1)(﹣1)2÷+(7﹣3)×﹣|﹣2|;
(2)﹣14﹣0.5÷×[1+(﹣2)2].
17.计算:﹣3×3.6﹣3.75×5+×(﹣3).
18.计算:﹣×[﹣32+2÷(﹣)2]﹣1.52.
19.计算:﹣22﹣(1﹣0.5)÷×[2﹣(﹣3)2].
20.计算:.
21.计算:﹣14﹣16÷(﹣2)3+|﹣|×(﹣1).
参考答案
1.解:(1)+150﹣35﹣40+210﹣32+20﹣18﹣5+20+85﹣25=330(米),
500﹣330=170(米).
答:他们最终没有登顶,距顶峰还有170米;
(2)(+150+|﹣35|+|﹣40|+210+|﹣32|+20+|﹣18|+|﹣5|+20+85+|﹣25|)×(5×0.05)
=640×0.25
=160(升).
答:他们共耗氧气160升.
2.解:(1)∵15﹣10+9﹣8+14﹣7+11﹣6=18>0,
∴B地在A地的东边18千米处;
(2)∵路程记录中各点离出发点的距离分别为:
15千米;
15﹣10=5(千米);
5+9=14(千米);
14﹣8=6(千米);
6+14=20(千米);
20﹣7=13(千米);
13+11=24(千米);
24﹣6=18(千米).
∴最远处离出发点24千米;
故答案为:24;
(3)∵这一天走的总路程为:
15+|﹣10|+9+|﹣8|+14+|﹣7|+11+|﹣6|=80千米,
应耗油80×0.6=48(升),
∴还需补充的油量为:48﹣40=8(升).
答:途中至少还需补充8升油.
3.解:(1)前三天共卖出的脐橙为200×3+(6+3﹣2)=600+7=607(千克);
(2)销售量最多的一天比销售量最少的一天多销售19﹣(﹣11)=30(千克);
(3)200×7+(6+3﹣2+12﹣7+19﹣11)=1420(千克),
1420×(3.5﹣1.5﹣0.5)=2130(元),
答:电商本周一共赚了2130元.
4.解:(1)n=20﹣1﹣2﹣4﹣6﹣2=5(箱),
10×20+(﹣0.5)×1+(﹣0.25)×2+0.25×6+0.3×5+0.5×2
=203(千克);
答:n的值是5,这20箱樱桃的总重量是203千克;
(2)25×203﹣200×20
=1075(元);
答:全部售出可获利1075元;
(3)25×203×60%+25×203×(1﹣60%)×70%﹣200×20
=466(元).
答:是盈利的,盈利466元.
5.解:(1)10月2日的售票量为:1.1+0.5+0.1=1.7(万张);
(2)10月1日的售票量为:1.1+0.5=1.6(万张);
10月2日的售票量为:1.6+0.1=1.7(万张);
10月3日的售票量为:1.7﹣0.3=1.4(万张);
10月4日的售票量为:1.4﹣0.2=1.2(万张);
10月5日的售票量为:1.2+0.4=1.6(万张);
10月6日的售票量为:1.6﹣0.2=1.4(万张);
10月7日的售票量为:1.4+0.1=1.5(万张);
1.7﹣1.1=0.6(万张);
答:10月7日与9月30日相比较,10月2的售票量多,多0.6万张;
(3)10月1日到7日的售票量为:1.6+1.7+1.4+1.2+1.6+1.4+1.5=10.4(万张),
50×10.4=520(万元),
故该区销售《长津湖》共520万元.
6.解:(1)将行驶记录所有的数据相加,
+12﹣14+13﹣10﹣8+7﹣16+8=﹣8,
∵约定向东为正方向,
∴B地在A地的西边,它们相距8千米.
(2)该天汽车总行程为+12+14+13+10+8+7+16+8=88(千米),
∴该天共耗油=88×0.5×7.5=330(元),
答:该天共耗油费用是330元.
7.解:(1)1400+(+5)+(﹣2)+(﹣4)+(+13)+(﹣10)+(+16)+(﹣9)=1409(辆)
答:该厂这周实际生产自行车1409辆.
(2)1409×60+(1409﹣1400)×15=84675(元)
答:该厂工人这一周的工资总额是84675元.
8.解:(1)﹣1.5×40﹣1×30﹣0.5×10+0×25+0.5×40+1×20+2×35=15(kg),
15+200×10=2015(kg).
即这批面粉的总质量为2015kg;
(2)∵100kg小麦加工80kg面粉,
∴加工1kg的面粉需要的小麦数为=1.25(kg),
∴1.25×2015=2518.75(kg).
即这批面粉是由2518.75千克小麦加工的.
9.解:(1)3﹣(﹣4)=7(克).
答:它们的质量相差最大7克.
(2)合格有:4+6+8+6=24(袋),
24÷30×100%=80%,
答:这批抽样食品中共有24袋质量合格,合格率为:80%.
(3)(﹣4)×3+(﹣2)×4+0×6+1×8+2×6+3×3=9(克),
9÷30=0.3(克),
答:这批样品的平均质量比每袋的标准质量多0.3克.
10.解:(1)2.4+0.3﹣0.1+0.25+0.2=3.05(元);
答:星期四该产品价格为每千克3.05元;
(2)星期一的价格是:2.4+0.3=2.7(元);
星期二的价格是:2.7﹣0.1=2.6(元);
星期三的价格是:2.6+0.25=2.85(元);
星期四是:2.85+0.2=3.05(元);
星期五是:3.05﹣0.5=2.55(元);
因而本周内该农产品的最高价格为每斤3.05元,最低价格为每斤2.55元;
(3)(2500×2.7﹣5×20)+(2000×2.6﹣4×20)+(3000×2.85﹣3×20)+(1500×3.05﹣2×20)+(1000×2.55﹣20)﹣10000×2.4
=6650+5120+8490+4535+2530﹣24000
=27325﹣24000
=3325(元).
答:他在本周的买卖中共赚了3325元钱.
11.解:(1)原式=﹣3.7++1.7
=(+)+(﹣3.7+1.7)
=1+(﹣2)
=﹣1;
(2)原式=﹣72×××
=﹣20;
(3)原式=×(﹣24)﹣×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+20+21﹣2
=23;
(4)原式=×(4.61+5.39﹣3)
=×7
=3;
(5)原式=﹣9÷(﹣×27+1﹣÷)
=﹣9÷(﹣3+1﹣2)
=﹣9÷(﹣4)
=;
(6)原式=(﹣10+)×81
=﹣10×81+×81
=﹣810+9
=﹣801.
12.解:(1)原式=﹣(8×1.25)×(×)
=﹣10×1
=﹣10;
(2)原式=(﹣10+)×18
=﹣10×18+×18
=﹣180+
=﹣179;
(3)原式=(﹣8×15)×(﹣﹣+)
=(﹣120)×(﹣﹣+)
=﹣120×(﹣)﹣120×(﹣)﹣120×
=20+50﹣36
=34.
13.解:(1)原式=﹣×27+×27+×27
=﹣6+9+2
=5;
(2)原式=×(﹣9﹣8+16)
=×(﹣1)
=﹣.
14.解:(1)原式=﹣20﹣14+18﹣13
=﹣29;
(2)原式=﹣0.5+3.25+2.75﹣7.5
=﹣2;
(3)原式=1×+×2+(﹣)×
=×(1+2﹣)
=×
=;
(4)原式=﹣×(﹣24)﹣×(﹣24)+×(﹣24)
=9+4﹣18
=﹣5;
(5)原式=﹣4×﹣(4﹣1+)×12
=﹣3﹣×12
=﹣3﹣38
=﹣41;
(6)原式=﹣81××﹣(﹣27)÷27
=﹣16+1
=﹣15.
15.解:(1)原式=81×××
=1;
(2)原式=﹣16﹣3×4×(﹣)×(﹣)
=﹣16﹣12××
=﹣16﹣
=﹣17.
16.解:(1)(﹣1)2÷+(7﹣3)×﹣|﹣2|
=1×2+4×﹣2
=2+3﹣2
=5﹣2
=3;
(2)﹣14﹣0.5÷×[1+(﹣2)2]
=﹣1﹣0.5×4×(1+4)
=﹣1﹣0.5×4×5
=﹣1﹣10
=﹣11.
17.解:﹣3×3.6﹣3.75×5+×(﹣3)
=﹣3.75×3.6﹣3.75×5.4﹣3.75×3
=﹣3.75×(3.6+5.4+3)
=﹣3.75×12
=﹣45.
18.解:原式=﹣×(﹣9+2÷)﹣
=﹣×(﹣9+8)﹣
=﹣×(﹣1)﹣
=﹣
=﹣.
19.解:原式=﹣4﹣÷×(2﹣9)
=﹣4﹣÷×(﹣7)
=﹣4﹣×3×(﹣7)
=﹣4+
=.
20.解:
=﹣1+24÷(﹣8)﹣9×
=﹣1+(﹣3)﹣1
=﹣5.
21.解:原式=﹣1﹣16÷(﹣8)+×(﹣1)
=﹣1+2﹣
=﹣.
1.北大登山队以二号营地为基准,开始向距二号营地500米的顶峰冲击,他们记向上为正,行进过程记录如下:(单位:米):+150,﹣35,﹣40,+210,﹣32,+20,﹣18,﹣5,+20,+85,﹣25.
(1)他们最终有没有登上顶峰?若没有,距顶峰还有多少米?
(2)登山时,若5名队员在记录的行进路线上都使用了氧气,且每人每米要消耗氧气0.05升,则他们共耗氧多少升?
2.在某次抗险救灾中,消防官兵的冲锋舟沿东西方向的河流营救灾民,早晨从A地出发,晚上到达B地,约定向东为正方向,当天的航行路程记录如下(单位:km):
+15,﹣10,+9,﹣8,+14,﹣7,+11,﹣6.
(1)通过计算说明B地在A地的什么方向,与A地相距多远?
(2)救灾过程中,最远处离出发点A有 km;
(3)若冲锋舟每千米耗油0.6升,油箱原有油量为40升,则途中至少还需补充多少升油?
3.某电商把脐橙产品放到了网上售卖,原计划每天卖200kg脐橙,但由于种种原因,实际每天的销售与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负,单位:kg).
星期 一 二 三 四 五 六 日
与计划量的差值 +6 +3 ﹣2 +12 ﹣7 +19 ﹣11
(1)根据表中的数据可知前三天共卖出 kg脐橙;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 kg脐橙;
(3)若电商以1.5元/kg的价格购进脐橙,又按3.5元/kg出售脐橙,且电商需为买家按0.5元/kg的价格支付脐橙的运费,则电商本周一共赚了多少元?
4.某水果店以每箱200元的价格从水果批发市场购进20箱樱桃,若以每箱净重10千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下表:
与标准重量的差值(单位:千克) ﹣0.5 ﹣0.25 0 0.25 0.3 0.5
箱数 1 2 4 6 n 2
(1)求n的值及这20箱樱桃的总重量:
(2)若水果店打算以每千克25元销售这批樱桃,若全部售出可获利多少元;
(3)实际上该水果店第一天以(2)中的价格只销售了这批樱桃的60%,第二天因为害怕剩余樱桃腐烂,决定降价把剩余的樱桃以原零售价的70%全部售出,水果店在销售这批樱桃过程中是盈利还是亏损,盈利或亏损多少元.
5.国庆黄金周电影《长津湖》成为了浙江人民观影的首选,宁波某区9月30日该电影票的售票量为1.1万张,该区10月1日到10月7日售票量的变化如下表(正号表示售票量比前一天多,负号表示售票量比前一天少):
日期 1日 2日 3日 4日 5日 6日 7日
售票量的变化(单位:万张) +0.5 +0.1 ﹣0.3 ﹣0.2 +0.4 ﹣0.2 +0.1
请根据以上信息,回答下列问题:
(1)10月2日的售票量为多少万张?
(2)10月7日与9月30日相比较,哪一天的售票量多?多多少万张?
(3)若平均每张票价为50元,则10月1日到10月7日该区销售《长津湖》电影票共收入多少万元?
6.某公路养护小组乘车沿东西向公路巡视维护.某天早晨从A地出发,最后收工时到达B地.约定向东为正方向,当天的行驶记录如下(单位:千米):+12,﹣14,+13,﹣10,﹣8,+7,﹣16,+8.
(1)问B地在A地的哪个方向?它们相距多少千米?
(2)若汽车行驶每千米耗油0.5升,当天每升汽油7.5元,求该天共耗油费用是多少?
7.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但受种种因素影响,实际每天的生产量与计划量相比有出入,如表记录了该厂某周的生产情况(单位:辆),其中,超过计划量记为正,少于计划量记为负.
星期一 星期二 星期三 星期四 星期五 星期六 星期日
生产情况 +5 ﹣2 ﹣4 +13 ﹣10 +16 ﹣9
(1)该厂这周实际生产自行车多少辆?
(2)该厂实行计件工资制,工人每生产一辆自行车可得60元,若超额完成任务,则每超出一辆另奖15元.该厂工人这一周的工资总额是多少元?
8.某面粉加工厂加工的面粉,用每袋可装10kg面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下表:
与标准质量的偏差(kg) ﹣1.5 ﹣1 ﹣0.5 0 0.5 1 2
袋数(袋) 40 30 10 25 40 20 35
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?
9.食品厂为检测某袋装食品的质量是否符合标准,从袋装食品中抽出样品30袋,每袋以100克为标准质量,超过和不足100克的部分分别用正、负数表示,记录如表:
与标准质量的差值/克 ﹣4 ﹣2 0 1 2 3
袋数 3 4 6 8 6 3
(1)在抽测的样品中,任意挑选两袋,它们的质量最大相差多少克?
(2)食品袋中标有“净重100±2克”,这批抽样食品中共有几袋质量合格?请你计算出这30袋食品的合格率;
(3)这批样品的平均质量比每袋的标准质量多(或少)多少克?
10.某批发商于上周日买进某产品10000kg,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000kg该品种的产品,每个摊位的市场管理价为每天20元.如表为本周内该产品每天的批发价格比前一天的涨跌情况.(涨记为正,跌记为负,上周日当天的售价刚好为每千克2.4元)
星期 一 二 三 四 五
与前一天相比价格的涨跌情况/元 +0.3 ﹣0.1 +0.25 +0.2 ﹣0.5
当天的交易量/kg 2500 2000 3000 1500 1000
(1)星期四该产品价格为每千克多少元?
(2)本周内该产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)该批发商在销售过程中采用逐步减少摊位个数(每天减少一个)的方法来降低成本,增加收益,请你帮他算一算,这样他在本周的买卖中共赚了多少钱?
11.计算下列各题:
(1)﹣(+3.7)+(+)﹣(﹣1.7);
(2)(﹣72)×2×(﹣)÷(﹣3);
(3)(﹣﹣+)×(﹣24);
(4)4.61×﹣5.39×(﹣)+3×(﹣);
(5)﹣32÷[(﹣)2×(﹣3)3+(1﹣1÷)];
(6)﹣9×81(用简便方法计算).
12.用简便方法计算:
(1)(﹣8)×(﹣)×(﹣1.25)×;
(2)(﹣9)×18;
(3)(﹣8)×(﹣﹣+)×15.
13.用简便方法计算:
(1)(﹣﹣)×(﹣27);
(2)(﹣9)×31﹣(﹣8)×(﹣31)﹣(﹣16)×31;
14.计算
(1)﹣20+(﹣14)﹣(﹣18)﹣13;
(2)(﹣0.5)﹣(﹣3)+2.75﹣(+7);
(3)1×﹣(﹣)×2+(﹣)÷1;
(4)(﹣﹣+)×(﹣24);
(5)﹣22÷﹣[22﹣(1﹣×)]×12;
(6)﹣81÷2×|﹣|﹣(﹣3)3÷27.
15.计算:
(1);
(2).
16.计算:
(1)(﹣1)2÷+(7﹣3)×﹣|﹣2|;
(2)﹣14﹣0.5÷×[1+(﹣2)2].
17.计算:﹣3×3.6﹣3.75×5+×(﹣3).
18.计算:﹣×[﹣32+2÷(﹣)2]﹣1.52.
19.计算:﹣22﹣(1﹣0.5)÷×[2﹣(﹣3)2].
20.计算:.
21.计算:﹣14﹣16÷(﹣2)3+|﹣|×(﹣1).
参考答案
1.解:(1)+150﹣35﹣40+210﹣32+20﹣18﹣5+20+85﹣25=330(米),
500﹣330=170(米).
答:他们最终没有登顶,距顶峰还有170米;
(2)(+150+|﹣35|+|﹣40|+210+|﹣32|+20+|﹣18|+|﹣5|+20+85+|﹣25|)×(5×0.05)
=640×0.25
=160(升).
答:他们共耗氧气160升.
2.解:(1)∵15﹣10+9﹣8+14﹣7+11﹣6=18>0,
∴B地在A地的东边18千米处;
(2)∵路程记录中各点离出发点的距离分别为:
15千米;
15﹣10=5(千米);
5+9=14(千米);
14﹣8=6(千米);
6+14=20(千米);
20﹣7=13(千米);
13+11=24(千米);
24﹣6=18(千米).
∴最远处离出发点24千米;
故答案为:24;
(3)∵这一天走的总路程为:
15+|﹣10|+9+|﹣8|+14+|﹣7|+11+|﹣6|=80千米,
应耗油80×0.6=48(升),
∴还需补充的油量为:48﹣40=8(升).
答:途中至少还需补充8升油.
3.解:(1)前三天共卖出的脐橙为200×3+(6+3﹣2)=600+7=607(千克);
(2)销售量最多的一天比销售量最少的一天多销售19﹣(﹣11)=30(千克);
(3)200×7+(6+3﹣2+12﹣7+19﹣11)=1420(千克),
1420×(3.5﹣1.5﹣0.5)=2130(元),
答:电商本周一共赚了2130元.
4.解:(1)n=20﹣1﹣2﹣4﹣6﹣2=5(箱),
10×20+(﹣0.5)×1+(﹣0.25)×2+0.25×6+0.3×5+0.5×2
=203(千克);
答:n的值是5,这20箱樱桃的总重量是203千克;
(2)25×203﹣200×20
=1075(元);
答:全部售出可获利1075元;
(3)25×203×60%+25×203×(1﹣60%)×70%﹣200×20
=466(元).
答:是盈利的,盈利466元.
5.解:(1)10月2日的售票量为:1.1+0.5+0.1=1.7(万张);
(2)10月1日的售票量为:1.1+0.5=1.6(万张);
10月2日的售票量为:1.6+0.1=1.7(万张);
10月3日的售票量为:1.7﹣0.3=1.4(万张);
10月4日的售票量为:1.4﹣0.2=1.2(万张);
10月5日的售票量为:1.2+0.4=1.6(万张);
10月6日的售票量为:1.6﹣0.2=1.4(万张);
10月7日的售票量为:1.4+0.1=1.5(万张);
1.7﹣1.1=0.6(万张);
答:10月7日与9月30日相比较,10月2的售票量多,多0.6万张;
(3)10月1日到7日的售票量为:1.6+1.7+1.4+1.2+1.6+1.4+1.5=10.4(万张),
50×10.4=520(万元),
故该区销售《长津湖》共520万元.
6.解:(1)将行驶记录所有的数据相加,
+12﹣14+13﹣10﹣8+7﹣16+8=﹣8,
∵约定向东为正方向,
∴B地在A地的西边,它们相距8千米.
(2)该天汽车总行程为+12+14+13+10+8+7+16+8=88(千米),
∴该天共耗油=88×0.5×7.5=330(元),
答:该天共耗油费用是330元.
7.解:(1)1400+(+5)+(﹣2)+(﹣4)+(+13)+(﹣10)+(+16)+(﹣9)=1409(辆)
答:该厂这周实际生产自行车1409辆.
(2)1409×60+(1409﹣1400)×15=84675(元)
答:该厂工人这一周的工资总额是84675元.
8.解:(1)﹣1.5×40﹣1×30﹣0.5×10+0×25+0.5×40+1×20+2×35=15(kg),
15+200×10=2015(kg).
即这批面粉的总质量为2015kg;
(2)∵100kg小麦加工80kg面粉,
∴加工1kg的面粉需要的小麦数为=1.25(kg),
∴1.25×2015=2518.75(kg).
即这批面粉是由2518.75千克小麦加工的.
9.解:(1)3﹣(﹣4)=7(克).
答:它们的质量相差最大7克.
(2)合格有:4+6+8+6=24(袋),
24÷30×100%=80%,
答:这批抽样食品中共有24袋质量合格,合格率为:80%.
(3)(﹣4)×3+(﹣2)×4+0×6+1×8+2×6+3×3=9(克),
9÷30=0.3(克),
答:这批样品的平均质量比每袋的标准质量多0.3克.
10.解:(1)2.4+0.3﹣0.1+0.25+0.2=3.05(元);
答:星期四该产品价格为每千克3.05元;
(2)星期一的价格是:2.4+0.3=2.7(元);
星期二的价格是:2.7﹣0.1=2.6(元);
星期三的价格是:2.6+0.25=2.85(元);
星期四是:2.85+0.2=3.05(元);
星期五是:3.05﹣0.5=2.55(元);
因而本周内该农产品的最高价格为每斤3.05元,最低价格为每斤2.55元;
(3)(2500×2.7﹣5×20)+(2000×2.6﹣4×20)+(3000×2.85﹣3×20)+(1500×3.05﹣2×20)+(1000×2.55﹣20)﹣10000×2.4
=6650+5120+8490+4535+2530﹣24000
=27325﹣24000
=3325(元).
答:他在本周的买卖中共赚了3325元钱.
11.解:(1)原式=﹣3.7++1.7
=(+)+(﹣3.7+1.7)
=1+(﹣2)
=﹣1;
(2)原式=﹣72×××
=﹣20;
(3)原式=×(﹣24)﹣×(﹣24)﹣×(﹣24)+×(﹣24)
=﹣16+20+21﹣2
=23;
(4)原式=×(4.61+5.39﹣3)
=×7
=3;
(5)原式=﹣9÷(﹣×27+1﹣÷)
=﹣9÷(﹣3+1﹣2)
=﹣9÷(﹣4)
=;
(6)原式=(﹣10+)×81
=﹣10×81+×81
=﹣810+9
=﹣801.
12.解:(1)原式=﹣(8×1.25)×(×)
=﹣10×1
=﹣10;
(2)原式=(﹣10+)×18
=﹣10×18+×18
=﹣180+
=﹣179;
(3)原式=(﹣8×15)×(﹣﹣+)
=(﹣120)×(﹣﹣+)
=﹣120×(﹣)﹣120×(﹣)﹣120×
=20+50﹣36
=34.
13.解:(1)原式=﹣×27+×27+×27
=﹣6+9+2
=5;
(2)原式=×(﹣9﹣8+16)
=×(﹣1)
=﹣.
14.解:(1)原式=﹣20﹣14+18﹣13
=﹣29;
(2)原式=﹣0.5+3.25+2.75﹣7.5
=﹣2;
(3)原式=1×+×2+(﹣)×
=×(1+2﹣)
=×
=;
(4)原式=﹣×(﹣24)﹣×(﹣24)+×(﹣24)
=9+4﹣18
=﹣5;
(5)原式=﹣4×﹣(4﹣1+)×12
=﹣3﹣×12
=﹣3﹣38
=﹣41;
(6)原式=﹣81××﹣(﹣27)÷27
=﹣16+1
=﹣15.
15.解:(1)原式=81×××
=1;
(2)原式=﹣16﹣3×4×(﹣)×(﹣)
=﹣16﹣12××
=﹣16﹣
=﹣17.
16.解:(1)(﹣1)2÷+(7﹣3)×﹣|﹣2|
=1×2+4×﹣2
=2+3﹣2
=5﹣2
=3;
(2)﹣14﹣0.5÷×[1+(﹣2)2]
=﹣1﹣0.5×4×(1+4)
=﹣1﹣0.5×4×5
=﹣1﹣10
=﹣11.
17.解:﹣3×3.6﹣3.75×5+×(﹣3)
=﹣3.75×3.6﹣3.75×5.4﹣3.75×3
=﹣3.75×(3.6+5.4+3)
=﹣3.75×12
=﹣45.
18.解:原式=﹣×(﹣9+2÷)﹣
=﹣×(﹣9+8)﹣
=﹣×(﹣1)﹣
=﹣
=﹣.
19.解:原式=﹣4﹣÷×(2﹣9)
=﹣4﹣÷×(﹣7)
=﹣4﹣×3×(﹣7)
=﹣4+
=.
20.解:
=﹣1+24÷(﹣8)﹣9×
=﹣1+(﹣3)﹣1
=﹣5.
21.解:原式=﹣1﹣16÷(﹣8)+×(﹣1)
=﹣1+2﹣
=﹣.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
