华东师大版九年级数学上册23.4中位线 解答专项练习题(含答案)
文档属性
| 名称 | 华东师大版九年级数学上册23.4中位线 解答专项练习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 566.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 21:51:57 | ||
图片预览


文档简介
2022-2023学年华东师大版九年级数学上册《23.4中位线》解答专项练习题(附答案)
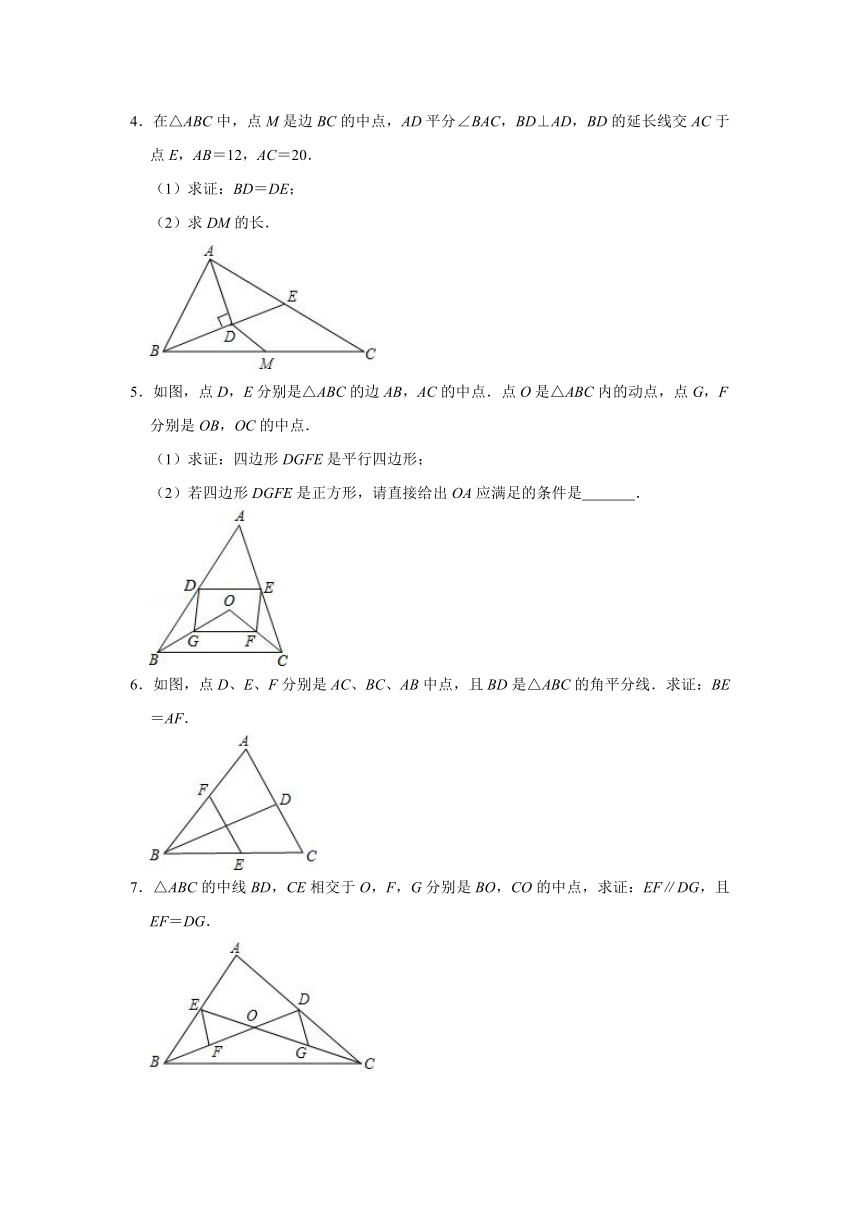
1.如图,△ABC中,AD平分∠BAC,AD⊥BD,E为BC的中点.
(1)求证:DE∥AC;
(2)若AB=4,AC=6,求DE的长.
2.在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
(1)试说明AF与DE互相平分;
(2)若AB=8,BC=12,求DO的长.
3.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
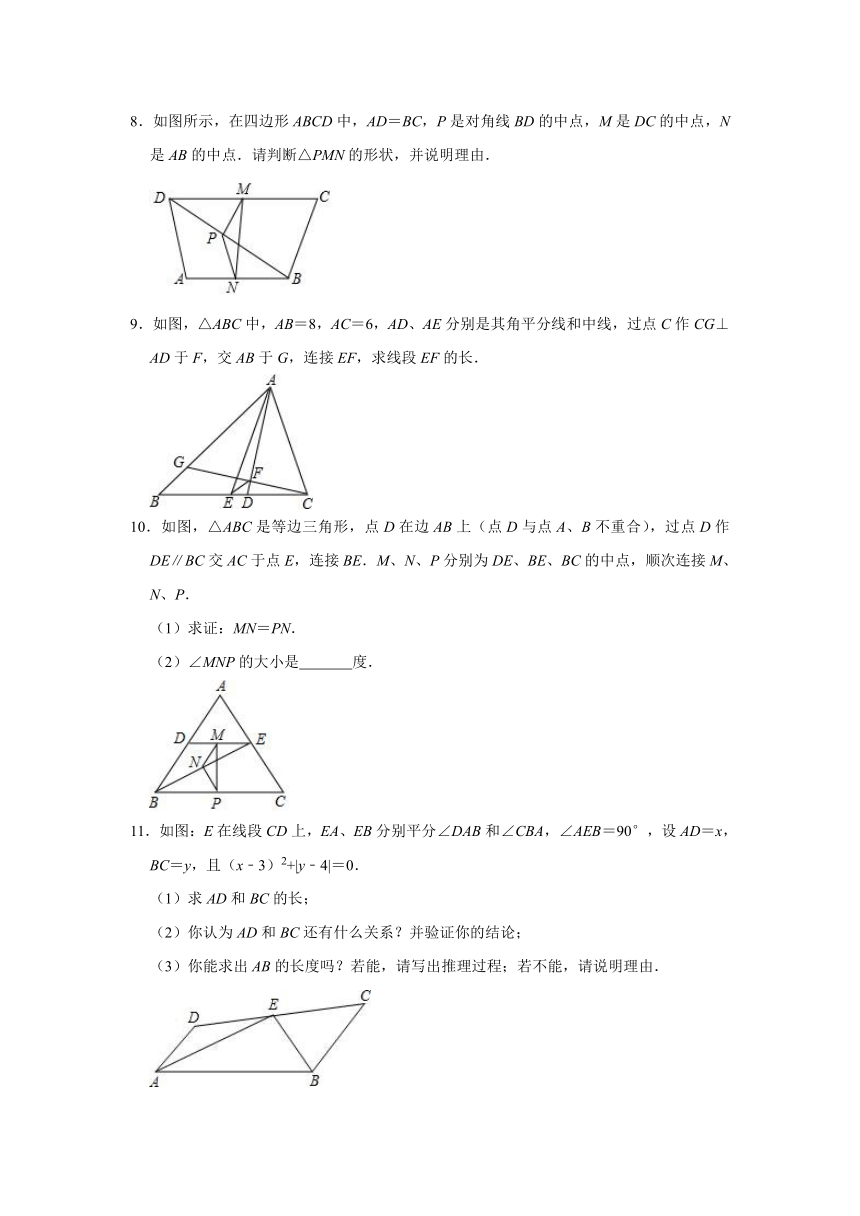
4.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
5.如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是正方形,请直接给出OA应满足的条件是 .
6.如图,点D、E、F分别是AC、BC、AB中点,且BD是△ABC的角平分线.求证:BE=AF.
7.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
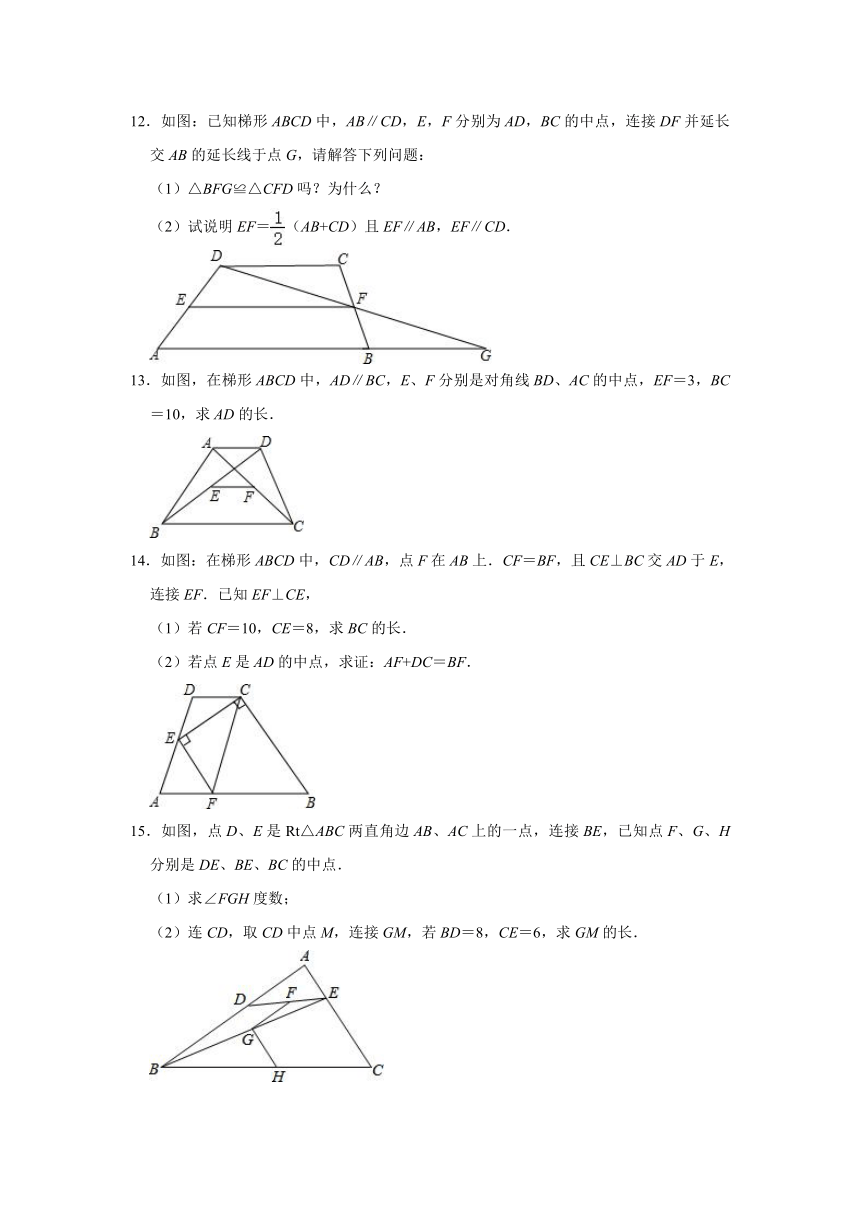
8.如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.
9.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
10.如图,△ABC是等边三角形,点D在边AB上(点D与点A、B不重合),过点D作DE∥BC交AC于点E,连接BE.M、N、P分别为DE、BE、BC的中点,顺次连接M、N、P.
(1)求证:MN=PN.
(2)∠MNP的大小是 度.
11.如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x﹣3)2+|y﹣4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
12.如图:已知梯形ABCD中,AB∥CD,E,F分别为AD,BC的中点,连接DF并延长交AB的延长线于点G,请解答下列问题:
(1)△BFG≌△CFD吗?为什么?
(2)试说明EF=(AB+CD)且EF∥AB,EF∥CD.
13.如图,在梯形ABCD中,AD∥BC,E、F分别是对角线BD、AC的中点,EF=3,BC=10,求AD的长.
14.如图:在梯形ABCD中,CD∥AB,点F在AB上.CF=BF,且CE⊥BC交AD于E,连接EF.已知EF⊥CE,
(1)若CF=10,CE=8,求BC的长.
(2)若点E是AD的中点,求证:AF+DC=BF.
15.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
16.已知:如图,在△ABC中,AD平分∠BAC,CN⊥AD于E交AB于N,F是AC的中点,FE的延长线交BC于M.试判断BM=MC的正确性.如果正确,请给出证明过程;若不正确,请说明理由.
17.如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.
求证:(1)DE∥BC;(2).
18.如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
19.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
20.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
21.已知:点D、E分别是△ABC的边BC、AC边的中点.
(1)如图①,若AB=10,求DE的长;
(2)如图②,点F是边AB上一点,FG∥AD,交ED的延长线于点G,求证:AF=DG.
22.如图1,在△ABC中,点D在边AC上,DB=BC,点E是CD的中点,点F是AB的中点.
(1)求证:EF=AB.
(2)如图2,在△ABC外作∠EAG=∠FEA,交BE的延长线于点G,求证:△ABE≌△AGE.
参考答案
1.(1)证明:延长BD交AC于H,
在△ADB和△ADH中,
,
∴△ADB≌△ADH,
∴BD=HD,又E为BC的中点.
∴DE∥AC;
(2)解:∵△ADB≌△ADH,
∴AH=AB=4,
∴CH=AC﹣AH=2,
∵BD=HD,又E为BC的中点,
∴DE=CH=1.
2.解:(1)∵E、F分别是BC、AC的中点,
∴EF是△ABC的中位线,
∴EF∥AB且EF=AB.
又AB=2AD,即AD=AB,
∴AD∥EF,AD=EF,
∴四边形AEFD是平行四边形,
∴AF与DE互相平分;
(2)∵在Rt△ABC中,∠BAC=90°,AB=8,BC=12,
∴由勾股定理得 AC===4
又由(1)知,OA=OF,且AF=CF,
∴OA=AC=.
∴在△AOD中,∠DAO=90°,AD=AB=4,OA=,
∴由勾股定理得 DO===.
3.解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE=BC,
∵CF=BC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD==2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DH=DC=,
∵DE=CF=2,
∴S四边形DEFC=CF DH=2×=2.
4.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
5.(1)证明:∵D、E是AB、AC的中点,
∴DE∥BC且DE=BC,
∵G、F是OB、OC的中点,
∴GF∥BC且GF=BC,
∴DE∥GF且DE=GF,
∴四边形DGFE是平行四边形;
(2)解:AO=BC,AO⊥BC时四边形DGFE是正方形,
理由如下:
∵D、G分别是AB、OB的中点,
∴DG∥AO,DG=AO,
又∵AO=BC,AO⊥BC,
∴DG⊥GF,DG=GF,
∴四边形DGFE正方形,
故答案为:AO=BC,AO⊥BC.
6.证明:连接DE,
∵点D、E、F分别是AC、BC、AB中点.
∴DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF.
7.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
8.解:△PMN是等腰三角形.
理由如下:
∵点P是BD的中点,点M是CD的中点,
∴PM=BC,
同理:PN=AD,
∵AD=BC,
∴PM=PN,
∴△PMN是等腰三角形.
9.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=BG=1.
10.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°.
∵DE∥AB,
∴∠ABC=∠ADE=60°,∠ACB=∠AED=60°.
∴∠ADE=∠AED=60°.
∴△ADE是等边三角形.
∴AD=AE.
∴BD=CE.
∵M、N分别为DE、BE的中点,
∴MN=BD.
∵N、P分别为BE、BC的中点,
∴NP=CE.
∴MN=PN.
(2)∵MN∥BD,
∴∠MNE=∠ABE,
∵∠ENP=∠NBP+∠NPB,
∵PN∥EC,
∴∠NPB=∠C=60°
∴∠MNP=∠MNE+∠ENP=∠ABE+∠EBC+∠NPB=60°+60°=120°,
故答案为:120.
11.解:(1)∵AD=x,BC=y,且(x﹣3)2+|y﹣4|=0,
∴AD=3,BC=4.
(2)AD∥BC,
理由是:∵在△AEB中,∠AEB=90°,
∴∠EAB+∠EBA=90°,
又∵EA、EB分别平分∠DAB和∠CBA,
∴∠DAB+∠ABC=180°.
∴AD∥BC.
(3)能.
如图,过E作EF∥AD,交AB于F,
∵AD∥BC(已证),EF∥AD,
∴AD∥EF∥BC,
则∠DAE=∠AEF,∠EBC=∠BEF,
∵EA、EB分别平分∠DAB和∠CBA,
∴∠EAF=∠AEF,∠EBF=∠BEF,
∴AF=EF=FB,
又∵EF∥AD∥BC,
∴EF是梯形ABCD的中位线,
∴EF==,
∴AB=7.
12.解:(1)△BFG≌△CFD,
∵AB∥CD,
∴∠CDF=∠G,∠C=∠FBG,
在△BFG和△CFD中,
,
∴△BFG≌△CFD;
(2)∵△BFG≌△CFD,
∴BG=CD,
∵E,F分别为AD,BC的中点,
∴EF=AG,EF∥AB,又AB∥CD,
∴EF∥CD,
∴EF=(AB+CD)且EF∥AB,EF∥CD.
13.解:连接AE,并延长交BC于点G,
∵AD∥BC,
∴∠DAE=∠BGE,
∵E是BD中点,
∴DE=BE,
在△ADE和△GBE中,
,
∴△ADE≌△GBE(AAS),
∴BG=AD,AE=EG,
∵F是AC的中点,
∴CG=2EF=2×3=6,
∴AD=BG=BC﹣CG=10﹣6=4.
14.解:(1)过点F作FH⊥BC于点H,
∵CE⊥BC,EF⊥CE,
∴四边形CEFH是矩形,
∴CH=EF,
在Rt△CEF中,CF=10,CE=8,
∴EF=6,
∴CH=6,
∵CF=BF,
∴BC=2CH=12;
(2)连接EH,交CF于点G,
∵四边形CEFH是矩形,
∴CG=GF,EG=GH,
∴EG是梯形ADCF的中位线,GH是△BCF的中位线,
∴EG=(AF+DC),GH=BF,
∴AF+DC=BF.
15.解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EGH=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°﹣∠A=180°﹣90°=90°.
(2)如图所示:连接FM、HM.
∵M、H分别是BC和DC的中点,
∴MH∥BD,MH=.
同理:GF∥BD,GF=.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH==3,,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM==5.
16.解:结论BM=MC正确.
证明过程如下:
∵AD平分∠BAC,
∴∠NAE=∠CAE.
∵CE⊥AD,
∴∠AEN=∠AEC=90°.
∵AE=AE,
∴△ANE≌△ACE.
∴NE=CE.
∵F为AC的中点,
∴AF=CF.
∴EF∥AB.
∵AF=CF,
∴BM=MC.
17.证明:(1)延长AD、AE,交BC于F、G;
∵BE⊥AG,
∴∠AEB=∠BEG=90°;
∵BE平分∠ABG,
∴∠ABE=∠GBE;
∴∠BAE=∠BGE;
∴△ABG是等腰三角形;
∴AB=BG,E是AG中点;
同理可得:AC=CF,D是AF中点;
∴DE是△AFG的中位线;
∴DE∥BC.
(2)由(1)知DE是△AFG的中位线,
∴DE=FG;
∵FG=BG+CF﹣BC,且AB=BG,AC=CF;
∴FG=AB+AC﹣BC,即DE=(AB+AC﹣BC).
18.(1)证明:∵CA=CD,CF平分∠ACB,
∴CF是AD边的中线,
∵E是AB的中点,
∴EF是△ABD的中位线.
∴EF∥BD;
(2)解:∵∠ACB=60°,CA=CD,
∴△CAD是等边三角形,
∴∠ADC=60°,AD=DC=AC=8,
∴BD=BC﹣CD=12﹣8=4,
过点A作AM⊥BC,垂足为M,
∴AM=AD=×8=4,
S△ABD=BD AM=×4×4=8,
∵EF∥BD,
∴=,
∴=,
∴S△AEF=×8=2,
四边形BDFE的面积=S△ABD﹣S△AEF=8﹣2=6.
19.(1)证明:如图1中,
∵AE平分∠BAC,BE⊥AE于点E,
∴△ABD是等腰三角形,
∴BE=DE,
∵BF=FC,
∴EF=DC==(AC﹣AB).
(2)结论:EF=(AB﹣AC),
理由:如图2中,延长AC交BE的延长线于P.
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠APE,
∴AB=AP,
∵AE⊥BP,
∴E为BP的中点,
∴BE=PE,
∵点F为BC的中点,
∴BF=FC,
∴EF=PC=(AP﹣AC)=(AB﹣AC).
20.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC,∴GH∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
21.(1)解:∵点D、E分别是△ABC的边BC、AC边的中点,
∴DE为△ABC的中位线,
∴DE∥AB,DE=AB,
∵AB=10,
∴DE=5;
(2)证明:∵DE∥AB,FG∥AD,
∴四边形AFGD是平行四边形,
∴AF=DG.
22.(1)证明:如图1,∵DB=BC,点E是CD的中点,
∴BE⊥CD,
∴∠AEB=90°,
∵点F是AB的中点,
∴EF=AB.
(2)证明:如图2,∵AF=AB,EF=AB,
∴AF=EF,
∴∠EAB=∠FEA,
∵∠EAG=∠FEA,
∴∠EAB=∠EAG,
∵BE⊥CD,
∴∠AEB=∠AEG=90°,
在△ABE和△AGE中,
,
∴△ABE≌△AGE(ASA).
1.如图,△ABC中,AD平分∠BAC,AD⊥BD,E为BC的中点.
(1)求证:DE∥AC;
(2)若AB=4,AC=6,求DE的长.
2.在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
(1)试说明AF与DE互相平分;
(2)若AB=8,BC=12,求DO的长.
3.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
4.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
5.如图,点D,E分别是△ABC的边AB,AC的中点.点O是△ABC内的动点,点G,F分别是OB,OC的中点.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是正方形,请直接给出OA应满足的条件是 .
6.如图,点D、E、F分别是AC、BC、AB中点,且BD是△ABC的角平分线.求证:BE=AF.
7.△ABC的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证:EF∥DG,且EF=DG.
8.如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.
9.如图,△ABC中,AB=8,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
10.如图,△ABC是等边三角形,点D在边AB上(点D与点A、B不重合),过点D作DE∥BC交AC于点E,连接BE.M、N、P分别为DE、BE、BC的中点,顺次连接M、N、P.
(1)求证:MN=PN.
(2)∠MNP的大小是 度.
11.如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x﹣3)2+|y﹣4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
12.如图:已知梯形ABCD中,AB∥CD,E,F分别为AD,BC的中点,连接DF并延长交AB的延长线于点G,请解答下列问题:
(1)△BFG≌△CFD吗?为什么?
(2)试说明EF=(AB+CD)且EF∥AB,EF∥CD.
13.如图,在梯形ABCD中,AD∥BC,E、F分别是对角线BD、AC的中点,EF=3,BC=10,求AD的长.
14.如图:在梯形ABCD中,CD∥AB,点F在AB上.CF=BF,且CE⊥BC交AD于E,连接EF.已知EF⊥CE,
(1)若CF=10,CE=8,求BC的长.
(2)若点E是AD的中点,求证:AF+DC=BF.
15.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
16.已知:如图,在△ABC中,AD平分∠BAC,CN⊥AD于E交AB于N,F是AC的中点,FE的延长线交BC于M.试判断BM=MC的正确性.如果正确,请给出证明过程;若不正确,请说明理由.
17.如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.
求证:(1)DE∥BC;(2).
18.如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
(1)求证:EF∥BD;
(2)若∠ACB=60°,AC=8,BC=12,求四边形BDFE的面积.
19.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
20.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
21.已知:点D、E分别是△ABC的边BC、AC边的中点.
(1)如图①,若AB=10,求DE的长;
(2)如图②,点F是边AB上一点,FG∥AD,交ED的延长线于点G,求证:AF=DG.
22.如图1,在△ABC中,点D在边AC上,DB=BC,点E是CD的中点,点F是AB的中点.
(1)求证:EF=AB.
(2)如图2,在△ABC外作∠EAG=∠FEA,交BE的延长线于点G,求证:△ABE≌△AGE.
参考答案
1.(1)证明:延长BD交AC于H,
在△ADB和△ADH中,
,
∴△ADB≌△ADH,
∴BD=HD,又E为BC的中点.
∴DE∥AC;
(2)解:∵△ADB≌△ADH,
∴AH=AB=4,
∴CH=AC﹣AH=2,
∵BD=HD,又E为BC的中点,
∴DE=CH=1.
2.解:(1)∵E、F分别是BC、AC的中点,
∴EF是△ABC的中位线,
∴EF∥AB且EF=AB.
又AB=2AD,即AD=AB,
∴AD∥EF,AD=EF,
∴四边形AEFD是平行四边形,
∴AF与DE互相平分;
(2)∵在Rt△ABC中,∠BAC=90°,AB=8,BC=12,
∴由勾股定理得 AC===4
又由(1)知,OA=OF,且AF=CF,
∴OA=AC=.
∴在△AOD中,∠DAO=90°,AD=AB=4,OA=,
∴由勾股定理得 DO===.
3.解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE=BC,
∵CF=BC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD==2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DH=DC=,
∵DE=CF=2,
∴S四边形DEFC=CF DH=2×=2.
4.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DM=EC=4.
5.(1)证明:∵D、E是AB、AC的中点,
∴DE∥BC且DE=BC,
∵G、F是OB、OC的中点,
∴GF∥BC且GF=BC,
∴DE∥GF且DE=GF,
∴四边形DGFE是平行四边形;
(2)解:AO=BC,AO⊥BC时四边形DGFE是正方形,
理由如下:
∵D、G分别是AB、OB的中点,
∴DG∥AO,DG=AO,
又∵AO=BC,AO⊥BC,
∴DG⊥GF,DG=GF,
∴四边形DGFE正方形,
故答案为:AO=BC,AO⊥BC.
6.证明:连接DE,
∵点D、E、F分别是AC、BC、AB中点.
∴DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF.
7.证明:连接DE,FG,
∵BD,CE是△ABC的中线,
∴D,E是AB,AC的中点,
∴DE∥BC,DE=BC,
同理:FG∥BC,FG=BC,
∴DE∥FG,DE=FG,
∴四边形DEFG是平行四边形,
∴EF∥DG,EF=DG.
8.解:△PMN是等腰三角形.
理由如下:
∵点P是BD的中点,点M是CD的中点,
∴PM=BC,
同理:PN=AD,
∵AD=BC,
∴PM=PN,
∴△PMN是等腰三角形.
9.解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB﹣AG=8﹣6=2.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=BG=1.
10.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠ABC=∠ACB=60°.
∵DE∥AB,
∴∠ABC=∠ADE=60°,∠ACB=∠AED=60°.
∴∠ADE=∠AED=60°.
∴△ADE是等边三角形.
∴AD=AE.
∴BD=CE.
∵M、N分别为DE、BE的中点,
∴MN=BD.
∵N、P分别为BE、BC的中点,
∴NP=CE.
∴MN=PN.
(2)∵MN∥BD,
∴∠MNE=∠ABE,
∵∠ENP=∠NBP+∠NPB,
∵PN∥EC,
∴∠NPB=∠C=60°
∴∠MNP=∠MNE+∠ENP=∠ABE+∠EBC+∠NPB=60°+60°=120°,
故答案为:120.
11.解:(1)∵AD=x,BC=y,且(x﹣3)2+|y﹣4|=0,
∴AD=3,BC=4.
(2)AD∥BC,
理由是:∵在△AEB中,∠AEB=90°,
∴∠EAB+∠EBA=90°,
又∵EA、EB分别平分∠DAB和∠CBA,
∴∠DAB+∠ABC=180°.
∴AD∥BC.
(3)能.
如图,过E作EF∥AD,交AB于F,
∵AD∥BC(已证),EF∥AD,
∴AD∥EF∥BC,
则∠DAE=∠AEF,∠EBC=∠BEF,
∵EA、EB分别平分∠DAB和∠CBA,
∴∠EAF=∠AEF,∠EBF=∠BEF,
∴AF=EF=FB,
又∵EF∥AD∥BC,
∴EF是梯形ABCD的中位线,
∴EF==,
∴AB=7.
12.解:(1)△BFG≌△CFD,
∵AB∥CD,
∴∠CDF=∠G,∠C=∠FBG,
在△BFG和△CFD中,
,
∴△BFG≌△CFD;
(2)∵△BFG≌△CFD,
∴BG=CD,
∵E,F分别为AD,BC的中点,
∴EF=AG,EF∥AB,又AB∥CD,
∴EF∥CD,
∴EF=(AB+CD)且EF∥AB,EF∥CD.
13.解:连接AE,并延长交BC于点G,
∵AD∥BC,
∴∠DAE=∠BGE,
∵E是BD中点,
∴DE=BE,
在△ADE和△GBE中,
,
∴△ADE≌△GBE(AAS),
∴BG=AD,AE=EG,
∵F是AC的中点,
∴CG=2EF=2×3=6,
∴AD=BG=BC﹣CG=10﹣6=4.
14.解:(1)过点F作FH⊥BC于点H,
∵CE⊥BC,EF⊥CE,
∴四边形CEFH是矩形,
∴CH=EF,
在Rt△CEF中,CF=10,CE=8,
∴EF=6,
∴CH=6,
∵CF=BF,
∴BC=2CH=12;
(2)连接EH,交CF于点G,
∵四边形CEFH是矩形,
∴CG=GF,EG=GH,
∴EG是梯形ADCF的中位线,GH是△BCF的中位线,
∴EG=(AF+DC),GH=BF,
∴AF+DC=BF.
15.解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EGH=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°﹣∠A=180°﹣90°=90°.
(2)如图所示:连接FM、HM.
∵M、H分别是BC和DC的中点,
∴MH∥BD,MH=.
同理:GF∥BD,GF=.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH==3,,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM==5.
16.解:结论BM=MC正确.
证明过程如下:
∵AD平分∠BAC,
∴∠NAE=∠CAE.
∵CE⊥AD,
∴∠AEN=∠AEC=90°.
∵AE=AE,
∴△ANE≌△ACE.
∴NE=CE.
∵F为AC的中点,
∴AF=CF.
∴EF∥AB.
∵AF=CF,
∴BM=MC.
17.证明:(1)延长AD、AE,交BC于F、G;
∵BE⊥AG,
∴∠AEB=∠BEG=90°;
∵BE平分∠ABG,
∴∠ABE=∠GBE;
∴∠BAE=∠BGE;
∴△ABG是等腰三角形;
∴AB=BG,E是AG中点;
同理可得:AC=CF,D是AF中点;
∴DE是△AFG的中位线;
∴DE∥BC.
(2)由(1)知DE是△AFG的中位线,
∴DE=FG;
∵FG=BG+CF﹣BC,且AB=BG,AC=CF;
∴FG=AB+AC﹣BC,即DE=(AB+AC﹣BC).
18.(1)证明:∵CA=CD,CF平分∠ACB,
∴CF是AD边的中线,
∵E是AB的中点,
∴EF是△ABD的中位线.
∴EF∥BD;
(2)解:∵∠ACB=60°,CA=CD,
∴△CAD是等边三角形,
∴∠ADC=60°,AD=DC=AC=8,
∴BD=BC﹣CD=12﹣8=4,
过点A作AM⊥BC,垂足为M,
∴AM=AD=×8=4,
S△ABD=BD AM=×4×4=8,
∵EF∥BD,
∴=,
∴=,
∴S△AEF=×8=2,
四边形BDFE的面积=S△ABD﹣S△AEF=8﹣2=6.
19.(1)证明:如图1中,
∵AE平分∠BAC,BE⊥AE于点E,
∴△ABD是等腰三角形,
∴BE=DE,
∵BF=FC,
∴EF=DC==(AC﹣AB).
(2)结论:EF=(AB﹣AC),
理由:如图2中,延长AC交BE的延长线于P.
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠APE,
∴AB=AP,
∵AE⊥BP,
∴E为BP的中点,
∴BE=PE,
∵点F为BC的中点,
∴BF=FC,
∴EF=PC=(AP﹣AC)=(AB﹣AC).
20.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC,∴GH∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
21.(1)解:∵点D、E分别是△ABC的边BC、AC边的中点,
∴DE为△ABC的中位线,
∴DE∥AB,DE=AB,
∵AB=10,
∴DE=5;
(2)证明:∵DE∥AB,FG∥AD,
∴四边形AFGD是平行四边形,
∴AF=DG.
22.(1)证明:如图1,∵DB=BC,点E是CD的中点,
∴BE⊥CD,
∴∠AEB=90°,
∵点F是AB的中点,
∴EF=AB.
(2)证明:如图2,∵AF=AB,EF=AB,
∴AF=EF,
∴∠EAB=∠FEA,
∵∠EAG=∠FEA,
∴∠EAB=∠EAG,
∵BE⊥CD,
∴∠AEB=∠AEG=90°,
在△ABE和△AGE中,
,
∴△ABE≌△AGE(ASA).
