高中数学人教A版(2019)必修第一册分层课时作业——5.7三角函数的应用(一般)(含解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册分层课时作业——5.7三角函数的应用(一般)(含解析) | 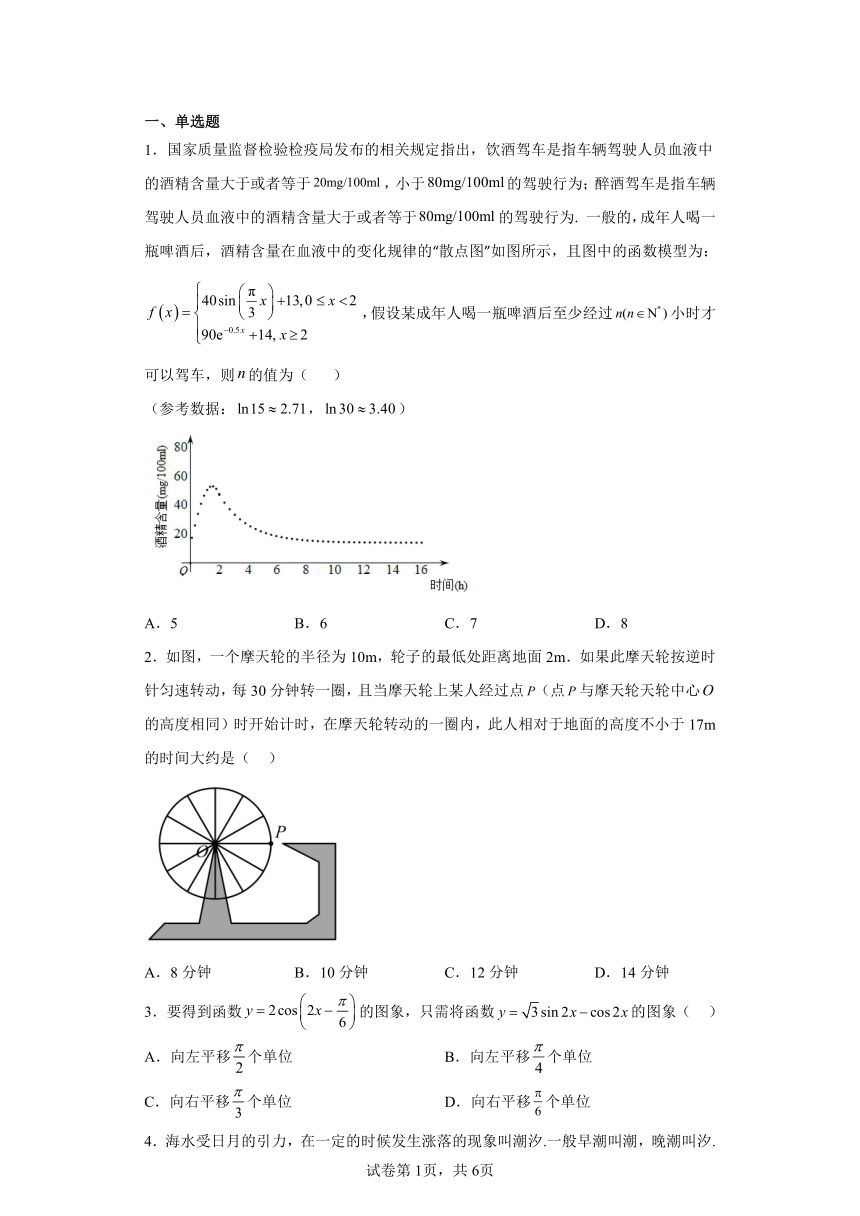 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 10:09:54 | ||
图片预览




文档简介
一、单选题
1.国家质量监督检验检疫局发布的相关规定指出,饮酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于,小于的驾驶行为;醉酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于的驾驶行为. 一般的,成年人喝一瓶啤酒后,酒精含量在血液中的变化规律的“散点图”如图所示,且图中的函数模型为: ,假设某成年人喝一瓶啤酒后至少经过小时才可以驾车,则的值为( )
(参考数据:,)
A.5 B.6 C.7 D.8
2.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
3.要得到函数的图象,只需将函数的图象( )
A.向左平移个单位 B.向左平移个单位
C.向右平移个单位 D.向右平移个单位
4.海水受日月的引力,在一定的时候发生涨落的现象叫潮汐.一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节每天的时间与水深值(单位:)记录表
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深值
已知港口的水的深度随时间变化符合函数,现有一条货船的吃水深度(船底与水面的距离)为,安全条例规定至少要有的安全间隙(船底与海底的距离),该船计划在中午点之后按规定驶入港口,并开始卸货,卸货时,其吃水深度以每小时的速度减小,小时卸完,则其在港口最多能停放( )A.小时 B.小时 C.小时 D.小时
5.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到应用.假定在水流稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.如图,将筒车抽象为一个几何图形(圆),筒车半径为4,筒车转轮的中心O到水面的距离为2,筒车每分钟沿逆时针方向转动4圈.规定:盛水筒M对应的点P从水中浮现(即P0时的位置)时开始计算时间,且以水轮的圆心O为坐标原点,过点O的水平直线为x轴建立平面直角坐标系.设盛水筒M从点P0运动到点P时所经过的时间为t(单位:),且此时点P距离水面的高度为h(单位:),则点P第一次到达最高点需要的时间为( ).
A.2 B.3 C.5 D.10
6.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置p(x,y).若初始位置为,当秒针从P0(注此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
A.y=sin B.y=sin
C.y=sin D.y=sin
二、多选题
7.将函数的图象向右平移个单位长度后,所得图象对应的函数为,则下列结论正确的是( )
A.函数的图象关于直线对称
B.函数的图象关于点对称
C.函数在上单调递减
D.函数在上恰有4个极值点
8.声音是由物体振动产生的声波.我们听到的每个音都是由纯音合成的,纯音的数学模型是函数.音有四要素:音调 响度 音长和音色.它们都与函数及其参数有关,比如:响度与振幅有关,振幅越大响度越大,振幅越小响度越小;音调与频率有关,频率低的声音低沉,频率高的声音尖锐;我们平时听到的乐音不只是一个音在响,而是许多音的结合,称为复合音.我们听到的声音对应的函数是结合上述材料及所学知识,下列说法错误的是( )
A.函数不具有奇偶性
B.函数在区间上单调递增
C.若某声音甲的对应函数近似为,则声音甲的响度一定比纯音响度小
D.若某声音乙的对应函数近似为,则声音乙一定比纯音更低沉
三、填空题
9.魏晋南北朝(公元220-581)时期,中国数学在测量学取得了长足进展.刘徽提出重差术,应用中国传统的出入相补原理,通过多次观测测量山高水深等数值,进而使中国的测量学达到登峰造极的地步,超越西方约一千年,关于重差术的注文在唐代成书,因其第题为测量海岛的高度和距离,故题为《海岛算经》.受此题启发,小明同学依照此法测量泾阳县崇文塔的高度(示意图如图所示),测得以下数据(单位:米):前表却行,表高,后表却行,表间.则塔高___________米.
10.在平面直角坐标系中,已知任意角以坐标原点为顶点,轴的非负半轴为始边,若终边经过点,且,定义:,称“”为“正余弦函数”,对于“正余弦函数”,有同学得到以下性质:
①该函数的值域为; ②该函数的图象关于原点对称;
③该函数的图象关于直线对称; ④该函数为周期函数,且最小正周期为;
⑤该函数的递增区间为.
其中正确的是__________.(填上所有正确性质的序号)
11.某时钟的秒针端点到中心点的距离为6cm,秒针均匀地绕点旋转,当时间时,点与钟面上标12的点重合,将,两点的距离表示成的函数,则_______,其中.
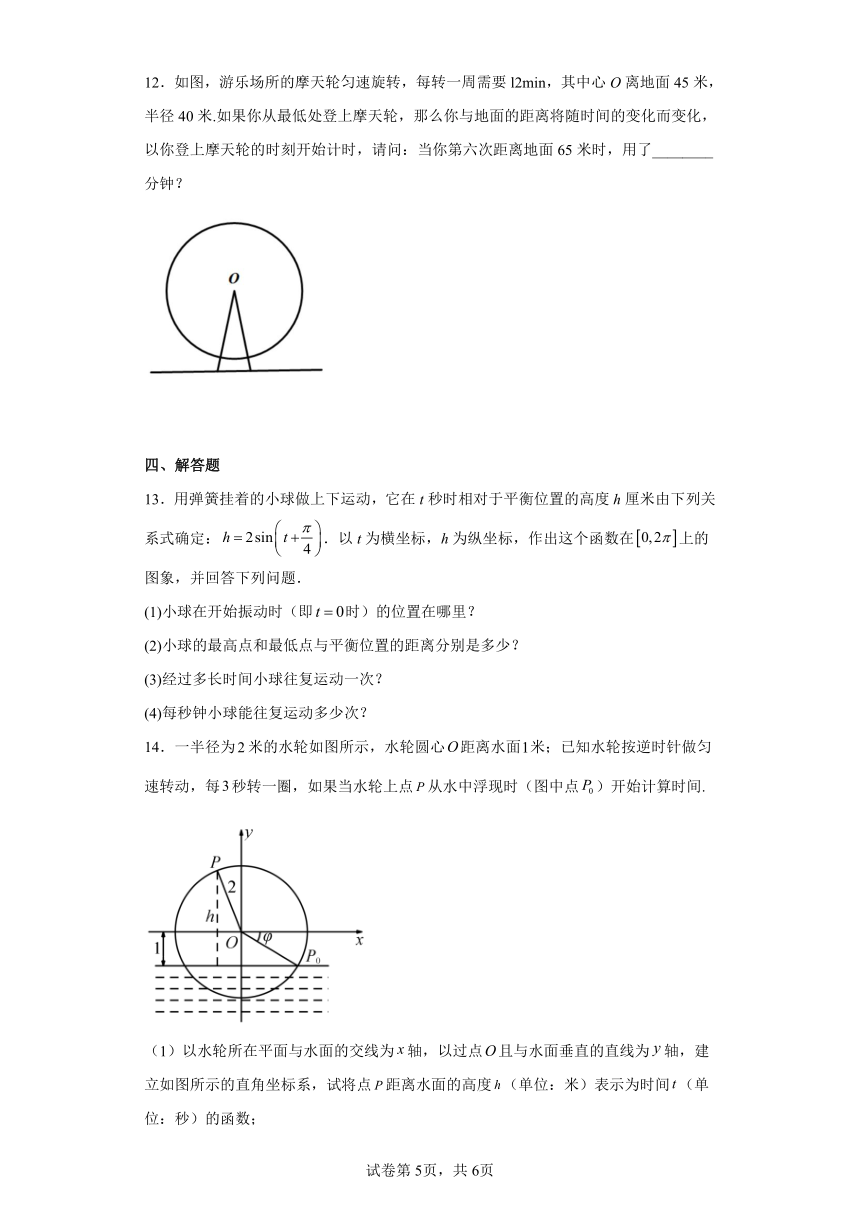
12.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?
四、解答题
13.用弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置的高度h厘米由下列关系式确定:.以t为横坐标,h为纵坐标,作出这个函数在上的图象,并回答下列问题.
(1)小球在开始振动时(即时)的位置在哪里?
(2)小球的最高点和最低点与平衡位置的距离分别是多少?
(3)经过多长时间小球往复运动一次?
(4)每秒钟小球能往复运动多少次?
14.一半径为米的水轮如图所示,水轮圆心距离水面米;已知水轮按逆时针做匀速转动,每秒转一圈,如果当水轮上点从水中浮现时(图中点)开始计算时间.
(1)以水轮所在平面与水面的交线为轴,以过点且与水面垂直的直线为轴,建立如图所示的直角坐标系,试将点距离水面的高度(单位:米)表示为时间(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点距水面的高度超过米?
15.已知函数,其图像过点.
(1)求φ的值;
(2)将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像,求函数在上的最大值和最小值.
16.如图,在直径为1的圆中,作一关于圆心对称、邻边互相垂直的十字形,其中.
(1)将十字形的面积表示成的函数;
(2)求十字形的最大面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】由散点图知,该人喝一瓶啤酒后个小时内酒精含量大于或者等于,所以,根据题意列不等式,解不等式结合即可求解.
【详解】由散点图知,该人喝一瓶啤酒后个小时内酒精含量大于或者等于,
所以所求,
由,即,
所以,即,
所以,
因为,所以最小为,
所以至少经过小时才可以驾车,
故选:B.
2.B
【解析】由题可得此人相对于地面的高度与时间的关系是,再令求出的范围即可得出.
【详解】设时间为时,此人相对于地面的高度为,
则由题可得当时,,
在时间时,此人转过的角为,
此时此人相对于地面的高度,
令,则,
所以,解得,
故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是.
故选:B.
【点睛】本题考查三角函数的实际应用,解题的关键是得出高度与时间的关系,再解三角函数不等式即可.
3.B
【分析】根据三角函数图象变换的知识确定正确选项.
【详解】,故只需向左平移个单位就可得到
.
故选:B
【点睛】本小题主要考查三角函数图象变换,考查辅助角公式、诱导公式,属于中档题.
4.B
【分析】由已知表格中数据求得,根据驶入港口大于等于6,离开时大于等于5,分析即可得答案.
【详解】由表格中的数据可知,,则.
由T=12,∴,故,
当x=3时,f(x)=7,则∴,即,得.
∴.
由,得,
即或
∴或.
又该船计划在中午12点之后按规定驶入港口,
∴k=1时,x=13,即该船应在13点入港并开始卸货,
卸货时,其吃水深度以每小时的速度减小,小时卸完,卸完后的吃水深度为,
所以该货船需要的安全水深为3+2=5米,由,得,
即或
∴或.
所以可以停留到18点,此时水深为5米,货船需要离港,则其在港口最多能停放5小时.
故选:B
5.C
【分析】设点离水面的高度为,根据题意求出,再令可求出结果.
【详解】设点离水面的高度为,
依题意可得,,,
所以,
令,得,得,,
得,,
因为点P第一次到达最高点,所以,
所以.
故选:C
6.C
【分析】先确定函数的周期,再假设函数的解析式,进而结合待定系数法可求函数的解析式,注意秒针是顺时针走动.
【详解】解:由题意,函数的周期为,
设函数解析式为(因为秒针是顺时针走动),
初始位置为,,
时,,
,
可取,
函数解析式为
故选:C.
7.AD
【分析】先根据图象变换得,再根据余弦函数性质研究对称性、单调性以及极值点,即可作出选择.
【详解】将函数的图象向右平移个单位长度后得
因为,所以函数的图象关于直线对称,即A正确;
因为,所以函数的图象不关于点对称,即B错误;
因为,所以函数单调递增,即C错误;
因为,所以当时函数取得极值,即函数在上恰有4个极值点,D正确;
故选:AD
【点睛】本题考查三角函数图象变换、余弦函数性质,考查基本分析求解能力,属中档题.
8.AC
【分析】对于A利用函数奇偶性的定义判断即可;
对于B利用增函数和增函数的和仍为增函数来判断;
对于C判断两个函数的振幅大小即可;
对于D求出两个函数的周期,进而得到频率大小,即可判断.
【详解】对于A,令,
则
则,且函数定义域为R,所以是奇函数,A错误;
对于B,因为
所以,,,都在上单调递增,
所以在上单调递增,B正确;
对于C,因为为奇函数,且,所以,
所以的振幅比的振幅大,所以C错误;
对于D,的最小正周期是
证明:若存在,使恒成立,则必有,
,
,因为,
,
又与不恒相等,故的最小正周期是,所以频率,
而的周期为,频率,所以D正确.
故选:AC.
9.87
【分析】可看出,,从而可得出,这样即可求出的值.
【详解】解:根据题意,,,
,解得(米,
(米.
故答案为:87
10.①④⑤.
【详解】分析:根据“正余弦函数”的定义得到函数,然后根据三角函数的图象与性质分别进行判断即可得到结论.
详解:①中,由三角函数的定义可知,
所以,所以是正确的;
②中,,所以,所以函数关于原点对称是错误的;
③中,当时,,所以图象关于对称是错误的;
④中,,所以函数为周期函数,且最小正周期为,所以是正确的;
⑤中,因为,令,
得,即函数的单调递增区间为,所以是正确的,
综上所述,正确命题的序号为①④⑤.
点睛:本题主要考查了函数的新定义的应用,以及三角函数的图象与性质的应用,其中解答中根据函数的新定义求出函数的表达式是解答的关键,同时要求熟练掌握三角函数的图象与性质是解答额基础,着重考查了分析问题和解答问题的能力,属于中档试题.
11.
【分析】设函数解析式为,由题意将、代入求出参数值,即可得解析式.
【详解】设,由题意知:,
当时,,则,,令得;
当时,,则,,令得,
所以.
故答案为:.
12.32.
【分析】根据题意得到,化简得到或,得到答案.
【详解】设时间为,,根据题意:,故.
故或,故或,.
故.
故答案为:.
【点睛】本题考查了三角函数的应用,意在考查学生的应用能力.
13.(1)小球在开始振动时在距离平衡位置厘米处
(2)都是2厘米
(3)秒
(4)
【分析】(1)作出函数图象,代入函数式计算可得;
(2)由图象可得最高点和最低点对应的值;
(3)由图象可得一个周期的时间;
(4)用1除以周期可得.
(1)
函数在上的图象如图.
当时,(厘米),即小球在开始振动时在距离平衡位置厘米处.
(2)
小球的最高点和最低点与平衡位置的距离都是2厘米.
(3)
小球往复运动一次就是一个周期,易知秒,即经过秒往复运动一次.
(4)
每秒钟往复运动的次数.
14.(1);(2)有时间点距水面的高度超过米.
【分析】(1)设,根据题意求得、的值,以及函数的最小正周期,可求得的值,根据的大小可得出的值,由此可得出关于的函数解析式;
(2)由得出,令,求得的取值范围,进而可解不等式,可得出的取值范围,进而得解.
【详解】(1)设水轮上圆心正右侧点为,轴与水面交点为,如图所示:
设,由,,可得,所以.
,,,
由题意可知,函数的最小正周期为,,
所以点距离水面的高度关于时间的函数为;
(2)由,得,
令,则,
由,解得,又,
所以在水轮转动的任意一圈内,有时间点距水面的高度超过米.
【点睛】本题考查三角函数模型的简单应用,根据题意建立函数解析式是解答的关键,考查计算能力,属于中等题.
15.(1)
(2)最大值和最小值分别为和
【分析】(1)代入已知点,由φ的范围可求得φ的值;
(2)由(1)得函数的解析式,再根据图象的平移和伸缩变换得出函数的解析式,由余弦函数的性质可求得其最值.
(1)
解:∵,且函数图像过点,
∴,即,解得,.
又,∴.
(2)
解: 由(1)知,将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像.
∵,∴,故.
∴在上的最大值和最小值分别为和.
16.(1);(2).
【分析】(1)设十字形面积为,易知,然后将代入求解.,
(2)由(1)的结论,利用二倍角的正弦和余弦公式,结合辅助角公式得到,再利用正弦函数的性质求解.
【详解】(1)设十字形面积为,
如图所示:
所以,
(2),
(设为锐角且),
当,即时,最大.
即当时,十字形取得最大面积,
.
【点睛】本题主要考查几何图形面积的求法以及数据恒等变换和三角函数性质的应用,还考查了数形结合的思想和运算求解的能力,属于中档题.
答案第1页,共2页
答案第1页,共2页
1.国家质量监督检验检疫局发布的相关规定指出,饮酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于,小于的驾驶行为;醉酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于的驾驶行为. 一般的,成年人喝一瓶啤酒后,酒精含量在血液中的变化规律的“散点图”如图所示,且图中的函数模型为: ,假设某成年人喝一瓶啤酒后至少经过小时才可以驾车,则的值为( )
(参考数据:,)
A.5 B.6 C.7 D.8
2.如图,一个摩天轮的半径为10m,轮子的最低处距离地面2m.如果此摩天轮按逆时针匀速转动,每30分钟转一圈,且当摩天轮上某人经过点(点与摩天轮天轮中心的高度相同)时开始计时,在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是( )
A.8分钟 B.10分钟 C.12分钟 D.14分钟
3.要得到函数的图象,只需将函数的图象( )
A.向左平移个单位 B.向左平移个单位
C.向右平移个单位 D.向右平移个单位
4.海水受日月的引力,在一定的时候发生涨落的现象叫潮汐.一般早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节每天的时间与水深值(单位:)记录表
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深值
已知港口的水的深度随时间变化符合函数,现有一条货船的吃水深度(船底与水面的距离)为,安全条例规定至少要有的安全间隙(船底与海底的距离),该船计划在中午点之后按规定驶入港口,并开始卸货,卸货时,其吃水深度以每小时的速度减小,小时卸完,则其在港口最多能停放( )A.小时 B.小时 C.小时 D.小时
5.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到应用.假定在水流稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.如图,将筒车抽象为一个几何图形(圆),筒车半径为4,筒车转轮的中心O到水面的距离为2,筒车每分钟沿逆时针方向转动4圈.规定:盛水筒M对应的点P从水中浮现(即P0时的位置)时开始计算时间,且以水轮的圆心O为坐标原点,过点O的水平直线为x轴建立平面直角坐标系.设盛水筒M从点P0运动到点P时所经过的时间为t(单位:),且此时点P距离水面的高度为h(单位:),则点P第一次到达最高点需要的时间为( ).
A.2 B.3 C.5 D.10
6.如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置p(x,y).若初始位置为,当秒针从P0(注此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
A.y=sin B.y=sin
C.y=sin D.y=sin
二、多选题
7.将函数的图象向右平移个单位长度后,所得图象对应的函数为,则下列结论正确的是( )
A.函数的图象关于直线对称
B.函数的图象关于点对称
C.函数在上单调递减
D.函数在上恰有4个极值点
8.声音是由物体振动产生的声波.我们听到的每个音都是由纯音合成的,纯音的数学模型是函数.音有四要素:音调 响度 音长和音色.它们都与函数及其参数有关,比如:响度与振幅有关,振幅越大响度越大,振幅越小响度越小;音调与频率有关,频率低的声音低沉,频率高的声音尖锐;我们平时听到的乐音不只是一个音在响,而是许多音的结合,称为复合音.我们听到的声音对应的函数是结合上述材料及所学知识,下列说法错误的是( )
A.函数不具有奇偶性
B.函数在区间上单调递增
C.若某声音甲的对应函数近似为,则声音甲的响度一定比纯音响度小
D.若某声音乙的对应函数近似为,则声音乙一定比纯音更低沉
三、填空题
9.魏晋南北朝(公元220-581)时期,中国数学在测量学取得了长足进展.刘徽提出重差术,应用中国传统的出入相补原理,通过多次观测测量山高水深等数值,进而使中国的测量学达到登峰造极的地步,超越西方约一千年,关于重差术的注文在唐代成书,因其第题为测量海岛的高度和距离,故题为《海岛算经》.受此题启发,小明同学依照此法测量泾阳县崇文塔的高度(示意图如图所示),测得以下数据(单位:米):前表却行,表高,后表却行,表间.则塔高___________米.
10.在平面直角坐标系中,已知任意角以坐标原点为顶点,轴的非负半轴为始边,若终边经过点,且,定义:,称“”为“正余弦函数”,对于“正余弦函数”,有同学得到以下性质:
①该函数的值域为; ②该函数的图象关于原点对称;
③该函数的图象关于直线对称; ④该函数为周期函数,且最小正周期为;
⑤该函数的递增区间为.
其中正确的是__________.(填上所有正确性质的序号)
11.某时钟的秒针端点到中心点的距离为6cm,秒针均匀地绕点旋转,当时间时,点与钟面上标12的点重合,将,两点的距离表示成的函数,则_______,其中.
12.如图,游乐场所的摩天轮匀速旋转,每转一周需要l2min,其中心O离地面45米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请问:当你第六次距离地面65米时,用了________分钟?
四、解答题
13.用弹簧挂着的小球做上下运动,它在t秒时相对于平衡位置的高度h厘米由下列关系式确定:.以t为横坐标,h为纵坐标,作出这个函数在上的图象,并回答下列问题.
(1)小球在开始振动时(即时)的位置在哪里?
(2)小球的最高点和最低点与平衡位置的距离分别是多少?
(3)经过多长时间小球往复运动一次?
(4)每秒钟小球能往复运动多少次?
14.一半径为米的水轮如图所示,水轮圆心距离水面米;已知水轮按逆时针做匀速转动,每秒转一圈,如果当水轮上点从水中浮现时(图中点)开始计算时间.
(1)以水轮所在平面与水面的交线为轴,以过点且与水面垂直的直线为轴,建立如图所示的直角坐标系,试将点距离水面的高度(单位:米)表示为时间(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点距水面的高度超过米?
15.已知函数,其图像过点.
(1)求φ的值;
(2)将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像,求函数在上的最大值和最小值.
16.如图,在直径为1的圆中,作一关于圆心对称、邻边互相垂直的十字形,其中.
(1)将十字形的面积表示成的函数;
(2)求十字形的最大面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】由散点图知,该人喝一瓶啤酒后个小时内酒精含量大于或者等于,所以,根据题意列不等式,解不等式结合即可求解.
【详解】由散点图知,该人喝一瓶啤酒后个小时内酒精含量大于或者等于,
所以所求,
由,即,
所以,即,
所以,
因为,所以最小为,
所以至少经过小时才可以驾车,
故选:B.
2.B
【解析】由题可得此人相对于地面的高度与时间的关系是,再令求出的范围即可得出.
【详解】设时间为时,此人相对于地面的高度为,
则由题可得当时,,
在时间时,此人转过的角为,
此时此人相对于地面的高度,
令,则,
所以,解得,
故在摩天轮转动的一圈内,此人相对于地面的高度不小于17m的时间大约是.
故选:B.
【点睛】本题考查三角函数的实际应用,解题的关键是得出高度与时间的关系,再解三角函数不等式即可.
3.B
【分析】根据三角函数图象变换的知识确定正确选项.
【详解】,故只需向左平移个单位就可得到
.
故选:B
【点睛】本小题主要考查三角函数图象变换,考查辅助角公式、诱导公式,属于中档题.
4.B
【分析】由已知表格中数据求得,根据驶入港口大于等于6,离开时大于等于5,分析即可得答案.
【详解】由表格中的数据可知,,则.
由T=12,∴,故,
当x=3时,f(x)=7,则∴,即,得.
∴.
由,得,
即或
∴或.
又该船计划在中午12点之后按规定驶入港口,
∴k=1时,x=13,即该船应在13点入港并开始卸货,
卸货时,其吃水深度以每小时的速度减小,小时卸完,卸完后的吃水深度为,
所以该货船需要的安全水深为3+2=5米,由,得,
即或
∴或.
所以可以停留到18点,此时水深为5米,货船需要离港,则其在港口最多能停放5小时.
故选:B
5.C
【分析】设点离水面的高度为,根据题意求出,再令可求出结果.
【详解】设点离水面的高度为,
依题意可得,,,
所以,
令,得,得,,
得,,
因为点P第一次到达最高点,所以,
所以.
故选:C
6.C
【分析】先确定函数的周期,再假设函数的解析式,进而结合待定系数法可求函数的解析式,注意秒针是顺时针走动.
【详解】解:由题意,函数的周期为,
设函数解析式为(因为秒针是顺时针走动),
初始位置为,,
时,,
,
可取,
函数解析式为
故选:C.
7.AD
【分析】先根据图象变换得,再根据余弦函数性质研究对称性、单调性以及极值点,即可作出选择.
【详解】将函数的图象向右平移个单位长度后得
因为,所以函数的图象关于直线对称,即A正确;
因为,所以函数的图象不关于点对称,即B错误;
因为,所以函数单调递增,即C错误;
因为,所以当时函数取得极值,即函数在上恰有4个极值点,D正确;
故选:AD
【点睛】本题考查三角函数图象变换、余弦函数性质,考查基本分析求解能力,属中档题.
8.AC
【分析】对于A利用函数奇偶性的定义判断即可;
对于B利用增函数和增函数的和仍为增函数来判断;
对于C判断两个函数的振幅大小即可;
对于D求出两个函数的周期,进而得到频率大小,即可判断.
【详解】对于A,令,
则
则,且函数定义域为R,所以是奇函数,A错误;
对于B,因为
所以,,,都在上单调递增,
所以在上单调递增,B正确;
对于C,因为为奇函数,且,所以,
所以的振幅比的振幅大,所以C错误;
对于D,的最小正周期是
证明:若存在,使恒成立,则必有,
,
,因为,
,
又与不恒相等,故的最小正周期是,所以频率,
而的周期为,频率,所以D正确.
故选:AC.
9.87
【分析】可看出,,从而可得出,这样即可求出的值.
【详解】解:根据题意,,,
,解得(米,
(米.
故答案为:87
10.①④⑤.
【详解】分析:根据“正余弦函数”的定义得到函数,然后根据三角函数的图象与性质分别进行判断即可得到结论.
详解:①中,由三角函数的定义可知,
所以,所以是正确的;
②中,,所以,所以函数关于原点对称是错误的;
③中,当时,,所以图象关于对称是错误的;
④中,,所以函数为周期函数,且最小正周期为,所以是正确的;
⑤中,因为,令,
得,即函数的单调递增区间为,所以是正确的,
综上所述,正确命题的序号为①④⑤.
点睛:本题主要考查了函数的新定义的应用,以及三角函数的图象与性质的应用,其中解答中根据函数的新定义求出函数的表达式是解答的关键,同时要求熟练掌握三角函数的图象与性质是解答额基础,着重考查了分析问题和解答问题的能力,属于中档试题.
11.
【分析】设函数解析式为,由题意将、代入求出参数值,即可得解析式.
【详解】设,由题意知:,
当时,,则,,令得;
当时,,则,,令得,
所以.
故答案为:.
12.32.
【分析】根据题意得到,化简得到或,得到答案.
【详解】设时间为,,根据题意:,故.
故或,故或,.
故.
故答案为:.
【点睛】本题考查了三角函数的应用,意在考查学生的应用能力.
13.(1)小球在开始振动时在距离平衡位置厘米处
(2)都是2厘米
(3)秒
(4)
【分析】(1)作出函数图象,代入函数式计算可得;
(2)由图象可得最高点和最低点对应的值;
(3)由图象可得一个周期的时间;
(4)用1除以周期可得.
(1)
函数在上的图象如图.
当时,(厘米),即小球在开始振动时在距离平衡位置厘米处.
(2)
小球的最高点和最低点与平衡位置的距离都是2厘米.
(3)
小球往复运动一次就是一个周期,易知秒,即经过秒往复运动一次.
(4)
每秒钟往复运动的次数.
14.(1);(2)有时间点距水面的高度超过米.
【分析】(1)设,根据题意求得、的值,以及函数的最小正周期,可求得的值,根据的大小可得出的值,由此可得出关于的函数解析式;
(2)由得出,令,求得的取值范围,进而可解不等式,可得出的取值范围,进而得解.
【详解】(1)设水轮上圆心正右侧点为,轴与水面交点为,如图所示:
设,由,,可得,所以.
,,,
由题意可知,函数的最小正周期为,,
所以点距离水面的高度关于时间的函数为;
(2)由,得,
令,则,
由,解得,又,
所以在水轮转动的任意一圈内,有时间点距水面的高度超过米.
【点睛】本题考查三角函数模型的简单应用,根据题意建立函数解析式是解答的关键,考查计算能力,属于中等题.
15.(1)
(2)最大值和最小值分别为和
【分析】(1)代入已知点,由φ的范围可求得φ的值;
(2)由(1)得函数的解析式,再根据图象的平移和伸缩变换得出函数的解析式,由余弦函数的性质可求得其最值.
(1)
解:∵,且函数图像过点,
∴,即,解得,.
又,∴.
(2)
解: 由(1)知,将函数的图像上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图像.
∵,∴,故.
∴在上的最大值和最小值分别为和.
16.(1);(2).
【分析】(1)设十字形面积为,易知,然后将代入求解.,
(2)由(1)的结论,利用二倍角的正弦和余弦公式,结合辅助角公式得到,再利用正弦函数的性质求解.
【详解】(1)设十字形面积为,
如图所示:
所以,
(2),
(设为锐角且),
当,即时,最大.
即当时,十字形取得最大面积,
.
【点睛】本题主要考查几何图形面积的求法以及数据恒等变换和三角函数性质的应用,还考查了数形结合的思想和运算求解的能力,属于中档题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
