高中数学人教A版(2019)必修第一册分层课时作业——5.7三角函数的应用(较难)(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册分层课时作业——5.7三角函数的应用(较难)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 09:58:44 | ||
图片预览



文档简介
一、单选题
1.如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为
A.5米 B.(4+)米
C.(4+)米 D.(4+)米
2.已知函数)的图象在区间上恰有个最低点,则的取值范围为( )
A. B. C. D.
3.如图,半圆的直径为,为直径的延长线上一点,且,为半圆上任意一点,以为边作等边三角形.当时,等于
A. B.
C. D.
4.如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小,若,则的最大值是( ).(仰角为直线与平面所成的角)
A. B. C. D.
5.如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图像是( )
A. B.
C. D.
6.已知一组函数则下列说法正确的个数是( )
①恒成立;②若为常数函数,则;
③在上单调递减,在上单调递增.
A.0 B.1 C.2 D.3
二、多选题
7.筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1),明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图2).
现有一个半径为3米的筒车按逆时针方向每分钟旋转1圈,筒车的轴心距离水面的高度为2米,设筒车上的某个盛水筒P到水面的距离为(单位:米)(在水面下则为负数),若以盛水筒P刚浮出水面为初始时刻,经过1秒后,下列命题正确的是( )(参考数据:)
A.,其中,且
B.,其中,且
C.当时,盛水筒再次进入水中
D.当时,盛水筒到达最高点
8.水车在古代是进行灌溉引水的工具,亦称“水转筒车”,是一种以水流作动力,取水灌田的工具.据史料记载,水车发明于隋而盛于唐,距今已有1000多年的历史是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为R的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.经过t秒后,水斗旋转到P点,设点P的坐标为,其纵坐标满足,则下列叙述正确的是( )
A.水斗作周期运动的初相为
B.在水斗开始旋转的60秒(含)中,其高度不断增加
C.在水斗开始旋转的60秒(含)中,其最高点离平衡位置的纵向距离是
D.当水斗旋转100秒时,其和初始点A的距离为6
三、填空题
9.在平面直角坐标系中,对任意角,设的终边上异于原点的任意一点的坐标为,它与原点的距离是.我们规定:比值分别叫做角的正割 余割 余切,分别记作,,,把分别叫做正割函数 余割函数 余切函数,则下列叙述正确的有___________(填上所有正确的序号)
①;
②;
③的定义域为;
④;
⑤.
10.如图,在平面四边形中,,,,则的取值范围是_____.
11.设,满足:,则的从小到大顺序为____.
12.已知南北回归线的纬度为,设地球表面某地正午太阳高度角为,为此时太阳直射纬度,为该地的纬度值,那么这三个量之间的关系是.当地夏半年取正值,冬半年取负值,如果在北半球某地(纬度为)的一幢高为的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离应不小于______(结果用含有和的式子表示).
四、解答题
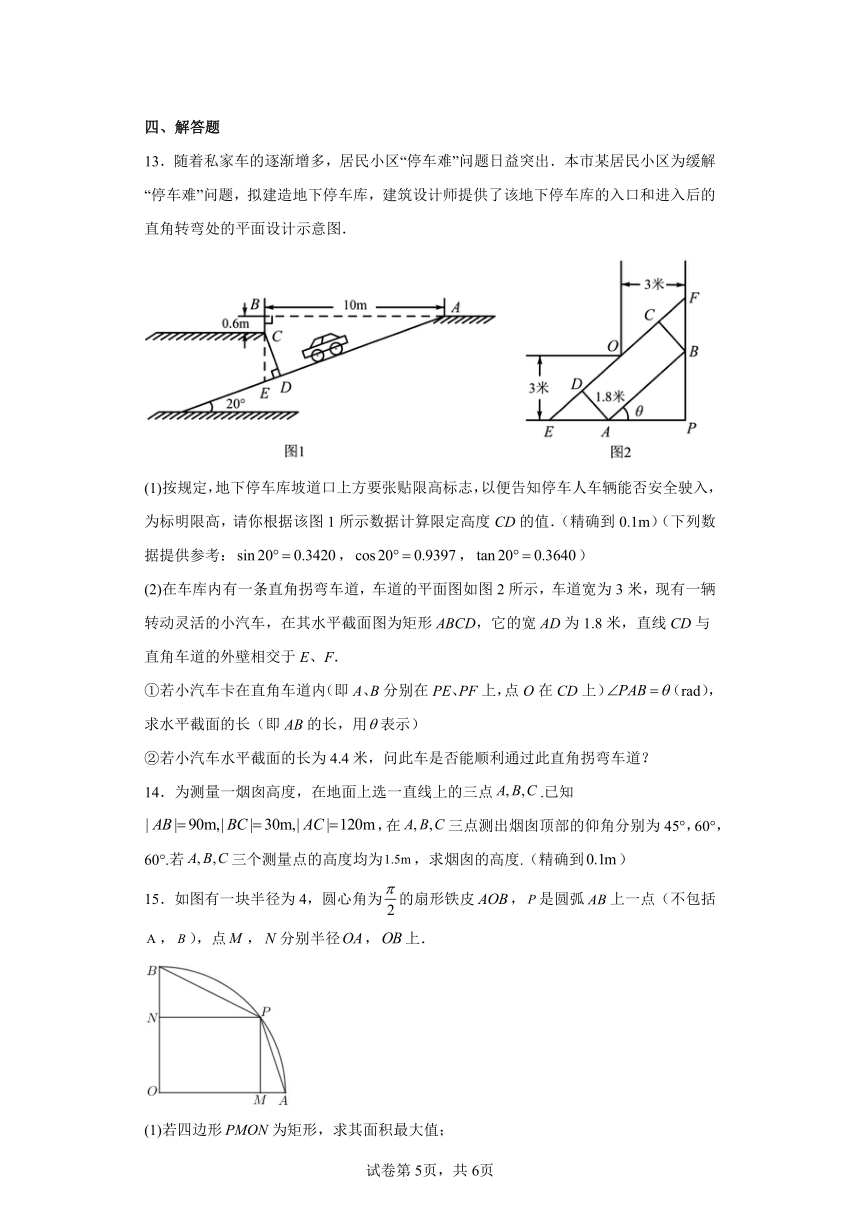
13.随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.
(1)按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图1所示数据计算限定高度CD的值.(精确到0.1m)(下列数据提供参考:,,)
(2)在车库内有一条直角拐弯车道,车道的平面图如图2所示,车道宽为3米,现有一辆转动灵活的小汽车,在其水平截面图为矩形ABCD,它的宽AD为1.8米,直线CD与直角车道的外壁相交于E、F.
①若小汽车卡在直角车道内(即A、B分别在PE、PF上,点O在CD上)(rad),求水平截面的长(即AB的长,用表示)
②若小汽车水平截面的长为4.4米,问此车是否能顺利通过此直角拐弯车道?
14.为测量一烟囱高度,在地面上选一直线上的三点.已知,在三点测出烟囱顶部的仰角分别为45°,60°,60°.若三个测量点的高度均为,求烟囱的高度.(精确到)
15.如图有一块半径为4,圆心角为的扇形铁皮,是圆弧上一点(不包括,),点,分别半径,上.
(1)若四边形为矩形,求其面积最大值;
(2)若和均为直角三角形,求它们面积之和的取值范围.
16.摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.
(1)游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差h(单位:m)关于t的函数解析式,并求高度差的最大值(精确到0.1).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】以圆心为原点,以水平方向为轴方向,以竖直方向为轴方向建立平面直角坐标系,则根据大风车的半径为,圆上最低点离地面1米,秒转动一圈,可得到与间的函数关系式,求出的坐标,即可求出点到点的距离与点的高度之和.
【详解】以圆心为原点,以水平方向为x轴方向,以竖直方向为y轴方向,
建立平面直角坐标系,如图所示.
设∠OP=θ,运动t(秒)后与地面的距离为f(t),又T=12,
∴θ=t,∴f(t)=3-2cos t,t≥0,
风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,
θ=6π+,P(,1),
∴点P的高度为3-2×=4.∵A(0,-3),∴AP==,
∴点P到点A的距离与点P的高度之和为(4+)米,故选D.
【点睛】本题主要考查三角函数的图象与性质的实际应用,意在考查转化思想以及数形结合思想的应用,属于中档题. 与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.
2.C
【分析】根据范围可得的范围;分别讨论在轴左侧无最低点、个最低点、个最低点和个最低点的情况,对应正弦函数的图象和性质可确定的范围.
【详解】
①在轴左侧无最低点,即当时,
当正好对应在上的第个最低点时,,
,(舍)
在轴左侧无最低点不合题意
②若在轴左侧仅有个最低点,即时,
,此时在轴左侧至少有个最低点
在轴左侧仅有个最低点不合题意
③若在轴左侧有个最低点,即时,
又,即
时,在恰有个最低点
④若在轴左侧有个最低点,即时,
,此时在轴左侧至多有个最低点
在轴左侧有个最低点不合题意
综上所述:
本题正确选项:
【点睛】本题考查根据正弦型函数的最值点个数求解参数范围的问题;关键是能够通过对最低点分布情况的分析,找到符合题意的分布情况,进而结合正弦函数图象得到不等关系,求得所求参数的范围,属于较难题.
3.B
【分析】四边形面积分为两个三角形计算,其中,利用余弦定理求AB,得正三角形ABC的面积,可得结果.
【详解】如图.
过点作于,则,即.
.
,
.
.
.
【点睛】本题考查三角函数的应用,函数式的建立,考查计算能力,属于中档题.
4.D
【分析】由题可得,,过作,交于,连接,则,设,分类讨论,若在线段上,则,可求出和,从而可得出,利用函数的单调性,可得出时,取得最大值;若在的延长线上,同理求出和,可得出,可得当时,函数取得最大值;结合两种情况的结果,即可得出结论.
【详解】解:,,
由勾股定理知,,
过点作交于,连结,则,
设,
若在线段上,则,
由,得,
在直角中,,
,
令,则函数在,单调递减,
时,取得最大值为;
若在的延长线上,,
在直角中,,
,
令,则可得时,函数取得最大值.
故答案为:.
5.A
【分析】设半径为,计算得到,,找出对应图像得到答案.
【详解】设半径为,则,
,故,
故选:
【点睛】本题考查了函数图像的识别,计算出函数表达式是解题的关键.
6.D
【详解】
所以N越大, 越小, ,当
取得最大值,所以正确;②是常函数时,对其赋值, 将其带入得
③
故本题正确答案为D.
7.BD
【分析】若为筒车的轴心的位置,为水面,为筒车经过秒后的位置,由题设知筒车的角速度,令易得,而、,即可求的解析式判断A、B的正误,、代入函数解析式求,即可判断C、D的正误.
【详解】
由题意知,如上图,若为筒车的轴心的位置,为水面,为筒车经过秒后的位置,筒车的角速度,令且,
∴,故,而,
∴,故A错误,B正确;
当时,,且,,
∴,故盛水筒没有进入水中,C错误;
当时,,且,即,
∴,故盛水筒到达最高点,D正确.
故选:BD
【点睛】关键点点睛:画出筒车与水面的简单平面示意图,利用及盛水筒P到水面的距离与相关线段的等量关系,写出函数解析式.
8.AD
【分析】求出圆的半径,利用周期求出,通过三角函数的解析式求出初相,再利用正弦函数的性质依次判断各选项即可.
【详解】对于A,由,知,,所以;
当时,点P在点A位置,有,解得,又,所以,故A正确;
对于B,可知,当,,所以函数先增后减,故B错误;
对于C,当,,,所以点到轴的距离的最大值为6,故C错误;
对于D,当时,,的纵坐标为,横坐标为,所以,故D正确.
故选:AD.
【点睛】方法点睛:求函数解析式的步骤:
(1)求A,B,确定函数的最大值M和最小值m,则,.
(2)求,确定函数的周期,则
(3)求,常用方法如下:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.
9.②④⑤
【分析】由题设新定义知:,,,由、、、以及正切二倍角公式,即可判断各项的正误.
【详解】
①,故错误;
②,故正确;
③,即,有,故错误;
④,故正确;
⑤,所以,故正确.
故答案为:②④⑤
【点睛】关键点点睛:新定义有,,,结合三角恒等变换判断各项的正误.
10.
【解析】如图,延长交于点,设,求出,即可求出的取值范围.
【详解】解:如图,延长交于点,则
在中,,
所以设,
因为,
所以,
所以,
所以,
因为,
所以的取值范围为,
故答案为:
【点睛】此题考查三角形中的几何计算,考查学生的计算能力,属于中档题.
11.
【详解】分析:由题意将原问题转化为函数图像的交点问题,数形结合整理计算即可求得最终结果.
详解:cosa=a表示曲线y=cosx与y=x的交点的横坐标即为a.
同理,曲线y=sin(cosx)与y=x的交点的横坐标即为b.
而曲线y=cos(sinx)与y=x的交点的横坐标即为c.
如图所示,在同一坐标系中作出曲线y=cosx,y=cos(sinx),y=sin(cosx)及直线y=x.
由于当时,有sinxcosx.
即当时,y=cos(sinx)的图象在y=cosx的上方.
由于时,.
在sinx即当时,y=sin(cosx)的图象在y=cosx的下方.
由此可知b点睛:本题主要考查三角函数的性质,数形结合的数学思想等知识,意在考查学生的转化能力和计算求解能力.
12.
【解析】根据题意,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线时的情况考虑,此时的太阳直射纬度为,依题意两楼的间距不小于MC,根据太阳高度角的定义,以及题设条件,解三角形,即得解.
【详解】如图:
设点A,B,C分别为太阳直射北回归线,赤道,南回归线时楼顶在地面上得投射点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线时的情况考虑,此时的太阳直射纬度为,依题意两楼的间距不小于MC,根据太阳高度角的定义得:
故答案为:
【点睛】本题考查了解三角形在实际问题中的应用,考查了学生综合分析,数学建模,数学运算的能力,属于较难题.
13.(1)2.8m;
(2)①,;②小汽车能够顺利通过直角转弯车道.
【分析】(1)根据给定条件,在两个直角三角形中,利用直角三角形边角关系计算作答.
(2)①利用给定图形结合直角三角形锐角三角函数定义,用表示EF,BE,CF即可作答;
②由①的结论,利用换元法并借助函数单调性,求出AB长的最小值作答.
(1)
图1中:在中,,,,又,
则(m),而m,有(m),
在中,,,,
则(m),
结合实际意义,四舍五入会使车辆卡住,可以使用去尾法,则m,
所以限定高度的值约为2.8m.
(2)
①图2中:依题意,则,,,,
又,设,
,;
②由①知,设,则,,,
则,
而,函数在上单调递增,则在上是减函数,
于是得当,即时,,
所以小汽车能够顺利通过直角转弯车道.
【点睛】思路点睛:涉及含有和的三角函数值域或最值问题,可以通过换元转化为整式函数或分式函数在某区间上的值域或最值问题解答.
14.
【分析】根据题意作出示意图,设烟囱高为x(1.5米以上的),C点到烟囱的水平距离为y,利用勾股定理及仰角的正切列出方程,即可求解.
【详解】如图,
设烟囱高为x(1.5米以上的),C点到烟囱的水平距离为y,A点仰角为,故A到烟囱的水平距离也为xB点与C点的仰角均为,B到烟囱的水平距离也为y,从烟囱根起来1.5米(记为点E),做BC的垂线,因为是等腰三角形,交BC于中点D.
在△AED中
,
即,
又,即,
代入(1)得:,
解得,
所以,
故烟囱高度为米.
【点睛】本题主要考查了实际问题中的解三角形问题,建立适当的数学模型是解决此类问题的关键,属于中档题.
15.(1)8;
(2).
【分析】(1)连接OP,令,用表示出矩形的面积,再借助三角函数计算作答.
(2)利用(1)中信息,用表示出和的面积和,再换元变形结合二次函数性质计算作答.
(1)
连接OP,如图,令,
因四边形为矩形,则,
于是得矩形的面积,而,
则当,即时,取最大值1,即有,
所以矩形面积最大值为8.
(2)
由(1)知,,则,,
和的面积和:
,
令,即,而,则,
,
则,显然在上单调递减,
当,即时,,而,因此,,
所以和的面积和的取值范围是:.
【点睛】思路点睛:涉及图形上的点变化引起的线段长度、图形面积等问题,若点的运动与某角的变化相关,可以设此角为自变量,借助三角函数解决.
16.(1),(2)游客甲在开始转动5min后距离地面的高度约为37.5m(3)甲、乙两人距离地面的高度差的最大值约为7.2m
【解析】(1)如图,设座舱距离地面最近的位置为点P,以轴心Q为原点,与地面平行的直线为x轴建立直角坐标系,座舱转动的角速度约为,计算得到答案.
(2)将数据代入解析式计算得到答案.
(3)计算,,相减得到
,计算最值得到答案.
【详解】(1)如图,设座舱距离地面最近的位置为点P,以轴心Q为原点,与地面平行的直线为x轴建立直角坐标系,
设时,游客甲位于点,以OP为终边的角为;
根据摩天轮转一周大约需要30min,可知座舱转动的角速度约为,
由题意可得,.
(2)当时,.
所以游客甲在开始转动5min后距离地面的高度约为37.5m.
(3)如图,甲、乙两人的位置分别用点A,B表示,则.
经过tmin后甲距离地面的高度为,
点B相对于点A始终落后,
此时乙距离地面的高度为.
则甲、乙距离地面的高度差,
利用,
可得,.
当,即(或228)时,h的最大值为.
所以甲、乙两人距离地面的高度差的最大值约为7.2m.
【点睛】本题考查了三角函数的应用,意在考查学生的应用能力和计算能力.
答案第1页,共2页
答案第1页,共2页
1.如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面1米,点O在地面上的射影为A.风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,则点P到点A的距离与点P的高度之和为
A.5米 B.(4+)米
C.(4+)米 D.(4+)米
2.已知函数)的图象在区间上恰有个最低点,则的取值范围为( )
A. B. C. D.
3.如图,半圆的直径为,为直径的延长线上一点,且,为半圆上任意一点,以为边作等边三角形.当时,等于
A. B.
C. D.
4.如图,某人在垂直于水平地面的墙面前的点处进行射击训练,已知点到墙面的距离为,某目标点沿墙面上的射线移动,此人为了准确瞄准目标点,需计算由点观察点的仰角的大小,若,则的最大值是( ).(仰角为直线与平面所成的角)
A. B. C. D.
5.如图,AB为定圆O的直径,点P为半圆AB上的动点.过点P作AB的垂线,垂足为Q,过Q作OP的垂线,垂足为M.记弧AP的长为x,线段QM的长为y,则函数y=f(x)的大致图像是( )
A. B.
C. D.
6.已知一组函数则下列说法正确的个数是( )
①恒成立;②若为常数函数,则;
③在上单调递减,在上单调递增.
A.0 B.1 C.2 D.3
二、多选题
7.筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1),明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(图2).
现有一个半径为3米的筒车按逆时针方向每分钟旋转1圈,筒车的轴心距离水面的高度为2米,设筒车上的某个盛水筒P到水面的距离为(单位:米)(在水面下则为负数),若以盛水筒P刚浮出水面为初始时刻,经过1秒后,下列命题正确的是( )(参考数据:)
A.,其中,且
B.,其中,且
C.当时,盛水筒再次进入水中
D.当时,盛水筒到达最高点
8.水车在古代是进行灌溉引水的工具,亦称“水转筒车”,是一种以水流作动力,取水灌田的工具.据史料记载,水车发明于隋而盛于唐,距今已有1000多年的历史是人类的一项古老的发明,也是人类利用自然和改造自然的象征,如图是一个半径为R的水车,一个水斗从点出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.经过t秒后,水斗旋转到P点,设点P的坐标为,其纵坐标满足,则下列叙述正确的是( )
A.水斗作周期运动的初相为
B.在水斗开始旋转的60秒(含)中,其高度不断增加
C.在水斗开始旋转的60秒(含)中,其最高点离平衡位置的纵向距离是
D.当水斗旋转100秒时,其和初始点A的距离为6
三、填空题
9.在平面直角坐标系中,对任意角,设的终边上异于原点的任意一点的坐标为,它与原点的距离是.我们规定:比值分别叫做角的正割 余割 余切,分别记作,,,把分别叫做正割函数 余割函数 余切函数,则下列叙述正确的有___________(填上所有正确的序号)
①;
②;
③的定义域为;
④;
⑤.
10.如图,在平面四边形中,,,,则的取值范围是_____.
11.设,满足:,则的从小到大顺序为____.
12.已知南北回归线的纬度为,设地球表面某地正午太阳高度角为,为此时太阳直射纬度,为该地的纬度值,那么这三个量之间的关系是.当地夏半年取正值,冬半年取负值,如果在北半球某地(纬度为)的一幢高为的楼房北面盖一新楼,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离应不小于______(结果用含有和的式子表示).
四、解答题
13.随着私家车的逐渐增多,居民小区“停车难”问题日益突出.本市某居民小区为缓解“停车难”问题,拟建造地下停车库,建筑设计师提供了该地下停车库的入口和进入后的直角转弯处的平面设计示意图.
(1)按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图1所示数据计算限定高度CD的值.(精确到0.1m)(下列数据提供参考:,,)
(2)在车库内有一条直角拐弯车道,车道的平面图如图2所示,车道宽为3米,现有一辆转动灵活的小汽车,在其水平截面图为矩形ABCD,它的宽AD为1.8米,直线CD与直角车道的外壁相交于E、F.
①若小汽车卡在直角车道内(即A、B分别在PE、PF上,点O在CD上)(rad),求水平截面的长(即AB的长,用表示)
②若小汽车水平截面的长为4.4米,问此车是否能顺利通过此直角拐弯车道?
14.为测量一烟囱高度,在地面上选一直线上的三点.已知,在三点测出烟囱顶部的仰角分别为45°,60°,60°.若三个测量点的高度均为,求烟囱的高度.(精确到)
15.如图有一块半径为4,圆心角为的扇形铁皮,是圆弧上一点(不包括,),点,分别半径,上.
(1)若四边形为矩形,求其面积最大值;
(2)若和均为直角三角形,求它们面积之和的取值范围.
16.摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.
(1)游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差h(单位:m)关于t的函数解析式,并求高度差的最大值(精确到0.1).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】以圆心为原点,以水平方向为轴方向,以竖直方向为轴方向建立平面直角坐标系,则根据大风车的半径为,圆上最低点离地面1米,秒转动一圈,可得到与间的函数关系式,求出的坐标,即可求出点到点的距离与点的高度之和.
【详解】以圆心为原点,以水平方向为x轴方向,以竖直方向为y轴方向,
建立平面直角坐标系,如图所示.
设∠OP=θ,运动t(秒)后与地面的距离为f(t),又T=12,
∴θ=t,∴f(t)=3-2cos t,t≥0,
风车圆周上一点M从最低点O开始,逆时针方向旋转40秒后到达P点,
θ=6π+,P(,1),
∴点P的高度为3-2×=4.∵A(0,-3),∴AP==,
∴点P到点A的距离与点P的高度之和为(4+)米,故选D.
【点睛】本题主要考查三角函数的图象与性质的实际应用,意在考查转化思想以及数形结合思想的应用,属于中档题. 与实际应用相结合的题型也是高考命题的动向,这类问题的特点是通过现实生活的事例考查书本知识,解决这类问题的关键是耐心读题、仔细理解题,只有吃透题意,才能将实际问题转化为数学模型进行解答.
2.C
【分析】根据范围可得的范围;分别讨论在轴左侧无最低点、个最低点、个最低点和个最低点的情况,对应正弦函数的图象和性质可确定的范围.
【详解】
①在轴左侧无最低点,即当时,
当正好对应在上的第个最低点时,,
,(舍)
在轴左侧无最低点不合题意
②若在轴左侧仅有个最低点,即时,
,此时在轴左侧至少有个最低点
在轴左侧仅有个最低点不合题意
③若在轴左侧有个最低点,即时,
又,即
时,在恰有个最低点
④若在轴左侧有个最低点,即时,
,此时在轴左侧至多有个最低点
在轴左侧有个最低点不合题意
综上所述:
本题正确选项:
【点睛】本题考查根据正弦型函数的最值点个数求解参数范围的问题;关键是能够通过对最低点分布情况的分析,找到符合题意的分布情况,进而结合正弦函数图象得到不等关系,求得所求参数的范围,属于较难题.
3.B
【分析】四边形面积分为两个三角形计算,其中,利用余弦定理求AB,得正三角形ABC的面积,可得结果.
【详解】如图.
过点作于,则,即.
.
,
.
.
.
【点睛】本题考查三角函数的应用,函数式的建立,考查计算能力,属于中档题.
4.D
【分析】由题可得,,过作,交于,连接,则,设,分类讨论,若在线段上,则,可求出和,从而可得出,利用函数的单调性,可得出时,取得最大值;若在的延长线上,同理求出和,可得出,可得当时,函数取得最大值;结合两种情况的结果,即可得出结论.
【详解】解:,,
由勾股定理知,,
过点作交于,连结,则,
设,
若在线段上,则,
由,得,
在直角中,,
,
令,则函数在,单调递减,
时,取得最大值为;
若在的延长线上,,
在直角中,,
,
令,则可得时,函数取得最大值.
故答案为:.
5.A
【分析】设半径为,计算得到,,找出对应图像得到答案.
【详解】设半径为,则,
,故,
故选:
【点睛】本题考查了函数图像的识别,计算出函数表达式是解题的关键.
6.D
【详解】
所以N越大, 越小, ,当
取得最大值,所以正确;②是常函数时,对其赋值, 将其带入得
③
故本题正确答案为D.
7.BD
【分析】若为筒车的轴心的位置,为水面,为筒车经过秒后的位置,由题设知筒车的角速度,令易得,而、,即可求的解析式判断A、B的正误,、代入函数解析式求,即可判断C、D的正误.
【详解】
由题意知,如上图,若为筒车的轴心的位置,为水面,为筒车经过秒后的位置,筒车的角速度,令且,
∴,故,而,
∴,故A错误,B正确;
当时,,且,,
∴,故盛水筒没有进入水中,C错误;
当时,,且,即,
∴,故盛水筒到达最高点,D正确.
故选:BD
【点睛】关键点点睛:画出筒车与水面的简单平面示意图,利用及盛水筒P到水面的距离与相关线段的等量关系,写出函数解析式.
8.AD
【分析】求出圆的半径,利用周期求出,通过三角函数的解析式求出初相,再利用正弦函数的性质依次判断各选项即可.
【详解】对于A,由,知,,所以;
当时,点P在点A位置,有,解得,又,所以,故A正确;
对于B,可知,当,,所以函数先增后减,故B错误;
对于C,当,,,所以点到轴的距离的最大值为6,故C错误;
对于D,当时,,的纵坐标为,横坐标为,所以,故D正确.
故选:AD.
【点睛】方法点睛:求函数解析式的步骤:
(1)求A,B,确定函数的最大值M和最小值m,则,.
(2)求,确定函数的周期,则
(3)求,常用方法如下:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.
9.②④⑤
【分析】由题设新定义知:,,,由、、、以及正切二倍角公式,即可判断各项的正误.
【详解】
①,故错误;
②,故正确;
③,即,有,故错误;
④,故正确;
⑤,所以,故正确.
故答案为:②④⑤
【点睛】关键点点睛:新定义有,,,结合三角恒等变换判断各项的正误.
10.
【解析】如图,延长交于点,设,求出,即可求出的取值范围.
【详解】解:如图,延长交于点,则
在中,,
所以设,
因为,
所以,
所以,
所以,
因为,
所以的取值范围为,
故答案为:
【点睛】此题考查三角形中的几何计算,考查学生的计算能力,属于中档题.
11.
【详解】分析:由题意将原问题转化为函数图像的交点问题,数形结合整理计算即可求得最终结果.
详解:cosa=a表示曲线y=cosx与y=x的交点的横坐标即为a.
同理,曲线y=sin(cosx)与y=x的交点的横坐标即为b.
而曲线y=cos(sinx)与y=x的交点的横坐标即为c.
如图所示,在同一坐标系中作出曲线y=cosx,y=cos(sinx),y=sin(cosx)及直线y=x.
由于当时,有sinx
即当时,y=cos(sinx)的图象在y=cosx的上方.
由于时,.
在sinx
由此可知b
12.
【解析】根据题意,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线时的情况考虑,此时的太阳直射纬度为,依题意两楼的间距不小于MC,根据太阳高度角的定义,以及题设条件,解三角形,即得解.
【详解】如图:
设点A,B,C分别为太阳直射北回归线,赤道,南回归线时楼顶在地面上得投射点,要使新楼一层正午的太阳全年不被前面的楼房遮挡,应取太阳直射南回归线时的情况考虑,此时的太阳直射纬度为,依题意两楼的间距不小于MC,根据太阳高度角的定义得:
故答案为:
【点睛】本题考查了解三角形在实际问题中的应用,考查了学生综合分析,数学建模,数学运算的能力,属于较难题.
13.(1)2.8m;
(2)①,;②小汽车能够顺利通过直角转弯车道.
【分析】(1)根据给定条件,在两个直角三角形中,利用直角三角形边角关系计算作答.
(2)①利用给定图形结合直角三角形锐角三角函数定义,用表示EF,BE,CF即可作答;
②由①的结论,利用换元法并借助函数单调性,求出AB长的最小值作答.
(1)
图1中:在中,,,,又,
则(m),而m,有(m),
在中,,,,
则(m),
结合实际意义,四舍五入会使车辆卡住,可以使用去尾法,则m,
所以限定高度的值约为2.8m.
(2)
①图2中:依题意,则,,,,
又,设,
,;
②由①知,设,则,,,
则,
而,函数在上单调递增,则在上是减函数,
于是得当,即时,,
所以小汽车能够顺利通过直角转弯车道.
【点睛】思路点睛:涉及含有和的三角函数值域或最值问题,可以通过换元转化为整式函数或分式函数在某区间上的值域或最值问题解答.
14.
【分析】根据题意作出示意图,设烟囱高为x(1.5米以上的),C点到烟囱的水平距离为y,利用勾股定理及仰角的正切列出方程,即可求解.
【详解】如图,
设烟囱高为x(1.5米以上的),C点到烟囱的水平距离为y,A点仰角为,故A到烟囱的水平距离也为xB点与C点的仰角均为,B到烟囱的水平距离也为y,从烟囱根起来1.5米(记为点E),做BC的垂线,因为是等腰三角形,交BC于中点D.
在△AED中
,
即,
又,即,
代入(1)得:,
解得,
所以,
故烟囱高度为米.
【点睛】本题主要考查了实际问题中的解三角形问题,建立适当的数学模型是解决此类问题的关键,属于中档题.
15.(1)8;
(2).
【分析】(1)连接OP,令,用表示出矩形的面积,再借助三角函数计算作答.
(2)利用(1)中信息,用表示出和的面积和,再换元变形结合二次函数性质计算作答.
(1)
连接OP,如图,令,
因四边形为矩形,则,
于是得矩形的面积,而,
则当,即时,取最大值1,即有,
所以矩形面积最大值为8.
(2)
由(1)知,,则,,
和的面积和:
,
令,即,而,则,
,
则,显然在上单调递减,
当,即时,,而,因此,,
所以和的面积和的取值范围是:.
【点睛】思路点睛:涉及图形上的点变化引起的线段长度、图形面积等问题,若点的运动与某角的变化相关,可以设此角为自变量,借助三角函数解决.
16.(1),(2)游客甲在开始转动5min后距离地面的高度约为37.5m(3)甲、乙两人距离地面的高度差的最大值约为7.2m
【解析】(1)如图,设座舱距离地面最近的位置为点P,以轴心Q为原点,与地面平行的直线为x轴建立直角坐标系,座舱转动的角速度约为,计算得到答案.
(2)将数据代入解析式计算得到答案.
(3)计算,,相减得到
,计算最值得到答案.
【详解】(1)如图,设座舱距离地面最近的位置为点P,以轴心Q为原点,与地面平行的直线为x轴建立直角坐标系,
设时,游客甲位于点,以OP为终边的角为;
根据摩天轮转一周大约需要30min,可知座舱转动的角速度约为,
由题意可得,.
(2)当时,.
所以游客甲在开始转动5min后距离地面的高度约为37.5m.
(3)如图,甲、乙两人的位置分别用点A,B表示,则.
经过tmin后甲距离地面的高度为,
点B相对于点A始终落后,
此时乙距离地面的高度为.
则甲、乙距离地面的高度差,
利用,
可得,.
当,即(或228)时,h的最大值为.
所以甲、乙两人距离地面的高度差的最大值约为7.2m.
【点睛】本题考查了三角函数的应用,意在考查学生的应用能力和计算能力.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
