2021-2022学年青岛版七年级数学下册9.3平行线的性质 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年青岛版七年级数学下册9.3平行线的性质 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 07:02:34 | ||
图片预览




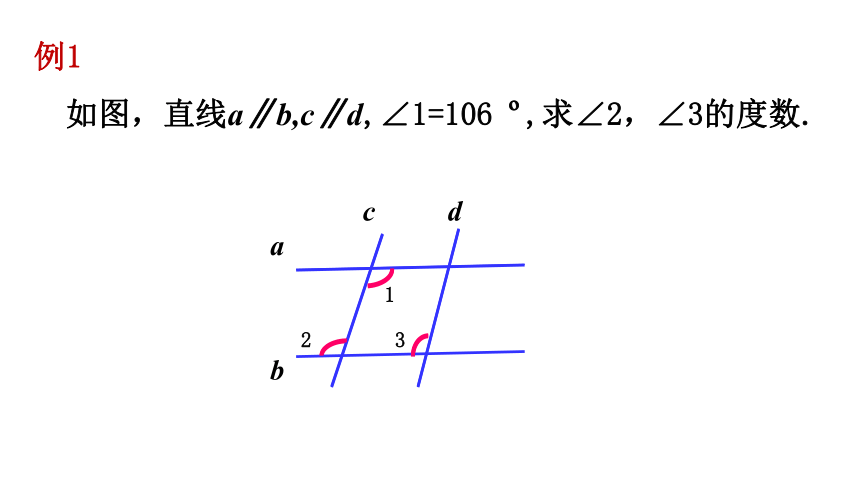
文档简介
(共16张PPT)
9.3 平行线的性质
找出下列图形中的同位角,内错角,同旁内角
∠1和∠5, ∠2和∠6,
∠3和∠7, ∠4和∠8
∠2和∠8, ∠3和∠5
∠2和∠5, ∠3和∠8
同位角:
内错角:
同旁内角:
1
课堂导入-复习回顾
世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成塔高54.5米.
1
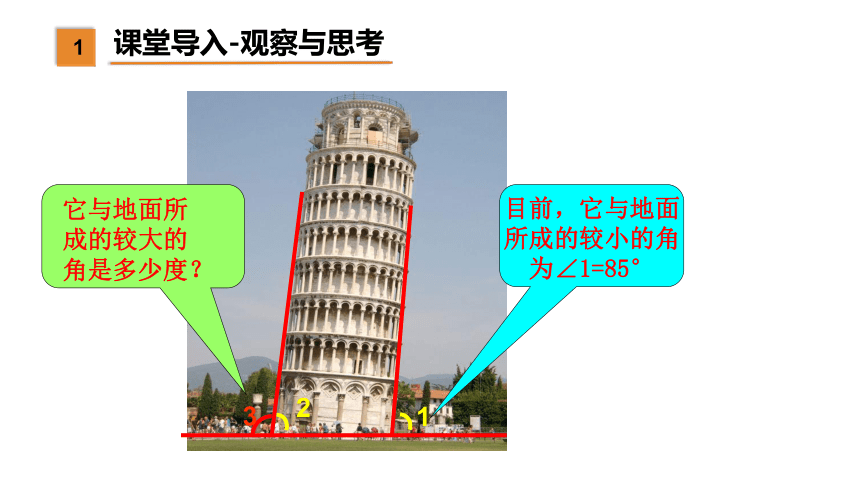
课堂导入-创设情境
目前,它与地面所成的较小的角
为∠1=85°
2
3
它与地面所
成的较大的
角是多少度?
1
课堂导入-观察与思考
1
1、通过实际操作和说理,掌握平行线的三条性质;
2、在具体问题中,会恰当运用平行线的性质进行说理,解决与“三线八角”有关的计算问题;
3、了解平行线之间距离的意义,能度量两条平行线之间的距离.
学习目标
如图,直线a∥b,c∥d,∠1=106 ,求∠2,∠3的度数.
c d
a
1
2 3
b
例1
C
D
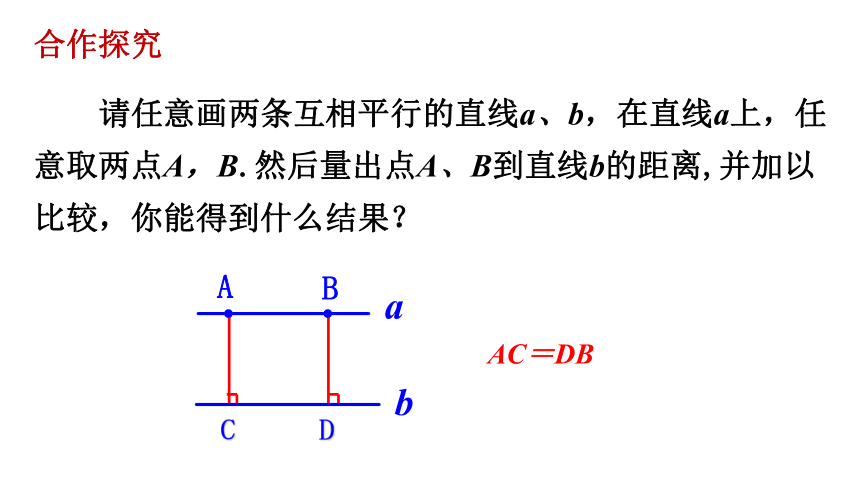
请任意画两条互相平行的直线a、b,在直线a上,任意取两点A,B.然后量出点A、B到直线b的距离,并加以比较,你能得到什么结果?
AC=DB
合作探究
C
D
两条平行线中,一条直线上的点到另一条直线的距离处处相等.
这个距离就叫做这两条平行线之间的距离.
注意是垂线段的长度,而不是垂线段
如图,已知平行线AB,CD被直线AE所截.
2
4
3
1
A
B
C
D
E
如图梯子的各条横档互相平行∠1=100 °,求∠2 的度数.
1
2
3
A
B
C
D
2.如图(1),若AD∥BC,则
∠______=∠_______,∠_______=∠_______,
∠ABC+∠_______=180°;
(2)若DC∥AB,则 ∠______=∠_______,
∠_______=∠_____, ∠ABC+∠_______ =180°.
A
B
C
D
1
5
4
8
BAD
2
6
3
7
BCD
如图是梯形有上底的部分,已量得∠A=115°,∠D=100°.求:梯形另外两个角各是多少度?
D
今天收获了什么?
1. 判断题:
(1)两条直线被第三条直线所截,同旁内角互补( )
(2)两条平行线被第三条直线所截,同位角相等 ( )
2.选择题:
(1)如图:DE是过点A的直线,如果DE∥BC,那么 ( )
A ∠3=∠2
B ∠C=∠2
C ∠C=∠1
D ∠C=∠B
×
√
C
达标检测
4.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通,则乙地所修公路的走向是_______,因为_________.
3.∠1和∠2是直线AB,CD被直线EF
所截而成的内错角,那么∠1和∠2 的大
小关系是( )
A.∠1=∠2 B.∠1>∠2;
C.∠1<∠2 D.无法确定
D
北偏东56°
两直线平行内错角相等
5.将证明过程的理由填在括号内:
已知:如图AB∥CD,直线EF交 AB 于点E,
交CD于点F .
求证:∠1+∠3=180°.
证明:∵ AB∥CD ( )
∴ ∠1=∠2 ( )
∵ ∠2+∠3=180° ( )
∴ ∠1+∠3=180° ( )
已知
两直线平行内错角相等
邻补角
等量代换
9.3 平行线的性质
找出下列图形中的同位角,内错角,同旁内角
∠1和∠5, ∠2和∠6,
∠3和∠7, ∠4和∠8
∠2和∠8, ∠3和∠5
∠2和∠5, ∠3和∠8
同位角:
内错角:
同旁内角:
1
课堂导入-复习回顾
世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成塔高54.5米.
1
课堂导入-创设情境
目前,它与地面所成的较小的角
为∠1=85°
2
3
它与地面所
成的较大的
角是多少度?
1
课堂导入-观察与思考
1
1、通过实际操作和说理,掌握平行线的三条性质;
2、在具体问题中,会恰当运用平行线的性质进行说理,解决与“三线八角”有关的计算问题;
3、了解平行线之间距离的意义,能度量两条平行线之间的距离.
学习目标
如图,直线a∥b,c∥d,∠1=106 ,求∠2,∠3的度数.
c d
a
1
2 3
b
例1
C
D
请任意画两条互相平行的直线a、b,在直线a上,任意取两点A,B.然后量出点A、B到直线b的距离,并加以比较,你能得到什么结果?
AC=DB
合作探究
C
D
两条平行线中,一条直线上的点到另一条直线的距离处处相等.
这个距离就叫做这两条平行线之间的距离.
注意是垂线段的长度,而不是垂线段
如图,已知平行线AB,CD被直线AE所截.
2
4
3
1
A
B
C
D
E
如图梯子的各条横档互相平行∠1=100 °,求∠2 的度数.
1
2
3
A
B
C
D
2.如图(1),若AD∥BC,则
∠______=∠_______,∠_______=∠_______,
∠ABC+∠_______=180°;
(2)若DC∥AB,则 ∠______=∠_______,
∠_______=∠_____, ∠ABC+∠_______ =180°.
A
B
C
D
1
5
4
8
BAD
2
6
3
7
BCD
如图是梯形有上底的部分,已量得∠A=115°,∠D=100°.求:梯形另外两个角各是多少度?
D
今天收获了什么?
1. 判断题:
(1)两条直线被第三条直线所截,同旁内角互补( )
(2)两条平行线被第三条直线所截,同位角相等 ( )
2.选择题:
(1)如图:DE是过点A的直线,如果DE∥BC,那么 ( )
A ∠3=∠2
B ∠C=∠2
C ∠C=∠1
D ∠C=∠B
×
√
C
达标检测
4.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通,则乙地所修公路的走向是_______,因为_________.
3.∠1和∠2是直线AB,CD被直线EF
所截而成的内错角,那么∠1和∠2 的大
小关系是( )
A.∠1=∠2 B.∠1>∠2;
C.∠1<∠2 D.无法确定
D
北偏东56°
两直线平行内错角相等
5.将证明过程的理由填在括号内:
已知:如图AB∥CD,直线EF交 AB 于点E,
交CD于点F .
求证:∠1+∠3=180°.
证明:∵ AB∥CD ( )
∴ ∠1=∠2 ( )
∵ ∠2+∠3=180° ( )
∴ ∠1+∠3=180° ( )
已知
两直线平行内错角相等
邻补角
等量代换
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
