六年级下册数学人教版 平面图形的认识与测量(概念、特征) 课件 (共53张PPT)
文档属性
| 名称 | 六年级下册数学人教版 平面图形的认识与测量(概念、特征) 课件 (共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览



文档简介
(共53张PPT)
平面图形的
认识与测量
(概念、特征)
点
线
面
体
几何图形的前世今生:
点动成线
线动成面
面动成体
一、引入复习
我们学过哪些平面图形和立体图形?你能对学过的图形进行分类吗?
问题
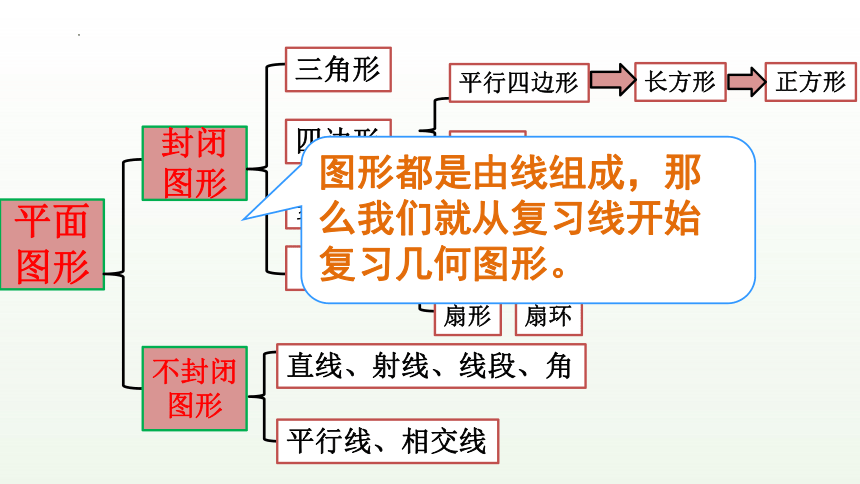
平面图形
封闭图形
不封闭图形
三角形
四边形
多边形
圆
平行四边形
直线、射线、线段、角
扇形
圆环
圆形
长方形
正方形
梯形
平行线、相交线
半圆形
扇环
图形都是由线组成,那么我们就从复习线开始复习几何图形。
二、整理复习
1.复习直线、射线、线段
(1)画一画
请同学们在纸上分别画出一条直线、射线、线段。
●
●
●
直线
射线
线段
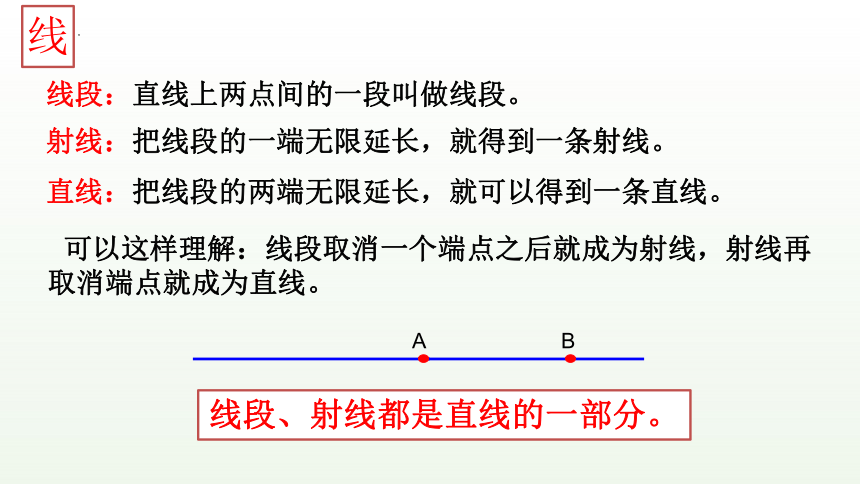
线
线段:直线上两点间的一段叫做线段。
射线:把线段的一端无限延长,就得到一条射线。
直线:把线段的两端无限延长,就可以得到一条直线。
可以这样理解:线段取消一个端点之后就成为射线,射线再取消端点就成为直线。
A
B
线段、射线都是直线的一部分。
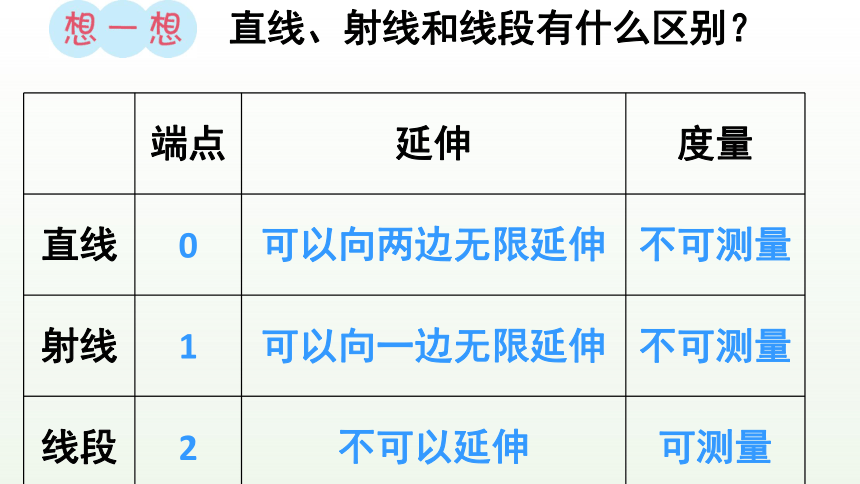
直线、射线和线段有什么区别?
端点 延伸 度量
直线 0 可以向两边无限延伸 不可测量
射线 1 可以向一边无限延伸 不可测量
线段 2 不可以延伸 可测量
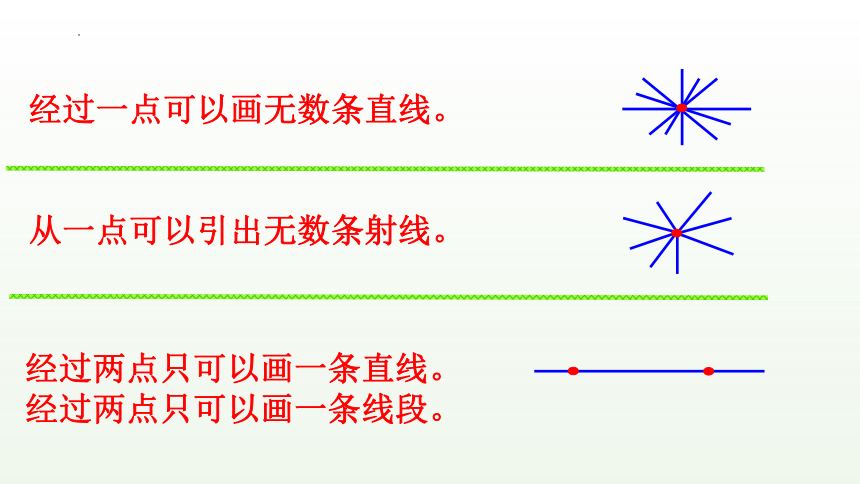
经过一点可以画无数条直线。
从一点可以引出无数条射线。
经过两点只可以画一条直线。
经过两点只可以画一条线段。
关于距离:
两点之间的距离,线段最短。
直线外一点到这条直线的距离,垂直线段最短。
两条平行线之间的距离,垂直线段最短。
A
B
A
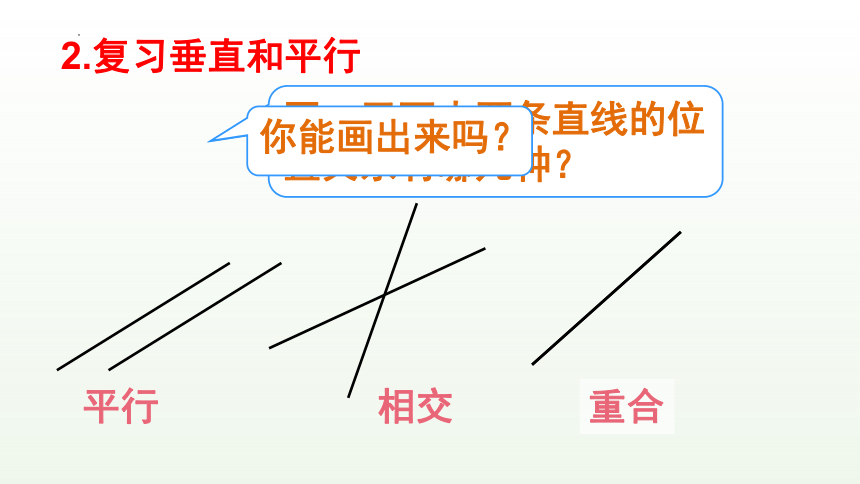
2.复习垂直和平行
同一平面内两条直线的位置关系有哪几种?
你能画出来吗?
平行
相交
重合
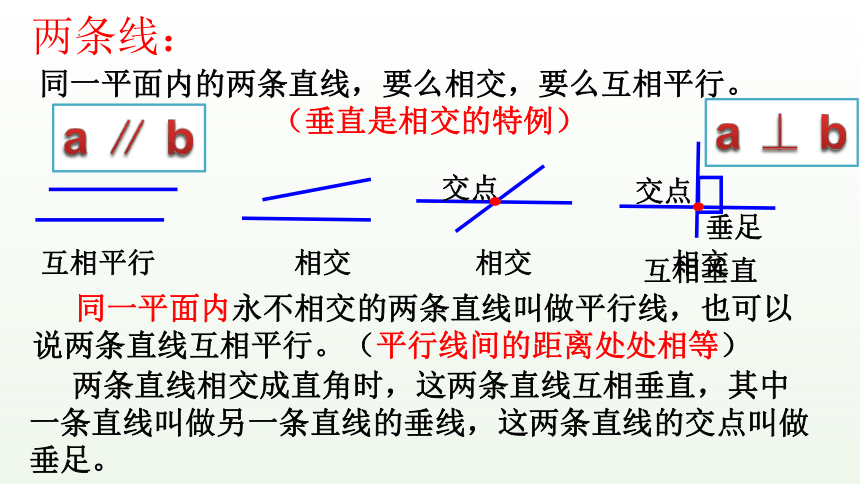
两条线:
同一平面内的两条直线,要么相交,要么互相平行。
(垂直是相交的特例)
同一平面内永不相交的两条直线叫做平行线,也可以说两条直线互相平行。(平行线间的距离处处相等)
相交
相交
互相平行
交点
两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
相交
交点
互相垂直
垂足
a ∥ b
a ⊥ b
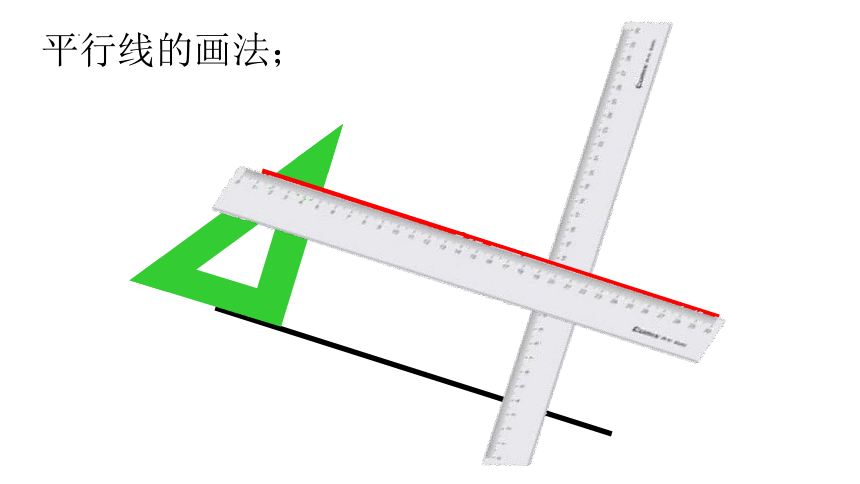
平行线的画法;
A
l
O
l1
l2
思考
你能分别量出点O到直线l的距离、平行线l1与l2之间的距离吗?
从O点向直线l可以作无数条线段,在这些线段中,垂直线段最短。
用放大镜看角,角的边变长,大小没变
3.复习角
(1)角的定义:
从一个点引出的两条射线组成的图形叫做角
这个点叫做角的顶点,这两条射线叫做角的边
O
角通常用符号“∠”来表示。
边
顶点
边
比较下面∠1和∠2的大小,并说说角的大小与什么有关。
∠2>∠1,角的大小与两边张开的程度有关,与边的长短无关。
问题
角的两条边叉开得越大,角越大;叉开得越小,角就越小。角的大小与两条边的长短无关。
(2)角的分类:
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
外刻度线
内刻度线
0刻度线
中心点
测量角的大小的工具是量角器。
把半圆分成180等份,每一份所对的角叫做 。
一度角
记作 “ 1°” 。
1°
量角的方法:
①把量角器放在角的上面,使量角器的中心与角的顶点重合。
②调整量角器,使“0”刻度线与角的一条边重合。
③读出角的另一边所对量角器上的度数,就是这个角的度数。
121°
121°
画角的方法:
①确定顶点,画一条射线;
②使量角器的中心与射线的端点重合,“0”刻度线与射线重合;
③在量角器上找出要画的角的度数的刻度,点上一个点;
④把射线的端点与刚才的点连起来。
60°
4.复习三角形
三角形的各部分名称:围成三角形的三条边叫做三角形的边;每两条边的交点叫做三角形的顶点;每两条边所形成的角叫做三角形的内角。(任意一个三角形都有3条边、3个顶点、3个角)
三角形的高:从三角形的一个顶点向它的对边作一条垂线,顶点与垂足之间的线段叫做三角形的高。任意一个三角形都有三条高;三角形的高和底是相互对应的。
等腰三角形
腰
腰
底
顶角
底角
底角
腰
顶角
腰
底角
底角
底
等腰直角三角形
腰
腰
底
顶角
底角
底角
等腰三角形
等腰三角形
有两条边相等的三角形叫做等腰三角形。其中相等的两条边叫做腰,另一条叫做底。两条腰的夹角叫做顶角,腰和底的夹角叫做底角,等腰三角形的两个底角度数相等。
边
边
边
等边三角形
(又叫正三角形)
三条边都相等的三角形叫做等边三角形,又叫正三角形。等边三角形的三条边长度相等,三个角的大小相等,都是60°。等边三角形是特殊的等腰三角形。
(1)三角形的分类
按边分
按角分
不等边三角形(三边都不相等)
(不是轴对称图形)
等腰
三角形
钝角三角形(有一个角是钝角)
锐角三角形(三个角都是锐角)
等边三角形或正三角形
(有三条边相等)(三个内角相等都是600)有3条对称轴
等腰三角形(有两条边相等)
(两个底角相等)有2条对称轴
直角三角形(有一个角是直角)
三角形
等边三角形一定是等腰三角形;
等腰三角形不一定是等边三角形。
有一个角是600 的等腰三角形
一定是等边三角形
一个三角形中最多有1个直角、1个
钝角;至少有2个锐角。
(2)三角形的特征
你知道三角形的特征有哪些?
1
具有稳定性(不易变形)
2
内角和180°
3
三角形的任意两边之和大于第三边
(任意两边之差小于第三边)
在直角三角形中,斜边永远大于任意一条直角边。
四边形的意义:在同一平面内,由四条线段首尾顺次相接围成的封闭图形叫做四边形。
四边形具有不稳定性(容易变形);四边形的四个内角和是360°。
5.复习四边形
长方形
两组对边分别平行并且相等,四个角都是直角的四边形叫做长方形。
长方形中较长的一组对边叫做长方形的长,较短的一组对边叫做长方形的宽。
长方形是特殊的平行四边形。
长
宽
长方形
长方形
长
宽
正方形
四条边相等,四个角都是直角的四边形叫做正方形。
正方形是特殊的长方形。
正方形
边长
平行四边形
两组对边分别平行的四边形叫做平行四边形。平行四边形对边的长度相等,对角的大小也相等。
从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,这条边叫做平行四边形的底。
底
高
平行四边形
高
底
梯 形
只有一组对边平行的四边形叫做梯形。
在梯形里,互相平行的一组对边叫做梯形的上底和下底,不平行的一组叫做梯形的腰,上底和下底之间的距离叫做梯形的高。
两腰相等的梯形叫做等腰梯形;有一个直角的梯形叫做直角梯形。
上底
下底
腰
腰
高
普通梯形
等腰梯形
直角梯形
四边形的分类
四边形
两组对边互不平行
只有一组对边平行
不规则四边形
梯形
两组对边分别平行
平行四边形
四个角
都是直角
长方形
四条边
都相等
正方形
四条边
都相等
菱形
四个角
都是直角
两腰相等
等腰梯形
有一个角是直角
直角梯形
也可以用下图分类:
四边形
不规则四边形
梯形
平行四边形
长方形
正方形
菱形
等腰梯形
直角梯形
还可以这样分类:
要画出一个圆,需要先确定什么?
圆心
半径
动手试试,任意画一个圆吧。
O
r
6.复习圆、圆环、扇形
圆心决定圆的位置,半径(直径)决定圆的大小。
问题
关于圆你都知道哪些知识呢?
一个圆有无数条半径,一般用字母r表示;有无数条直径,一般用字母d表示。
同一个圆内,直径的长度是半径的2倍,
即:d=2r。(直径是圆里最长的线段)
圆即是一种封闭的曲线图形;也是轴对称图形,它有无数条对称轴。
一
二
三
用圆规画圆时,针尖所在的点叫做圆心,一般用字母O表示。
连接圆心和圆上任意一点的线段
叫做半径,一般用字母r表示。
通过圆心并且两端都在圆上的线
段叫做直径,一般用字母d表示。
半径的长度就是圆规两个脚之间的距离。
圆的画法:
1、把圆规的两脚分开,定好两脚间
的距离(即半径)。
2、把有针尖的一只脚固定在一点(即
圆心上)。
3、把装有铅笔尖的一只脚旋转一周,
就画出一个圆。
定半径
定圆心
旋转一周
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
圆环有什么特点?
1、同心圆。
2、两圆间的距离处处相等。
3、是轴对称图形,有无数条对称轴。
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
◇ 复习扇形和扇形的各部分名称
1.一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。扇形是圆的一部分。
2.在同一个圆中,圆心角越大,扇形越大;在不同的圆中,圆心角相同的扇形,半径越大,扇形越大。
3.扇形的大小与圆心角和半径都有关。
巩固练习
1、 圆中心的一点叫做( ),一般用字母( )表示。
2、 连接圆心和圆上任意一点的线段叫做( ),一般用字母r表示。
3、通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
4、一个圆内有( )条直径,( )条半径。并且( )条直径等于2 条半径。
5、圆是( )图形,有( )条对称轴。
圆心
O
半径
直径
无数
无数
1
轴对称
无数
填空:
6、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。
7、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
8、圆中最长的线段是圆的( )。
9、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是( )、( )、( )。
不变
增加
直径
曲线
圆心
60cm
120cm
180cm
填空:
填空:
10、三角形的一个内角正好等于其余两个内角的和,这是一个( )三角形。
11、一个等腰三角形,它的顶角是72 ,它的底角是( )度。12、6时整,时针与分针组成的角的度数是( )
13、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是( )厘米,最少是( )厘米。
24、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是( )厘米。
直角
54
1800
21
18
2
1、大于90°的角叫钝角。( )
2、角的两条边越长,角就越大。( )
3、钟表的分针旋转一周,时针旋转30°。( )
4、可以画一条长10厘米的直线。( )
5、平角就是一条直线。( )
×
×
√
×
×
判 断
6、两条直线不相交就平行。( )
7、直线的两端可以无限延长。( )
8、一个20°的角用2倍放大镜看,会看到一个40°的
角。( )
9、一个平角减去一个锐角,得到一个钝角。( )
10、射线比直线短。( )
11、两条直线的位置关系可分为三种:垂直、平行、
相交。( )
12、一条射线就是一个周角。( )
13、两点间线段最短。( )
×
×
√
√
×
×
×
√
在能围成三角形的一组线段下面的括号里画“√”
0.5cm
1.8cm
1cm
1cm
2.5cm
3cm
4cm
2cm
2cm
( )
( )
( )
√
填空
1、数一数,下图中有( )条直线,( )条射线,( )条线段。
1
8
6
2、在三角形ABC中AB=AC,∠C=500。BC边上取
一点D,已知∠ADC=720,∠BAD=( ).
3、将一长方形纸片,按如图的方式折叠,BC、BD为折痕,若∠ABC=300,则∠EBD的度数是( ).
画图
1、在A、B两村各修建一条小路与公路接通,要使两条小路最短,应该怎样修?请在图中画出来。
2、在甲、乙两村边上一条小河,在河边要建一个水站,要使水站到两村的距离和最短,水站应该建在哪?请在图中画出来。
公
路
四、课堂小结
平面图形的
认识与测量
(概念、特征)
点
线
面
体
几何图形的前世今生:
点动成线
线动成面
面动成体
一、引入复习
我们学过哪些平面图形和立体图形?你能对学过的图形进行分类吗?
问题
平面图形
封闭图形
不封闭图形
三角形
四边形
多边形
圆
平行四边形
直线、射线、线段、角
扇形
圆环
圆形
长方形
正方形
梯形
平行线、相交线
半圆形
扇环
图形都是由线组成,那么我们就从复习线开始复习几何图形。
二、整理复习
1.复习直线、射线、线段
(1)画一画
请同学们在纸上分别画出一条直线、射线、线段。
●
●
●
直线
射线
线段
线
线段:直线上两点间的一段叫做线段。
射线:把线段的一端无限延长,就得到一条射线。
直线:把线段的两端无限延长,就可以得到一条直线。
可以这样理解:线段取消一个端点之后就成为射线,射线再取消端点就成为直线。
A
B
线段、射线都是直线的一部分。
直线、射线和线段有什么区别?
端点 延伸 度量
直线 0 可以向两边无限延伸 不可测量
射线 1 可以向一边无限延伸 不可测量
线段 2 不可以延伸 可测量
经过一点可以画无数条直线。
从一点可以引出无数条射线。
经过两点只可以画一条直线。
经过两点只可以画一条线段。
关于距离:
两点之间的距离,线段最短。
直线外一点到这条直线的距离,垂直线段最短。
两条平行线之间的距离,垂直线段最短。
A
B
A
2.复习垂直和平行
同一平面内两条直线的位置关系有哪几种?
你能画出来吗?
平行
相交
重合
两条线:
同一平面内的两条直线,要么相交,要么互相平行。
(垂直是相交的特例)
同一平面内永不相交的两条直线叫做平行线,也可以说两条直线互相平行。(平行线间的距离处处相等)
相交
相交
互相平行
交点
两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
相交
交点
互相垂直
垂足
a ∥ b
a ⊥ b
平行线的画法;
A
l
O
l1
l2
思考
你能分别量出点O到直线l的距离、平行线l1与l2之间的距离吗?
从O点向直线l可以作无数条线段,在这些线段中,垂直线段最短。
用放大镜看角,角的边变长,大小没变
3.复习角
(1)角的定义:
从一个点引出的两条射线组成的图形叫做角
这个点叫做角的顶点,这两条射线叫做角的边
O
角通常用符号“∠”来表示。
边
顶点
边
比较下面∠1和∠2的大小,并说说角的大小与什么有关。
∠2>∠1,角的大小与两边张开的程度有关,与边的长短无关。
问题
角的两条边叉开得越大,角越大;叉开得越小,角就越小。角的大小与两条边的长短无关。
(2)角的分类:
锐角<直角<钝角<平角<周角
1周角=2平角=4直角
外刻度线
内刻度线
0刻度线
中心点
测量角的大小的工具是量角器。
把半圆分成180等份,每一份所对的角叫做 。
一度角
记作 “ 1°” 。
1°
量角的方法:
①把量角器放在角的上面,使量角器的中心与角的顶点重合。
②调整量角器,使“0”刻度线与角的一条边重合。
③读出角的另一边所对量角器上的度数,就是这个角的度数。
121°
121°
画角的方法:
①确定顶点,画一条射线;
②使量角器的中心与射线的端点重合,“0”刻度线与射线重合;
③在量角器上找出要画的角的度数的刻度,点上一个点;
④把射线的端点与刚才的点连起来。
60°
4.复习三角形
三角形的各部分名称:围成三角形的三条边叫做三角形的边;每两条边的交点叫做三角形的顶点;每两条边所形成的角叫做三角形的内角。(任意一个三角形都有3条边、3个顶点、3个角)
三角形的高:从三角形的一个顶点向它的对边作一条垂线,顶点与垂足之间的线段叫做三角形的高。任意一个三角形都有三条高;三角形的高和底是相互对应的。
等腰三角形
腰
腰
底
顶角
底角
底角
腰
顶角
腰
底角
底角
底
等腰直角三角形
腰
腰
底
顶角
底角
底角
等腰三角形
等腰三角形
有两条边相等的三角形叫做等腰三角形。其中相等的两条边叫做腰,另一条叫做底。两条腰的夹角叫做顶角,腰和底的夹角叫做底角,等腰三角形的两个底角度数相等。
边
边
边
等边三角形
(又叫正三角形)
三条边都相等的三角形叫做等边三角形,又叫正三角形。等边三角形的三条边长度相等,三个角的大小相等,都是60°。等边三角形是特殊的等腰三角形。
(1)三角形的分类
按边分
按角分
不等边三角形(三边都不相等)
(不是轴对称图形)
等腰
三角形
钝角三角形(有一个角是钝角)
锐角三角形(三个角都是锐角)
等边三角形或正三角形
(有三条边相等)(三个内角相等都是600)有3条对称轴
等腰三角形(有两条边相等)
(两个底角相等)有2条对称轴
直角三角形(有一个角是直角)
三角形
等边三角形一定是等腰三角形;
等腰三角形不一定是等边三角形。
有一个角是600 的等腰三角形
一定是等边三角形
一个三角形中最多有1个直角、1个
钝角;至少有2个锐角。
(2)三角形的特征
你知道三角形的特征有哪些?
1
具有稳定性(不易变形)
2
内角和180°
3
三角形的任意两边之和大于第三边
(任意两边之差小于第三边)
在直角三角形中,斜边永远大于任意一条直角边。
四边形的意义:在同一平面内,由四条线段首尾顺次相接围成的封闭图形叫做四边形。
四边形具有不稳定性(容易变形);四边形的四个内角和是360°。
5.复习四边形
长方形
两组对边分别平行并且相等,四个角都是直角的四边形叫做长方形。
长方形中较长的一组对边叫做长方形的长,较短的一组对边叫做长方形的宽。
长方形是特殊的平行四边形。
长
宽
长方形
长方形
长
宽
正方形
四条边相等,四个角都是直角的四边形叫做正方形。
正方形是特殊的长方形。
正方形
边长
平行四边形
两组对边分别平行的四边形叫做平行四边形。平行四边形对边的长度相等,对角的大小也相等。
从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,这条边叫做平行四边形的底。
底
高
平行四边形
高
底
梯 形
只有一组对边平行的四边形叫做梯形。
在梯形里,互相平行的一组对边叫做梯形的上底和下底,不平行的一组叫做梯形的腰,上底和下底之间的距离叫做梯形的高。
两腰相等的梯形叫做等腰梯形;有一个直角的梯形叫做直角梯形。
上底
下底
腰
腰
高
普通梯形
等腰梯形
直角梯形
四边形的分类
四边形
两组对边互不平行
只有一组对边平行
不规则四边形
梯形
两组对边分别平行
平行四边形
四个角
都是直角
长方形
四条边
都相等
正方形
四条边
都相等
菱形
四个角
都是直角
两腰相等
等腰梯形
有一个角是直角
直角梯形
也可以用下图分类:
四边形
不规则四边形
梯形
平行四边形
长方形
正方形
菱形
等腰梯形
直角梯形
还可以这样分类:
要画出一个圆,需要先确定什么?
圆心
半径
动手试试,任意画一个圆吧。
O
r
6.复习圆、圆环、扇形
圆心决定圆的位置,半径(直径)决定圆的大小。
问题
关于圆你都知道哪些知识呢?
一个圆有无数条半径,一般用字母r表示;有无数条直径,一般用字母d表示。
同一个圆内,直径的长度是半径的2倍,
即:d=2r。(直径是圆里最长的线段)
圆即是一种封闭的曲线图形;也是轴对称图形,它有无数条对称轴。
一
二
三
用圆规画圆时,针尖所在的点叫做圆心,一般用字母O表示。
连接圆心和圆上任意一点的线段
叫做半径,一般用字母r表示。
通过圆心并且两端都在圆上的线
段叫做直径,一般用字母d表示。
半径的长度就是圆规两个脚之间的距离。
圆的画法:
1、把圆规的两脚分开,定好两脚间
的距离(即半径)。
2、把有针尖的一只脚固定在一点(即
圆心上)。
3、把装有铅笔尖的一只脚旋转一周,
就画出一个圆。
定半径
定圆心
旋转一周
什么叫圆环?
在大圆中间挖去一个小圆,剩下的部分就形成了一个圆环,组成圆环的是两个同心圆。
圆环有什么特点?
1、同心圆。
2、两圆间的距离处处相等。
3、是轴对称图形,有无数条对称轴。
A
B
O
圆心角
半径
半径
弧
图上A、B两点之间的部分叫做弧,读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
顶点在圆心的角叫做圆心角。
◇ 复习扇形和扇形的各部分名称
1.一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。扇形是圆的一部分。
2.在同一个圆中,圆心角越大,扇形越大;在不同的圆中,圆心角相同的扇形,半径越大,扇形越大。
3.扇形的大小与圆心角和半径都有关。
巩固练习
1、 圆中心的一点叫做( ),一般用字母( )表示。
2、 连接圆心和圆上任意一点的线段叫做( ),一般用字母r表示。
3、通过圆心并且两端都在圆上的线段叫做( ),一般用字母d 表示。
4、一个圆内有( )条直径,( )条半径。并且( )条直径等于2 条半径。
5、圆是( )图形,有( )条对称轴。
圆心
O
半径
直径
无数
无数
1
轴对称
无数
填空:
6、圆是平面上的一种( )图形。圆的两条直径的交点是圆的( )。
7、把一个圆形纸片沿半径平均分成若干等份,拼成一个近似的长方形。则面积( ),周长( )。
8、圆中最长的线段是圆的( )。
9、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是( )、( )、( )。
不变
增加
直径
曲线
圆心
60cm
120cm
180cm
填空:
填空:
10、三角形的一个内角正好等于其余两个内角的和,这是一个( )三角形。
11、一个等腰三角形,它的顶角是72 ,它的底角是( )度。12、6时整,时针与分针组成的角的度数是( )
13、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是( )厘米,最少是( )厘米。
24、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是( )厘米。
直角
54
1800
21
18
2
1、大于90°的角叫钝角。( )
2、角的两条边越长,角就越大。( )
3、钟表的分针旋转一周,时针旋转30°。( )
4、可以画一条长10厘米的直线。( )
5、平角就是一条直线。( )
×
×
√
×
×
判 断
6、两条直线不相交就平行。( )
7、直线的两端可以无限延长。( )
8、一个20°的角用2倍放大镜看,会看到一个40°的
角。( )
9、一个平角减去一个锐角,得到一个钝角。( )
10、射线比直线短。( )
11、两条直线的位置关系可分为三种:垂直、平行、
相交。( )
12、一条射线就是一个周角。( )
13、两点间线段最短。( )
×
×
√
√
×
×
×
√
在能围成三角形的一组线段下面的括号里画“√”
0.5cm
1.8cm
1cm
1cm
2.5cm
3cm
4cm
2cm
2cm
( )
( )
( )
√
填空
1、数一数,下图中有( )条直线,( )条射线,( )条线段。
1
8
6
2、在三角形ABC中AB=AC,∠C=500。BC边上取
一点D,已知∠ADC=720,∠BAD=( ).
3、将一长方形纸片,按如图的方式折叠,BC、BD为折痕,若∠ABC=300,则∠EBD的度数是( ).
画图
1、在A、B两村各修建一条小路与公路接通,要使两条小路最短,应该怎样修?请在图中画出来。
2、在甲、乙两村边上一条小河,在河边要建一个水站,要使水站到两村的距离和最短,水站应该建在哪?请在图中画出来。
公
路
四、课堂小结
