2022-2023学年苏科版八年级数学上册2.5 等腰三角形的轴对称性(1)课件(共16张PPT)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册2.5 等腰三角形的轴对称性(1)课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 129.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 07:06:34 | ||
图片预览




文档简介
(共16张PPT)
2.5 等腰三角形的轴对称性(1)
八年级(上册)
初中数学
1.说出线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
∵PO⊥AB,AO=BO
∴PA=PB
2
1
l
P
O
B
A
符号语言:
自主检测
腰
腰
顶角
底边
(
)
)
底角
底角
A
B
C
有两边相等的三角形叫等腰三角形.
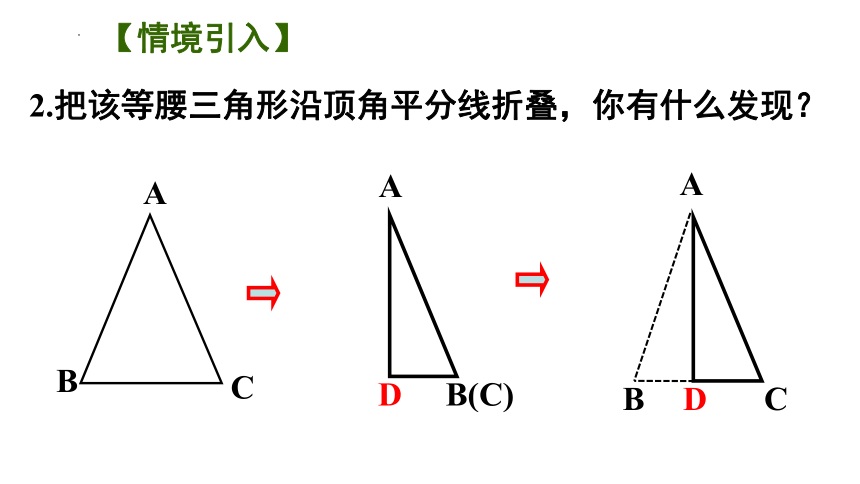
2.把该等腰三角形沿顶角平分线折叠,你有什么发现?
【情境引入】
A
B(C)
D
A
C
D
B
A
B
C
【探究活动】
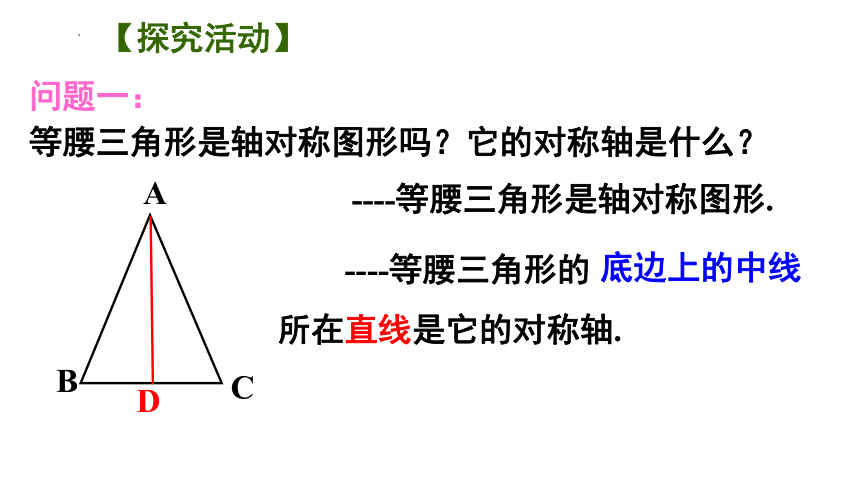
问题一:
等腰三角形是轴对称图形吗?它的对称轴是什么?
A
B
C
----等腰三角形是轴对称图形.
----等腰三角形的 顶角平分线 所在直线是它的对称轴.
D
底边上的高
底边上的中线
【探究活动】
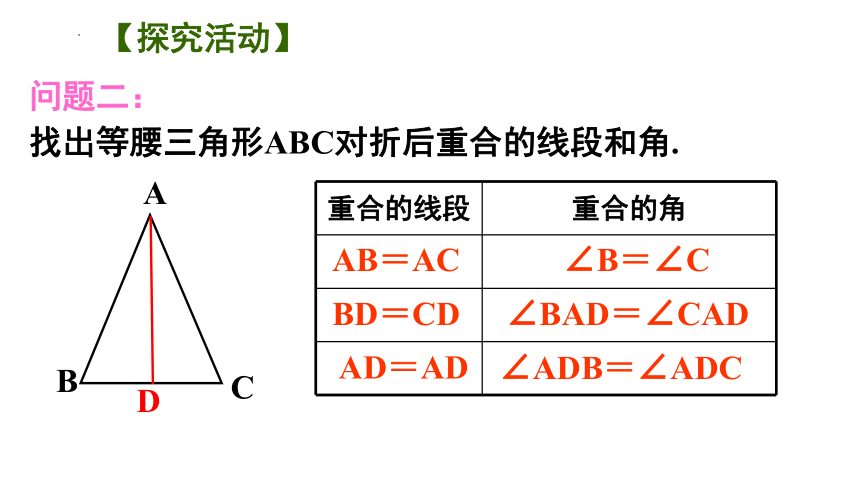
问题二:
找出等腰三角形ABC对折后重合的线段和角.
A
B
C
重合的线段 重合的角
D
AB=AC
BD=CD
AD=AD
∠B=∠C
∠BAD=∠CAD
∠ADB=∠ADC
【探究活动】
问题三:由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想.
A
B
C
D
1.等腰三角形是轴对称图形;它的顶角平分线(底边上的高、中线)所在直线是它的对称轴.
2.等腰三角形的两个底角相等.
3.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
【归纳总结】
1.等腰三角形的两底角相等.
A
B
C
D
我们有如下定理:
2.等腰三角形底边上的高线、中线及顶角平分线重合.
(简称 “等边对等角”)
(简称 “三线合一”)
练一练:
1.在△ABC中,AB=AC.
⑴ 如果∠B=70°,那么∠C=___,∠A=____.
⑵ 如果∠A=70°,那么∠B=____,∠C= ___.
⑶ 如果有一个角等于120°,
那么∠A=___ °,∠B=___ °,∠C =___ °.
⑷ 如果有一个角等于50°,那么另两个角等于多少度?
(5) 等腰△ABC中, ∠A=50°,则∠B=_______.
2.如图的房屋人字梁架中,AB=AC ,AD⊥BC, ∠BAC=110°,求∠B、∠C 、∠BAD、∠CAD的度数.
练一练:
(3)等腰三角形的周长为10,一边长为4,
那么另外两边长为 .
3.(1)等腰三角形的两边长分别为3cm和6cm,
则它的周长为______.
(2)等腰三角形的两边长分别为5cm和6cm,
则它的周长为______.
练一练:
【操作尝试】
按下列作法,用直尺和圆规作等腰三角形ABC,
使底边BC=a,高AD=h.
【例题讲解 】
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,求证: ∠ADB=∠BAC.
A
B
C
D
1.如图:△ABC中,AB=AC,AD=AE.
求证:BE=CD.
E
D
C
B
A
G
练一练:
2.如图,AB = AC = AD,且AD∥BC,
∠C =2∠D吗?试说明理由.
A
B
C
D
练一练:
A
B
C
D
E
3.如图,在△ABC中, AB=AC, △ABD与△AEC都是等边三角形,且∠DAE=∠DBC, 求△ABC的三个内角的度数.
练一练:
小结:
2.等腰三角形是轴对称图形,顶角平分线(或底边上的中线、底边上的高)所在直线是它的对称轴.
1.有两条边相等的三角形,叫做等腰三角形.
(1)等腰三角形的两个底角相等(等边对等角).
3.等腰三角形的性质:
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(三线合一)
2.5 等腰三角形的轴对称性(1)
八年级(上册)
初中数学
1.说出线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
∵PO⊥AB,AO=BO
∴PA=PB
2
1
l
P
O
B
A
符号语言:
自主检测
腰
腰
顶角
底边
(
)
)
底角
底角
A
B
C
有两边相等的三角形叫等腰三角形.
2.把该等腰三角形沿顶角平分线折叠,你有什么发现?
【情境引入】
A
B(C)
D
A
C
D
B
A
B
C
【探究活动】
问题一:
等腰三角形是轴对称图形吗?它的对称轴是什么?
A
B
C
----等腰三角形是轴对称图形.
----等腰三角形的 顶角平分线 所在直线是它的对称轴.
D
底边上的高
底边上的中线
【探究活动】
问题二:
找出等腰三角形ABC对折后重合的线段和角.
A
B
C
重合的线段 重合的角
D
AB=AC
BD=CD
AD=AD
∠B=∠C
∠BAD=∠CAD
∠ADB=∠ADC
【探究活动】
问题三:由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想.
A
B
C
D
1.等腰三角形是轴对称图形;它的顶角平分线(底边上的高、中线)所在直线是它的对称轴.
2.等腰三角形的两个底角相等.
3.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
【归纳总结】
1.等腰三角形的两底角相等.
A
B
C
D
我们有如下定理:
2.等腰三角形底边上的高线、中线及顶角平分线重合.
(简称 “等边对等角”)
(简称 “三线合一”)
练一练:
1.在△ABC中,AB=AC.
⑴ 如果∠B=70°,那么∠C=___,∠A=____.
⑵ 如果∠A=70°,那么∠B=____,∠C= ___.
⑶ 如果有一个角等于120°,
那么∠A=___ °,∠B=___ °,∠C =___ °.
⑷ 如果有一个角等于50°,那么另两个角等于多少度?
(5) 等腰△ABC中, ∠A=50°,则∠B=_______.
2.如图的房屋人字梁架中,AB=AC ,AD⊥BC, ∠BAC=110°,求∠B、∠C 、∠BAD、∠CAD的度数.
练一练:
(3)等腰三角形的周长为10,一边长为4,
那么另外两边长为 .
3.(1)等腰三角形的两边长分别为3cm和6cm,
则它的周长为______.
(2)等腰三角形的两边长分别为5cm和6cm,
则它的周长为______.
练一练:
【操作尝试】
按下列作法,用直尺和圆规作等腰三角形ABC,
使底边BC=a,高AD=h.
【例题讲解 】
例1 如图,在△ABC中,AB=AC,点D在BC上,且AD=BD,求证: ∠ADB=∠BAC.
A
B
C
D
1.如图:△ABC中,AB=AC,AD=AE.
求证:BE=CD.
E
D
C
B
A
G
练一练:
2.如图,AB = AC = AD,且AD∥BC,
∠C =2∠D吗?试说明理由.
A
B
C
D
练一练:
A
B
C
D
E
3.如图,在△ABC中, AB=AC, △ABD与△AEC都是等边三角形,且∠DAE=∠DBC, 求△ABC的三个内角的度数.
练一练:
小结:
2.等腰三角形是轴对称图形,顶角平分线(或底边上的中线、底边上的高)所在直线是它的对称轴.
1.有两条边相等的三角形,叫做等腰三角形.
(1)等腰三角形的两个底角相等(等边对等角).
3.等腰三角形的性质:
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.(三线合一)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
