图形的运动(课件)六年级下册数学人教版(共26张PPT)
文档属性
| 名称 | 图形的运动(课件)六年级下册数学人教版(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
图形的运动
图形变换:
平移、旋转、轴对称、放大、缩小是五种图形变换的方式。
几何变换中最重要的是全等变换与相似变换。
能够保持图形的形状和大小不变,只是位置发生改变的变换就是全等变换。在全等变换中,原图形任何两点之间的距离,都等于新图形中两对应点之间的距离,所以又称为保距变换。
能够保持图形的形状不变,而只改变图形大小的变换就是相似变换。在相似变换中,原图形中所有角的大小都保持不变,所以又称为保角变换。
图形变换:
变换
全等变换
相似变换
平移变换
旋转变换
轴对称变换
图形的放大
图形的缩小
(形状不变,
大小改变。)
(形状不变,
大小不变。)
一、引入复习
想一想:这些图案用到了什么数学知识?
轴对称、平移、旋转、图形的放大与缩小
二、整理复习
1.轴对称图形、轴对称
什么是轴对称图形?什么叫对称轴?
轴对称图形:一个图形沿着一条直线对折,对折后折痕两边的部分完全重合。
对称轴:折痕所在的直线;在画图时两端必须出头。
轴对称:把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形关于这条直线对称,叫做轴对称。这条直线叫做对称轴。
对折后重合的点叫对称点(对应点),对称点名称不能和原来的一样。对称点之间的连线与对称轴互相垂直,对称点到对称轴间的距离相等。
轴对称图形与轴对称的区别
轴对称图形
(指一个图形)
轴对称
(指两个图形)
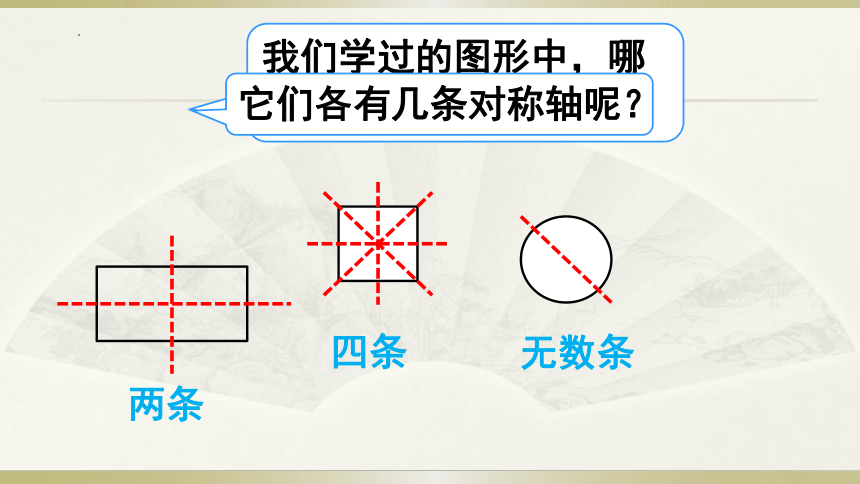
我们学过的图形中,哪些是轴对称图行呢?
它们各有几条对称轴呢?
两条
四条
无数条
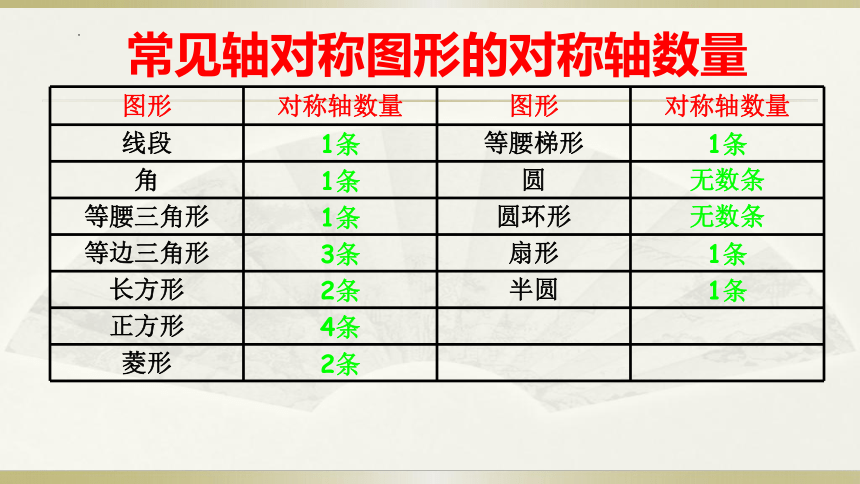
图形 对称轴数量 图形 对称轴数量
线段 1条 等腰梯形 1条
角 1条 圆 无数条
等腰三角形 1条 圆环形 无数条
等边三角形 3条 扇形 1条
长方形 2条 半圆 1条
正方形 4条
菱形 2条
常见轴对称图形的对称轴数量
2.平移
1.平移的方向
2.平移的距离
平移的两要素?
平移:物体或图形在同一个
平面内沿直线运动,而本身
没有发生大小、形状和方向
的改变,像这样的物体或图
形所做的运动叫做平移。
生活中的平移现象
垂直升降电梯
汽车在公路上行驶
你还能想到哪些?
推拉窗
3.旋转
什么是旋转呢?
旋转:把一个图形绕着某一固定点按顺时针或逆时针方向转动一定角度的过程。
左逆右顺
图形的旋转不改变图形的形状和大小。只是图形的位置发生改变。
旋转三要素?
旋转中心
旋转方向
旋转角度
生活中的旋转现象
风车
摩天轮
旋转门
生活中的旋转现象还有哪些呢?
4.放大与缩小
图形怎样放大?怎样缩小?
长和宽同时放大或缩小相同的倍数。
按一定比例,将一个图形放大或缩小,叫做图形的缩放。(缩放后的图统称为原图形的相似图)
图形的放大和缩小
图形的放大与缩小,改变了图形的大小,图形的形状没变。
相同点
不同点
1、边的长度按一定的倍数放大或缩小,图形的 大小发生变化。图形的形状不变。
2、比的前项表示变化后的长度,比的后项表示 原来的长度。
比值大于1(如2:1),表示图形放大。
比值小于1(如1:3),表示图形缩小。
图形的放大与缩小的区别与联系
这些图案分别运用了哪种图形运动的知识?
旋转45°
放大
平移
讨论
哪些运动不改变图形的形状和大小?哪些运动只改变大小,不改变形状?
结论
平移、轴对称、旋转不改变图形的形状和大小;图形的放大与缩小只改变大小,不改变形状。
图形最基本的运动方式:轴对称、平移、旋转
三、巩固深化
做一做
图中A→B→C→D是怎样变过来的?
A平移得到B,B平移后逆时针旋转90°得到C,C平移后逆时针旋转90°得到D。
下面哪些图形是轴对称图形?画出它们的对称轴。
第1、2幅图不是轴对称图形,第3、4幅图是轴对称图形。
根据给定的对称轴画出图形的另一半。
画一画
(1)小旗子向左平移8格后的图形。
(2)小旗子绕O点按顺时针方向旋转90°后的图形。
(3)小旗子按2:1扩大后的图形。
0
一个直角三角形ABC的两条直角边长分别是3cm和4cm,把它按2:1放大之后得到的三角形DEF。三角形ABC与DEF的周长之比是多少?面积之比呢?
周长之比1:2
面积之比1:4
四、课堂小结
图形的运动
图形变换:
平移、旋转、轴对称、放大、缩小是五种图形变换的方式。
几何变换中最重要的是全等变换与相似变换。
能够保持图形的形状和大小不变,只是位置发生改变的变换就是全等变换。在全等变换中,原图形任何两点之间的距离,都等于新图形中两对应点之间的距离,所以又称为保距变换。
能够保持图形的形状不变,而只改变图形大小的变换就是相似变换。在相似变换中,原图形中所有角的大小都保持不变,所以又称为保角变换。
图形变换:
变换
全等变换
相似变换
平移变换
旋转变换
轴对称变换
图形的放大
图形的缩小
(形状不变,
大小改变。)
(形状不变,
大小不变。)
一、引入复习
想一想:这些图案用到了什么数学知识?
轴对称、平移、旋转、图形的放大与缩小
二、整理复习
1.轴对称图形、轴对称
什么是轴对称图形?什么叫对称轴?
轴对称图形:一个图形沿着一条直线对折,对折后折痕两边的部分完全重合。
对称轴:折痕所在的直线;在画图时两端必须出头。
轴对称:把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形关于这条直线对称,叫做轴对称。这条直线叫做对称轴。
对折后重合的点叫对称点(对应点),对称点名称不能和原来的一样。对称点之间的连线与对称轴互相垂直,对称点到对称轴间的距离相等。
轴对称图形与轴对称的区别
轴对称图形
(指一个图形)
轴对称
(指两个图形)
我们学过的图形中,哪些是轴对称图行呢?
它们各有几条对称轴呢?
两条
四条
无数条
图形 对称轴数量 图形 对称轴数量
线段 1条 等腰梯形 1条
角 1条 圆 无数条
等腰三角形 1条 圆环形 无数条
等边三角形 3条 扇形 1条
长方形 2条 半圆 1条
正方形 4条
菱形 2条
常见轴对称图形的对称轴数量
2.平移
1.平移的方向
2.平移的距离
平移的两要素?
平移:物体或图形在同一个
平面内沿直线运动,而本身
没有发生大小、形状和方向
的改变,像这样的物体或图
形所做的运动叫做平移。
生活中的平移现象
垂直升降电梯
汽车在公路上行驶
你还能想到哪些?
推拉窗
3.旋转
什么是旋转呢?
旋转:把一个图形绕着某一固定点按顺时针或逆时针方向转动一定角度的过程。
左逆右顺
图形的旋转不改变图形的形状和大小。只是图形的位置发生改变。
旋转三要素?
旋转中心
旋转方向
旋转角度
生活中的旋转现象
风车
摩天轮
旋转门
生活中的旋转现象还有哪些呢?
4.放大与缩小
图形怎样放大?怎样缩小?
长和宽同时放大或缩小相同的倍数。
按一定比例,将一个图形放大或缩小,叫做图形的缩放。(缩放后的图统称为原图形的相似图)
图形的放大和缩小
图形的放大与缩小,改变了图形的大小,图形的形状没变。
相同点
不同点
1、边的长度按一定的倍数放大或缩小,图形的 大小发生变化。图形的形状不变。
2、比的前项表示变化后的长度,比的后项表示 原来的长度。
比值大于1(如2:1),表示图形放大。
比值小于1(如1:3),表示图形缩小。
图形的放大与缩小的区别与联系
这些图案分别运用了哪种图形运动的知识?
旋转45°
放大
平移
讨论
哪些运动不改变图形的形状和大小?哪些运动只改变大小,不改变形状?
结论
平移、轴对称、旋转不改变图形的形状和大小;图形的放大与缩小只改变大小,不改变形状。
图形最基本的运动方式:轴对称、平移、旋转
三、巩固深化
做一做
图中A→B→C→D是怎样变过来的?
A平移得到B,B平移后逆时针旋转90°得到C,C平移后逆时针旋转90°得到D。
下面哪些图形是轴对称图形?画出它们的对称轴。
第1、2幅图不是轴对称图形,第3、4幅图是轴对称图形。
根据给定的对称轴画出图形的另一半。
画一画
(1)小旗子向左平移8格后的图形。
(2)小旗子绕O点按顺时针方向旋转90°后的图形。
(3)小旗子按2:1扩大后的图形。
0
一个直角三角形ABC的两条直角边长分别是3cm和4cm,把它按2:1放大之后得到的三角形DEF。三角形ABC与DEF的周长之比是多少?面积之比呢?
周长之比1:2
面积之比1:4
四、课堂小结
