人教版八年级上册13.3.2等边三角形(第1课时)课件(共21张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.2等边三角形(第1课时)课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 08:07:21 | ||
图片预览





文档简介
(共21张PPT)
13.3.2等边三角形
第1课时
学习目标
1. 掌握等边三角形的概念,探索并掌握等边三角形的性质、判定方法,及定理的证明。
2. 等边三角形性质和判定定理的运用。
3. 经过运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维。
4. 经过探索、猜想、证明、归纳等数学活动过程,发展逻辑推理能力。
重点
等边三角形
难点
应用新知
巩固新知
课堂小结
布置作业
名称 图形 定义 性质 判定
等腰三角形 有两条边相等的三角形叫做等腰三角形 两腰相等 两边相等
等边对等角 等角对等边
三线合一
轴对称图形
前面我们一起研究了等腰三角形,回顾一下,我们是从哪些方面来研究等腰三角形的呢?
探究新知
创设情境
复习回顾
定义
性质
判定
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
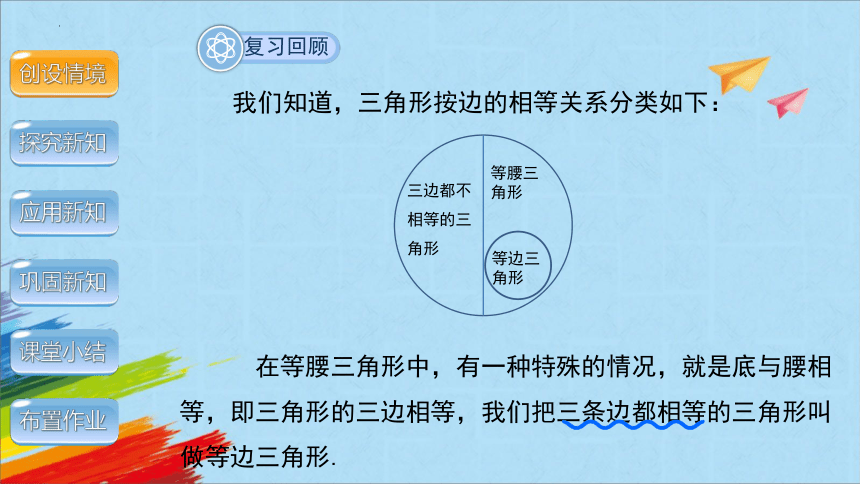
我们知道,三角形按边的相等关系分类如下:
三边都不相等的三角形
等腰三角形
等边三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫做等边三角形.
复习回顾
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
把等腰三角形的性质用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
性质 边 两腰相等 等边三角形三边相等
角 (等角对等边)
等边三角形的三个内角都相等
猜想
讨论
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
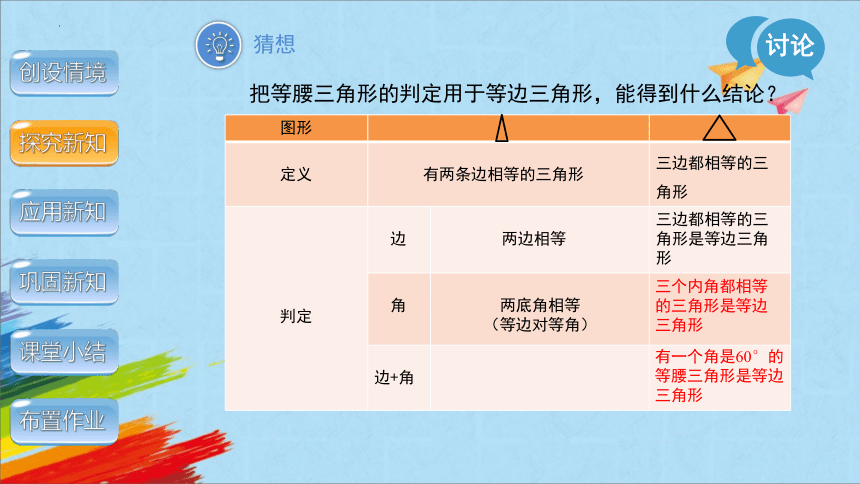
把等腰三角形的判定用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
判定 边 两边相等 三边都相等的三角形是等边三角形
角 两底角相等 (等边对等角)
边+角
三个内角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
猜想
讨论
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知:△ABC是等边三角形。
求证:∠A =∠B=∠C
A
B
C
证明:∵△ABC是等边三角形
∴BC=AC,BC=AB
∴∠A=∠B,∠A=∠C
∴∠A =∠B=∠C
∵∠A+∠B+∠C=180°
∴∠A =60°
∴∠A=∠B=∠C=60°
试着做做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
等边三角形的三个内角都相等,并且每一个角都等于60°
性质1:
符号语言:
∵△ABC是等边三角形
∴∠A=∠B=∠C=60°
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
等边三角形除了用定义(即用边)来判定外,能否用角来判定呢?
下面我们来证明
一起探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知:在△ABC中,∠A=∠B=∠C
求证:△ABC是等边三角形
A
B
C
证明:∵∠A=∠B,∠B=∠C,
∴BC=AC,AC=AB(等角对等边)
∴AB=BC=AC
∴△ABC是等边三角形
试着做做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
,
三个角都相等的三角形是等边三角形。
等边三角形的判定定理1:
符号语言表示:
在△ABC中,
∵∠A=∠B=∠C
∴△ABC是等边三角形
归纳
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知:在△ABC中,AC=BC且∠A=60°
求证:△ABC是等边三角形
∠C=60°
证明:
∵AC=BC
∴∠A=∠B
又∵∠A=60°
∴∠B=60°
A
B
C
∴△ABC是等边三角形
试着做做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
有一个角为60°的等腰三角形是等边三角形。
等边三角形的判定定理2:
符号语言表示:
在△ABC中,
∵BC=AC,∠A=60°,
∴△ABC是等边三角形
归纳
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E。求证:△ADE是等边三角形
∴∠ADE=∠B,∠AED=∠C
证明:
∵△ABC是等边三角形,
∵DE∥BC,
∴∠A=∠ADE=∠AED
∴△ADE是等边三角形
∴∠A=∠B=∠C
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,△ABC的边BC上有D、E两点,且BD=DE=EC=AD=AE,则∠BAC=_____
120°
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.下面给出的几种三角形:
A.4个 B.3个 C.2个 D.1个
①有两个角是60°的三角形;
②三个外角都相等的三角形;③一边上的高也是这边上的中线的三角形;④有一个外角120°的等腰三角形
其中一定是等边三角形的有( )
B
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( )
A.9 B.8 C.6 D.7
B
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
性质1:
定义:
等边三角形是三边都相等的特殊的等腰三角形
等边三角形的三个内角都相等,并且每一个角都等于60°
等边三角形
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
等边三角形
判定2:
判定1:
三个角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
布置作业
教科书第80页习题
1,2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
13.3.2等边三角形
第1课时
学习目标
1. 掌握等边三角形的概念,探索并掌握等边三角形的性质、判定方法,及定理的证明。
2. 等边三角形性质和判定定理的运用。
3. 经过运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维。
4. 经过探索、猜想、证明、归纳等数学活动过程,发展逻辑推理能力。
重点
等边三角形
难点
应用新知
巩固新知
课堂小结
布置作业
名称 图形 定义 性质 判定
等腰三角形 有两条边相等的三角形叫做等腰三角形 两腰相等 两边相等
等边对等角 等角对等边
三线合一
轴对称图形
前面我们一起研究了等腰三角形,回顾一下,我们是从哪些方面来研究等腰三角形的呢?
探究新知
创设情境
复习回顾
定义
性质
判定
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
我们知道,三角形按边的相等关系分类如下:
三边都不相等的三角形
等腰三角形
等边三角形
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫做等边三角形.
复习回顾
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
把等腰三角形的性质用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
性质 边 两腰相等 等边三角形三边相等
角 (等角对等边)
等边三角形的三个内角都相等
猜想
讨论
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
把等腰三角形的判定用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
判定 边 两边相等 三边都相等的三角形是等边三角形
角 两底角相等 (等边对等角)
边+角
三个内角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
猜想
讨论
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知:△ABC是等边三角形。
求证:∠A =∠B=∠C
A
B
C
证明:∵△ABC是等边三角形
∴BC=AC,BC=AB
∴∠A=∠B,∠A=∠C
∴∠A =∠B=∠C
∵∠A+∠B+∠C=180°
∴∠A =60°
∴∠A=∠B=∠C=60°
试着做做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
等边三角形的三个内角都相等,并且每一个角都等于60°
性质1:
符号语言:
∵△ABC是等边三角形
∴∠A=∠B=∠C=60°
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
等边三角形除了用定义(即用边)来判定外,能否用角来判定呢?
下面我们来证明
一起探究
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知:在△ABC中,∠A=∠B=∠C
求证:△ABC是等边三角形
A
B
C
证明:∵∠A=∠B,∠B=∠C,
∴BC=AC,AC=AB(等角对等边)
∴AB=BC=AC
∴△ABC是等边三角形
试着做做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
,
三个角都相等的三角形是等边三角形。
等边三角形的判定定理1:
符号语言表示:
在△ABC中,
∵∠A=∠B=∠C
∴△ABC是等边三角形
归纳
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
已知:在△ABC中,AC=BC且∠A=60°
求证:△ABC是等边三角形
∠C=60°
证明:
∵AC=BC
∴∠A=∠B
又∵∠A=60°
∴∠B=60°
A
B
C
∴△ABC是等边三角形
试着做做
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
有一个角为60°的等腰三角形是等边三角形。
等边三角形的判定定理2:
符号语言表示:
在△ABC中,
∵BC=AC,∠A=60°,
∴△ABC是等边三角形
归纳
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
典型例题
如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E。求证:△ADE是等边三角形
∴∠ADE=∠B,∠AED=∠C
证明:
∵△ABC是等边三角形,
∵DE∥BC,
∴∠A=∠ADE=∠AED
∴△ADE是等边三角形
∴∠A=∠B=∠C
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,△ABC的边BC上有D、E两点,且BD=DE=EC=AD=AE,则∠BAC=_____
120°
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.下面给出的几种三角形:
A.4个 B.3个 C.2个 D.1个
①有两个角是60°的三角形;
②三个外角都相等的三角形;③一边上的高也是这边上的中线的三角形;④有一个外角120°的等腰三角形
其中一定是等边三角形的有( )
B
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,在△ABC中,∠BAC=120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC的长为( )
A.9 B.8 C.6 D.7
B
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
性质1:
定义:
等边三角形是三边都相等的特殊的等腰三角形
等边三角形的三个内角都相等,并且每一个角都等于60°
等边三角形
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
等边三角形
判定2:
判定1:
三个角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
布置作业
教科书第80页习题
1,2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
