12.1 全等三角形 课件(共21张PPT)
文档属性
| 名称 | 12.1 全等三角形 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 353.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 06:22:53 | ||
图片预览




文档简介
(共21张PPT)
第十二章 全等三角形
12.1
全等三角形
情景导入-合作探究-当堂演练-板书设计
12.1 全等三角形
情景导入
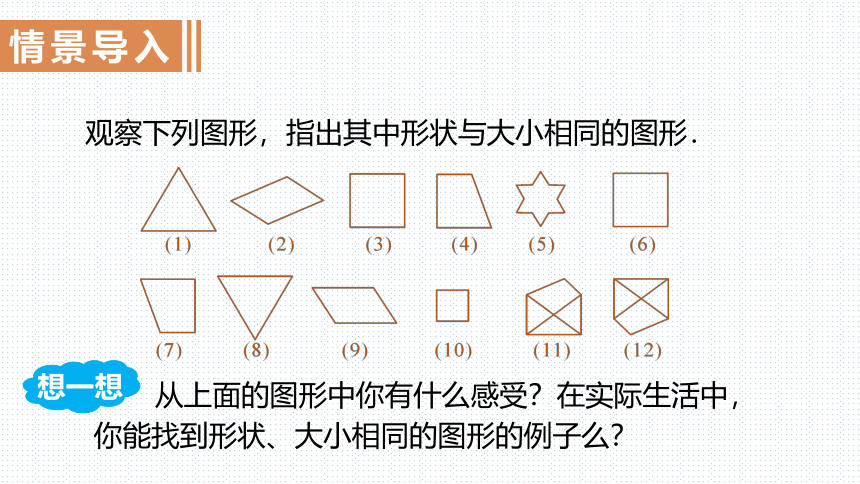
观察下列图形,指出其中形状与大小相同的图形.
从上面的图形中你有什么感受?在实际生活中,你能找到形状、大小相同的图形的例子么?
想一想
合作探究
知识板块一 全等形
国旗的形状和大小一样吗
平移
国徽的形状和大小一样吗
旋转
小猫的形状和大小一样吗
翻折
一个图形经过平移、翻折、旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形___________ .
完全重合
形状
大小
形状、大小相同的图形放在一起能够完全重合.
能够完全重合的两个图形叫做全等形.
合作探究
知识板块二 全等三角形及对应元素
能够完全重合的两个三角形,叫做全等三角形.
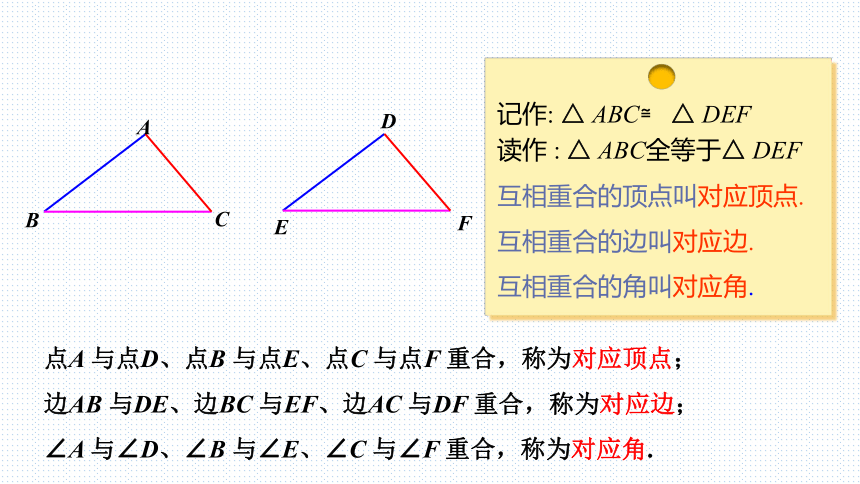
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
记作: △ ABC≌ △ DEF
读作 : △ ABC全等于△ DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
A
B
C
E
D
F
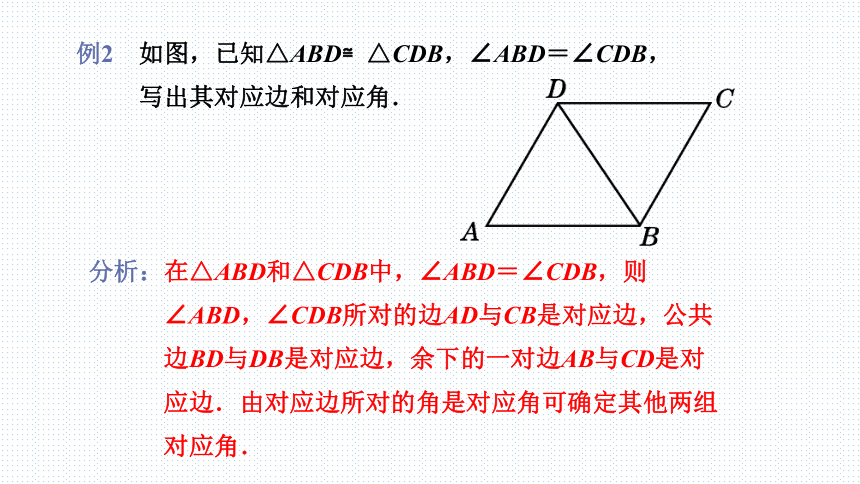
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB,
写出其对应边和对应角.
分析:在△ABD和△CDB中,∠ABD=∠CDB,则
∠ABD,∠CDB所对的边AD与CB是对应边,公共
边BD与DB是对应边,余下的一对边AB与CD是对
应边.由对应边所对的角是对应角可确定其他两组
对应角.
解:BD与DB,AD与CB,AB与CD是对应边;
∠A与∠C,∠ABD与∠CDB,∠ADB与∠CBD是对应角.
对应元素的确定方法:
(1)字母顺序确定法:根据书写规范,按照对应顶点确定对应边、对应角,如△CAB≌△FDE,则AB与DE、AC与DF、BC与EF是对应边,∠A和∠D、∠B和∠E、∠C和∠F是对应角;
(2)图形位置确定法:①公共边一定是对应边,②公共角一定是对应角;③对顶角一定是对应角;
(3)图形大小确定法:两个全等三角形的最大的边(角)是对应边 (角),最小的边(角)是对应边(角).
合作探究
知识板块三 全等三角形的性质
图中,△ABC≌△DEF,对应边有什么关系?
对应角有什么关系?
A
B
C
E
D
F
全等三角形的性质:
全等三角形的对应边相等,
全等三角形的对应角相等。
还具备:全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
例3 如图,已知点A,D,B,F在同一条直线上,
△ABC≌△FDE,AB=8 cm,BD=6 cm.
求FB的长.
分析:由全等三角形的性质知AB=FD,由等式的性质可得:
AD=FB,所以要求FB的长,只需求AD的长.
解:∵△ABC≌△FDE,∴ AB=FD.
∴ AB-DB=FD-DB,即AD=FB.
∵AB=8 cm,BD=6 cm,
∴AD=AB-DB=8-6= 2(cm).
∴FB=AD=2cm.
在应用全等三角形性质时,要先确定两个条件:
①两个三角形全等;②找对应元素;
全等三角形的性质是证明线段、角相等的常用方法.
当堂演练
1.下列四组图形中,是全等图形的一组是( )
D
当堂演练
2.若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A.BC=EF B.∠B=∠D
C.∠C=∠F D.AC=EF
A
当堂演练
3.如图,将△ABC沿BC所在的直线平移到△A′B′C′的位置,则△ABC________△A′B′C′,图中∠A与
________ ,∠B与________ ,∠ACB与________
是对应角.
≌
∠A′
∠ A′B′C′
∠C′
当堂演练
4.如图,△ABC≌△DEF,∠B=30°,∠A=50°,BF=2,求∠DFE的度数与EC的长.
解:∵∠B+∠A+∠ACB=180°,
∴∠ACB=180°-∠A-∠B
=180°-50°-30°=100°.
又∵△ABC≌△DEF,
∴∠DFE=∠ACB=100°,EF=CB,
∴EF-CF=CB-CF,即CE=BF=2.
板书设计
1.能够完全重合的两个图形叫做全等形.两个图形是否全等只与这个图形的形状和大小有关,与位置无关.
2.能够完全重合的两个三角形叫做全等三角形.平移、翻折、旋转前后的图形全等.把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角,全等用符号“≌”表示,读作“全等于”,记两个三角形全等时,表示对应顶点的字母要写在对应位置上.
第十二章 全等三角形
12.1
全等三角形
情景导入-合作探究-当堂演练-板书设计
12.1 全等三角形
情景导入
观察下列图形,指出其中形状与大小相同的图形.
从上面的图形中你有什么感受?在实际生活中,你能找到形状、大小相同的图形的例子么?
想一想
合作探究
知识板块一 全等形
国旗的形状和大小一样吗
平移
国徽的形状和大小一样吗
旋转
小猫的形状和大小一样吗
翻折
一个图形经过平移、翻折、旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形___________ .
完全重合
形状
大小
形状、大小相同的图形放在一起能够完全重合.
能够完全重合的两个图形叫做全等形.
合作探究
知识板块二 全等三角形及对应元素
能够完全重合的两个三角形,叫做全等三角形.
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
记作: △ ABC≌ △ DEF
读作 : △ ABC全等于△ DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
A
B
C
E
D
F
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB,
写出其对应边和对应角.
分析:在△ABD和△CDB中,∠ABD=∠CDB,则
∠ABD,∠CDB所对的边AD与CB是对应边,公共
边BD与DB是对应边,余下的一对边AB与CD是对
应边.由对应边所对的角是对应角可确定其他两组
对应角.
解:BD与DB,AD与CB,AB与CD是对应边;
∠A与∠C,∠ABD与∠CDB,∠ADB与∠CBD是对应角.
对应元素的确定方法:
(1)字母顺序确定法:根据书写规范,按照对应顶点确定对应边、对应角,如△CAB≌△FDE,则AB与DE、AC与DF、BC与EF是对应边,∠A和∠D、∠B和∠E、∠C和∠F是对应角;
(2)图形位置确定法:①公共边一定是对应边,②公共角一定是对应角;③对顶角一定是对应角;
(3)图形大小确定法:两个全等三角形的最大的边(角)是对应边 (角),最小的边(角)是对应边(角).
合作探究
知识板块三 全等三角形的性质
图中,△ABC≌△DEF,对应边有什么关系?
对应角有什么关系?
A
B
C
E
D
F
全等三角形的性质:
全等三角形的对应边相等,
全等三角形的对应角相等。
还具备:全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
例3 如图,已知点A,D,B,F在同一条直线上,
△ABC≌△FDE,AB=8 cm,BD=6 cm.
求FB的长.
分析:由全等三角形的性质知AB=FD,由等式的性质可得:
AD=FB,所以要求FB的长,只需求AD的长.
解:∵△ABC≌△FDE,∴ AB=FD.
∴ AB-DB=FD-DB,即AD=FB.
∵AB=8 cm,BD=6 cm,
∴AD=AB-DB=8-6= 2(cm).
∴FB=AD=2cm.
在应用全等三角形性质时,要先确定两个条件:
①两个三角形全等;②找对应元素;
全等三角形的性质是证明线段、角相等的常用方法.
当堂演练
1.下列四组图形中,是全等图形的一组是( )
D
当堂演练
2.若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,则下列结论错误的是( )
A.BC=EF B.∠B=∠D
C.∠C=∠F D.AC=EF
A
当堂演练
3.如图,将△ABC沿BC所在的直线平移到△A′B′C′的位置,则△ABC________△A′B′C′,图中∠A与
________ ,∠B与________ ,∠ACB与________
是对应角.
≌
∠A′
∠ A′B′C′
∠C′
当堂演练
4.如图,△ABC≌△DEF,∠B=30°,∠A=50°,BF=2,求∠DFE的度数与EC的长.
解:∵∠B+∠A+∠ACB=180°,
∴∠ACB=180°-∠A-∠B
=180°-50°-30°=100°.
又∵△ABC≌△DEF,
∴∠DFE=∠ACB=100°,EF=CB,
∴EF-CF=CB-CF,即CE=BF=2.
板书设计
1.能够完全重合的两个图形叫做全等形.两个图形是否全等只与这个图形的形状和大小有关,与位置无关.
2.能够完全重合的两个三角形叫做全等三角形.平移、翻折、旋转前后的图形全等.把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角,全等用符号“≌”表示,读作“全等于”,记两个三角形全等时,表示对应顶点的字母要写在对应位置上.
