2022_2023学年新教材高中数学第六章平面向量初步6.1平面向量及其线性运算6.1.1向量的概念学案新人教B版必修第二册
文档属性
| 名称 | 2022_2023学年新教材高中数学第六章平面向量初步6.1平面向量及其线性运算6.1.1向量的概念学案新人教B版必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 302.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览




文档简介
6.1 平面向量及其线性运算
6.1.1 向量的概念
【课程标准】
(1)通过对力、速度、位移等的分析,了解平面向量的实际背景,理解平面向量的意义和两个向量相等的含义.
(2)理解平面向量的几何表示和基本要素.
新知初探·自主学习——突出基础性
教材要点
知识点一 向量的概念
既有________,又有________的量称为向量.
知识点二 向量的几何表示
1.向量的表示方法
2.向量的长度(模)
||(或|a|)表示向量(或a)的______,即长度(也称模).
3.与向量有关的概念
知识点三 向量的平行或共线
状元随笔 1.理解向量概念应关注三点
(1)向量是自由向量,即只有大小和方向,而无特定的位置,这样的向量可以作任意平移.
(2)判断一个量是否为向量,就要看它是否具备了大小和方向两个因素.
(3)向量与向量之间不能比较大小.
2.相等向量的理解
任意两个相等的非零向量,都可以用同一条有向线段来表示,并且与有向线段的起点无关.在平面上,两个长度相等且指向一致的有向线段表示同一个向量,因为向量完全由它的方向和模确定.
3.共线向量与平行向量
(1)平行向量也称为共线向量,两个概念没有区别.
(2)共线向量所在直线可以平行,与平面几何中的共线不同.
(3)平行向量可以共线,与平面几何中的直线平行不同.
基础自测
1.(多选)已知向量a如图所示,下列说法正确的是( )
A.也可以用表示 B.方向是由M指向N
C.起点是M D.终点是M
2.如图,在矩形ABCD中,可以用同一条有向线段表示的向量是( )
A.和B.和
C.和D.和
3.如图,以1cm×3cm方格纸中的格点为始点和终点的所有向量中,以A为始点,可以写出________个不同的向量.
4.如图所示,在正△ABC中,D,E,F均为所在边的中点,则以下向量中与相等的是( )
A.B.
C.D.
课堂探究·素养提升——强化创新性
题型1 向量的概念、零向量、单位向量[经典例题]
例1 (1)下列物理量:①质量;②速度;③位移;④力;⑤加速度;⑥路程;⑦密度.其中不是向量的有( )
A.1个 B.2个
C.3个 D.4个
(2)给出下列说法:
①零向量是没有方向的;②零向量的长度为0;③零向量的方向是任意的;④单位向量的模都相等,其中正确的是________(填上序号).
状元随笔 (1)既有大小又有方向的量是向量.
(2)长度为0的向量是零向量.长度为1的向量是单位向量.零向量的方向是任意的.
方法归纳
判断一个量是否为向量关键看它是否具备向量的两要素:(1)有大小;(2)有方向.两个条件缺一不可.
跟踪训练1 (1)下列说法中正确的是( )
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的向量可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
(2)设a0,b0分别是a,b方向上的单位向量,则下列结论中正确的是________(填序号).
①a0=b0;②a0=-b0;③|a0|+|b0|=2;④a0∥b0.
状元随笔 结合向量的定义,由相等向量、共线向量的定义作出判断.
题型2 向量的表示[经典例题]
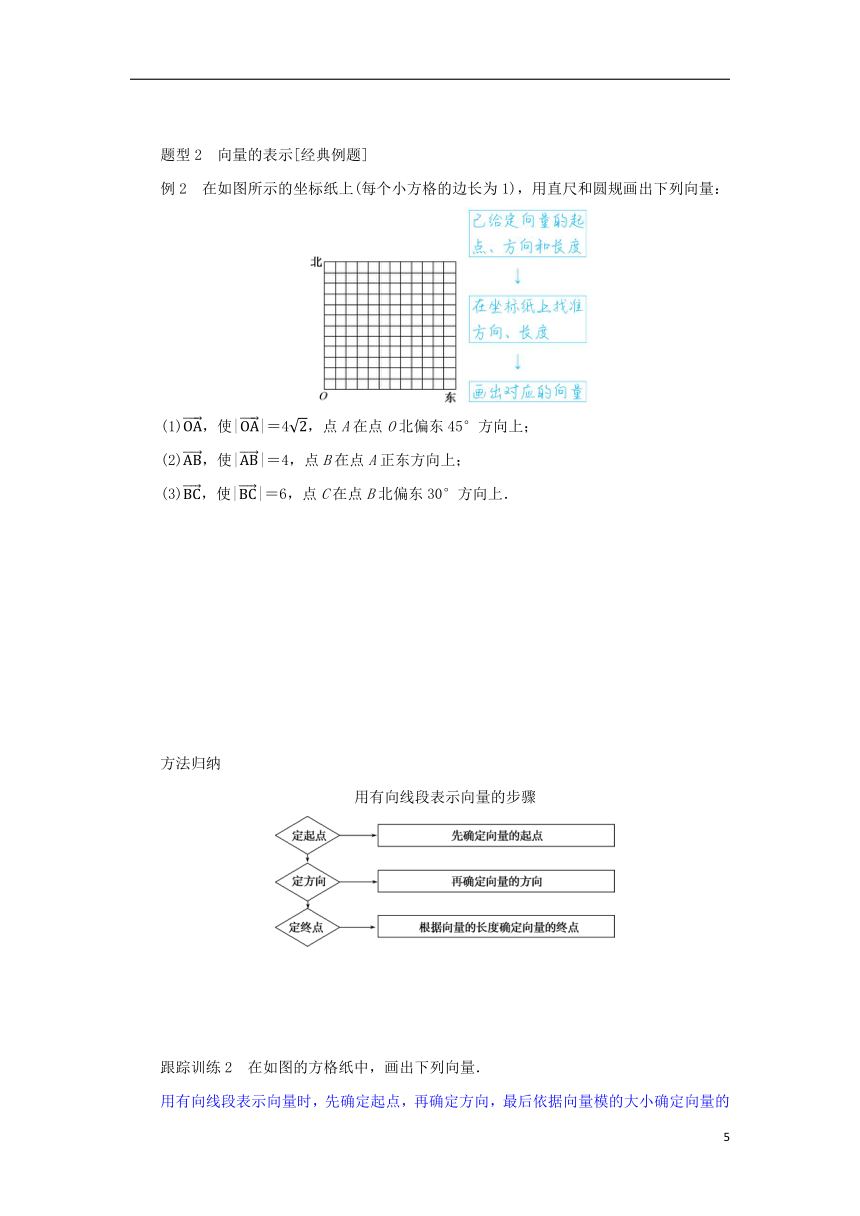
例2 在如图所示的坐标纸上(每个小方格的边长为1),用直尺和圆规画出下列向量:
(1),使||=4,点A在点O北偏东45°方向上;
(2),使||=4,点B在点A正东方向上;
(3),使||=6,点C在点B北偏东30°方向上.
方法归纳
用有向线段表示向量的步骤
跟踪训练2 在如图的方格纸中,画出下列向量.
用有向线段表示向量时,先确定起点,再确定方向,最后依据向量模的大小确定向量的终点.必要时,需依据直角三角形的知识确定出向量的方向或长度,选择合适的比例关系作出向量.
(1)||=3,点A在点O的正西方向;
(2)||=3,点B在点O北偏西45°方向;
(3)求出||的值.
题型3 共线向量与相等向量[经典例题]
例3 (1)在等腰梯形ABCD中,AB∥CD,对角线AC与BD相交于点O,EF是过点O且平行于AB的线段,在所标的向量中:
①写出与共线的向量;
②写出与方向相同的向量;
③写出与的模相等的向量;
④写出与相等的向量.
(2)判断下列命题:
①两个有共同起点而且相等的非零向量,其终点必相同;
②若a∥b,则a与b的方向相同或相反;
③若a∥b且b∥c,则a∥c;
④若a=b,则2a>b.其中正确的命题个数为( )
A.0 B.1 C.2 D.3
状元随笔 相等向量必须满足两个条件:方向相同,长度相等,相反向量方向相反,长度相等,与起始点的位置无关,所以只需在图中找与平行或共线且长度相等的所有线段,将它们表示成向量.
方法归纳
相等向量与共线向量的判断
(1)如果两个向量所在的直线平行或重合,那么这两个向量是共线向量.
(2)共线向量不一定是相等向量,但相等向量一定是共线向量.
(3)非零向量共线具有传递性,即向量a,b,c为非零向量,若a∥b,b∥c,则可推出a∥c.
注意:对于共线向量所在直线的位置关系的判断,要注意直线平行或重合两种情况.
跟踪训练3 (1)如图所示,△ABC中,三边长均不相等,E,F,D分别是AC,AB,BC的中点.
①写出与共线的向量;
②写出与长度相等的向量;
③写出与相等的向量.
状元随笔 ①共线向量只需在图中找出与线段EF平行或共线的所有线段,再把它们表示成向量即可;
②在图中找出与线段EF长度相等的所有线段,再把它们表示成向量即可;
③相等向量既要方向相同,又要大小相等.
(2)给出下列命题:
①两个向量,当且仅当它们的起点相同,终点相同时才相等;
②若平面上所有单位向量的起点移到同一个点,则其终点在同一个圆上;
③在菱形ABCD中,一定有=;
④若a=b,b=c,则a=c.
其中所有正确命题的序号为________.
6.1 平面向量及其线性运算
6.1.1 向量的概念
新知初探·自主学习
知识点一
大小 方向
知识点二
1.方向 起点 终点 向量
2.大小
3.始点和终点相同 1个 长度相等 方向相同
知识点三
相同或相反 非零 a∥b 任一向量
[基础自测]
1.解析:终点是N而不是M.
答案:ABC
2.解析:易知=.
答案:B
3.解析:由图可知,以A为始点的向量有、、、、、、,共有7个.
答案:7
4.解析:因为DE是△ABC的中位线,所以DE∥CB且DE=CB,
则与向量相等的有.
答案:D
课堂探究·素养提升
例1 【解析】 (1)②③④⑤既有大小,又有方向,是向量;
①⑥⑦只有大小,没有方向,不是向量.
(2)由零向量的方向是任意的,知①错误,③正确;由零向量的定义知②正确;由单位向量的模是1,知④正确.
【答案】 (1)C (2)②③④
跟踪训练1 解析:(1)不管向量的方向如何,它们都不能比较大小,故A,B不正确;向量的大小即为向量的模,指的是有向线段的长度,与方向无关,故C不正确;向量的模是一个数量,可以比较大小.故D正确.
(2)因为a0,b0是单位向量,|a0|=1,|b0|=1,所以|a0|+|b0|=2.
答案:(1)D (2)③
例2 【解析】
(1)由于点A在点O北偏东45°方向上,所以在坐标纸上点A距点O的横向小方格数与纵向小方格数相等.又||=4,小方格的边长为1,所以点A距点O的横向小方格数与纵向小方格数都为4,于是点A的位置可以确定,画出向量,如图所示.
(2)由于点B在点A正东方向上,且||=4,所以在坐标纸上点B距点A的横向小方格数为4,纵向小方格数为0,于是点B的位置可以确定,画出向量,如图所示.
(3)由于点C在点B北偏东30°方向上,且||=6,依据勾股定理可得,在坐标纸上点C距点B的横向小方格数为3,纵向小方格数为3≈5.2,于是点C的位置可以确定,画出向量,如图所示.
跟踪训练2 解析:取每个方格的单位长为1,
依题意,结合向量的表示可知,
(1)(2)的向量如图所示.
(3)由图知,△AOB是等腰直角三角形,
所以||==3.
例3 【解析】 (1)等腰梯形ABCD中,AB∥CD∥EF,AD=BC.
①题图中与共线的向量有.
②题图中与方向相同的向量有.
③题图中与的模相等的向量为,与的模相等的向量为.
④题图中与相等的向量为.
(2)①,两个有共同起点而且相等的非零向量,其终点必相同,根据相等向量的知识可知①是正确的.②,若a∥b,则可能b为零向量,方向任意,所以②错误.
③,若a∥b且b∥c,则可能b为零向量,此时a,c不一定平行,所以③错误.
④,向量既有长度又有方向,所以向量不能比较大小,所以④错误.故正确的命题有1个.
【答案】 (1)见解析 (2)B
跟踪训练3 解析:(1)①∵E,F分别是AC,AB的中点,∴EF∥BC,
∴与共线的向量为.
②∵E,F,D分别是AC,AB,BC的中点,
∴EF=BC,BD=DC=BC,
∴EF=BD=DC.
∵AB,BC,AC均不相等,
∴与长度相等的向量为.
③与相等的向量为.
(2)两个向量相等只要模相等且方向相同即可,而与起点和终点的位置无关,故①不正确.
单位向量的长度为1,当所有单位向量的起点在同一点O时,终点都在以O为圆心,1为半径的圆上,故②正确.
③④显然正确,故所有正确命题的序号为②③④.
答案:(1)见解析 (2)②③④
1
6.1.1 向量的概念
【课程标准】
(1)通过对力、速度、位移等的分析,了解平面向量的实际背景,理解平面向量的意义和两个向量相等的含义.
(2)理解平面向量的几何表示和基本要素.
新知初探·自主学习——突出基础性
教材要点
知识点一 向量的概念
既有________,又有________的量称为向量.
知识点二 向量的几何表示
1.向量的表示方法
2.向量的长度(模)
||(或|a|)表示向量(或a)的______,即长度(也称模).
3.与向量有关的概念
知识点三 向量的平行或共线
状元随笔 1.理解向量概念应关注三点
(1)向量是自由向量,即只有大小和方向,而无特定的位置,这样的向量可以作任意平移.
(2)判断一个量是否为向量,就要看它是否具备了大小和方向两个因素.
(3)向量与向量之间不能比较大小.
2.相等向量的理解
任意两个相等的非零向量,都可以用同一条有向线段来表示,并且与有向线段的起点无关.在平面上,两个长度相等且指向一致的有向线段表示同一个向量,因为向量完全由它的方向和模确定.
3.共线向量与平行向量
(1)平行向量也称为共线向量,两个概念没有区别.
(2)共线向量所在直线可以平行,与平面几何中的共线不同.
(3)平行向量可以共线,与平面几何中的直线平行不同.
基础自测
1.(多选)已知向量a如图所示,下列说法正确的是( )
A.也可以用表示 B.方向是由M指向N
C.起点是M D.终点是M
2.如图,在矩形ABCD中,可以用同一条有向线段表示的向量是( )
A.和B.和
C.和D.和
3.如图,以1cm×3cm方格纸中的格点为始点和终点的所有向量中,以A为始点,可以写出________个不同的向量.
4.如图所示,在正△ABC中,D,E,F均为所在边的中点,则以下向量中与相等的是( )
A.B.
C.D.
课堂探究·素养提升——强化创新性
题型1 向量的概念、零向量、单位向量[经典例题]
例1 (1)下列物理量:①质量;②速度;③位移;④力;⑤加速度;⑥路程;⑦密度.其中不是向量的有( )
A.1个 B.2个
C.3个 D.4个
(2)给出下列说法:
①零向量是没有方向的;②零向量的长度为0;③零向量的方向是任意的;④单位向量的模都相等,其中正确的是________(填上序号).
状元随笔 (1)既有大小又有方向的量是向量.
(2)长度为0的向量是零向量.长度为1的向量是单位向量.零向量的方向是任意的.
方法归纳
判断一个量是否为向量关键看它是否具备向量的两要素:(1)有大小;(2)有方向.两个条件缺一不可.
跟踪训练1 (1)下列说法中正确的是( )
A.数量可以比较大小,向量也可以比较大小
B.方向不同的向量不能比较大小,但同向的向量可以比较大小
C.向量的大小与方向有关
D.向量的模可以比较大小
(2)设a0,b0分别是a,b方向上的单位向量,则下列结论中正确的是________(填序号).
①a0=b0;②a0=-b0;③|a0|+|b0|=2;④a0∥b0.
状元随笔 结合向量的定义,由相等向量、共线向量的定义作出判断.
题型2 向量的表示[经典例题]
例2 在如图所示的坐标纸上(每个小方格的边长为1),用直尺和圆规画出下列向量:
(1),使||=4,点A在点O北偏东45°方向上;
(2),使||=4,点B在点A正东方向上;
(3),使||=6,点C在点B北偏东30°方向上.
方法归纳
用有向线段表示向量的步骤
跟踪训练2 在如图的方格纸中,画出下列向量.
用有向线段表示向量时,先确定起点,再确定方向,最后依据向量模的大小确定向量的终点.必要时,需依据直角三角形的知识确定出向量的方向或长度,选择合适的比例关系作出向量.
(1)||=3,点A在点O的正西方向;
(2)||=3,点B在点O北偏西45°方向;
(3)求出||的值.
题型3 共线向量与相等向量[经典例题]
例3 (1)在等腰梯形ABCD中,AB∥CD,对角线AC与BD相交于点O,EF是过点O且平行于AB的线段,在所标的向量中:
①写出与共线的向量;
②写出与方向相同的向量;
③写出与的模相等的向量;
④写出与相等的向量.
(2)判断下列命题:
①两个有共同起点而且相等的非零向量,其终点必相同;
②若a∥b,则a与b的方向相同或相反;
③若a∥b且b∥c,则a∥c;
④若a=b,则2a>b.其中正确的命题个数为( )
A.0 B.1 C.2 D.3
状元随笔 相等向量必须满足两个条件:方向相同,长度相等,相反向量方向相反,长度相等,与起始点的位置无关,所以只需在图中找与平行或共线且长度相等的所有线段,将它们表示成向量.
方法归纳
相等向量与共线向量的判断
(1)如果两个向量所在的直线平行或重合,那么这两个向量是共线向量.
(2)共线向量不一定是相等向量,但相等向量一定是共线向量.
(3)非零向量共线具有传递性,即向量a,b,c为非零向量,若a∥b,b∥c,则可推出a∥c.
注意:对于共线向量所在直线的位置关系的判断,要注意直线平行或重合两种情况.
跟踪训练3 (1)如图所示,△ABC中,三边长均不相等,E,F,D分别是AC,AB,BC的中点.
①写出与共线的向量;
②写出与长度相等的向量;
③写出与相等的向量.
状元随笔 ①共线向量只需在图中找出与线段EF平行或共线的所有线段,再把它们表示成向量即可;
②在图中找出与线段EF长度相等的所有线段,再把它们表示成向量即可;
③相等向量既要方向相同,又要大小相等.
(2)给出下列命题:
①两个向量,当且仅当它们的起点相同,终点相同时才相等;
②若平面上所有单位向量的起点移到同一个点,则其终点在同一个圆上;
③在菱形ABCD中,一定有=;
④若a=b,b=c,则a=c.
其中所有正确命题的序号为________.
6.1 平面向量及其线性运算
6.1.1 向量的概念
新知初探·自主学习
知识点一
大小 方向
知识点二
1.方向 起点 终点 向量
2.大小
3.始点和终点相同 1个 长度相等 方向相同
知识点三
相同或相反 非零 a∥b 任一向量
[基础自测]
1.解析:终点是N而不是M.
答案:ABC
2.解析:易知=.
答案:B
3.解析:由图可知,以A为始点的向量有、、、、、、,共有7个.
答案:7
4.解析:因为DE是△ABC的中位线,所以DE∥CB且DE=CB,
则与向量相等的有.
答案:D
课堂探究·素养提升
例1 【解析】 (1)②③④⑤既有大小,又有方向,是向量;
①⑥⑦只有大小,没有方向,不是向量.
(2)由零向量的方向是任意的,知①错误,③正确;由零向量的定义知②正确;由单位向量的模是1,知④正确.
【答案】 (1)C (2)②③④
跟踪训练1 解析:(1)不管向量的方向如何,它们都不能比较大小,故A,B不正确;向量的大小即为向量的模,指的是有向线段的长度,与方向无关,故C不正确;向量的模是一个数量,可以比较大小.故D正确.
(2)因为a0,b0是单位向量,|a0|=1,|b0|=1,所以|a0|+|b0|=2.
答案:(1)D (2)③
例2 【解析】
(1)由于点A在点O北偏东45°方向上,所以在坐标纸上点A距点O的横向小方格数与纵向小方格数相等.又||=4,小方格的边长为1,所以点A距点O的横向小方格数与纵向小方格数都为4,于是点A的位置可以确定,画出向量,如图所示.
(2)由于点B在点A正东方向上,且||=4,所以在坐标纸上点B距点A的横向小方格数为4,纵向小方格数为0,于是点B的位置可以确定,画出向量,如图所示.
(3)由于点C在点B北偏东30°方向上,且||=6,依据勾股定理可得,在坐标纸上点C距点B的横向小方格数为3,纵向小方格数为3≈5.2,于是点C的位置可以确定,画出向量,如图所示.
跟踪训练2 解析:取每个方格的单位长为1,
依题意,结合向量的表示可知,
(1)(2)的向量如图所示.
(3)由图知,△AOB是等腰直角三角形,
所以||==3.
例3 【解析】 (1)等腰梯形ABCD中,AB∥CD∥EF,AD=BC.
①题图中与共线的向量有.
②题图中与方向相同的向量有.
③题图中与的模相等的向量为,与的模相等的向量为.
④题图中与相等的向量为.
(2)①,两个有共同起点而且相等的非零向量,其终点必相同,根据相等向量的知识可知①是正确的.②,若a∥b,则可能b为零向量,方向任意,所以②错误.
③,若a∥b且b∥c,则可能b为零向量,此时a,c不一定平行,所以③错误.
④,向量既有长度又有方向,所以向量不能比较大小,所以④错误.故正确的命题有1个.
【答案】 (1)见解析 (2)B
跟踪训练3 解析:(1)①∵E,F分别是AC,AB的中点,∴EF∥BC,
∴与共线的向量为.
②∵E,F,D分别是AC,AB,BC的中点,
∴EF=BC,BD=DC=BC,
∴EF=BD=DC.
∵AB,BC,AC均不相等,
∴与长度相等的向量为.
③与相等的向量为.
(2)两个向量相等只要模相等且方向相同即可,而与起点和终点的位置无关,故①不正确.
单位向量的长度为1,当所有单位向量的起点在同一点O时,终点都在以O为圆心,1为半径的圆上,故②正确.
③④显然正确,故所有正确命题的序号为②③④.
答案:(1)见解析 (2)②③④
1
