新人教B版必修第二册5.1.4用样本估计总体学案
文档属性
| 名称 | 新人教B版必修第二册5.1.4用样本估计总体学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 207.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览



文档简介
5.1.4 用样本估计总体
【课程标准】
①结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数),理解集中趋势参数的统计含义.②结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义.③结合实例,能用样本估计总体的取值规律.
新知初探·自主学习——突出基础性
教材要点
知识点一 用样本估计总体
(1)前提:样本的容量恰当,抽样方法合理.
(2)必要性
①在容许一定________存在的前提下,可以用样本估计总体,这样能节省人力和物力.
②有时候总体的________不可能获得,只能用样本估计总体.
(3)误差:估计一般是有误差的.但是,________可以保证,当样本的容量越来越大时,估计的误差很小的可能性将越来越大.
状元随笔 用样本估计总体出现误差的原因有哪些?
提示:样本抽取的随机性;样本抽取的方法不合适,导致代表性差;样本容量偏少等.
知识点二 用样本的数字特征估计总体的数字特征
一般情况下,如果样本的容量恰当,抽样方法又合理的话,样本的特征能够反映总体的特征.特别地,样本平均数(也称为样本均值)、方差(也称为样本方差)与总体对应的值相差不会太大.
状元随笔 用样本的数字特征来描述总体的数字特征时,通常从哪两个方面分析?
提示:(1)分析数据的集中趋势或取值的平均水平,如平均数、众数、中位数、百分位数;
(2)分析数据的离散程度或围绕平均数波动的大小,如极差、方差和标准差.标准差、方差越大,数据离散程度越大,越不稳定;标准差、方差越小,数据的离散程度越小,越稳定.
知识点三 分层抽样下用样本的数字特征估计总
体的数字特征
假设第一层有m个数,分别为x1,x2,…,xm,平均数为,方差为s2;第二层有n个数,分别为y1,y2,…,yn,平均数为,方差为t2,则
=,s2=
=,t2=
如果记样本均值为,样本方差为b2,则可以计算出
==
b2=
=
知识点四 用样本的分布估计总体的分布
同数字特征的估计一样,分布的估计一般也有误差.如果总体在每一个分组的频率记为:π1,π2,…,πn,样本在每一组对应的频率记为p1,p2,…,pn,一般来说,
= [(π1-p1)2+(π2-p2)2+…(πn-pn)2] 不等于0,同样,大数定律可以保证,当样本的容量越来越大时,上式很小的可能性越来越大.
基础自测
1.下列说法不正确的是( )
A.频率分布直方图中每个小矩形的高就是该组的频率
B.频率分布直方图中各个小矩形的面积之和等于1
C.频率分布直方图中各个小矩形的宽一样大
D.频率分布折线图是依次连接频率分布直方图的每个小矩形上边的中点得到的
2.如图,这是某校高三年级甲、乙两班在上学期的5次数学测试的班级平均分的茎叶图,则下列说法不正确的是( )
A.甲班的数学成绩平均分的平均水平高于乙班
B.甲班的数学成绩的平均分比乙班稳定
C.甲班的数学成绩平均分的中位数高于乙班
D.甲、乙两班这5次数学测试的总平均分是103
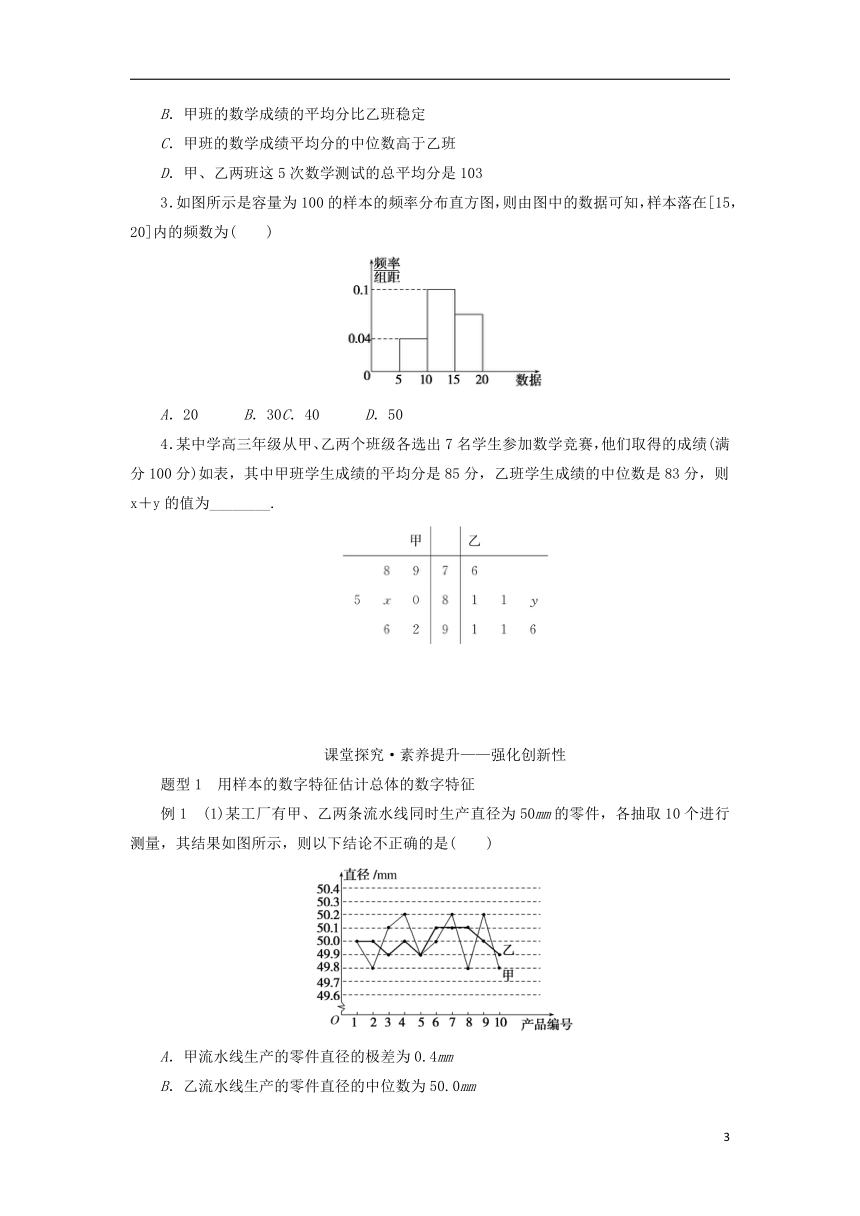
3.如图所示是容量为100的样本的频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )
A.20 B.30C.40 D.50
4.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)如表,其中甲班学生成绩的平均分是85分,乙班学生成绩的中位数是83分,则x+y的值为________.
课堂探究·素养提升——强化创新性
题型1 用样本的数字特征估计总体的数字特征
例1 (1)某工厂有甲、乙两条流水线同时生产直径为50mm的零件,各抽取10个进行测量,其结果如图所示,则以下结论不正确的是( )
A.甲流水线生产的零件直径的极差为0.4mm
B.乙流水线生产的零件直径的中位数为50.0mm
C.乙流水线生产的零件直径比甲流水线生产的零件直径稳定
D.甲流水线生产的零件直径的平均值小于乙流水线生产的零件直径的平均值
(2)下表是某超市5月份一周的利润情况记录:
日期 12日 13日 14日 15日 16日 17日 18日
当日利 润/万元 0.20 0.17 0.23 0.21 0.23 0.18 0.25
根据上表你估计该超市今年五月份的总利润是( )
A.6.51万元 B.6.4万元
C.1.47万元 D.5.88万元
(3)为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的正确的统计结论的编号为( )
A.①③ B.①④C.②③ D.②④
方法归纳
(1)用样本的数字特征估计总体的数字特征的可行性
①如果抽样的方法比较合理,那么样本可以反映总体的信息,但从样本得到的信息会有偏差,这些偏差是由样本的随机性引起的.
②虽然样本的数字特征并不是总体真正的数字特征,而是总体的一个估计,但这种估计是合理的,特别是当样本容量很大时,样本的数字特征稳定于总体的数字特征.
(2)样本数字特征所反映的样本的特征
一般地,平均数反映的是样本个体的平均水平,众数和中位数则反映样本中个体的“重心”,而标准差则反映了样本的波动程度、离散程度,即均衡性、稳定性、差异性等.因此,我们可以根据问题的需要选择用样本的不同数字特征来分析问题.
跟踪训练1 (1)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A. B. C.3 D.
(2)林管部门在每年3月12日植树节前,为保证树苗的质量,都会对树苗进行检测,现从甲乙两种树苗中抽测了10株树苗的高度,其茎叶图如图,下列描述正确的是( )
A.甲种树苗的平均高度大于乙种树苗的平均高度,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的平均高度大于乙种树苗的平均高度,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的平均高度大于甲种树苗的平均高度,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的平均高度大于甲种树苗的平均高度,但甲种树苗比乙种树苗长得整齐
题型2 用样本的分布估计总体的分布[数据分析]
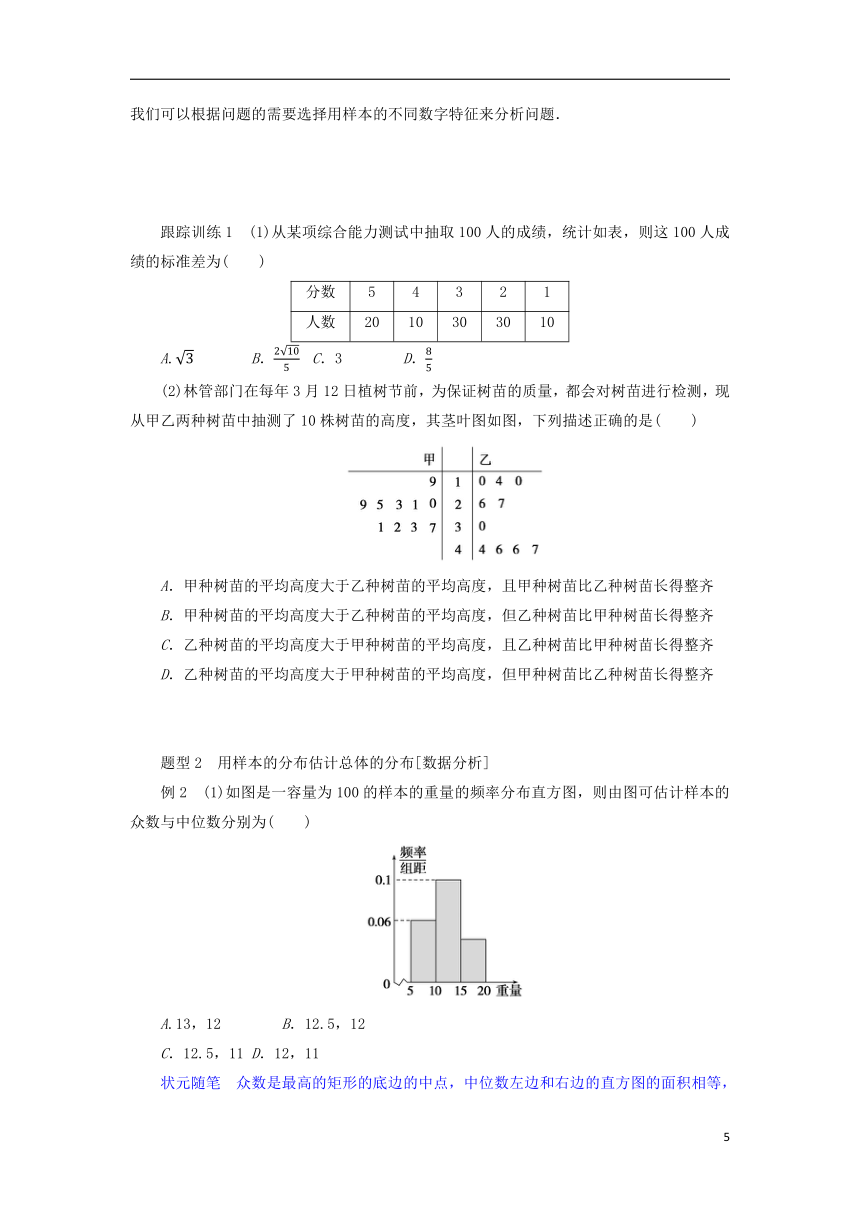
例2 (1)如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本的众数与中位数分别为( )
A.13,12 B.12.5,12
C.12.5,11 D.12,11
状元随笔 众数是最高的矩形的底边的中点,中位数左边和右边的直方图的面积相等,都是0.5.
(2)2021年起,我省实行“3+1+2”高考模式,某中学为了解本校学生的选考情况,随机调查了100位学生,其中选考化学或生物的学生共有70位,选考化学的学生共有40位,选考化学且选考生物的学生共有20位.若该校共有1500位学生,则该校选考生物的学生人数估计值为( )
A.300B.450
C.600D.750
方法归纳
总体的分布分两种情况
(1)当总体中的个体取值很少时,用茎叶图估计总体的分布;
(2)当总体中的个体取值较多时,将样本数据恰当分组,用各组的频率分布描述总体的分布,方法是用频率分布表或频率分布直方图.
跟踪训练2 某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y [-0.20,0) [0,0.20) [0.20,0.40) [0.40,0.60) [0.60,0.80)
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
附:≈8.602.
状元随笔 (1)用样本中[0.40,0.60)和[0.60,0.80)内的比例估计产值增长率不低于40%的企业比例,[-0.20,0)内的比例估计产值负增长的企业比例;
(2)根据公式求平均数.
题型3 频率分布直方图与数字特征的综合应用[直观想象、数学运算]
例3 已知一组数据:
125121123125127129125128130129
126124125127126122124125126128
(1)填写下面的频率分布表:
分组 频数累计 频数 频率
[120.5,122.5)
[122.5,124.5)
[124.5,126.5)
[126.5,128.5)
[128.5,130.5]
合计
(2)作出频率分布直方图;
(3)根据频率分布直方图或频率分布表求这组数据的众数、中位数和平均数.
状元随笔 (1)将所给数据按从小到大的顺序排序,列表.
(2)根据频率分布表作出频率分布直方图.
(3)根据频率分布表(直方图)计算这组数据的众数、中位数和平均数.
方法归纳
(1)利用频率分布直方图求数字特征:
①众数是最高的矩形的底边的中点;
②中位数左右两侧直方图的面积相等;
③平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和.
(2)利用直方图求众数、中位数、平均数均为近似值,往往与实际数据得出的不一致,但它们能粗略估计其众数、中位数和平均数.
跟踪训练3 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
5.1.4 用样本估计总体
新知初探·自主学习
知识点一
误差 数字特征 大数定律
[基础自测]
1.解析:频率分布直方图中每个小矩形的高=.
答案:A
2.解析:由题意可得甲班的平均分的平均值是104,中位数是103,方差是26.4;
乙班的平均分的平均值是102,中位数是101,方差是37.6,则A,B,C正确,不符合题意.
因为甲、乙两班的人数不知道,所以两班的总平均分无法计算,故D错误,符合题意.
答案:D
3.解析:样本数据落在[15,20]内的频数为100×[1-5×(0.04+0.1)]=30.
答案:B
4.解析:因为甲班学生成绩的平均分是85,所以=85,解得x=5,又因为乙班学生成绩的中位数是83,所以y=3,所以x+y=8.
答案:8
课堂探究·素养提升
例1 【解析】 (1)对A,甲流水线生产的零件直径的极差为50.2-49.8=0.4(mm).故A正确,不符合题意.
对B,易得除去3个50.1与3个49.9,剩下的均为50.0.故中位数为50.0mm.故B正确,不符合题意.
对C,由图表易得,乙流水线生产的零件直径比甲流水线生产的零件直径稳定.故C正确,不符合题意.
对D,计算可得甲、乙流水线生产的零件直径平均值均为50.0mm.故D错误,符合题意.
(2)从表中一周的利润可得一天的平均利润为
==0.21.
又五月份共有31天,
所以五月份的总利润约是0.21×31=6.51(万元).
(3)方法一 因为==29,
==30,
所以<,
又==,
==2,
所以s甲>s乙.故可判断结论①④正确.
方法二 甲地该月14时的气温数据分布在26℃和31℃之间,且数据波动较大,而乙地该月14时的气温数据分布在28℃和32℃之间,且数据波动较小,可以判断结论①④正确.
【答案】 (1)D (2)A (3)B
跟踪训练1 解析:(1)因为==3,
所以s2=[(x1-)2+(x2-)2+…+(xn-)2]
=(20×22+10×12+30×12+10×22)==,
所以s=.
(2)由茎叶图中的数据,我们可得甲、乙两种树苗抽取的样本高度分别为:
甲:19,20,21,23,25,29,31,32,33,37
乙:10,10,14,26,27,30,44,46,46,47
由已知易得:
=(19+20+21+23+25+29+31+32+33+37)÷10=27,
=(10+10+14+26+27+30+44+46+46+47)÷10=30,
故乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐.
答案:(1)B (2)D
例2 【解析】 (1)观察频率分布直方图可知众数为=12.5,设中位数为x,
则0.06×5+(x-10)×0.1=0.5,
解得x=12
(2)因为选考化学或生物的学生共有70位,选考化学的学生共有40位,
所以选考生物没有选考化学的学生共有70-40=30位,
又选考化学且选考生物的学生共有20位,
所以选考生物的学生有30+20=50位,
所以在100位学生中选考生物的占比为,
该校共有1500位学生,则该校选考生物的学生人数的估计值为×1500=750人.
【答案】 (1)B (2)D
跟踪训练2 解析:(1)根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于40%的企业频率为=0.21.
产值负增长的企业频率为=0.02.
用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%,产值负增长的企业比例为2%.
(2)=(-0.10×2+0.10×24+0.30×53+0.50×14+0.70×7)=0.30,
s2=(yi-)2=[(-0.40)2×2+(-0.20)2×24+02×53+0.202×14+0.402×7]=0.0296,
所以s==0.02×≈0.17,
所以,这类企业产值增长率的平均数与标准差的估计值分别为30%,0.17.
例3 【解析】 (1)频率分布表如表:
分组 频数累计 频数 频率
[120.5,122.5) 2 0.1
[122.5,124.5) 3 0.15
[124.5,126.5) 正 8 0.4
[126.5,128.5) 4 0.2
[128.5,130.5] 3 0.15
合计 20 1
(2)
(3)在[124.5,126.5)中的数据最多,取这个区间的中点值作为众数的近似值,得众数为125.5,事实上,众数的精确值为125.图中虚线对应的数据是124.5+2×=125.75,事实上,中位数为125.5.使用“组中值”求平均数:=121.5×0.1+123.5×0.15+125.5×0.4+127.5×0.2+129.5×0.15=125.8,事实上,平均数的精确值为=125.75.
跟踪训练3 解析:(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:x=0.0075,所以直方图中x的值是0.0075.
(2)月平均用电量的众数是=230.
因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5得a=224,所以月平均用电量的中位数是224.
(3)月平均用电量在[220,240)的用户有0.0125×20×100=25(户),
月平均用电量在[240,260)的用户有0.0075×20×100=15(户),月平均用电量在[260,280)的用户有0.005×20×100=10(户),月平均用电量在[280,300]的用户有0.0025×20×100=5(户),
抽取比例==,所以月平均用电量在[220,240)的用户中应抽取25×=5(户).
2
【课程标准】
①结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数),理解集中趋势参数的统计含义.②结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义.③结合实例,能用样本估计总体的取值规律.
新知初探·自主学习——突出基础性
教材要点
知识点一 用样本估计总体
(1)前提:样本的容量恰当,抽样方法合理.
(2)必要性
①在容许一定________存在的前提下,可以用样本估计总体,这样能节省人力和物力.
②有时候总体的________不可能获得,只能用样本估计总体.
(3)误差:估计一般是有误差的.但是,________可以保证,当样本的容量越来越大时,估计的误差很小的可能性将越来越大.
状元随笔 用样本估计总体出现误差的原因有哪些?
提示:样本抽取的随机性;样本抽取的方法不合适,导致代表性差;样本容量偏少等.
知识点二 用样本的数字特征估计总体的数字特征
一般情况下,如果样本的容量恰当,抽样方法又合理的话,样本的特征能够反映总体的特征.特别地,样本平均数(也称为样本均值)、方差(也称为样本方差)与总体对应的值相差不会太大.
状元随笔 用样本的数字特征来描述总体的数字特征时,通常从哪两个方面分析?
提示:(1)分析数据的集中趋势或取值的平均水平,如平均数、众数、中位数、百分位数;
(2)分析数据的离散程度或围绕平均数波动的大小,如极差、方差和标准差.标准差、方差越大,数据离散程度越大,越不稳定;标准差、方差越小,数据的离散程度越小,越稳定.
知识点三 分层抽样下用样本的数字特征估计总
体的数字特征
假设第一层有m个数,分别为x1,x2,…,xm,平均数为,方差为s2;第二层有n个数,分别为y1,y2,…,yn,平均数为,方差为t2,则
=,s2=
=,t2=
如果记样本均值为,样本方差为b2,则可以计算出
==
b2=
=
知识点四 用样本的分布估计总体的分布
同数字特征的估计一样,分布的估计一般也有误差.如果总体在每一个分组的频率记为:π1,π2,…,πn,样本在每一组对应的频率记为p1,p2,…,pn,一般来说,
= [(π1-p1)2+(π2-p2)2+…(πn-pn)2] 不等于0,同样,大数定律可以保证,当样本的容量越来越大时,上式很小的可能性越来越大.
基础自测
1.下列说法不正确的是( )
A.频率分布直方图中每个小矩形的高就是该组的频率
B.频率分布直方图中各个小矩形的面积之和等于1
C.频率分布直方图中各个小矩形的宽一样大
D.频率分布折线图是依次连接频率分布直方图的每个小矩形上边的中点得到的
2.如图,这是某校高三年级甲、乙两班在上学期的5次数学测试的班级平均分的茎叶图,则下列说法不正确的是( )
A.甲班的数学成绩平均分的平均水平高于乙班
B.甲班的数学成绩的平均分比乙班稳定
C.甲班的数学成绩平均分的中位数高于乙班
D.甲、乙两班这5次数学测试的总平均分是103
3.如图所示是容量为100的样本的频率分布直方图,则由图中的数据可知,样本落在[15,20]内的频数为( )
A.20 B.30C.40 D.50
4.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)如表,其中甲班学生成绩的平均分是85分,乙班学生成绩的中位数是83分,则x+y的值为________.
课堂探究·素养提升——强化创新性
题型1 用样本的数字特征估计总体的数字特征
例1 (1)某工厂有甲、乙两条流水线同时生产直径为50mm的零件,各抽取10个进行测量,其结果如图所示,则以下结论不正确的是( )
A.甲流水线生产的零件直径的极差为0.4mm
B.乙流水线生产的零件直径的中位数为50.0mm
C.乙流水线生产的零件直径比甲流水线生产的零件直径稳定
D.甲流水线生产的零件直径的平均值小于乙流水线生产的零件直径的平均值
(2)下表是某超市5月份一周的利润情况记录:
日期 12日 13日 14日 15日 16日 17日 18日
当日利 润/万元 0.20 0.17 0.23 0.21 0.23 0.18 0.25
根据上表你估计该超市今年五月份的总利润是( )
A.6.51万元 B.6.4万元
C.1.47万元 D.5.88万元
(3)为比较甲、乙两地某月14时的气温情况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的正确的统计结论的编号为( )
A.①③ B.①④C.②③ D.②④
方法归纳
(1)用样本的数字特征估计总体的数字特征的可行性
①如果抽样的方法比较合理,那么样本可以反映总体的信息,但从样本得到的信息会有偏差,这些偏差是由样本的随机性引起的.
②虽然样本的数字特征并不是总体真正的数字特征,而是总体的一个估计,但这种估计是合理的,特别是当样本容量很大时,样本的数字特征稳定于总体的数字特征.
(2)样本数字特征所反映的样本的特征
一般地,平均数反映的是样本个体的平均水平,众数和中位数则反映样本中个体的“重心”,而标准差则反映了样本的波动程度、离散程度,即均衡性、稳定性、差异性等.因此,我们可以根据问题的需要选择用样本的不同数字特征来分析问题.
跟踪训练1 (1)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
分数 5 4 3 2 1
人数 20 10 30 30 10
A. B. C.3 D.
(2)林管部门在每年3月12日植树节前,为保证树苗的质量,都会对树苗进行检测,现从甲乙两种树苗中抽测了10株树苗的高度,其茎叶图如图,下列描述正确的是( )
A.甲种树苗的平均高度大于乙种树苗的平均高度,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的平均高度大于乙种树苗的平均高度,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的平均高度大于甲种树苗的平均高度,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的平均高度大于甲种树苗的平均高度,但甲种树苗比乙种树苗长得整齐
题型2 用样本的分布估计总体的分布[数据分析]
例2 (1)如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本的众数与中位数分别为( )
A.13,12 B.12.5,12
C.12.5,11 D.12,11
状元随笔 众数是最高的矩形的底边的中点,中位数左边和右边的直方图的面积相等,都是0.5.
(2)2021年起,我省实行“3+1+2”高考模式,某中学为了解本校学生的选考情况,随机调查了100位学生,其中选考化学或生物的学生共有70位,选考化学的学生共有40位,选考化学且选考生物的学生共有20位.若该校共有1500位学生,则该校选考生物的学生人数估计值为( )
A.300B.450
C.600D.750
方法归纳
总体的分布分两种情况
(1)当总体中的个体取值很少时,用茎叶图估计总体的分布;
(2)当总体中的个体取值较多时,将样本数据恰当分组,用各组的频率分布描述总体的分布,方法是用频率分布表或频率分布直方图.
跟踪训练2 某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
y [-0.20,0) [0,0.20) [0.20,0.40) [0.40,0.60) [0.60,0.80)
企业数 2 24 53 14 7
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
附:≈8.602.
状元随笔 (1)用样本中[0.40,0.60)和[0.60,0.80)内的比例估计产值增长率不低于40%的企业比例,[-0.20,0)内的比例估计产值负增长的企业比例;
(2)根据公式求平均数.
题型3 频率分布直方图与数字特征的综合应用[直观想象、数学运算]
例3 已知一组数据:
125121123125127129125128130129
126124125127126122124125126128
(1)填写下面的频率分布表:
分组 频数累计 频数 频率
[120.5,122.5)
[122.5,124.5)
[124.5,126.5)
[126.5,128.5)
[128.5,130.5]
合计
(2)作出频率分布直方图;
(3)根据频率分布直方图或频率分布表求这组数据的众数、中位数和平均数.
状元随笔 (1)将所给数据按从小到大的顺序排序,列表.
(2)根据频率分布表作出频率分布直方图.
(3)根据频率分布表(直方图)计算这组数据的众数、中位数和平均数.
方法归纳
(1)利用频率分布直方图求数字特征:
①众数是最高的矩形的底边的中点;
②中位数左右两侧直方图的面积相等;
③平均数等于每个小矩形的面积乘以小矩形底边中点的横坐标之和.
(2)利用直方图求众数、中位数、平均数均为近似值,往往与实际数据得出的不一致,但它们能粗略估计其众数、中位数和平均数.
跟踪训练3 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
5.1.4 用样本估计总体
新知初探·自主学习
知识点一
误差 数字特征 大数定律
[基础自测]
1.解析:频率分布直方图中每个小矩形的高=.
答案:A
2.解析:由题意可得甲班的平均分的平均值是104,中位数是103,方差是26.4;
乙班的平均分的平均值是102,中位数是101,方差是37.6,则A,B,C正确,不符合题意.
因为甲、乙两班的人数不知道,所以两班的总平均分无法计算,故D错误,符合题意.
答案:D
3.解析:样本数据落在[15,20]内的频数为100×[1-5×(0.04+0.1)]=30.
答案:B
4.解析:因为甲班学生成绩的平均分是85,所以=85,解得x=5,又因为乙班学生成绩的中位数是83,所以y=3,所以x+y=8.
答案:8
课堂探究·素养提升
例1 【解析】 (1)对A,甲流水线生产的零件直径的极差为50.2-49.8=0.4(mm).故A正确,不符合题意.
对B,易得除去3个50.1与3个49.9,剩下的均为50.0.故中位数为50.0mm.故B正确,不符合题意.
对C,由图表易得,乙流水线生产的零件直径比甲流水线生产的零件直径稳定.故C正确,不符合题意.
对D,计算可得甲、乙流水线生产的零件直径平均值均为50.0mm.故D错误,符合题意.
(2)从表中一周的利润可得一天的平均利润为
==0.21.
又五月份共有31天,
所以五月份的总利润约是0.21×31=6.51(万元).
(3)方法一 因为==29,
==30,
所以<,
又==,
==2,
所以s甲>s乙.故可判断结论①④正确.
方法二 甲地该月14时的气温数据分布在26℃和31℃之间,且数据波动较大,而乙地该月14时的气温数据分布在28℃和32℃之间,且数据波动较小,可以判断结论①④正确.
【答案】 (1)D (2)A (3)B
跟踪训练1 解析:(1)因为==3,
所以s2=[(x1-)2+(x2-)2+…+(xn-)2]
=(20×22+10×12+30×12+10×22)==,
所以s=.
(2)由茎叶图中的数据,我们可得甲、乙两种树苗抽取的样本高度分别为:
甲:19,20,21,23,25,29,31,32,33,37
乙:10,10,14,26,27,30,44,46,46,47
由已知易得:
=(19+20+21+23+25+29+31+32+33+37)÷10=27,
=(10+10+14+26+27+30+44+46+46+47)÷10=30,
故乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐.
答案:(1)B (2)D
例2 【解析】 (1)观察频率分布直方图可知众数为=12.5,设中位数为x,
则0.06×5+(x-10)×0.1=0.5,
解得x=12
(2)因为选考化学或生物的学生共有70位,选考化学的学生共有40位,
所以选考生物没有选考化学的学生共有70-40=30位,
又选考化学且选考生物的学生共有20位,
所以选考生物的学生有30+20=50位,
所以在100位学生中选考生物的占比为,
该校共有1500位学生,则该校选考生物的学生人数的估计值为×1500=750人.
【答案】 (1)B (2)D
跟踪训练2 解析:(1)根据产值增长率频数分布表得,所调查的100个企业中产值增长率不低于40%的企业频率为=0.21.
产值负增长的企业频率为=0.02.
用样本频率分布估计总体分布得这类企业中产值增长率不低于40%的企业比例为21%,产值负增长的企业比例为2%.
(2)=(-0.10×2+0.10×24+0.30×53+0.50×14+0.70×7)=0.30,
s2=(yi-)2=[(-0.40)2×2+(-0.20)2×24+02×53+0.202×14+0.402×7]=0.0296,
所以s==0.02×≈0.17,
所以,这类企业产值增长率的平均数与标准差的估计值分别为30%,0.17.
例3 【解析】 (1)频率分布表如表:
分组 频数累计 频数 频率
[120.5,122.5) 2 0.1
[122.5,124.5) 3 0.15
[124.5,126.5) 正 8 0.4
[126.5,128.5) 4 0.2
[128.5,130.5] 3 0.15
合计 20 1
(2)
(3)在[124.5,126.5)中的数据最多,取这个区间的中点值作为众数的近似值,得众数为125.5,事实上,众数的精确值为125.图中虚线对应的数据是124.5+2×=125.75,事实上,中位数为125.5.使用“组中值”求平均数:=121.5×0.1+123.5×0.15+125.5×0.4+127.5×0.2+129.5×0.15=125.8,事实上,平均数的精确值为=125.75.
跟踪训练3 解析:(1)由直方图的性质可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:x=0.0075,所以直方图中x的值是0.0075.
(2)月平均用电量的众数是=230.
因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,设中位数为a,
由(0.002+0.0095+0.011)×20+0.0125×(a-220)=0.5得a=224,所以月平均用电量的中位数是224.
(3)月平均用电量在[220,240)的用户有0.0125×20×100=25(户),
月平均用电量在[240,260)的用户有0.0075×20×100=15(户),月平均用电量在[260,280)的用户有0.005×20×100=10(户),月平均用电量在[280,300]的用户有0.0025×20×100=5(户),
抽取比例==,所以月平均用电量在[220,240)的用户中应抽取25×=5(户).
2
