新人教B版必修第二册4.3指数函数与对数函数的关系学案
文档属性
| 名称 | 新人教B版必修第二册4.3指数函数与对数函数的关系学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 74.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 00:00:00 | ||
图片预览




文档简介
4.3 指数函数与对数函数的关系
【课程标准】
(1)了解反函数的定义.
(2)了解指数函数与对数函数互为反函数.
新知初探·自主学习——突出基础性
教材要点
知识点一 反函数的定义
(1)定义:如果在函数y=f(x)中,给定值域中________________,只有________与之对应,那么x是y的函数,这个函数称为y=f(x)的反函数.
(2)记法:y=f-1(x).
状元随笔 1.函数f(x)=x2有反函数吗?为什么?
提示:没有.若令y=f(x)=1,则x=±1,即x值不唯一,不符合反函数的定义.
2.什么样的函数一定有反函数?
提示:单调函数.
知识点二 反函数的求法
对调y=f(x)中的x与y,然后从x=f(y)中求出y得到.
知识点三 函数与其反函数的性质的关系
(1)图象:关于直线y=x对称;
(2)定义域、值域:原函数的________与其反函数的________相同;原函数的________与其反函数的________相同.
(3)单调性:原函数与其反函数的单调性________.
知识点四 指数函数与对数函数的性质
函数 指数函数y=ax 对数函数y=logax
定义域 ________ ________
值域 ________ ________
单调性 01时,为________
状元随笔 指数函数y=ax与对数函数y=logax,一个函数的定义域是另一个函数的值域,而且它们的单调性相同.
基础自测
1.函数f(x)=log4x与g(x)=4x的图象( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
2.若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=( )
A. B.log2x
C.x D.2x-2
3.若函数f(x)=2x的反函数为f-1(x),则f-1(1)=________.
4.若函数y=f(x)的图象位于第一、二象限,则它的反函数y=f-1(x)的图象位于( )
A.第一、二象限 B.第三、四象限
C.第二、三象限 D.第一、四象限
课堂探究·素养提升——强化创新性
题型1 判断函数是否有反函数(逻辑推理)
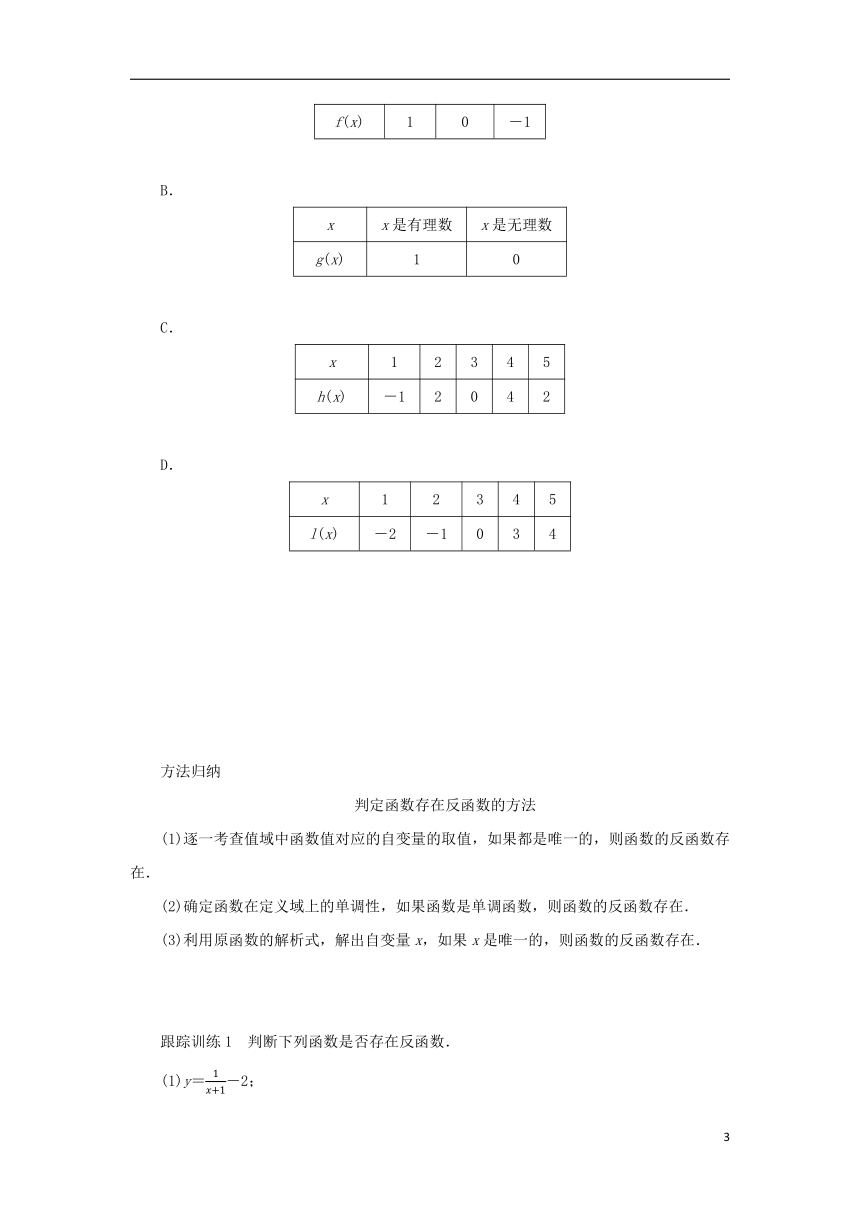
例1 下列函数中,存在反函数的是( )
A.
x x>0 x=0 x<0
f(x) 1 0 -1
B.
x x是有理数 x是无理数
g(x) 1 0
C.
x 1 2 3 4 5
h(x) -1 2 0 4 2
D.
x 1 2 3 4 5
l(x) -2 -1 0 3 4
方法归纳
判定函数存在反函数的方法
(1)逐一考查值域中函数值对应的自变量的取值,如果都是唯一的,则函数的反函数存在.
(2)确定函数在定义域上的单调性,如果函数是单调函数,则函数的反函数存在.
(3)利用原函数的解析式,解出自变量x,如果x是唯一的,则函数的反函数存在.
跟踪训练1 判断下列函数是否存在反函数.
(1)y=-2;
(2)y=-2x2+4x,x∈(1,+∞).
题型2 求函数的反函数
例2 求下列函数的反函数.
1.判断函数是否单调.
2.求出x.
3.推导出f-1(x)的解析式.
(1)y=()x
(2)y=5x+1.
方法归纳
求给定解析式的函数的反函数的步骤
(1)求出原函数的值域,这就是反函数的定义域;
(2)从y=f(x)中解出x;
(3)x,y互换并注明反函数的定义域.
跟踪训练2 求下列函数的反函数.
1.函数在定义域内的值域.
2.求x.
3.解出f -1(x).
(1)y=2x+3;
(2)y=x;
(3)y=-1;
(4)y=0.2x+1(x≤1).
题型3 反函数性质的应用
例3 (1)已知函数y=ax+b的图象过点(1,4),其反函数的图象过点(2,0),求a,b的值.
函数与反函数图象上相应点关于y=x对称.
(2)若函数f(x)=,则f-1(2)的值为( )
反函数的自变量值即原函数的函数值.
A.5 B.-5
C. D.4
方法归纳
利用反函数的性质解题
互为反函数的图象关于直线y=x对称是反函数的重要性质,由此可得互为反函数图象上任一成对的相应点也关于y=x对称,所以若点 (a,b)在函数y=f(x)的图象上,则点(b,a)必在其反函数y=f-1(x)的图象上.
跟踪训练3 (1)已知函数f(x)=ax+b(a>0且a≠1)的图象过点(1,7),其反函数f-1(x)的图象过点(4,0),求f(x)的表达式.
两点关于y=x对称.
(2)已知函数f(x)=1+2lgx,则f(1)+f-1(1)=( )
A.0 B.1
C.2 D.3
题型4 指数函数与对数函数图象间的关系
(1)由lg a+lg b=0得ab=1.
(2)f(x)与y(x)互为反函数.
例4 已知lga+lgb=0,函数f(x)=ax与函数g(x)=-logbx的图象可能是( )
方法归纳
利用反函数的性质识图
指数函数与对数函数互为反函数,二者的图象关于直线y=x对称,在有关指数函数与对数函数的图象知识问题中利用这一性质,结合平移翻转等可以很方便地解决问题.
跟踪训练4 y=log2x的反函数是y=f-1(x),则函数y=f-1(1-x)的图象是下图中的( )
状元随笔 1.先求出f -1(x).
2.再求f -1(-x).
3.最后求出f -1(1-x).
4.3 指数函数与对数函数的关系
新知初探·自主学习
知识点一
1.(1)任意一个y的值 唯一的x
知识点三
(2)定义域 值域 值域 定义域 (3)相同
知识点四
R (0,+∞) (0,+∞) R 减函数 增函数
[基础自测]
1.解析:∵g(x)=22x=4x,∴函数f(x)=log4x与g(x)=22x互为反函数,它们的图象关于直线y=x对称.
答案:D
2.解析:由于函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,则f(x)=logax,
则f(2)=loga2=1,解得a=2,因此,f(x)=log2x.
答案:B
3.解析:令2x=1,则x=0,所以f-1(1)=0.
答案:0
4.解析:结合函数与反函数关于y=x对称得出,即可得出反函数位于第一、四象限.
答案:D
课堂探究·素养提升
例1 【解析】 对A,因为f(x)=1时,x为任意的正实数,即对应的x不唯一,因此f(x)的反函数不存在;
对B,因为g(x)=1时,x为任意的有理数,即对应的x不唯一,因此g(x)的反函数不存在;
对C,因为h(x)=2时,x=2或x=5,即对应的x不唯一,因此h(x)的反函数不存在;
对D,因为l(x)的值域为{-2,-1,0,3,4}中任意一个值,都只有唯一的x与之对应,因此l(x)的反函数存在.
【答案】 D
跟踪训练1 解析:(1)y=-2是由函数y=向左平移1个单位,向下平移2个单位得到,在(-∞,-1),(-1,+∞)上是减函数,因此任意给定值域中的一个值,只有唯一的x值与之对应,所以函数存在反函数.
(2)y=-2x2+4x=-2(x-1)2+2,对称轴为x=1,在(1,+∞)上是减函数,因此任意给定值域中的一个值,只有唯一的x值与之对应,所以函数存在反函数.
例2 【解析】 (1)由y=()x得y>0,对调其中的x和y,得x=()y,解得y=x,所以f-1(x)=x(x>0).
(2)对调x与y得x=5y+1(x∈R),化简得y=,
所以f-1(x)=(x∈R).
跟踪训练2 解析:(1)由y=2x+3得x=y-,
所以函数y=2x+3的反函数是y=x-.
(2)y=x的底数是,它的反函数是指数函数y=.
(3)y=-1的值域是(-1,+∞),所以它的反函数为函数y= (x+1)(x>-1).
(4)因为y=0.2x+1,所以y-1=0.2x,x=log0.2(y-1),即y=log0.2(x-1),
因为函数y=0.2x+1(x≤1)的值域是{y|y≥1.2},所以y=log0.2(x-1)的定义域为{x|x≥1.2},即函数y=0.2x+1(x≤1)的反函数是y=log0.2(x-1)(x≥1.2).
例3 【解析】 (1)方法一 ∵y=ax+b的图象过点(1,4),
∴a+b=4,①
由y=ax+b得ax=y-b,
∴x=loga(y-b),交换x,y得y=loga(x-b),
将点(2,0)代入y=loga(x-b)得loga(2-b)=0,
∴2-b=1.②
由①②解得
方法二 ∵y=ax+b的图象过点(1,4),∴a+b=4.①
又∵y=ax+b的反函数图象过点(2,0),
∴点(0,2)在原函数y=ax+b的图象上,
∴a0+b=2.②
联立①②得
(2)令=2,所以x=-5,
所以f-1(2)=-5.
【答案】 (1)见解析 (2)B
跟踪训练3 解析:(1)∵y=f-1(x)的图象过点(4,0),∴y=f(x)的图象过点(0,4),
∴1+b=4,∴b=3,又∵f(x)=ax+b的图象过点(1,7),
∴a+b=7,∴a=4.∴f(x)=4x+3.
(2)根据题意:f(1)=1+2lg1=1,
若f(x)=1+2lgx=1,解得x=1,
则f-1(1)=1,故f(1)+f-1(1)=1+1=2.
答案:(1)见解析 (2)C
例4 【解析】 ∵lga+lgb=0,∴ab=1,则b=,从而g(x)=-logbx=logax,故g(x)与f(x)=ax互为反函数,图象关于直线y=x对称.结合选项可知选B.
【答案】 B
跟踪训练4 解析:∵y=log2x的反函数为y=f-1(x)=2x,则y=f-1(1-x)=21-x=2·2-x=2·,故排除A,B.又此函数图象过(0,2),故正确答案为C.
答案:C
5
【课程标准】
(1)了解反函数的定义.
(2)了解指数函数与对数函数互为反函数.
新知初探·自主学习——突出基础性
教材要点
知识点一 反函数的定义
(1)定义:如果在函数y=f(x)中,给定值域中________________,只有________与之对应,那么x是y的函数,这个函数称为y=f(x)的反函数.
(2)记法:y=f-1(x).
状元随笔 1.函数f(x)=x2有反函数吗?为什么?
提示:没有.若令y=f(x)=1,则x=±1,即x值不唯一,不符合反函数的定义.
2.什么样的函数一定有反函数?
提示:单调函数.
知识点二 反函数的求法
对调y=f(x)中的x与y,然后从x=f(y)中求出y得到.
知识点三 函数与其反函数的性质的关系
(1)图象:关于直线y=x对称;
(2)定义域、值域:原函数的________与其反函数的________相同;原函数的________与其反函数的________相同.
(3)单调性:原函数与其反函数的单调性________.
知识点四 指数函数与对数函数的性质
函数 指数函数y=ax 对数函数y=logax
定义域 ________ ________
值域 ________ ________
单调性 0
状元随笔 指数函数y=ax与对数函数y=logax,一个函数的定义域是另一个函数的值域,而且它们的单调性相同.
基础自测
1.函数f(x)=log4x与g(x)=4x的图象( )
A.关于x轴对称 B.关于y轴对称
C.关于原点对称 D.关于直线y=x对称
2.若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=( )
A. B.log2x
C.x D.2x-2
3.若函数f(x)=2x的反函数为f-1(x),则f-1(1)=________.
4.若函数y=f(x)的图象位于第一、二象限,则它的反函数y=f-1(x)的图象位于( )
A.第一、二象限 B.第三、四象限
C.第二、三象限 D.第一、四象限
课堂探究·素养提升——强化创新性
题型1 判断函数是否有反函数(逻辑推理)
例1 下列函数中,存在反函数的是( )
A.
x x>0 x=0 x<0
f(x) 1 0 -1
B.
x x是有理数 x是无理数
g(x) 1 0
C.
x 1 2 3 4 5
h(x) -1 2 0 4 2
D.
x 1 2 3 4 5
l(x) -2 -1 0 3 4
方法归纳
判定函数存在反函数的方法
(1)逐一考查值域中函数值对应的自变量的取值,如果都是唯一的,则函数的反函数存在.
(2)确定函数在定义域上的单调性,如果函数是单调函数,则函数的反函数存在.
(3)利用原函数的解析式,解出自变量x,如果x是唯一的,则函数的反函数存在.
跟踪训练1 判断下列函数是否存在反函数.
(1)y=-2;
(2)y=-2x2+4x,x∈(1,+∞).
题型2 求函数的反函数
例2 求下列函数的反函数.
1.判断函数是否单调.
2.求出x.
3.推导出f-1(x)的解析式.
(1)y=()x
(2)y=5x+1.
方法归纳
求给定解析式的函数的反函数的步骤
(1)求出原函数的值域,这就是反函数的定义域;
(2)从y=f(x)中解出x;
(3)x,y互换并注明反函数的定义域.
跟踪训练2 求下列函数的反函数.
1.函数在定义域内的值域.
2.求x.
3.解出f -1(x).
(1)y=2x+3;
(2)y=x;
(3)y=-1;
(4)y=0.2x+1(x≤1).
题型3 反函数性质的应用
例3 (1)已知函数y=ax+b的图象过点(1,4),其反函数的图象过点(2,0),求a,b的值.
函数与反函数图象上相应点关于y=x对称.
(2)若函数f(x)=,则f-1(2)的值为( )
反函数的自变量值即原函数的函数值.
A.5 B.-5
C. D.4
方法归纳
利用反函数的性质解题
互为反函数的图象关于直线y=x对称是反函数的重要性质,由此可得互为反函数图象上任一成对的相应点也关于y=x对称,所以若点 (a,b)在函数y=f(x)的图象上,则点(b,a)必在其反函数y=f-1(x)的图象上.
跟踪训练3 (1)已知函数f(x)=ax+b(a>0且a≠1)的图象过点(1,7),其反函数f-1(x)的图象过点(4,0),求f(x)的表达式.
两点关于y=x对称.
(2)已知函数f(x)=1+2lgx,则f(1)+f-1(1)=( )
A.0 B.1
C.2 D.3
题型4 指数函数与对数函数图象间的关系
(1)由lg a+lg b=0得ab=1.
(2)f(x)与y(x)互为反函数.
例4 已知lga+lgb=0,函数f(x)=ax与函数g(x)=-logbx的图象可能是( )
方法归纳
利用反函数的性质识图
指数函数与对数函数互为反函数,二者的图象关于直线y=x对称,在有关指数函数与对数函数的图象知识问题中利用这一性质,结合平移翻转等可以很方便地解决问题.
跟踪训练4 y=log2x的反函数是y=f-1(x),则函数y=f-1(1-x)的图象是下图中的( )
状元随笔 1.先求出f -1(x).
2.再求f -1(-x).
3.最后求出f -1(1-x).
4.3 指数函数与对数函数的关系
新知初探·自主学习
知识点一
1.(1)任意一个y的值 唯一的x
知识点三
(2)定义域 值域 值域 定义域 (3)相同
知识点四
R (0,+∞) (0,+∞) R 减函数 增函数
[基础自测]
1.解析:∵g(x)=22x=4x,∴函数f(x)=log4x与g(x)=22x互为反函数,它们的图象关于直线y=x对称.
答案:D
2.解析:由于函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,则f(x)=logax,
则f(2)=loga2=1,解得a=2,因此,f(x)=log2x.
答案:B
3.解析:令2x=1,则x=0,所以f-1(1)=0.
答案:0
4.解析:结合函数与反函数关于y=x对称得出,即可得出反函数位于第一、四象限.
答案:D
课堂探究·素养提升
例1 【解析】 对A,因为f(x)=1时,x为任意的正实数,即对应的x不唯一,因此f(x)的反函数不存在;
对B,因为g(x)=1时,x为任意的有理数,即对应的x不唯一,因此g(x)的反函数不存在;
对C,因为h(x)=2时,x=2或x=5,即对应的x不唯一,因此h(x)的反函数不存在;
对D,因为l(x)的值域为{-2,-1,0,3,4}中任意一个值,都只有唯一的x与之对应,因此l(x)的反函数存在.
【答案】 D
跟踪训练1 解析:(1)y=-2是由函数y=向左平移1个单位,向下平移2个单位得到,在(-∞,-1),(-1,+∞)上是减函数,因此任意给定值域中的一个值,只有唯一的x值与之对应,所以函数存在反函数.
(2)y=-2x2+4x=-2(x-1)2+2,对称轴为x=1,在(1,+∞)上是减函数,因此任意给定值域中的一个值,只有唯一的x值与之对应,所以函数存在反函数.
例2 【解析】 (1)由y=()x得y>0,对调其中的x和y,得x=()y,解得y=x,所以f-1(x)=x(x>0).
(2)对调x与y得x=5y+1(x∈R),化简得y=,
所以f-1(x)=(x∈R).
跟踪训练2 解析:(1)由y=2x+3得x=y-,
所以函数y=2x+3的反函数是y=x-.
(2)y=x的底数是,它的反函数是指数函数y=.
(3)y=-1的值域是(-1,+∞),所以它的反函数为函数y= (x+1)(x>-1).
(4)因为y=0.2x+1,所以y-1=0.2x,x=log0.2(y-1),即y=log0.2(x-1),
因为函数y=0.2x+1(x≤1)的值域是{y|y≥1.2},所以y=log0.2(x-1)的定义域为{x|x≥1.2},即函数y=0.2x+1(x≤1)的反函数是y=log0.2(x-1)(x≥1.2).
例3 【解析】 (1)方法一 ∵y=ax+b的图象过点(1,4),
∴a+b=4,①
由y=ax+b得ax=y-b,
∴x=loga(y-b),交换x,y得y=loga(x-b),
将点(2,0)代入y=loga(x-b)得loga(2-b)=0,
∴2-b=1.②
由①②解得
方法二 ∵y=ax+b的图象过点(1,4),∴a+b=4.①
又∵y=ax+b的反函数图象过点(2,0),
∴点(0,2)在原函数y=ax+b的图象上,
∴a0+b=2.②
联立①②得
(2)令=2,所以x=-5,
所以f-1(2)=-5.
【答案】 (1)见解析 (2)B
跟踪训练3 解析:(1)∵y=f-1(x)的图象过点(4,0),∴y=f(x)的图象过点(0,4),
∴1+b=4,∴b=3,又∵f(x)=ax+b的图象过点(1,7),
∴a+b=7,∴a=4.∴f(x)=4x+3.
(2)根据题意:f(1)=1+2lg1=1,
若f(x)=1+2lgx=1,解得x=1,
则f-1(1)=1,故f(1)+f-1(1)=1+1=2.
答案:(1)见解析 (2)C
例4 【解析】 ∵lga+lgb=0,∴ab=1,则b=,从而g(x)=-logbx=logax,故g(x)与f(x)=ax互为反函数,图象关于直线y=x对称.结合选项可知选B.
【答案】 B
跟踪训练4 解析:∵y=log2x的反函数为y=f-1(x)=2x,则y=f-1(1-x)=21-x=2·2-x=2·,故排除A,B.又此函数图象过(0,2),故正确答案为C.
答案:C
5
