人教版八年级上册11.2.2三角形的外角课时练习 (含解析)
文档属性
| 名称 | 人教版八年级上册11.2.2三角形的外角课时练习 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 368.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览

文档简介
三角形的外角
一、单选题
1.三角形的一个外角为36°,则这个三角形一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
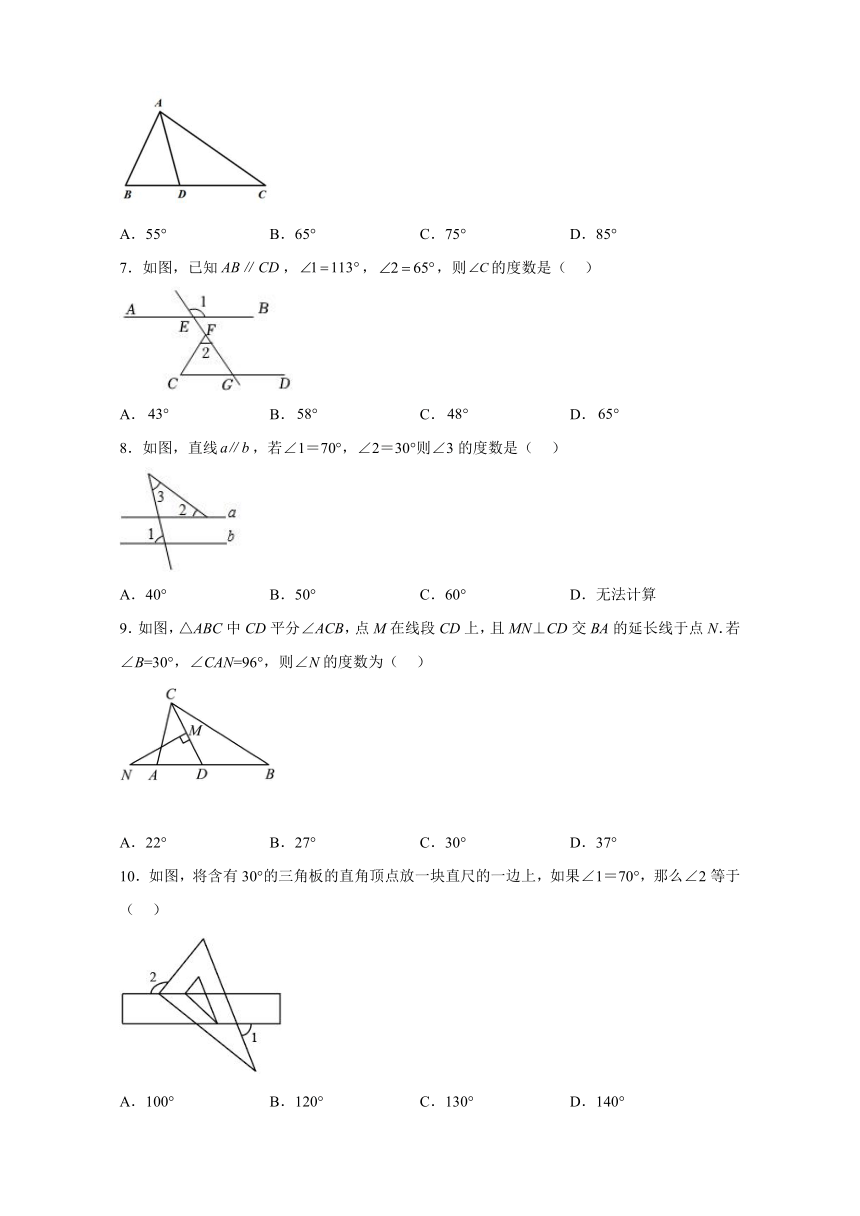
2.已知,如图,∠A=70°,∠B=40°,CD平分∠ACE,则∠ACD=( )
A.55° B.70° C.40° D.110°
3.如图,将一副直角三角板按如图所示的位置放置,则∠AOD的度数是( )
A.85° B.90° C.75° D.105°
4.如图,将直尺与含30°角的三角尺摆放在一起,若,则的度数是( )
A.45° B.50° C.55° D.65°
5.如图,将一副三角板如图所示摆放,其中点在上,,,,则等于( )
A.15° B.30° C.12° D.35°
6.如图,在△ABC中,AD平分∠BAC,∠B=65°,∠C=35°,则∠ADB的度数为( )
A.55° B.65° C.75° D.85°
7.如图,已知,,,则的度数是( )
A. B. C. D.
8.如图,直线,若∠1=70°,∠2=30°则∠3的度数是( )
A.40° B.50° C.60° D.无法计算
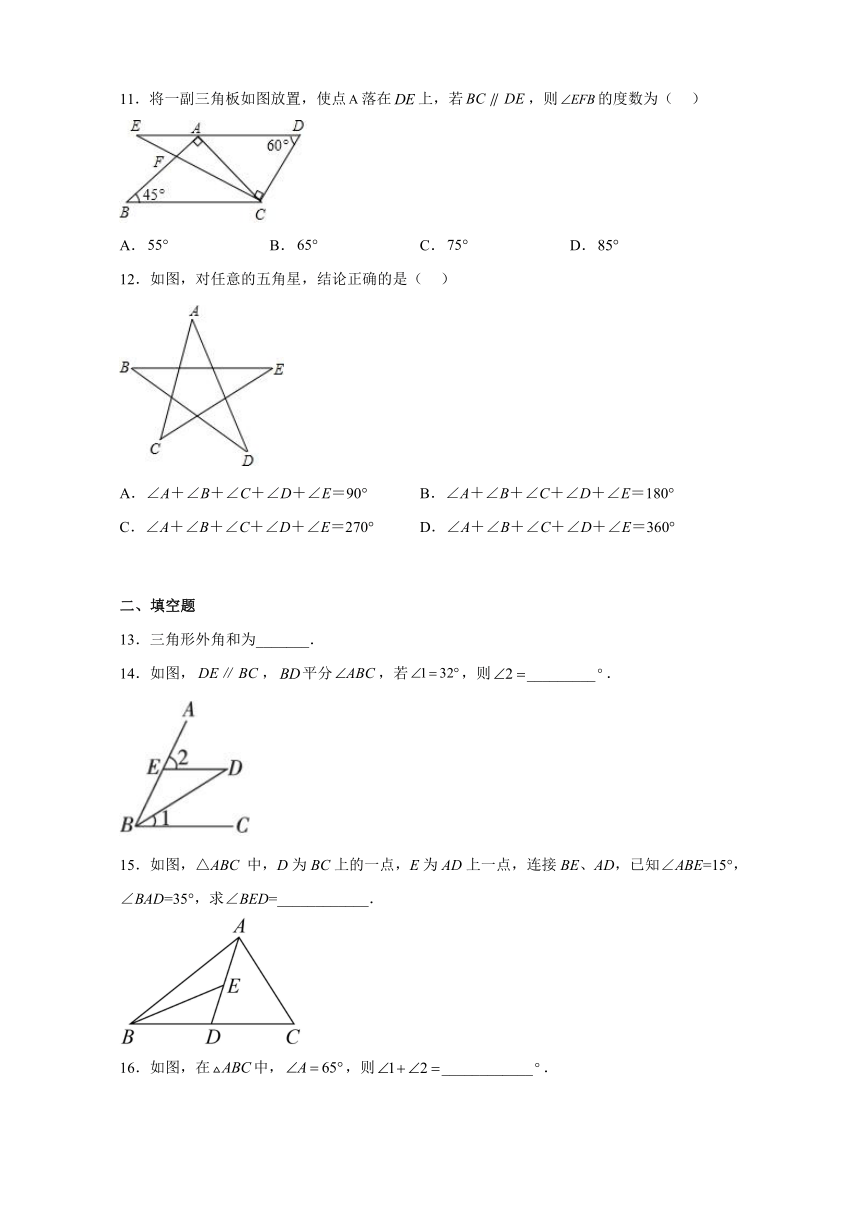
9.如图,△ABC中CD平分∠ACB,点M在线段CD上,且MN⊥CD交BA的延长线于点N.若∠B=30°,∠CAN=96°,则∠N的度数为( )
A.22° B.27° C.30° D.37°
10.如图,将含有30°的三角板的直角顶点放一块直尺的一边上,如果∠1=70°,那么∠2等于( )
A.100° B.120° C.130° D.140°
11.将一副三角板如图放置,使点落在上,若,则的度数为( )
A. B. C. D.
12.如图,对任意的五角星,结论正确的是( )
A.∠A+∠B+∠C+∠D+∠E=90° B.∠A+∠B+∠C+∠D+∠E=180°
C.∠A+∠B+∠C+∠D+∠E=270° D.∠A+∠B+∠C+∠D+∠E=360°
二、填空题
13.三角形外角和为_______.
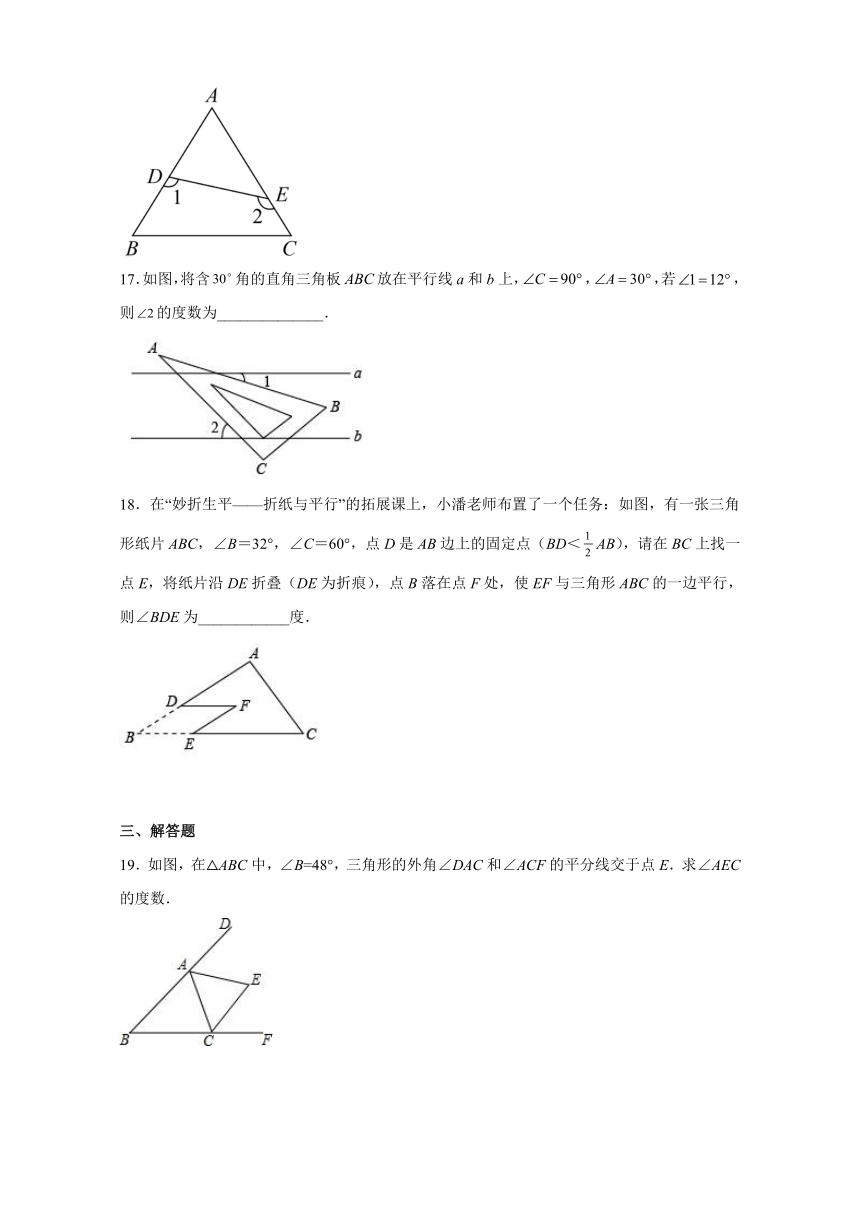
14.如图,,平分,若,则_________.
15.如图,△ABC 中,D为BC上的一点,E为AD上一点,连接BE、AD,已知∠ABE=15°,∠BAD=35°,求∠BED=____________.
16.如图,在中,,则____________.
17.如图,将含角的直角三角板放在平行线a和b上,,,若,则的度数为______________.
18.在“妙折生平——折纸与平行”的拓展课上,小潘老师布置了一个任务:如图,有一张三角形纸片ABC,∠B=32°,∠C=60°,点D是AB边上的固定点(BD<AB),请在BC上找一点E,将纸片沿DE折叠(DE为折痕),点B落在点F处,使EF与三角形ABC的一边平行,则∠BDE为____________度.
三、解答题
19.如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E.求∠AEC的度数.
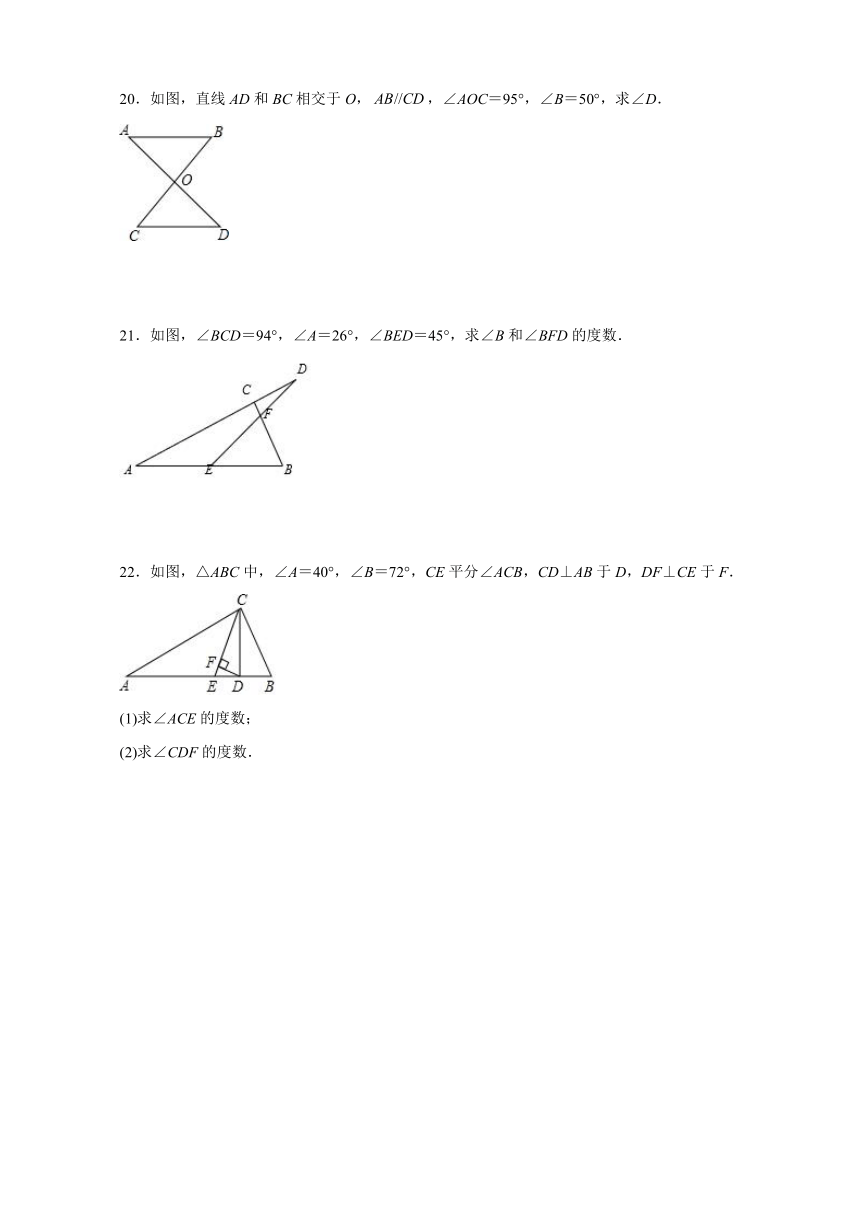
20.如图,直线AD和BC相交于O,,∠AOC=95°,∠B=50°,求∠D.
21.如图,∠BCD=94°,∠A=26°,∠BED=45°,求∠B和∠BFD的度数.
22.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F.
(1)求∠ACE的度数;
(2)求∠CDF的度数.
参考答案:
1.B
解:∵ 三角形的一个外角是36°
∴ 对应的内角为
∴ 这个三角形是钝角三角形
故选:B
2.A
解:∵∠ACE是△ABC的外角,∠A=70°,∠B=40°,
∴∠ACE=∠A+∠B=110°,
∵CD平分∠ACE,
∴∠ACD=∠ACE=55°.
故选:A.
3.D
解:由题意得:∠BCD=60°,∠ACB=45°,∠D=90°,
∴∠DCO=∠BCD-∠ACB=15°,
∵∠AOD是△DCO的外角,
∴∠AOD=∠D+∠DCO=105°.
故选:D.
4.C
解:如图:
∵∠3是△EFH的一个外角,
∴∠3=∠1+∠F=25°+30°=55°,
∵ABCD,
∴∠2=∠3=55°,
故选:C.
5.A
解:如图:∵AB//DE
∴∠FGB=∠D=45°
∵∠FGB=∠A+∠GFA,∠A=30°
∴∠AFD=15°
故选:A.
6.C
解:∵在△ABC中,∠B=65°,∠C=35°,
∴∠BAC=180° ∠B ∠C=180° 65° 35°=80°,
∵AD平分∠BAC,
∴∠DAC=∠BAC=40°,
∴∠ADB=∠DAC+∠C=40°+35°=75°,
故选:C.
7.C
解:,,
.
,,
.
故选:.
8.A
解:如图.
∵ab,∠1=70°,
∴∠4=∠1=70°,
∵∠4=∠3+∠2,∠2=30°,
∴∠3=∠4 ∠2=70° 30°=40°,
故选:A.
9.B
解:∵∠CAN是△ABC的外角,
∴∠CAN=∠B+∠ACB,
∵∠B=30°,∠CAN=96°,
∴∠ACB=96°-30°=66°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=33°,
∵∠CDN是△BCD的外角,
∴∠CDN=∠B+∠BCD=63°,
∵△DMN中,∠DMN=90°,∠MDN=63°,
∴∠N=180°-∠DMN-∠MDN=27°,
故选: B.
10.C
解:如图:
,,
,
,
,,
.
故选:C.
11.C
解:由题意得:,
,
,
,
故选:C.
12.B
解:∵∠1=∠2+∠D,
∠2=∠A+∠C,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
故选:B.
13.360°
解:三角形的外角和为360°,
故答案为:360°.
14.64
解:∵,
∴∠D=∠ABD,
∵平分,,
∴∠ABD=∠1=32°,
∴∠D=32°,
∴∠2=∠D+∠ABD=64°.
故答案为:64
15.50°
解:∵∠ABE=15°,∠BAD=35°,
∴∠BED=∠ABE+∠BAD=15°+35°=50°,
故答案为:50°.
16.
解:∵,
∴.
∵,,
∴.
故答案为:.
17.
解:如图,AB与直线a相交于点M,
∵∠1=∠AMN,∠1=12°,
∴∠AMN=12°,
∵∠A=30°,
∴∠3=∠A+∠AMN=42°,
∵,
∴∠2=∠3=42°;
故答案为:42°
18.28°或74°或118°
解:当时,
由折叠得,∠B=∠F=32°,∠BED=∠DEF,
∵,
∴∠B=∠CEF=32°,
∴∠BEF=180°-32°=148°,
∴;
当时,
∵,
∴∠BEF=∠C=60°,
∴,
∴;
当时,
∴∠CEF=∠C=60°,
∴∠BGD=∠CEF+∠F=92°,
∴∠BDG=180°-∠B-∠BGD=56°,
∴;
综上所述,∠BDE为28°或74°或118°.
故答案为:28°或74°或118°
19.66°
解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠CAE+∠ACE=(∠B+∠ACB)+(∠B+∠BAC)
=(∠BAC+∠B+∠ACB+∠B)
=(180°+48°)
=114 °
在△ACE中,∠AEC=180°-(∠CAE+∠ACE)
=180°-114°
=66°
20.45°
解:∵,
∴∠A=∠D,∠B=∠C,
∵∠AOC=95°,∠B=50°,
∴∠C+∠D=95°,
即50°+∠D=95°,
∴∠D=45°.
21.
解:∵∠BCD=94°,∠A=26°,∠BED=45°,
,
,
,
.
22.(1)34° (2)74°
(1)
解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=34°;
(2)
解:∵∠CED=∠A+∠ACE=74°,
∴∠CDE=90°,DF⊥CE,
∴∠CDF+∠ECD=∠ECD+∠CED=90°,
∴∠CDF=∠CED=74°.
一、单选题
1.三角形的一个外角为36°,则这个三角形一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
2.已知,如图,∠A=70°,∠B=40°,CD平分∠ACE,则∠ACD=( )
A.55° B.70° C.40° D.110°
3.如图,将一副直角三角板按如图所示的位置放置,则∠AOD的度数是( )
A.85° B.90° C.75° D.105°
4.如图,将直尺与含30°角的三角尺摆放在一起,若,则的度数是( )
A.45° B.50° C.55° D.65°
5.如图,将一副三角板如图所示摆放,其中点在上,,,,则等于( )
A.15° B.30° C.12° D.35°
6.如图,在△ABC中,AD平分∠BAC,∠B=65°,∠C=35°,则∠ADB的度数为( )
A.55° B.65° C.75° D.85°
7.如图,已知,,,则的度数是( )
A. B. C. D.
8.如图,直线,若∠1=70°,∠2=30°则∠3的度数是( )
A.40° B.50° C.60° D.无法计算
9.如图,△ABC中CD平分∠ACB,点M在线段CD上,且MN⊥CD交BA的延长线于点N.若∠B=30°,∠CAN=96°,则∠N的度数为( )
A.22° B.27° C.30° D.37°
10.如图,将含有30°的三角板的直角顶点放一块直尺的一边上,如果∠1=70°,那么∠2等于( )
A.100° B.120° C.130° D.140°
11.将一副三角板如图放置,使点落在上,若,则的度数为( )
A. B. C. D.
12.如图,对任意的五角星,结论正确的是( )
A.∠A+∠B+∠C+∠D+∠E=90° B.∠A+∠B+∠C+∠D+∠E=180°
C.∠A+∠B+∠C+∠D+∠E=270° D.∠A+∠B+∠C+∠D+∠E=360°
二、填空题
13.三角形外角和为_______.
14.如图,,平分,若,则_________.
15.如图,△ABC 中,D为BC上的一点,E为AD上一点,连接BE、AD,已知∠ABE=15°,∠BAD=35°,求∠BED=____________.
16.如图,在中,,则____________.
17.如图,将含角的直角三角板放在平行线a和b上,,,若,则的度数为______________.
18.在“妙折生平——折纸与平行”的拓展课上,小潘老师布置了一个任务:如图,有一张三角形纸片ABC,∠B=32°,∠C=60°,点D是AB边上的固定点(BD<AB),请在BC上找一点E,将纸片沿DE折叠(DE为折痕),点B落在点F处,使EF与三角形ABC的一边平行,则∠BDE为____________度.
三、解答题
19.如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E.求∠AEC的度数.
20.如图,直线AD和BC相交于O,,∠AOC=95°,∠B=50°,求∠D.
21.如图,∠BCD=94°,∠A=26°,∠BED=45°,求∠B和∠BFD的度数.
22.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F.
(1)求∠ACE的度数;
(2)求∠CDF的度数.
参考答案:
1.B
解:∵ 三角形的一个外角是36°
∴ 对应的内角为
∴ 这个三角形是钝角三角形
故选:B
2.A
解:∵∠ACE是△ABC的外角,∠A=70°,∠B=40°,
∴∠ACE=∠A+∠B=110°,
∵CD平分∠ACE,
∴∠ACD=∠ACE=55°.
故选:A.
3.D
解:由题意得:∠BCD=60°,∠ACB=45°,∠D=90°,
∴∠DCO=∠BCD-∠ACB=15°,
∵∠AOD是△DCO的外角,
∴∠AOD=∠D+∠DCO=105°.
故选:D.
4.C
解:如图:
∵∠3是△EFH的一个外角,
∴∠3=∠1+∠F=25°+30°=55°,
∵ABCD,
∴∠2=∠3=55°,
故选:C.
5.A
解:如图:∵AB//DE
∴∠FGB=∠D=45°
∵∠FGB=∠A+∠GFA,∠A=30°
∴∠AFD=15°
故选:A.
6.C
解:∵在△ABC中,∠B=65°,∠C=35°,
∴∠BAC=180° ∠B ∠C=180° 65° 35°=80°,
∵AD平分∠BAC,
∴∠DAC=∠BAC=40°,
∴∠ADB=∠DAC+∠C=40°+35°=75°,
故选:C.
7.C
解:,,
.
,,
.
故选:.
8.A
解:如图.
∵ab,∠1=70°,
∴∠4=∠1=70°,
∵∠4=∠3+∠2,∠2=30°,
∴∠3=∠4 ∠2=70° 30°=40°,
故选:A.
9.B
解:∵∠CAN是△ABC的外角,
∴∠CAN=∠B+∠ACB,
∵∠B=30°,∠CAN=96°,
∴∠ACB=96°-30°=66°,
∵CD平分∠ACB,
∴∠BCD=∠ACB=33°,
∵∠CDN是△BCD的外角,
∴∠CDN=∠B+∠BCD=63°,
∵△DMN中,∠DMN=90°,∠MDN=63°,
∴∠N=180°-∠DMN-∠MDN=27°,
故选: B.
10.C
解:如图:
,,
,
,
,,
.
故选:C.
11.C
解:由题意得:,
,
,
,
故选:C.
12.B
解:∵∠1=∠2+∠D,
∠2=∠A+∠C,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
故选:B.
13.360°
解:三角形的外角和为360°,
故答案为:360°.
14.64
解:∵,
∴∠D=∠ABD,
∵平分,,
∴∠ABD=∠1=32°,
∴∠D=32°,
∴∠2=∠D+∠ABD=64°.
故答案为:64
15.50°
解:∵∠ABE=15°,∠BAD=35°,
∴∠BED=∠ABE+∠BAD=15°+35°=50°,
故答案为:50°.
16.
解:∵,
∴.
∵,,
∴.
故答案为:.
17.
解:如图,AB与直线a相交于点M,
∵∠1=∠AMN,∠1=12°,
∴∠AMN=12°,
∵∠A=30°,
∴∠3=∠A+∠AMN=42°,
∵,
∴∠2=∠3=42°;
故答案为:42°
18.28°或74°或118°
解:当时,
由折叠得,∠B=∠F=32°,∠BED=∠DEF,
∵,
∴∠B=∠CEF=32°,
∴∠BEF=180°-32°=148°,
∴;
当时,
∵,
∴∠BEF=∠C=60°,
∴,
∴;
当时,
∴∠CEF=∠C=60°,
∴∠BGD=∠CEF+∠F=92°,
∴∠BDG=180°-∠B-∠BGD=56°,
∴;
综上所述,∠BDE为28°或74°或118°.
故答案为:28°或74°或118°
19.66°
解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠CAE+∠ACE=(∠B+∠ACB)+(∠B+∠BAC)
=(∠BAC+∠B+∠ACB+∠B)
=(180°+48°)
=114 °
在△ACE中,∠AEC=180°-(∠CAE+∠ACE)
=180°-114°
=66°
20.45°
解:∵,
∴∠A=∠D,∠B=∠C,
∵∠AOC=95°,∠B=50°,
∴∠C+∠D=95°,
即50°+∠D=95°,
∴∠D=45°.
21.
解:∵∠BCD=94°,∠A=26°,∠BED=45°,
,
,
,
.
22.(1)34° (2)74°
(1)
解:∵∠A=40°,∠B=72°,
∴∠ACB=180°﹣40°﹣72°=68°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=34°;
(2)
解:∵∠CED=∠A+∠ACE=74°,
∴∠CDE=90°,DF⊥CE,
∴∠CDF+∠ECD=∠ECD+∠CED=90°,
∴∠CDF=∠CED=74°.
