黑龙江省大庆双语中学2013-2014学年八年级上学期第一次月考数学试卷(附答案)
文档属性
| 名称 | 黑龙江省大庆双语中学2013-2014学年八年级上学期第一次月考数学试卷(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-21 00:00:00 | ||
图片预览


文档简介
大庆双语中学2013-2014学年第一学期月考八年级数学试题
(试题共6页28题 考试时间:90分钟 总分:100分 )
题号 一 二 三 总 分
得分
一、填空题:(每题3分,共30分)
1、如图,一面小红旗其中∠A=60°, ∠B=30°,则∠BCD= 。
2、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是___________________.
3、把一副常用的三角板如图所示拼在一起,那么图中∠ADE是 度。
4、如4题图,△ABC≌△EDF,DF=BC,AB=ED,AF=20,EC=10,则AE的长是 。
5、在△ABC中,∠A=100°,∠B=3∠C,则∠B=________.
6、如图,⊿ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF = 度。
7、若一个等腰三角形的两边长分别是4cm和9cm,则其周长是________.
8、如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为________.
9、 一个多边形的每个内角都等于150°,则这个多边形是_____边形.
10、如图ABC中,AD是BC上的中线,BE是ABD中AD边上的中线,若ABC的面积是24cm2,则ABE的面积是________。
二、选择题:(每题2分,共20分)
11、要组成一个三角形,三条线段长度可取( )
A.3,5,9 B.2,3,5 C.18,9,8 D.9,6,13
12、如图,∠A+∠B+∠C+∠D+∠E+∠F的和为( )
A.180° B.360° C.540° D.720°
13、直角三角形的两个锐角平分线所夹的锐角是( )
A.30° B.60° C.45° D.15°和75°
14、锐角三角形中,任意两个锐角的和必大于( )
A.90° B.110° C.100° D.120°
15、以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )(A)1个 (B)2个 (C)3个 (D)4个
16、若一个n边形n个内角与某一个外角的总和为1350°,则n等于( )
A.6 B.7 C.8 D.9
17、如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,
∠AFD=158°, 则∠EDF=________度.
A.58° B.68° C.78° D.32°
18、已知有两边相等的三角形两边长分别为6cm、4cm,则该三角形的周长是( )
A.16cm B.14cm C.16cm或14cm D.10cm
19、七边形有( )条对角线.
A.11 B.12 C.13 D.14
20、四边形的内角和与外角和的和是( )
A. 720° B.180° C.540° D.360°
三、解答题:(50分)
21、(6分)如图,已知: AD∥BC,AD=CB,AE=CF. 求证:∠D=∠B.
证明:∵AD∥BC,
∴∠A=∠ ( ).
∵AE=CF,
∴AE+ =CF+ ( )
∴AF= .
在△AFD和△CEB中,
( )
∴△AFD≌△CEB( ).
∴∠D=∠B( ).
22、(5分)如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,
∠BDC=95°,求△BDE各内角的度数.
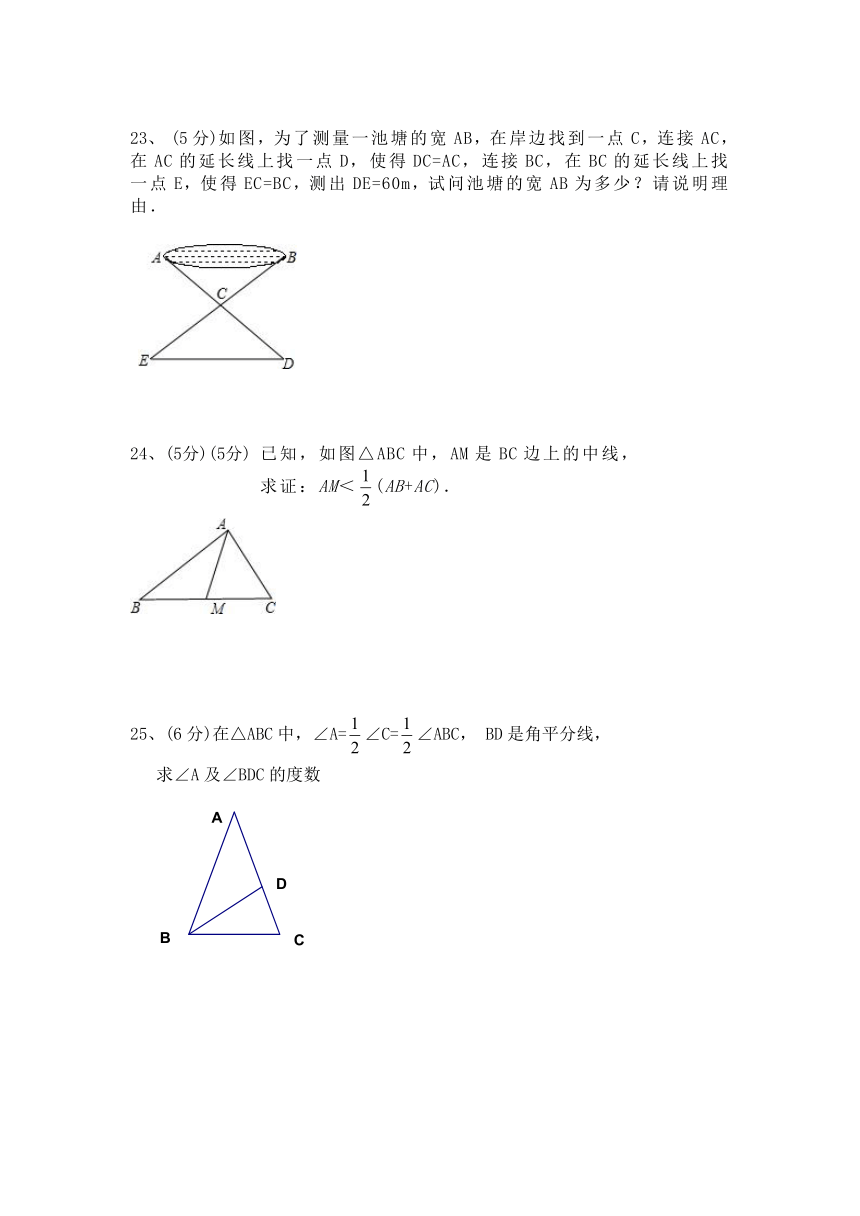
23、 (5分)如图,为了测量一池塘的宽AB,在岸边找到一点C,连接AC,在AC的延长线上找一点D,使得DC=AC,连接BC,在BC的延长线上找一点E,使得EC=BC,测出DE=60m,试问池塘的宽AB为多少?请说明理由.
24、(5分)(5分) 已知,如图△ABC中,AM是BC边上的中线,
求证:AM<(AB+AC).
25、(6分)在△ABC中,∠A=∠C=∠ABC, BD是角平分线,
求∠A及∠BDC的度数
26、(5分)已知:如图,AB=AC,∠BAC=∠DAE,AD=AE.
求证:BD=CE.
27、(8分)如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB,②AE=CF,③∠B=∠D,④AD∥BC.请用其中三个作为已知条件,余下一个作为求证结论,编一道数学问题,并写出解答过程:
已知条件: , , ;
求证结论: .
证明:
28、(10分)探究:
(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,
填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),
当∠A=40°时,∠B+∠C+∠1+∠2=______
(3)如图③,是由图①的△ABC沿DE折叠得到的,
如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,
猜想∠BDA+∠CEA与∠A的关系为
图① 图② 图③
2013-2014学年第一学期月考八年级数学试题
参考答案:
1.900; 2.三角形的稳定性; 3.135; 4.5; 5.∠B=60°;
6.74; 7. 22; 8.800; 9.十二边形; 10.6cm2;
11、选D。12、选B。13、选C;14、选A。15、选C; 16、选D。17、选B。18、选C。19、选D。20、选A。
21、
22、解:∠C=180°-∠ABC-∠A=180°-60°-70°=50°.
23、
解:AB=60米.
理由如下:∵在△ABC和△DEC中,
AC=DC
∠ACB=∠DCE
BC=EC.,
∴△ABC≌△DEC(SAS),
∴AB=DE=60(米),
则池塘的宽AB为60米
24、证明:延长AM到D,使MD=AM,连CD,
∵AM是BC边上的中线,∴BM=CM,
又AM=DM,∠AMB=∠CMD,
∴△ABM≌△DCM,∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
AM<(AB+AC).
25、因为BD是ABC的角平分线
所以∠ABD=∠DBC=ABC
因为∠A=∠C=∠ABC
所以∠A=∠ABD=∠DBC
因为∠BDC是∠A和∠ABD的外角
所以∠BDC=∠A+∠ABD=∠DBC+∠ABD=∠ABC=∠C
设∠A=x
则∠A+∠ABD+∠C=180=5x
x=36
所以∠A=36°
∠BDC=72°
26、证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠EAC,
在△BAD和△EAC中
AB=AC
∠BAD=∠EAC
AD=AE
∴BD=EC
27、证明:已知条件:AD∥BC,AE=CF,AD=BC,
求证结论:∠B=∠D.
证明:∵AE=CF,
∴AE+EF=CF+EF.
∴AF=CE.
∵AD∥BC,
∴∠A=∠C.
在△ADF和△CBE中
AD=BC,∠A=∠C,AF=CE,
∴△ADF≌△CBE.
∴∠B=∠D.
28、解:(1)根据三角形内角是180°可知:∠1+∠2=180°-∠A,∠B+∠C=180°-∠A,
∴∠1+∠2=∠B+∠C;
(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,
∴∠1+∠2=∠B+∠C;
当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°;
(3)如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°-300°=60°,
所以∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
第1题图
第4题图
第2题图
第3题图
第10题图
第8题图
第6题图
(试题共6页28题 考试时间:90分钟 总分:100分 )
题号 一 二 三 总 分
得分
一、填空题:(每题3分,共30分)
1、如图,一面小红旗其中∠A=60°, ∠B=30°,则∠BCD= 。
2、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是___________________.
3、把一副常用的三角板如图所示拼在一起,那么图中∠ADE是 度。
4、如4题图,△ABC≌△EDF,DF=BC,AB=ED,AF=20,EC=10,则AE的长是 。
5、在△ABC中,∠A=100°,∠B=3∠C,则∠B=________.
6、如图,⊿ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF = 度。
7、若一个等腰三角形的两边长分别是4cm和9cm,则其周长是________.
8、如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为________.
9、 一个多边形的每个内角都等于150°,则这个多边形是_____边形.
10、如图ABC中,AD是BC上的中线,BE是ABD中AD边上的中线,若ABC的面积是24cm2,则ABE的面积是________。
二、选择题:(每题2分,共20分)
11、要组成一个三角形,三条线段长度可取( )
A.3,5,9 B.2,3,5 C.18,9,8 D.9,6,13
12、如图,∠A+∠B+∠C+∠D+∠E+∠F的和为( )
A.180° B.360° C.540° D.720°
13、直角三角形的两个锐角平分线所夹的锐角是( )
A.30° B.60° C.45° D.15°和75°
14、锐角三角形中,任意两个锐角的和必大于( )
A.90° B.110° C.100° D.120°
15、以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )(A)1个 (B)2个 (C)3个 (D)4个
16、若一个n边形n个内角与某一个外角的总和为1350°,则n等于( )
A.6 B.7 C.8 D.9
17、如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,
∠AFD=158°, 则∠EDF=________度.
A.58° B.68° C.78° D.32°
18、已知有两边相等的三角形两边长分别为6cm、4cm,则该三角形的周长是( )
A.16cm B.14cm C.16cm或14cm D.10cm
19、七边形有( )条对角线.
A.11 B.12 C.13 D.14
20、四边形的内角和与外角和的和是( )
A. 720° B.180° C.540° D.360°
三、解答题:(50分)
21、(6分)如图,已知: AD∥BC,AD=CB,AE=CF. 求证:∠D=∠B.
证明:∵AD∥BC,
∴∠A=∠ ( ).
∵AE=CF,
∴AE+ =CF+ ( )
∴AF= .
在△AFD和△CEB中,
( )
∴△AFD≌△CEB( ).
∴∠D=∠B( ).
22、(5分)如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,
∠BDC=95°,求△BDE各内角的度数.
23、 (5分)如图,为了测量一池塘的宽AB,在岸边找到一点C,连接AC,在AC的延长线上找一点D,使得DC=AC,连接BC,在BC的延长线上找一点E,使得EC=BC,测出DE=60m,试问池塘的宽AB为多少?请说明理由.
24、(5分)(5分) 已知,如图△ABC中,AM是BC边上的中线,
求证:AM<(AB+AC).
25、(6分)在△ABC中,∠A=∠C=∠ABC, BD是角平分线,
求∠A及∠BDC的度数
26、(5分)已知:如图,AB=AC,∠BAC=∠DAE,AD=AE.
求证:BD=CE.
27、(8分)如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB,②AE=CF,③∠B=∠D,④AD∥BC.请用其中三个作为已知条件,余下一个作为求证结论,编一道数学问题,并写出解答过程:
已知条件: , , ;
求证结论: .
证明:
28、(10分)探究:
(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,
填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),
当∠A=40°时,∠B+∠C+∠1+∠2=______
(3)如图③,是由图①的△ABC沿DE折叠得到的,
如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,
猜想∠BDA+∠CEA与∠A的关系为
图① 图② 图③
2013-2014学年第一学期月考八年级数学试题
参考答案:
1.900; 2.三角形的稳定性; 3.135; 4.5; 5.∠B=60°;
6.74; 7. 22; 8.800; 9.十二边形; 10.6cm2;
11、选D。12、选B。13、选C;14、选A。15、选C; 16、选D。17、选B。18、选C。19、选D。20、选A。
21、
22、解:∠C=180°-∠ABC-∠A=180°-60°-70°=50°.
23、
解:AB=60米.
理由如下:∵在△ABC和△DEC中,
AC=DC
∠ACB=∠DCE
BC=EC.,
∴△ABC≌△DEC(SAS),
∴AB=DE=60(米),
则池塘的宽AB为60米
24、证明:延长AM到D,使MD=AM,连CD,
∵AM是BC边上的中线,∴BM=CM,
又AM=DM,∠AMB=∠CMD,
∴△ABM≌△DCM,∴AB=CD,
在△ACD中,则AD<AC+CD,
即2AM<AC+AB,
AM<(AB+AC).
25、因为BD是ABC的角平分线
所以∠ABD=∠DBC=ABC
因为∠A=∠C=∠ABC
所以∠A=∠ABD=∠DBC
因为∠BDC是∠A和∠ABD的外角
所以∠BDC=∠A+∠ABD=∠DBC+∠ABD=∠ABC=∠C
设∠A=x
则∠A+∠ABD+∠C=180=5x
x=36
所以∠A=36°
∠BDC=72°
26、证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠EAC,
在△BAD和△EAC中
AB=AC
∠BAD=∠EAC
AD=AE
∴BD=EC
27、证明:已知条件:AD∥BC,AE=CF,AD=BC,
求证结论:∠B=∠D.
证明:∵AE=CF,
∴AE+EF=CF+EF.
∴AF=CE.
∵AD∥BC,
∴∠A=∠C.
在△ADF和△CBE中
AD=BC,∠A=∠C,AF=CE,
∴△ADF≌△CBE.
∴∠B=∠D.
28、解:(1)根据三角形内角是180°可知:∠1+∠2=180°-∠A,∠B+∠C=180°-∠A,
∴∠1+∠2=∠B+∠C;
(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,
∴∠1+∠2=∠B+∠C;
当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°;
(3)如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°-300°=60°,
所以∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
第1题图
第4题图
第2题图
第3题图
第10题图
第8题图
第6题图
同课章节目录
