2022初一数学上册苏科版培优01数轴的应用 课件(共49张PPT)
文档属性
| 名称 | 2022初一数学上册苏科版培优01数轴的应用 课件(共49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 22:29:47 | ||
图片预览










文档简介
(共49张PPT)
数轴的应用
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
复习正数、负数、有理数
有理数的相关概念与实际应用
负数
小于0的数
大于0的数
0
非正非负
数
“+”可省
“—”不可省
提问:将我们认识的数按正负分可以怎么分呢?
正数
易错:一个未知数a,是正数、负数还是0?
讲解
引入
例题
练习
总结
有理数的相关概念与实际应用
提问:六非问题的口诀是什么?
口诀:见非写0,非后相反
试一试:
(1)非正数 (2)非负数
(3)非正整数 (4)非正分数
(5)非正有理数 (6)非负有理数
复习正数、负数、有理数
讲解
引入
例题
练习
总结
有理数的相关概念与实际应用
混合运算法则
1.先算乘方,再算乘除,最后算加减
2.如果有括号,先算小括号,
再算中括号,最后算大括号
3.同级运算,按从左往右的顺序进行
讲解
引入
例题
练习
总结
有理数的相关概念与实际应用
科学记数法
1、一般情况下,把大于10的数表示成a×10n(n为整数)的形式时,为了统一标准,规定了a的范围,(1≤ a<10),这种记数方法叫做科学记数法。
2、精确到以a的最后一个数在原数中的数位为准
3、有效数字就是指从左到右第一个非零数字开始算起,到精确到的数为止
讲解
引入
例题
练习
总结
有理数的相关概念与应用
3
讲解
引入
例题
练习
总结
有理数的相关概念与应用
3
讲解
引入
例题
练习
总结
科学记数法与近似数
4
讲解
引入
例题
练习
总结
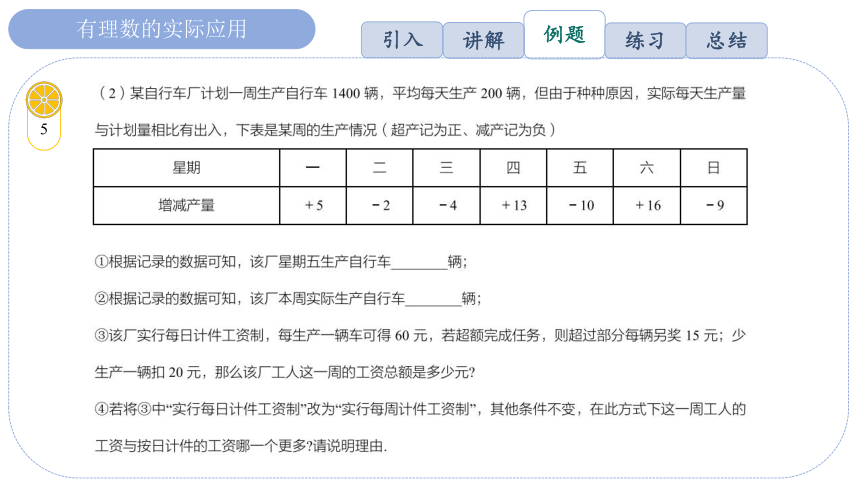
有理数的实际应用
4
讲解
引入
例题
练习
总结
有理数的实际应用
5
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
复习数轴
利用数轴比较大小
数轴三要素: (1)原点、
(2)正方向、
(3)单位长度
判断依据
提问:数轴的定义以及三要素?
讲解
引入
例题
练习
总结
复习数轴
利用数轴比较大小
提问:正方向向右的数轴上的数有什么规律?
(提示:正方向)
应用:比较大小(结合数轴比较大小)
总结:数轴上的点表示的数遵循“左小右大”的原则
(1)正数与正数比较
(2)正数与负数比较
(3)负数与负数比较
绝对值大的(离原点远)反而小
讲解
引入
例题
练习
总结
利用数轴比较大小
6
讲解
引入
例题
练习
总结
利用数轴比较大小
6
讲解
引入
例题
练习
总结
利用数轴比较大小
6
讲解
引入
例题
练习
总结
利用数轴比较大小
7
讲解
引入
例题
练习
总结
利用数轴比较大小
7
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
点的距离问题
方程思想计算点的位置
2
1
0
4
5
6
3
提问:距离A点2个单位长度的点表示的数是?
A
a
再次提问:距离A点2个单位长度的点表示的数是?
a+2或a-2
遇距离,两边找
讲解
引入
例题
练习
总结
方程思想计算点的位置
8
讲解
引入
例题
练习
总结
方程思想计算点的位置
8
讲解
引入
例题
练习
总结
方程思想计算点的位置
9
讲解
引入
例题
练习
总结
方程思想计算点的位置
9
讲解
引入
例题
练习
总结
方程思想计算点的位置
9
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
复习绝对值的代数意义
分类讨论思想计算距离
-1
-2
-3
1
2
3
0
提问:绝对值的代数意义是?(用数学语言表示)
讲解
引入
例题
练习
总结
复习绝对值的代数意义
分类讨论思想计算距离
提问:在数轴上表示点a的点和表示点b的点之间的距离怎么表示?(用数学语言表示)
注意 :左右两种情况需要分情况讨论
讲解
引入
例题
练习
总结
分类讨论思想计算距离
10
讲解
引入
例题
练习
总结
分类讨论思想计算距离
10
讲解
引入
例题
练习
总结
分类讨论思想计算距离
11
讲解
引入
例题
练习
总结
分类讨论思想计算距离
11
讲解
引入
例题
练习
总结
分类讨论思想计算距离
11
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
数轴上表示动点
数形结合
-1
-2
-3
1
2
3
0
提问:数轴上点A在原点以2个单位长度为速度向右进行运动,当时间为t时点A表示的数是?
A
2t
数轴上点A在原点以v为速度进行运动,当时间为t时点A表示的数是?
vt或-vt
数轴上点A在-5处以v为速度向右进行运动,当时间为t时点A表示的数是?
-5+vt
讲解
引入
例题
练习
总结
数轴上表示动点
数形结合
-1
-2
-3
1
2
3
0
提问:数轴上动点A在数字a处以v为速度向右进行运动,当时间为t时点A表示的数是?
A
a+vt
讲解
引入
例题
练习
总结
12
数形结合
讲解
引入
例题
练习
总结
12
数形结合
讲解
引入
例题
练习
总结
13
数形结合
讲解
引入
例题
练习
总结
13
数形结合
讲解
引入
例题
练习
总结
14
数形结合
讲解
引入
例题
练习
总结
14
数形结合
讲解
引入
例题
练习
总结
性质
1.菱形的性质
讲解
引入
例题
练习
总结
1.菱形的性质
66
讲解
引入
练习
例题
总结
1.菱形的性质
66
讲解
引入
总结
例题
练习
1.菱形的性质
明天见!
数轴的应用
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
复习正数、负数、有理数
有理数的相关概念与实际应用
负数
小于0的数
大于0的数
0
非正非负
数
“+”可省
“—”不可省
提问:将我们认识的数按正负分可以怎么分呢?
正数
易错:一个未知数a,是正数、负数还是0?
讲解
引入
例题
练习
总结
有理数的相关概念与实际应用
提问:六非问题的口诀是什么?
口诀:见非写0,非后相反
试一试:
(1)非正数 (2)非负数
(3)非正整数 (4)非正分数
(5)非正有理数 (6)非负有理数
复习正数、负数、有理数
讲解
引入
例题
练习
总结
有理数的相关概念与实际应用
混合运算法则
1.先算乘方,再算乘除,最后算加减
2.如果有括号,先算小括号,
再算中括号,最后算大括号
3.同级运算,按从左往右的顺序进行
讲解
引入
例题
练习
总结
有理数的相关概念与实际应用
科学记数法
1、一般情况下,把大于10的数表示成a×10n(n为整数)的形式时,为了统一标准,规定了a的范围,(1≤ a<10),这种记数方法叫做科学记数法。
2、精确到以a的最后一个数在原数中的数位为准
3、有效数字就是指从左到右第一个非零数字开始算起,到精确到的数为止
讲解
引入
例题
练习
总结
有理数的相关概念与应用
3
讲解
引入
例题
练习
总结
有理数的相关概念与应用
3
讲解
引入
例题
练习
总结
科学记数法与近似数
4
讲解
引入
例题
练习
总结
有理数的实际应用
4
讲解
引入
例题
练习
总结
有理数的实际应用
5
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
复习数轴
利用数轴比较大小
数轴三要素: (1)原点、
(2)正方向、
(3)单位长度
判断依据
提问:数轴的定义以及三要素?
讲解
引入
例题
练习
总结
复习数轴
利用数轴比较大小
提问:正方向向右的数轴上的数有什么规律?
(提示:正方向)
应用:比较大小(结合数轴比较大小)
总结:数轴上的点表示的数遵循“左小右大”的原则
(1)正数与正数比较
(2)正数与负数比较
(3)负数与负数比较
绝对值大的(离原点远)反而小
讲解
引入
例题
练习
总结
利用数轴比较大小
6
讲解
引入
例题
练习
总结
利用数轴比较大小
6
讲解
引入
例题
练习
总结
利用数轴比较大小
6
讲解
引入
例题
练习
总结
利用数轴比较大小
7
讲解
引入
例题
练习
总结
利用数轴比较大小
7
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
点的距离问题
方程思想计算点的位置
2
1
0
4
5
6
3
提问:距离A点2个单位长度的点表示的数是?
A
a
再次提问:距离A点2个单位长度的点表示的数是?
a+2或a-2
遇距离,两边找
讲解
引入
例题
练习
总结
方程思想计算点的位置
8
讲解
引入
例题
练习
总结
方程思想计算点的位置
8
讲解
引入
例题
练习
总结
方程思想计算点的位置
9
讲解
引入
例题
练习
总结
方程思想计算点的位置
9
讲解
引入
例题
练习
总结
方程思想计算点的位置
9
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
复习绝对值的代数意义
分类讨论思想计算距离
-1
-2
-3
1
2
3
0
提问:绝对值的代数意义是?(用数学语言表示)
讲解
引入
例题
练习
总结
复习绝对值的代数意义
分类讨论思想计算距离
提问:在数轴上表示点a的点和表示点b的点之间的距离怎么表示?(用数学语言表示)
注意 :左右两种情况需要分情况讨论
讲解
引入
例题
练习
总结
分类讨论思想计算距离
10
讲解
引入
例题
练习
总结
分类讨论思想计算距离
10
讲解
引入
例题
练习
总结
分类讨论思想计算距离
11
讲解
引入
例题
练习
总结
分类讨论思想计算距离
11
讲解
引入
例题
练习
总结
分类讨论思想计算距离
11
一、有理数的相关概念与实际应用
目录
1
2
3
专题一、利用数轴比较大小
专题二、方程思想计算点的位置
4
专题三、分类讨论思想计算距离
5
专题四、数形结合计算数轴上的动点
讲解
引入
例题
练习
总结
数轴上表示动点
数形结合
-1
-2
-3
1
2
3
0
提问:数轴上点A在原点以2个单位长度为速度向右进行运动,当时间为t时点A表示的数是?
A
2t
数轴上点A在原点以v为速度进行运动,当时间为t时点A表示的数是?
vt或-vt
数轴上点A在-5处以v为速度向右进行运动,当时间为t时点A表示的数是?
-5+vt
讲解
引入
例题
练习
总结
数轴上表示动点
数形结合
-1
-2
-3
1
2
3
0
提问:数轴上动点A在数字a处以v为速度向右进行运动,当时间为t时点A表示的数是?
A
a+vt
讲解
引入
例题
练习
总结
12
数形结合
讲解
引入
例题
练习
总结
12
数形结合
讲解
引入
例题
练习
总结
13
数形结合
讲解
引入
例题
练习
总结
13
数形结合
讲解
引入
例题
练习
总结
14
数形结合
讲解
引入
例题
练习
总结
14
数形结合
讲解
引入
例题
练习
总结
性质
1.菱形的性质
讲解
引入
例题
练习
总结
1.菱形的性质
66
讲解
引入
练习
例题
总结
1.菱形的性质
66
讲解
引入
总结
例题
练习
1.菱形的性质
明天见!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
