2022-2023学年人教版八年级数学上册《14.1.2 幂的乘方》 教学课件 (共18张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册《14.1.2 幂的乘方》 教学课件 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 15:42:28 | ||
图片预览






文档简介
(共18张PPT)
14.1.2 幂的乘方
1.掌握幂的乘方的运算性质,能用文字语言和符号语言正确地表述该性质;
2.能熟练地运用幂的乘方的运算性质进行运算;
3.经历幂的乘方的运算性质的推导过程,体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用;
4.通过类比学习,合作交流,培养学生的观察、发现、归纳、概括能力,使学生初步理解“特殊到一般再到特殊”的认知规律.
学习目标
幂的乘方
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
全班作答
同底数幂的乘法的运算性质是什么?
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
思考
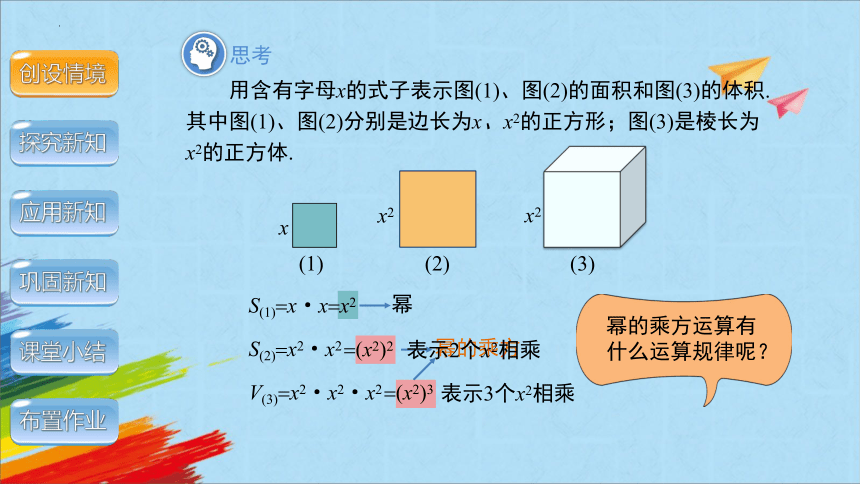
用含有字母x的式子表示图(1)、图(2)的面积和图(3)的体积.其中图(1)、图(2)分别是边长为x、x2的正方形;图(3)是棱长为x2的正方体.
(1)
(2)
(3)
x
x2
x2
S(1) x·x x2
S(2) x2·x2
V(3) x2·x2·x2
(x2)2
(x2)3
幂
幂的乘方
幂的乘方运算有什么运算规律呢?
表示2个x2相乘
表示3个x2相乘
根据乘方的意义及同底数幂的乘法填空:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(32)3 ( ) ( ) ( ) 3( ) 3( ) ;
(2)(a2)3 ( )·( )·( ) a( ) a( ) ;
(3)(am)3 ( )·( )·( ) a( ) a( )(m是正整数).
6
6
3m
a2
a2
a2
am
am
am
32
32
32
(32)3表示3个32相乘
(a2)3表示3个a2相乘
(am)3表示3个am相乘
2 2 2
2 2 2
m m m
观察计算结果,你发现了什么规律?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(32)3 32 32 32 3(2 2 2) 3( 6 );
(2)(a2)3 a2·a2·a2 a(2 2 2) a( 6 );
(3)(am)3 am·am·am a(m m m) a( 3m )(m是正整数).
3( 2 3 );
a( 2 3 );
1.底数不变;
2.指数相加.
1.结果的底数与原来的底数相同;
2.结果的指数等于原来两个指数的积.
a( 3·m )(m是正整数).
你能用式子表示刚刚发现的规律吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
猜想
n个am
n个m
幂的乘方:
幂的乘方,底数不变,指数相乘.
(m,n都是正整数).
乘方的意义
同底数幂的乘法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
(m, n,p都是正整数)
是否依旧满足底数不变,指数相乘呢?
满足
(3) (am)2
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) (x4)3.
(2) (a4)4
解: (1) (103)5
103 5
1015.
(4) (x4)3
a4 4
a16.
am 2
a2m.
x4 3
x12.
(m,n都是正整数).
幂的乘方,底数不变,指数相乘.
同底数幂相乘,底数不变,指数相加.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
判断下列计算是否正确:
(1) a3·a5 a15; (2) (a4)3 a7.
同底数幂的乘法
幂的乘方
a8
a12
相
同
点
不
同
点
符号表示
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 计算:
(1) [(a2)3]4; (2) [(a b)3]2; (3) (103)m n.
解:(1) [(a2)3]4
a2 3 4
a24
(2) [(a b)3]2
(a b)3 2
(a b)6
(am)n amn中的底数a不仅可以代表数、单项式,还可以代表多项式等.
(3) (103)m n
103(m n)
(am)n amn中的指数m,n也可以代表多项式.
【选讲】
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例3 计算:
(1) (a4)3·a6 a18 ; (2) ( x3)2· ( x2)3 (x4)3.
混合运算顺序:
幂的乘方→同底数幂的乘法→加减法
解:(1) 原式 a4 3·a6 a18
a12·a6 a18
a18 a18
2a18
(2) 原式 x6·( x6) x12
x12 x12
2x12
( x3)·( x3)
( x2)·( x2)·( x2)
【选讲】
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
1.口答:
(1)(23)5 . (2)(a3)4 .
(3)[( 2)3]2 . (4) (a3)4 .
(5)x2·x5 . (6)(3n)3 .
抢答
215
a12
26
a12
x7
33n
2.下列计算结果是a9的是( ).
A. (a3)6 B. a3 a6 C. a9 a9 D. a3·a6
D
a18
2a9
a9
不能继续运算
3.计算:
(1)(a3)4·a5 (2)(x2)n (xn)2
(3)x4·x5·( x7) (x8)2 (4)2(a3)4 a4(a4)2 a5a7
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
解:原式 a12·a5
a17
解:原式 x2n x2n
0
解:原式 x16 x16
2x16
解:原式 2a12 a4·a8 a12
2a12 a12 a12
4a12
带 的为选做题
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
4.填空:
(1) 若(a3)x a15,则x .
(2)若ax 5,ay 6 ,则ax y ,a2x .
5
30
5.若10α 2,10β 3,求102α 3β的值.
解:102α 3β
102α·103β
(10α)2·(10β)3
22 33
108.
25
带 的为选做题
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
混合运算顺序:
幂的乘方→同底数幂的乘法→加减运算
幂的乘方
幂的乘方:
(m,n都是正整数).
布置作业
教科书第97页练习题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
14.1.2 幂的乘方
1.掌握幂的乘方的运算性质,能用文字语言和符号语言正确地表述该性质;
2.能熟练地运用幂的乘方的运算性质进行运算;
3.经历幂的乘方的运算性质的推导过程,体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用;
4.通过类比学习,合作交流,培养学生的观察、发现、归纳、概括能力,使学生初步理解“特殊到一般再到特殊”的认知规律.
学习目标
幂的乘方
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
全班作答
同底数幂的乘法的运算性质是什么?
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
思考
用含有字母x的式子表示图(1)、图(2)的面积和图(3)的体积.其中图(1)、图(2)分别是边长为x、x2的正方形;图(3)是棱长为x2的正方体.
(1)
(2)
(3)
x
x2
x2
S(1) x·x x2
S(2) x2·x2
V(3) x2·x2·x2
(x2)2
(x2)3
幂
幂的乘方
幂的乘方运算有什么运算规律呢?
表示2个x2相乘
表示3个x2相乘
根据乘方的意义及同底数幂的乘法填空:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(32)3 ( ) ( ) ( ) 3( ) 3( ) ;
(2)(a2)3 ( )·( )·( ) a( ) a( ) ;
(3)(am)3 ( )·( )·( ) a( ) a( )(m是正整数).
6
6
3m
a2
a2
a2
am
am
am
32
32
32
(32)3表示3个32相乘
(a2)3表示3个a2相乘
(am)3表示3个am相乘
2 2 2
2 2 2
m m m
观察计算结果,你发现了什么规律?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(32)3 32 32 32 3(2 2 2) 3( 6 );
(2)(a2)3 a2·a2·a2 a(2 2 2) a( 6 );
(3)(am)3 am·am·am a(m m m) a( 3m )(m是正整数).
3( 2 3 );
a( 2 3 );
1.底数不变;
2.指数相加.
1.结果的底数与原来的底数相同;
2.结果的指数等于原来两个指数的积.
a( 3·m )(m是正整数).
你能用式子表示刚刚发现的规律吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
猜想
n个am
n个m
幂的乘方:
幂的乘方,底数不变,指数相乘.
(m,n都是正整数).
乘方的意义
同底数幂的乘法
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
(m, n,p都是正整数)
是否依旧满足底数不变,指数相乘呢?
满足
(3) (am)2
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 计算:
(1) (103)5; (2) (a4)4; (3) (am)2; (4) (x4)3.
(2) (a4)4
解: (1) (103)5
103 5
1015.
(4) (x4)3
a4 4
a16.
am 2
a2m.
x4 3
x12.
(m,n都是正整数).
幂的乘方,底数不变,指数相乘.
同底数幂相乘,底数不变,指数相加.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
判断下列计算是否正确:
(1) a3·a5 a15; (2) (a4)3 a7.
同底数幂的乘法
幂的乘方
a8
a12
相
同
点
不
同
点
符号表示
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 计算:
(1) [(a2)3]4; (2) [(a b)3]2; (3) (103)m n.
解:(1) [(a2)3]4
a2 3 4
a24
(2) [(a b)3]2
(a b)3 2
(a b)6
(am)n amn中的底数a不仅可以代表数、单项式,还可以代表多项式等.
(3) (103)m n
103(m n)
(am)n amn中的指数m,n也可以代表多项式.
【选讲】
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例3 计算:
(1) (a4)3·a6 a18 ; (2) ( x3)2· ( x2)3 (x4)3.
混合运算顺序:
幂的乘方→同底数幂的乘法→加减法
解:(1) 原式 a4 3·a6 a18
a12·a6 a18
a18 a18
2a18
(2) 原式 x6·( x6) x12
x12 x12
2x12
( x3)·( x3)
( x2)·( x2)·( x2)
【选讲】
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
1.口答:
(1)(23)5 . (2)(a3)4 .
(3)[( 2)3]2 . (4) (a3)4 .
(5)x2·x5 . (6)(3n)3 .
抢答
215
a12
26
a12
x7
33n
2.下列计算结果是a9的是( ).
A. (a3)6 B. a3 a6 C. a9 a9 D. a3·a6
D
a18
2a9
a9
不能继续运算
3.计算:
(1)(a3)4·a5 (2)(x2)n (xn)2
(3)x4·x5·( x7) (x8)2 (4)2(a3)4 a4(a4)2 a5a7
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
解:原式 a12·a5
a17
解:原式 x2n x2n
0
解:原式 x16 x16
2x16
解:原式 2a12 a4·a8 a12
2a12 a12 a12
4a12
带 的为选做题
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
4.填空:
(1) 若(a3)x a15,则x .
(2)若ax 5,ay 6 ,则ax y ,a2x .
5
30
5.若10α 2,10β 3,求102α 3β的值.
解:102α 3β
102α·103β
(10α)2·(10β)3
22 33
108.
25
带 的为选做题
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
混合运算顺序:
幂的乘方→同底数幂的乘法→加减运算
幂的乘方
幂的乘方:
(m,n都是正整数).
布置作业
教科书第97页练习题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
