冀教版七年级数学下册6.2 二元一次方程组的解法(2) 课件(共19张PPT)
文档属性
| 名称 | 冀教版七年级数学下册6.2 二元一次方程组的解法(2) 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 928.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 15:50:26 | ||
图片预览






文档简介
(共19张PPT)
6.2 二元一次方程组的解法
第2课时 代入消元法(2)
第六章 二元一次方程组
解方程组
②
①
解:方程①可变形为
x=10-y. ③
将③代入②中,得
10-y-2y=4.
解这个方程,得
y=2.
将y=2代入③中,得
x=8.
所以原方程组的解为
步骤
变 形
代入
求 解
代入求解
写解
知识回顾
学习目标
6.2 第2课时 代入消元法(2)
1.会用代入消元法解复杂系数的二元一次方程组。(重点)
2.体会转化思想在解二元一次方程组中的应用,会根据题目特点灵活解二元一次方程组.(难点)
自学指导
自主学习教材8-9页,并完成下列问题(3分钟)
1.认真阅读例2、例3,注意解题的格式、方法和步骤。
2. 阅读“大家谈谈”,总结归纳代入消元法的一般步骤。
请注意:坐姿端正,书写整齐
请大家自主完成课本10页练习第2题、习题第1题(2)
随堂训练(5分钟)
例1 解方程组
②
①
解:由方程①,得
③
将③代入②,整理,得
解方程,得
将 代入③,得
所以,原方程的解为
例题讲解
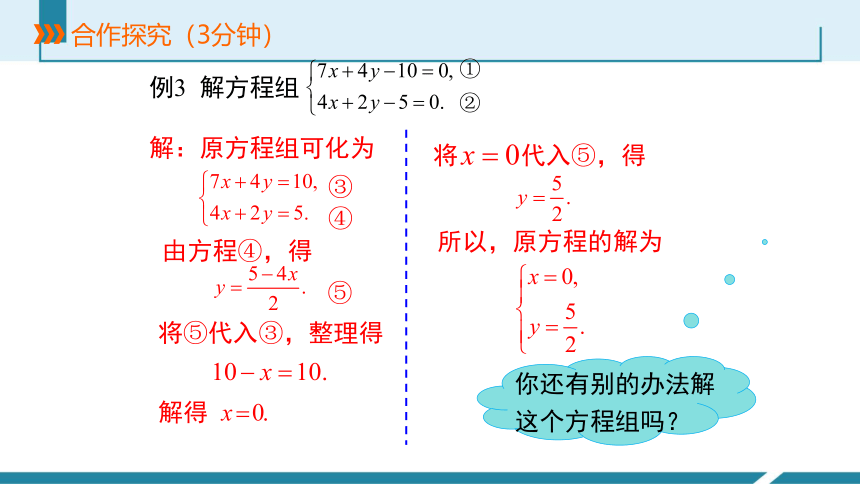
例3 解方程组
②
①
解:原方程组可化为
③
④
由方程④,得
⑤
将⑤代入③,整理得
解得
将 代入⑤,得
所以,原方程的解为
你还有别的办法解这个方程组吗?
合作探究(3分钟)
解方程组
②
①
解:原方程组可化为
③
④
由方程④,得
⑤
将⑤代入③,得
⑤
解这个一元一次方程,得
将 代入⑤,得
所以,原方程的解为
合作探究
6.2 第2课时 代入消元法(2)
合作探究(3分钟)
6.2 第2课时 代入消元法(2)
(2) 当方程组中的二元一次方程为ax+by+c=k的形式,一般先将方程化为ax+by=k-c 的形式.
(3)当相同未知数的系数成倍数关系时,我们常用整体代入法会使解法更加快捷简便!
获取新知
绝对值较小
巩固练习
②
①
②
①
1.解方程组
1.解方程组
②
①
解:(1)由方程②,得
③
将③代入①,得
④
解方程④,得
将 代入③,得
所以,原方程的解为
巩固练习
解:(2)原方程组可化为
③
④
②
①
由方程③,得
⑤
将⑤代入④,整理,得
解得
将 代入⑤,得
所以,原方程的解为
巩固练习
2.已知 和 都是方程mx+ny=7的解,求6m+2n的值.
随堂演练
3.已知方程组 的解x与y的值相等,则k=___ .
解析:由题意可知x与y的值相等,即x=y.可将其代入方程2x+3y=5中,解得x=1.而后将x=y代入4x-3y=k中,整理,得 x=k.即k=x=1.
4.若 ,则x=___ ,y=__.
1
解析:根据绝对值的非负性可列出方程组
解这个方程组,得
1
-1
随堂演练
二元一次方程组
一元一次方程
转化
代入 消元法
变形
代入消元
回代求值
写解
整体代入
课堂小结
求解
全品第4页:
必做:1-7题
选做:8-9题
下课上交,看谁完成的又对又快!
堂清作业
6.2 二元一次方程组的解法
第2课时 代入消元法(2)
第六章 二元一次方程组
解方程组
②
①
解:方程①可变形为
x=10-y. ③
将③代入②中,得
10-y-2y=4.
解这个方程,得
y=2.
将y=2代入③中,得
x=8.
所以原方程组的解为
步骤
变 形
代入
求 解
代入求解
写解
知识回顾
学习目标
6.2 第2课时 代入消元法(2)
1.会用代入消元法解复杂系数的二元一次方程组。(重点)
2.体会转化思想在解二元一次方程组中的应用,会根据题目特点灵活解二元一次方程组.(难点)
自学指导
自主学习教材8-9页,并完成下列问题(3分钟)
1.认真阅读例2、例3,注意解题的格式、方法和步骤。
2. 阅读“大家谈谈”,总结归纳代入消元法的一般步骤。
请注意:坐姿端正,书写整齐
请大家自主完成课本10页练习第2题、习题第1题(2)
随堂训练(5分钟)
例1 解方程组
②
①
解:由方程①,得
③
将③代入②,整理,得
解方程,得
将 代入③,得
所以,原方程的解为
例题讲解
例3 解方程组
②
①
解:原方程组可化为
③
④
由方程④,得
⑤
将⑤代入③,整理得
解得
将 代入⑤,得
所以,原方程的解为
你还有别的办法解这个方程组吗?
合作探究(3分钟)
解方程组
②
①
解:原方程组可化为
③
④
由方程④,得
⑤
将⑤代入③,得
⑤
解这个一元一次方程,得
将 代入⑤,得
所以,原方程的解为
合作探究
6.2 第2课时 代入消元法(2)
合作探究(3分钟)
6.2 第2课时 代入消元法(2)
(2) 当方程组中的二元一次方程为ax+by+c=k的形式,一般先将方程化为ax+by=k-c 的形式.
(3)当相同未知数的系数成倍数关系时,我们常用整体代入法会使解法更加快捷简便!
获取新知
绝对值较小
巩固练习
②
①
②
①
1.解方程组
1.解方程组
②
①
解:(1)由方程②,得
③
将③代入①,得
④
解方程④,得
将 代入③,得
所以,原方程的解为
巩固练习
解:(2)原方程组可化为
③
④
②
①
由方程③,得
⑤
将⑤代入④,整理,得
解得
将 代入⑤,得
所以,原方程的解为
巩固练习
2.已知 和 都是方程mx+ny=7的解,求6m+2n的值.
随堂演练
3.已知方程组 的解x与y的值相等,则k=___ .
解析:由题意可知x与y的值相等,即x=y.可将其代入方程2x+3y=5中,解得x=1.而后将x=y代入4x-3y=k中,整理,得 x=k.即k=x=1.
4.若 ,则x=___ ,y=__.
1
解析:根据绝对值的非负性可列出方程组
解这个方程组,得
1
-1
随堂演练
二元一次方程组
一元一次方程
转化
代入 消元法
变形
代入消元
回代求值
写解
整体代入
课堂小结
求解
全品第4页:
必做:1-7题
选做:8-9题
下课上交,看谁完成的又对又快!
堂清作业
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
