2022-2023学年人教版八年级数学上册14.1.3积的乘方 课件(共21张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册14.1.3积的乘方 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 15:51:54 | ||
图片预览






文档简介
(共21张PPT)
14.1.3 积的乘方
1.掌握积的乘方的运算性质,能用文字语言和符号语言正确地表述该性质;
2.能熟练地运用积的乘方的运算性质进行运算;
3.经历积的乘方的运算性质的推导过程,体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用;
4.通过类比学习,合作交流,培养学生的观察、发现、归纳、概括能力,使学生初步理解“特殊到一般再到特殊”的认知规律.
学习目标
积的乘方
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
全班作答
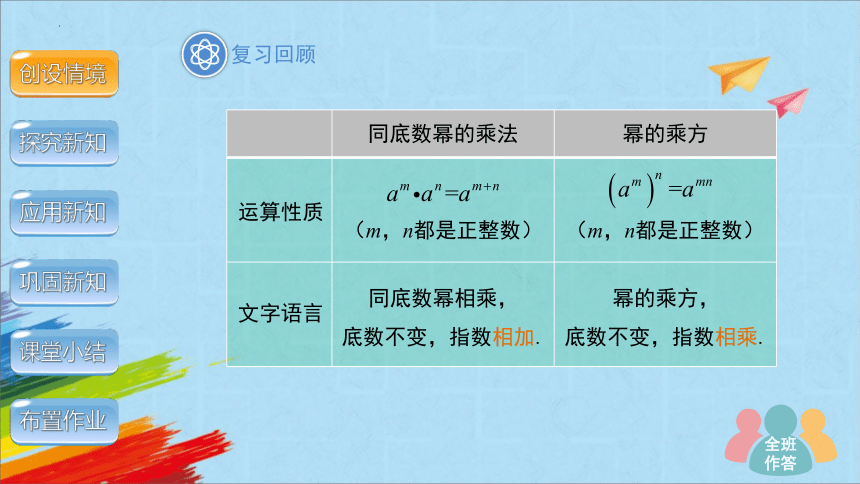
同底数幂的乘法 幂的乘方
运算性质
文字语言
(m,n都是正整数)
(m,n都是正整数)
同底数幂相乘,
底数不变,指数相加.
幂的乘方,
底数不变,指数相乘.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
思考
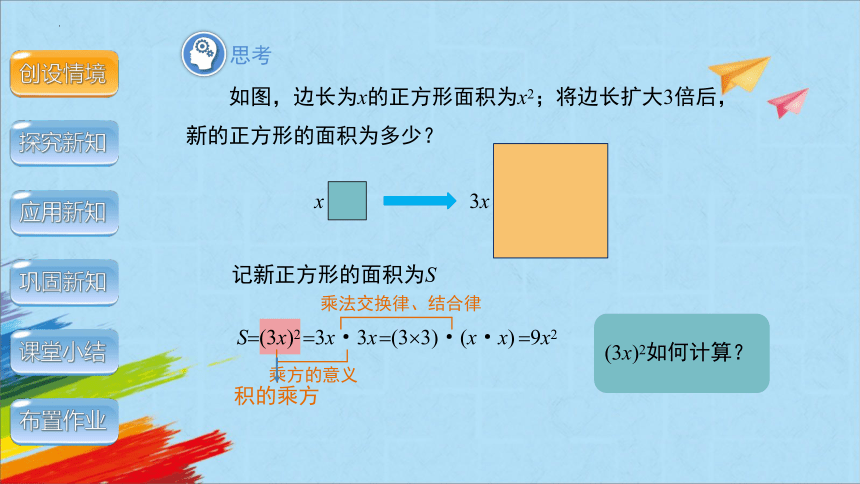
如图,边长为x的正方形面积为x2;将边长扩大3倍后,新的正方形的面积为多少?
S (3x)2
x
3x
记新正方形的面积为S
3x·3x
(3 3)·(x·x)
9x2
乘方的意义
乘法交换律、结合律
积的乘方
积的乘方有什么运算规律呢?
(3x)2如何计算?
填空:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(3x)2=3x·3x=(3 3)·(x·x)=3( )x( );
(2)(ab)2 a( )b( ) ;
(3)(ab)3 a( )b( ) .
(ab)·(ab)·(ab)
(ab)·(ab)
(a·a)·(b·b)
(a·a·a)·(b·b·b)
2
2
2
2
3
3
运算过程用到哪些运算律?
乘法交换律、结合律
观察计算前后,你能发现什么规律?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(3x)2=3x·3x=(3 3)·(x·x)=3( )x( );
2
2
(2)(ab)2 a( )b( ) ;
(ab)·(ab)
(a·a)·(b·b)
2
2
(3)(ab)3 a( )b( ) .
(ab)·(ab)·(ab)
(a·a·a)·(b·b·b)
3
3
变;
2.指数相加.
1.左边都是积的乘方;
2.结果中,把积的每一个因式分别乘方,再把所得的幂相乘.
你能用式子表示刚刚发现的规律吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
猜想
(ab)n anbn
(ab)n
(ab)·(ab)·…·(ab)
n个ab
a·a·…·a
n个a
·b·b·…·b
n个b
anbn
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
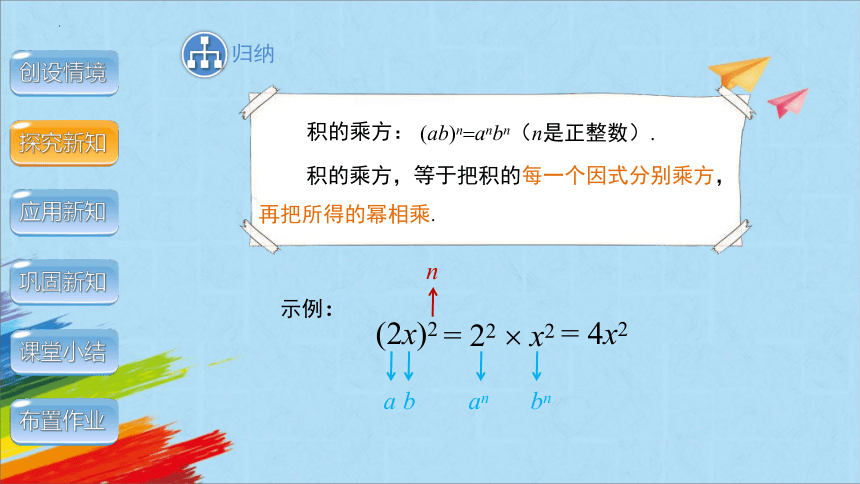
积的乘方:
(ab)n anbn(n是正整数).
归纳
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
n
a
b
an
bn
(2x)2
示例:
= 22 x2
= 4x2
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
积的乘方:
(ab)n anbn(n是正整数).
归纳
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
1.积的乘方的性质也适用于三个及三个以上因式的积的乘方,即(abc)n=anbncn(n为正整数).
2.在积的乘方中,底数中的a,b、指数n可以是单项式,也可以是多项式.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 计算:
(1) (2a)3 ; (2) ( 5b)3 ; (3) (xy2)2 ; (4) ( 2x3)4 .
(ab)n anbn(n是正整数).
解:(1) (2a)3
(2) ( 5b)3
(3) (xy2)2
(4) ( 2x3)4
23·a3
( 5)3·b3
x2·(y2)2
( 2)4·(x3)4
8a3 ;
125b3 ;
x2y4 ;
16x12 .
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
判断下列计算是否正确:
(1) (ab2)3 ab6;
(2) ( 2a2)2 4a4;
(3) ( x2y)3 x6y3.
(ab2)3 a3·(b2)3 a3b6
( 2a2)2 ( 2)2·(a2)2 4a4
( x2y)3 ( 1)3·(x2)3·y3 x6y3
1.积的乘方,要把积的每一个因式分别乘方,不要漏掉任何一项;
2.当底数中含有“ ”时,应将其视为“ 1”,作为一个因式参与运算.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 计算:
(1) ; (2) 0.255 46.
(ab)n anbn(n是正整数).
解:(1)
(2) 0.255 46
逆用
0.255 45 4
(0.25 4)5 4
4
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例3 计算:2(x3)2·x3 (3x3)3 (5x)2·x7.
解:
2(x3)2·x3 (3x3)3 (5x)2·x7
2(x3)2·x3 33·(x3)3 52x2·x7
2x6·x3 27x9 25x2·x7
2x9 27x9 25x9
0
积的乘方
↓
幂的乘方
↓
同底数幂的乘法
↓
加减法
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
抢答
1. 下列运算正确的是( )
A. a2·a3 a6
B. (3a)3 9a3
C. 3a 2a 1
D. ( 2a2)3 8a6
D
a2·a3 a2 3 a5
(3a)3 33·a3 27a3
3a 2a (3 2)a a
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
解:(1) ( 3 102)3 ( 3)3 (102)3
(3) ( a2b3)3 ( 1)3·(a2)3·(b3)3
2.计算:
(1) ( 3 102)3 ; (2) [( a3)2]2 ; (3) ( a2b3)3 .
另解:
(2) [( a3)2]2
( a6)2
( )2·(a6)2
a12 ;
[( a3)2]2 ( a3)4 ( )4·(a3)4 a12
27 106
2.7 107 ;
a6b9 .
另解
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
3.计算:
(1) (2) 0.04999 [( 5)999]2
解:(1) 原式
(2) 原式 (0.22)999 [( 5)999]2
原式 0.04999 ( 5)999 ( 5)999
0.21998 ( 5)1998
[0.2 ( 5)]1998
1
[0.04 ( 5) ( 5)]999
1
原式 0.04999 [( 5)2]999
[0.04 ( 5)2]999
1
带 的为选做题
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
4.计算:
(1) (2a2)3 7a6 a2·a4 (2) ( x3y)4 2(x6y2)2
解:(1) 原式 23(a2)3 7a6 a2·a4
(2) 原式 ( 1)4(x3)4y4 2(x6)2(y2)2
8a6 7a6 a6
2a6
x12y4 2x12y4
3x12y4
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
5.如果(anbmb)3 a9b15,求m, n的值.
解:(anbmb)3 (an)3·(bm)3·b3
a3n·b3m·b3
a3n·b3m 3
∵(anbmb)3 a9b15
∴3n 9,3m 3 15
解得: m 4,n 3.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
注意事项:
1.积的乘方,要把积的每一个因式分别乘方,不要漏掉任何一项;
2.当底数中含有“ ”时,应将其视为“ 1”,作为一个因式参与运算.
积的乘方
积的乘方:
(ab)n anbn(n是正整数).
布置作业
教科书第98页练习题;
习题14.1第2题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
14.1.3 积的乘方
1.掌握积的乘方的运算性质,能用文字语言和符号语言正确地表述该性质;
2.能熟练地运用积的乘方的运算性质进行运算;
3.经历积的乘方的运算性质的推导过程,体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用;
4.通过类比学习,合作交流,培养学生的观察、发现、归纳、概括能力,使学生初步理解“特殊到一般再到特殊”的认知规律.
学习目标
积的乘方
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
复习回顾
全班作答
同底数幂的乘法 幂的乘方
运算性质
文字语言
(m,n都是正整数)
(m,n都是正整数)
同底数幂相乘,
底数不变,指数相加.
幂的乘方,
底数不变,指数相乘.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
思考
如图,边长为x的正方形面积为x2;将边长扩大3倍后,新的正方形的面积为多少?
S (3x)2
x
3x
记新正方形的面积为S
3x·3x
(3 3)·(x·x)
9x2
乘方的意义
乘法交换律、结合律
积的乘方
积的乘方有什么运算规律呢?
(3x)2如何计算?
填空:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(3x)2=3x·3x=(3 3)·(x·x)=3( )x( );
(2)(ab)2 a( )b( ) ;
(3)(ab)3 a( )b( ) .
(ab)·(ab)·(ab)
(ab)·(ab)
(a·a)·(b·b)
(a·a·a)·(b·b·b)
2
2
2
2
3
3
运算过程用到哪些运算律?
乘法交换律、结合律
观察计算前后,你能发现什么规律?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
(1)(3x)2=3x·3x=(3 3)·(x·x)=3( )x( );
2
2
(2)(ab)2 a( )b( ) ;
(ab)·(ab)
(a·a)·(b·b)
2
2
(3)(ab)3 a( )b( ) .
(ab)·(ab)·(ab)
(a·a·a)·(b·b·b)
3
3
变;
2.指数相加.
1.左边都是积的乘方;
2.结果中,把积的每一个因式分别乘方,再把所得的幂相乘.
你能用式子表示刚刚发现的规律吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
猜想
(ab)n anbn
(ab)n
(ab)·(ab)·…·(ab)
n个ab
a·a·…·a
n个a
·b·b·…·b
n个b
anbn
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
积的乘方:
(ab)n anbn(n是正整数).
归纳
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
n
a
b
an
bn
(2x)2
示例:
= 22 x2
= 4x2
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
积的乘方:
(ab)n anbn(n是正整数).
归纳
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
1.积的乘方的性质也适用于三个及三个以上因式的积的乘方,即(abc)n=anbncn(n为正整数).
2.在积的乘方中,底数中的a,b、指数n可以是单项式,也可以是多项式.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 计算:
(1) (2a)3 ; (2) ( 5b)3 ; (3) (xy2)2 ; (4) ( 2x3)4 .
(ab)n anbn(n是正整数).
解:(1) (2a)3
(2) ( 5b)3
(3) (xy2)2
(4) ( 2x3)4
23·a3
( 5)3·b3
x2·(y2)2
( 2)4·(x3)4
8a3 ;
125b3 ;
x2y4 ;
16x12 .
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
判断下列计算是否正确:
(1) (ab2)3 ab6;
(2) ( 2a2)2 4a4;
(3) ( x2y)3 x6y3.
(ab2)3 a3·(b2)3 a3b6
( 2a2)2 ( 2)2·(a2)2 4a4
( x2y)3 ( 1)3·(x2)3·y3 x6y3
1.积的乘方,要把积的每一个因式分别乘方,不要漏掉任何一项;
2.当底数中含有“ ”时,应将其视为“ 1”,作为一个因式参与运算.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 计算:
(1) ; (2) 0.255 46.
(ab)n anbn(n是正整数).
解:(1)
(2) 0.255 46
逆用
0.255 45 4
(0.25 4)5 4
4
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例3 计算:2(x3)2·x3 (3x3)3 (5x)2·x7.
解:
2(x3)2·x3 (3x3)3 (5x)2·x7
2(x3)2·x3 33·(x3)3 52x2·x7
2x6·x3 27x9 25x2·x7
2x9 27x9 25x9
0
积的乘方
↓
幂的乘方
↓
同底数幂的乘法
↓
加减法
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
抢答
1. 下列运算正确的是( )
A. a2·a3 a6
B. (3a)3 9a3
C. 3a 2a 1
D. ( 2a2)3 8a6
D
a2·a3 a2 3 a5
(3a)3 33·a3 27a3
3a 2a (3 2)a a
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
解:(1) ( 3 102)3 ( 3)3 (102)3
(3) ( a2b3)3 ( 1)3·(a2)3·(b3)3
2.计算:
(1) ( 3 102)3 ; (2) [( a3)2]2 ; (3) ( a2b3)3 .
另解:
(2) [( a3)2]2
( a6)2
( )2·(a6)2
a12 ;
[( a3)2]2 ( a3)4 ( )4·(a3)4 a12
27 106
2.7 107 ;
a6b9 .
另解
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
3.计算:
(1) (2) 0.04999 [( 5)999]2
解:(1) 原式
(2) 原式 (0.22)999 [( 5)999]2
原式 0.04999 ( 5)999 ( 5)999
0.21998 ( 5)1998
[0.2 ( 5)]1998
1
[0.04 ( 5) ( 5)]999
1
原式 0.04999 [( 5)2]999
[0.04 ( 5)2]999
1
带 的为选做题
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
4.计算:
(1) (2a2)3 7a6 a2·a4 (2) ( x3y)4 2(x6y2)2
解:(1) 原式 23(a2)3 7a6 a2·a4
(2) 原式 ( 1)4(x3)4y4 2(x6)2(y2)2
8a6 7a6 a6
2a6
x12y4 2x12y4
3x12y4
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
5.如果(anbmb)3 a9b15,求m, n的值.
解:(anbmb)3 (an)3·(bm)3·b3
a3n·b3m·b3
a3n·b3m 3
∵(anbmb)3 a9b15
∴3n 9,3m 3 15
解得: m 4,n 3.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
注意事项:
1.积的乘方,要把积的每一个因式分别乘方,不要漏掉任何一项;
2.当底数中含有“ ”时,应将其视为“ 1”,作为一个因式参与运算.
积的乘方
积的乘方:
(ab)n anbn(n是正整数).
布置作业
教科书第98页练习题;
习题14.1第2题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
