2022-2023 学年人教版八年级数学上册15.2.1分式的乘除(1)课件(共28张PPT)
文档属性
| 名称 | 2022-2023 学年人教版八年级数学上册15.2.1分式的乘除(1)课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 15:53:31 | ||
图片预览





文档简介
(共28张PPT)
15.2.1 分式的乘除
第1课时
学习目标
1.理解并掌握分式的乘除法法则;
2.运用法则进行运算,能解决一些与分式有关的实际问题;
3.经历探索分式的乘除运算法则的过程,培养学生类比的思想方法,提高分析问题,解决问题的能力;
4.通过联系实际探究分式乘除运算法则的过程,培养学生与他人的合作意识.
分式的乘除
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
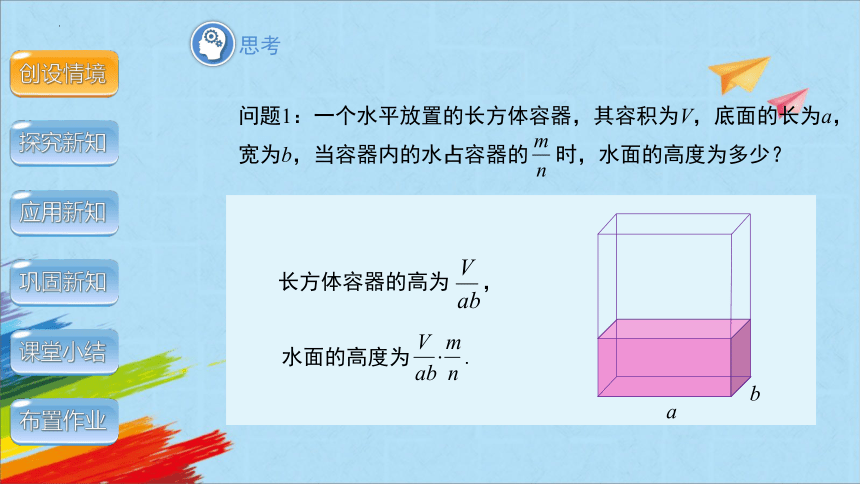
问题1:一个水平放置的长方体容器,其容积为V,底面的长为a,宽为b,当容器内的水占容器的 时,水面的高度为多少?
长方体容器的高为 ,
水面的高度为 .
b
a
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题2:大拖拉机 m 天耕地 a hm2,小拖拉机 n 天耕地 b hm2,大拖拉机的工作效率是小拖拉机工作效率的多少倍?
大拖拉机的工作效率是 hm2/天;
小拖拉机的工作效率是 hm2/天;
大拖拉机的工作效率是小拖拉机工作效率的 倍.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
问题1:一个水平放置的长方体容器,其容积为V,底面的长为a,宽为b,当容器内的水占容器的 时,水面的高度为 .
问题2:大拖拉机 m 天耕地 a hm2,小拖拉机 n 天耕地 b hm2,大拖拉机的工作效率是小拖拉机工作效率的 倍.
从上面的问题可知,为讨论数量关系,有时需要进行分式的乘除运算.
那么分式的乘除运算该怎么计算呢?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
还记得分数的乘除法运算吗?
分数的乘法法则:
分数乘以分数,用分子相乘的积做分子,分母相乘的积做分母.
分数的除法法则:
分数除以分数,等于
被除数乘以除数的倒数.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
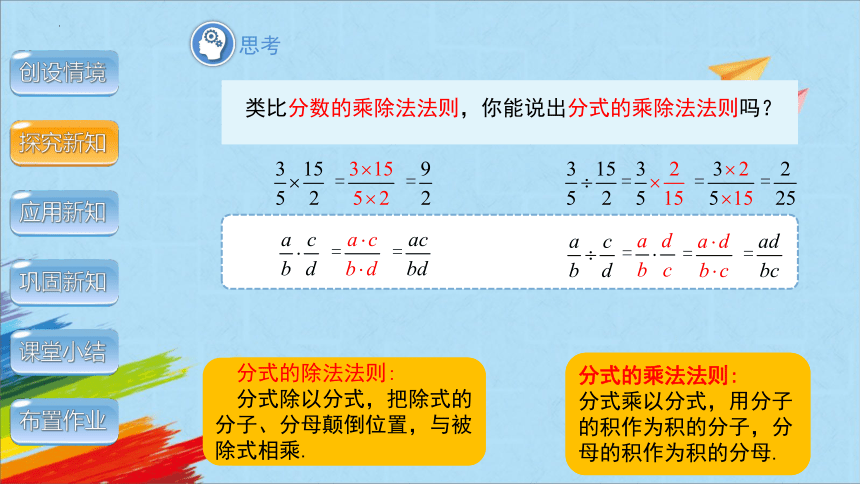
类比分数的乘除法法则,你能说出分式的乘除法法则吗?
分数的乘法法则:
分数乘以分数,用分子相乘的积做分子,分母相乘的积做分母.
分数的除法法则:
分数除以分数,等于
被除数乘以除数的倒数.
分式的除法法则:
分式除以分式,把除式的分子、分母颠倒位置,与被除式相乘.
分式的乘法法则:
分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
思考
分式的除法法则
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
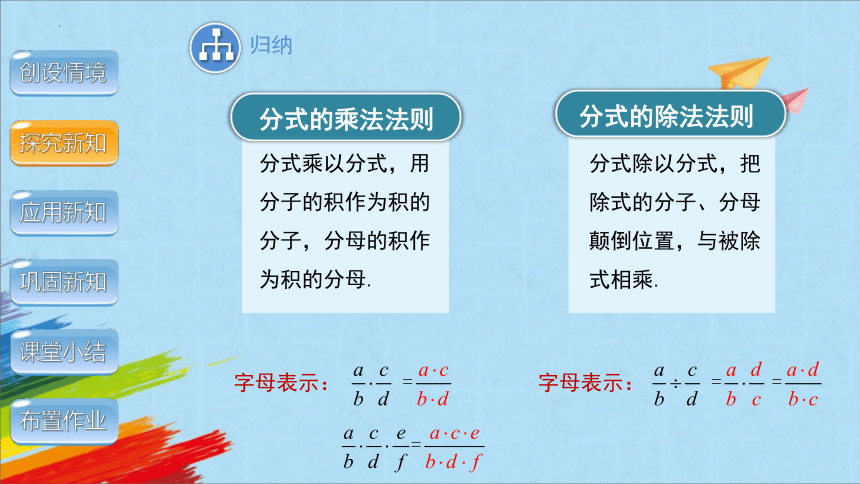
分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
分式的乘法法则
分式除以分式,把除式的分子、分母颠倒位置,与被除式相乘.
字母表示:
字母表示:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
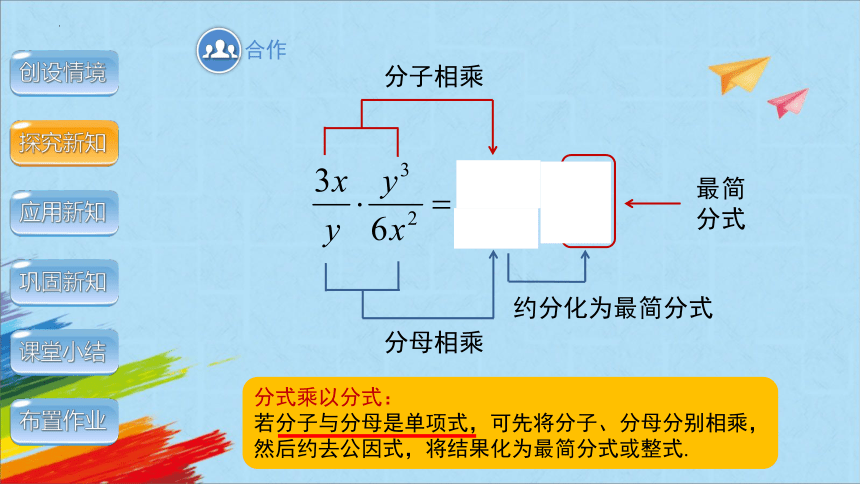
分母相乘
分子相乘
约分化为最简分式
最简
分式
分式乘以分式:
若分子与分母是单项式,可先将分子、分母分别相乘,然后约去公因式,将结果化为最简分式或整式.
合作
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作
分式和分式相乘:
若分子(分母)是多项式,则先将分子(分母)分解因式,再相乘,且其结果要化简为最简分式或整式.
因式分解
约分化为最简分式
最简
分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分母相乘
分子相乘
约分化为最简分式
整式
整式的分母看成1
合作
分式和整式相乘:
只需要把整式(看作分母为1的式子)与分式的分子相乘,用其结果作为积的分子,分母不变;当整式是多项式时,同样要先分解因式.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式与分式相乘:
①若分子与分母是单项式,可先将分子、分母分别相乘,然后约去公因式,将结果化为最简分式或整式;
②若分子、分母是多项式,则先将分子、分母分解因式,再相乘,且其结果要化简为最简分式或整式.
分式和整式相乘:
只需要把整式(看作分母为1的式子)与分式的分子相乘,用其结果作为积的分子,分母不变;当整式是多项式时,同样要先分解因式.
分式乘以分式(整式)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
约分化为最简分式(整式)
除号变为乘号
分子、分母颠倒位置
整式
合作
分式的除法运算
转化为分式的乘法运算,然后按分式的乘法法则运算.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
约分化为最简分式(整式)
除号变为乘号
分子、分母颠倒位置
最简分式
分式的除法运算
若除式(或被除式)是整式,可把它看作分母是1的“分式”,然后按分式的除法法则运算.
合作
分母写成1
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例1 计算:
(1) ; (2) .
解:(1)
运算结果应化为最简分式.
(2)
抢答
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
解:(1)
例2 计算:
(1) ; (2) .
解:(2)
运算结果符号的确定方法与分数乘除符号的确定方法相同.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例3 如图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a–1) m的正方形,两块试验田的小麦都收获了500 kg.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
1 m
a m
(a–1) m
1 m
a m
(a–1) m
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例3 如图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a–1) m的正方形,两块试验田的小麦都收获了500 kg.
(1)哪种小麦的单位面积产量高?
解:(1)“丰收1号”小麦的试验田面积是(a2–1) m2,
单位面积产量是 kg/ m2.
“丰收2号”小麦的试验田面积是(a–1)2 m,
单位面积产量是 kg/ m2.
∵a>1,
∴ (a–1) 2 >0,a2–1>0.
由图
可得(a–1) 2 <a2–1.
所以“丰收2号”小麦的单位面积产量高.
因为a>1,
所以(a–1)2– (a2–1)
=(a2–2a+1) –(a2–1)
= –2(a–1)<0.
即(a–1) 2<a2–1.
作差法
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例3 如图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a–1) m的正方形,两块试验田的小麦都收获了500 kg.
(2)高的单位面积产量是低的单位面积产量的多少倍?
解:(2)
.
所以,“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
老师设计了接力游戏,甲、乙、丙、丁四位同学用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简过程如图所示,接力中,自己负责的一步出现错误的同学是 ( )
A. 甲 B. 乙 C. 丙 D. 丁
B
老师
甲
乙
丙
丁
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
(2) (3)
计算:
(1)
(2)
(3)
应用新知
课堂小结
布置作业
创设情境
练习3
探究新知
巩固新知
先化简,再求值.
其中
解:原式
当 时,原式=
随堂练习
应用新知
布置作业
创设情境
探究新知
巩固新知
练习4
课堂小结
课堂上,老师给大家出了这样一道题:当x=2021时,计算 的值.小邦同学把“ x=2021”错抄成“x=2201”,但他的计算结果也正确,你说这是怎么回事?
解:原式
∵结果与x的取值无关,
∴小邦同学的计算结果也正确.
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
分式的乘法法则
分式除以分式,把除式的分子、分母颠倒位置,与被除式相乘.
分式的除法法则
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式与分式相乘:
①若分子与分母是单项式,可先将分子、分母分别相乘,然后约去公因式,将结果化为最简分式或整式;
②若分子、分母是多项式,则先将分子、分母分解因式,再相乘,且其结果要化简为最简分式或整式.
分式和整式相乘:
只需要把整式(看作分母为1的式子)与分式的分子相乘,用其结果作为积的分子,分母不变;当整式是多项式时,同样要先分解因式.
分式的乘法
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
若除式(或被除式)是整式,可把它看作分母是1的“分式”,然后按分式的除法法则运算.
分式的除法
分式的乘除
布置作业
教科书第137页练习2、3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.2.1 分式的乘除
第1课时
学习目标
1.理解并掌握分式的乘除法法则;
2.运用法则进行运算,能解决一些与分式有关的实际问题;
3.经历探索分式的乘除运算法则的过程,培养学生类比的思想方法,提高分析问题,解决问题的能力;
4.通过联系实际探究分式乘除运算法则的过程,培养学生与他人的合作意识.
分式的乘除
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:一个水平放置的长方体容器,其容积为V,底面的长为a,宽为b,当容器内的水占容器的 时,水面的高度为多少?
长方体容器的高为 ,
水面的高度为 .
b
a
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题2:大拖拉机 m 天耕地 a hm2,小拖拉机 n 天耕地 b hm2,大拖拉机的工作效率是小拖拉机工作效率的多少倍?
大拖拉机的工作效率是 hm2/天;
小拖拉机的工作效率是 hm2/天;
大拖拉机的工作效率是小拖拉机工作效率的 倍.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
问题1:一个水平放置的长方体容器,其容积为V,底面的长为a,宽为b,当容器内的水占容器的 时,水面的高度为 .
问题2:大拖拉机 m 天耕地 a hm2,小拖拉机 n 天耕地 b hm2,大拖拉机的工作效率是小拖拉机工作效率的 倍.
从上面的问题可知,为讨论数量关系,有时需要进行分式的乘除运算.
那么分式的乘除运算该怎么计算呢?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
还记得分数的乘除法运算吗?
分数的乘法法则:
分数乘以分数,用分子相乘的积做分子,分母相乘的积做分母.
分数的除法法则:
分数除以分数,等于
被除数乘以除数的倒数.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
类比分数的乘除法法则,你能说出分式的乘除法法则吗?
分数的乘法法则:
分数乘以分数,用分子相乘的积做分子,分母相乘的积做分母.
分数的除法法则:
分数除以分数,等于
被除数乘以除数的倒数.
分式的除法法则:
分式除以分式,把除式的分子、分母颠倒位置,与被除式相乘.
分式的乘法法则:
分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
思考
分式的除法法则
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
分式的乘法法则
分式除以分式,把除式的分子、分母颠倒位置,与被除式相乘.
字母表示:
字母表示:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分母相乘
分子相乘
约分化为最简分式
最简
分式
分式乘以分式:
若分子与分母是单项式,可先将分子、分母分别相乘,然后约去公因式,将结果化为最简分式或整式.
合作
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
合作
分式和分式相乘:
若分子(分母)是多项式,则先将分子(分母)分解因式,再相乘,且其结果要化简为最简分式或整式.
因式分解
约分化为最简分式
最简
分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分母相乘
分子相乘
约分化为最简分式
整式
整式的分母看成1
合作
分式和整式相乘:
只需要把整式(看作分母为1的式子)与分式的分子相乘,用其结果作为积的分子,分母不变;当整式是多项式时,同样要先分解因式.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式与分式相乘:
①若分子与分母是单项式,可先将分子、分母分别相乘,然后约去公因式,将结果化为最简分式或整式;
②若分子、分母是多项式,则先将分子、分母分解因式,再相乘,且其结果要化简为最简分式或整式.
分式和整式相乘:
只需要把整式(看作分母为1的式子)与分式的分子相乘,用其结果作为积的分子,分母不变;当整式是多项式时,同样要先分解因式.
分式乘以分式(整式)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
约分化为最简分式(整式)
除号变为乘号
分子、分母颠倒位置
整式
合作
分式的除法运算
转化为分式的乘法运算,然后按分式的乘法法则运算.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
约分化为最简分式(整式)
除号变为乘号
分子、分母颠倒位置
最简分式
分式的除法运算
若除式(或被除式)是整式,可把它看作分母是1的“分式”,然后按分式的除法法则运算.
合作
分母写成1
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例1 计算:
(1) ; (2) .
解:(1)
运算结果应化为最简分式.
(2)
抢答
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
解:(1)
例2 计算:
(1) ; (2) .
解:(2)
运算结果符号的确定方法与分数乘除符号的确定方法相同.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例3 如图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a–1) m的正方形,两块试验田的小麦都收获了500 kg.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
1 m
a m
(a–1) m
1 m
a m
(a–1) m
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例3 如图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a–1) m的正方形,两块试验田的小麦都收获了500 kg.
(1)哪种小麦的单位面积产量高?
解:(1)“丰收1号”小麦的试验田面积是(a2–1) m2,
单位面积产量是 kg/ m2.
“丰收2号”小麦的试验田面积是(a–1)2 m,
单位面积产量是 kg/ m2.
∵a>1,
∴ (a–1) 2 >0,a2–1>0.
由图
可得(a–1) 2 <a2–1.
所以“丰收2号”小麦的单位面积产量高.
因为a>1,
所以(a–1)2– (a2–1)
=(a2–2a+1) –(a2–1)
= –2(a–1)<0.
即(a–1) 2<a2–1.
作差法
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例3 如图,“丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a–1) m的正方形,两块试验田的小麦都收获了500 kg.
(2)高的单位面积产量是低的单位面积产量的多少倍?
解:(2)
.
所以,“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
老师设计了接力游戏,甲、乙、丙、丁四位同学用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简过程如图所示,接力中,自己负责的一步出现错误的同学是 ( )
A. 甲 B. 乙 C. 丙 D. 丁
B
老师
甲
乙
丙
丁
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
(2) (3)
计算:
(1)
(2)
(3)
应用新知
课堂小结
布置作业
创设情境
练习3
探究新知
巩固新知
先化简,再求值.
其中
解:原式
当 时,原式=
随堂练习
应用新知
布置作业
创设情境
探究新知
巩固新知
练习4
课堂小结
课堂上,老师给大家出了这样一道题:当x=2021时,计算 的值.小邦同学把“ x=2021”错抄成“x=2201”,但他的计算结果也正确,你说这是怎么回事?
解:原式
∵结果与x的取值无关,
∴小邦同学的计算结果也正确.
随堂练习
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
分式的乘法法则
分式除以分式,把除式的分子、分母颠倒位置,与被除式相乘.
分式的除法法则
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式与分式相乘:
①若分子与分母是单项式,可先将分子、分母分别相乘,然后约去公因式,将结果化为最简分式或整式;
②若分子、分母是多项式,则先将分子、分母分解因式,再相乘,且其结果要化简为最简分式或整式.
分式和整式相乘:
只需要把整式(看作分母为1的式子)与分式的分子相乘,用其结果作为积的分子,分母不变;当整式是多项式时,同样要先分解因式.
分式的乘法
分式的乘除
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
若除式(或被除式)是整式,可把它看作分母是1的“分式”,然后按分式的除法法则运算.
分式的除法
分式的乘除
布置作业
教科书第137页练习2、3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
