人教版九年级上册21.1一元二次方程 课件 (共19张PPT)
文档属性
| 名称 | 人教版九年级上册21.1一元二次方程 课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
成功就在于“再坚持一下”的努力之中!
笑对初三
复习引入
认识“老朋友”
1、想一想我们都学过哪些方程?
2、下列方程分别是什么方程?
一元一次方程
二元一次方程
分式方程
?
21.1一元二次方程
1、了解一元二次方程的概念;正确掌握一元二次方程的一般形式并能判定一个数是否是一元二次方程的根;
2、通过学生自主学习、合作探究,培养学生分析问题、解决问题的能力以及对数学概念完整性和深刻性的理解;
3、培养学生学数学用数学的意识.
学习目标
理解一元二次方程的概念,认识一元二次方程的一般形式;
学习重点
学习难点
正确理解和掌握一般形式中的a≠0 ,“项”和“系数” .
自主学习
阅读课本P1-P3页,并回答下列问题:
1.什么叫一元二次方程?
2.下列方程哪些是一元二次方程?
是一元二次方程的有:
只含有一个未知数,且未知数的最高次数是2的整式方程,叫做一元二次方程。
合作探究(1)
判断一个方程是一元二次方程应满足什么条件?
①只含有一个未知数;
②方程两边都是整式;(即方程为整式方程)
③方程化简后,未知数的最高次数是2.
条件:
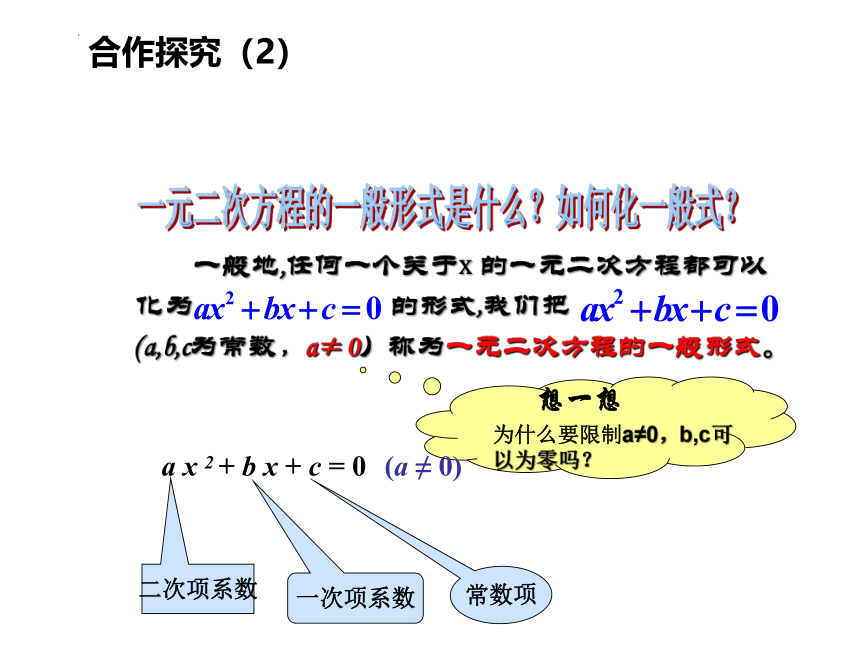
合作探究(2)
一元二次方程的一般形式是什么?如何化一般式?
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
为什么要限制a≠0,b,c可以为零吗?
想一想
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
合作探究
例题
将方程3x(x-1)=5(x+2)化为一元二次方程的
一般形式,并写出二次项系数、一次项系数及常数项。
解:去括号,得
3x2-3x=5x+10
移项,合并同类项得
3x2-8x-10=0
其中二次项系数为3,一次项系数为-8,常数项为-10
同步训练:见练习册P3页第18题
注:一般形式(1)右边为0;(2)按照所含未知数作降幂排列;(3)二次项系数一般为正。
合作探究(3)
什么叫一元二次方程的解(根)?你会判断一个数是否为方程的根吗?
使方程左右两边相等的未知数的值就是一元二次方程的解,一元二次方程的解也叫做一元二次方程的根。
同步训练:
下列哪些数是方程 的根?
x2+x-12=0
-4,-3,-2,-1,0,1,2,3,4
变式训练:练习册第7,12题
1.判断下列方程是否为一元二次方程:
2.当m为何值时,方程
是关于x的一元二次方程.
当堂检测
3. 将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:
⑴
⑵
⑶
(4)
原 方 程 一 般 形 式 二次项系数 一次项系数 常数项
5
-1
-4
5
-81
0
4
-25
8
3
1
-7
有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600平方厘米,那么铁皮各角应切去多大的正方形 若设切去的正方形的边长为xcm,列出关于x的方程,并将其化为一元二次方程的一般形式。
100㎝
50㎝
x
3600
即
能力提高
归纳小结
1.一元二次方程的概念;
2.一元二次方程的一般形式;
3.一元二次方程的根。
只含有一个未知数,并且未知数的最高次数
是2的整式方程叫做一元二次方程。
一般地,任何一个关于x 的一元二次方程
都可以化为 的形式,我们把
(a,b,c为常数,a≠0)称
为一元二次方程的一般形式。
拓展补充
典例分析
体验中考
1、已知是一元二次方程x +mx+2=0的一个解,则的值是( )
A.-3 B.3 C.0 D.0或3
(点拨:本题考查一元二次方程的解的意义.)
2、若n≠0是x +mx+2=0关于的方程的根,则的值为( )
A.1 B.2 C.-1 D.-2
(提示:本题有两个待定字母和,根据已知条件不能分别求出它们的值,故考虑运用整体思想,直接求出它们的和.)
成功就在于“再坚持一下”的努力之中!
笑对初三
复习引入
认识“老朋友”
1、想一想我们都学过哪些方程?
2、下列方程分别是什么方程?
一元一次方程
二元一次方程
分式方程
?
21.1一元二次方程
1、了解一元二次方程的概念;正确掌握一元二次方程的一般形式并能判定一个数是否是一元二次方程的根;
2、通过学生自主学习、合作探究,培养学生分析问题、解决问题的能力以及对数学概念完整性和深刻性的理解;
3、培养学生学数学用数学的意识.
学习目标
理解一元二次方程的概念,认识一元二次方程的一般形式;
学习重点
学习难点
正确理解和掌握一般形式中的a≠0 ,“项”和“系数” .
自主学习
阅读课本P1-P3页,并回答下列问题:
1.什么叫一元二次方程?
2.下列方程哪些是一元二次方程?
是一元二次方程的有:
只含有一个未知数,且未知数的最高次数是2的整式方程,叫做一元二次方程。
合作探究(1)
判断一个方程是一元二次方程应满足什么条件?
①只含有一个未知数;
②方程两边都是整式;(即方程为整式方程)
③方程化简后,未知数的最高次数是2.
条件:
合作探究(2)
一元二次方程的一般形式是什么?如何化一般式?
一般地,任何一个关于x 的一元二次方程都可以
化为 的形式,我们把
(a,b,c为常数,a≠0)称为一元二次方程的一般形式。
为什么要限制a≠0,b,c可以为零吗?
想一想
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
合作探究
例题
将方程3x(x-1)=5(x+2)化为一元二次方程的
一般形式,并写出二次项系数、一次项系数及常数项。
解:去括号,得
3x2-3x=5x+10
移项,合并同类项得
3x2-8x-10=0
其中二次项系数为3,一次项系数为-8,常数项为-10
同步训练:见练习册P3页第18题
注:一般形式(1)右边为0;(2)按照所含未知数作降幂排列;(3)二次项系数一般为正。
合作探究(3)
什么叫一元二次方程的解(根)?你会判断一个数是否为方程的根吗?
使方程左右两边相等的未知数的值就是一元二次方程的解,一元二次方程的解也叫做一元二次方程的根。
同步训练:
下列哪些数是方程 的根?
x2+x-12=0
-4,-3,-2,-1,0,1,2,3,4
变式训练:练习册第7,12题
1.判断下列方程是否为一元二次方程:
2.当m为何值时,方程
是关于x的一元二次方程.
当堂检测
3. 将下列方程化为一般形式,并分别指出它们的二次项、一次项和常数项及它们的系数:
⑴
⑵
⑶
(4)
原 方 程 一 般 形 式 二次项系数 一次项系数 常数项
5
-1
-4
5
-81
0
4
-25
8
3
1
-7
有一块矩形铁皮,长100㎝,宽50㎝,在它的四角各切去一个正方形,然后将四周突出部分折起,就能制作一个无盖方盒,如果要制作的方盒的底面积为3600平方厘米,那么铁皮各角应切去多大的正方形 若设切去的正方形的边长为xcm,列出关于x的方程,并将其化为一元二次方程的一般形式。
100㎝
50㎝
x
3600
即
能力提高
归纳小结
1.一元二次方程的概念;
2.一元二次方程的一般形式;
3.一元二次方程的根。
只含有一个未知数,并且未知数的最高次数
是2的整式方程叫做一元二次方程。
一般地,任何一个关于x 的一元二次方程
都可以化为 的形式,我们把
(a,b,c为常数,a≠0)称
为一元二次方程的一般形式。
拓展补充
典例分析
体验中考
1、已知是一元二次方程x +mx+2=0的一个解,则的值是( )
A.-3 B.3 C.0 D.0或3
(点拨:本题考查一元二次方程的解的意义.)
2、若n≠0是x +mx+2=0关于的方程的根,则的值为( )
A.1 B.2 C.-1 D.-2
(提示:本题有两个待定字母和,根据已知条件不能分别求出它们的值,故考虑运用整体思想,直接求出它们的和.)
同课章节目录
