2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册1.4.2用空间向量研究距离、夹角问题(2)课件-(共25张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册1.4.2用空间向量研究距离、夹角问题(2)课件-(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 37.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-21 23:28:18 | ||
图片预览




文档简介
(共25张PPT)
1.4.2用空间向量研究
距离、夹角问题2
求异面直线所成角
设异面直线1,,所成角为0,显然e(0,1,设其方向向量分别为4,立,而<4,v>∈(0,)
h1,
0=<4,V>
0=π-<4,v>
cos 0=lcos
训
如图,在棱长为1的正四面体(四个面都是正三角形)
例7
ABCD中,M,N分别BC,AD的中点,
求直线AM和CN夹角的余弦值.
解:以{CA,cB,CD作为基底,则
化为向量问题
d-ciM-a-饿不A+Cm,
M-2@+而(-2@而.a1⑦a
=
2
叉Md-e-
进行向量运算
1
CN-MA
cos CN,MA>=
2
2
CNMA
3
V3
3
2
2
二直线AM和CN夹角的余弦值为
回到图形问题
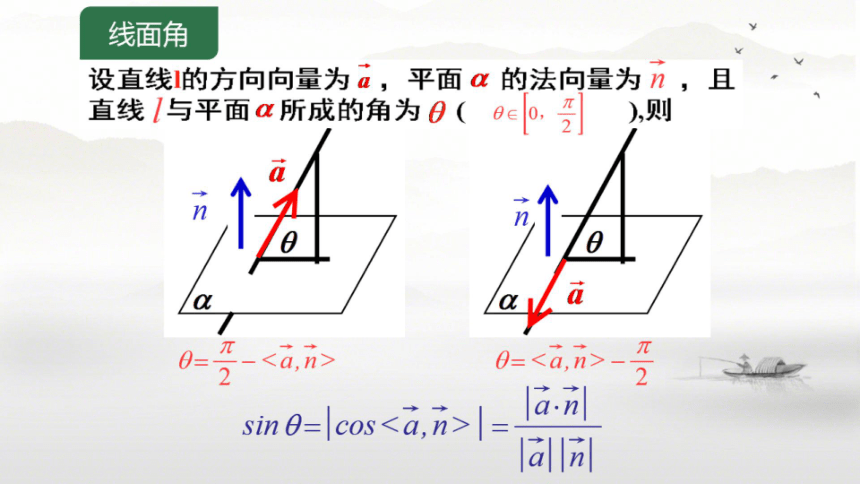
线面角
设直线的方向向量为a,平面a的法向量为n,且
直线1与平面a所成的角为0(0c0,引
),则
7
L
0=
2
0=-
π
2
sin 0=cos
la.n
1al
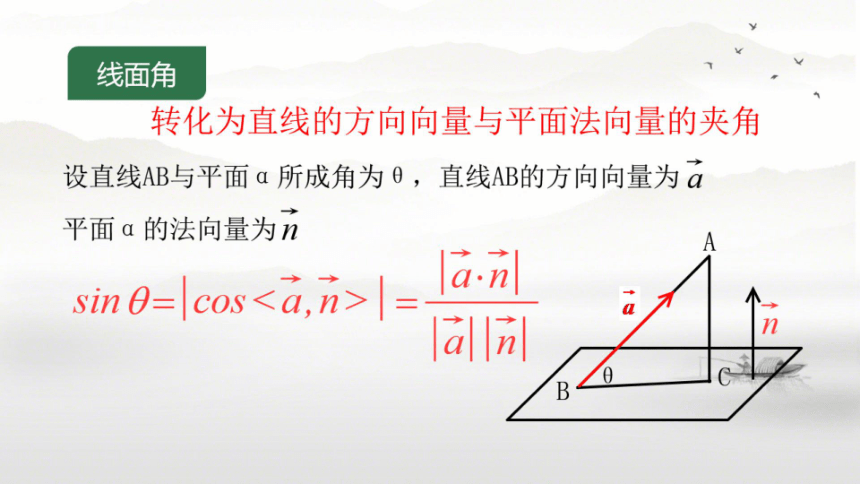
线面角
转化为直线的方向向量与平面法向量的夹角
设直线AB与平面a所成角为0,直线AB的方向向量为a
平面a的法向量为n
sin 0=cos=
la.n
lal
B
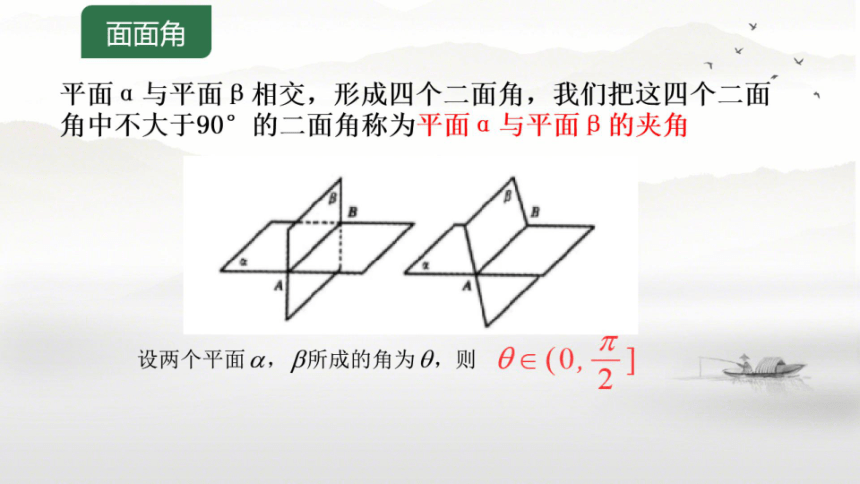
面面角
平面α与平面B相交,形成四个二面角,我们把这四个二面
角中不大于90°的二面角称为平面α与平面B的夹角
设两个平面a,所成的角为0.则6c(0,]
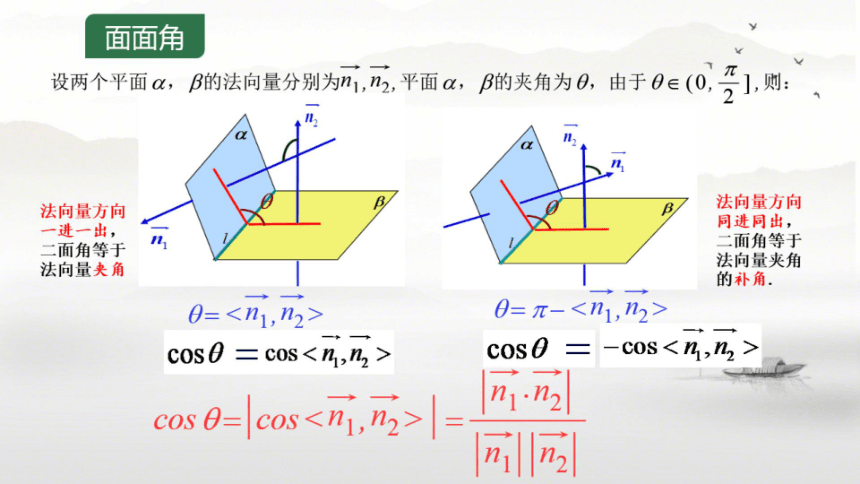
面面角
设两个平面a,B的法向量分别为n1,n,平面x,的夹角为0,由于0∈(0,7],则:
7
法向量方向
法向量方向
一进一出,
同进同出,
二面角等于
二面角等于
法向量夹角
法向量夹角
的补角.
0=
0=π-
cos cos
c0S0=
-C0S
cos 0=cos=
n.n2
2
面面角
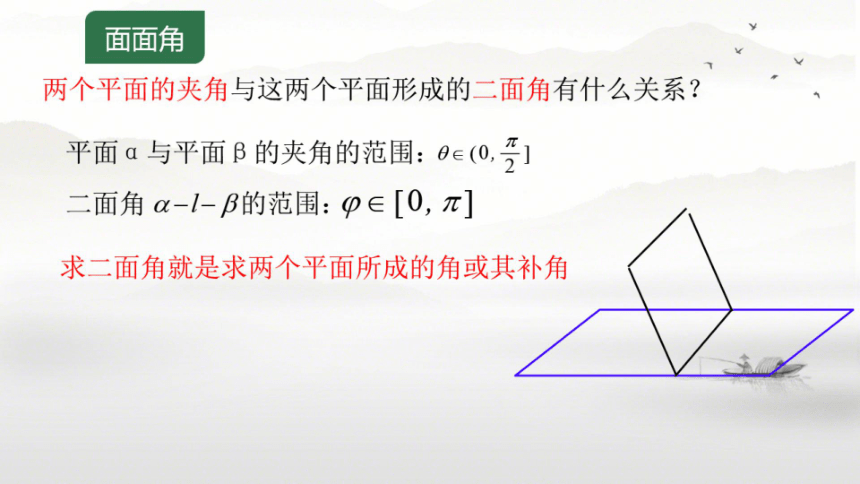
两个平面的夹角与这两个平面形成的二面角有什么关系?
平面a与平面B的夹角的范围:6c(0,]
二面角a-l-B的范围:p∈[0,π]
求二面角就是求两个平面所成的角或其补角
设直线1,m的方向向量分别为a,方,平面au,B的法向量分别为n1,n2,-则
异面直线所成角:cos0-|cs=a-列
a
0e0,1
线面角:m0=cos=a-列
a
o引
二面角:cos0=cos=
n.n
0∈[0,π]
求二面角就是求两个平面所成的角或其补角
1.4.2用空间向量研究
距离、夹角问题2
求异面直线所成角
设异面直线1,,所成角为0,显然e(0,1,设其方向向量分别为4,立,而<4,v>∈(0,)
h1,
0=<4,V>
0=π-<4,v>
cos 0=lcos
训
如图,在棱长为1的正四面体(四个面都是正三角形)
例7
ABCD中,M,N分别BC,AD的中点,
求直线AM和CN夹角的余弦值.
解:以{CA,cB,CD作为基底,则
化为向量问题
d-ciM-a-饿不A+Cm,
M-2@+而(-2@而.a1⑦a
=
2
叉Md-e-
进行向量运算
1
CN-MA
cos CN,MA>=
2
2
CNMA
3
V3
3
2
2
二直线AM和CN夹角的余弦值为
回到图形问题
线面角
设直线的方向向量为a,平面a的法向量为n,且
直线1与平面a所成的角为0(0c0,引
),则
7
L
0=
2
0=
π
2
sin 0=cos
la.n
1al
线面角
转化为直线的方向向量与平面法向量的夹角
设直线AB与平面a所成角为0,直线AB的方向向量为a
平面a的法向量为n
sin 0=cos
la.n
lal
B
面面角
平面α与平面B相交,形成四个二面角,我们把这四个二面
角中不大于90°的二面角称为平面α与平面B的夹角
设两个平面a,所成的角为0.则6c(0,]
面面角
设两个平面a,B的法向量分别为n1,n,平面x,的夹角为0,由于0∈(0,7],则:
7
法向量方向
法向量方向
一进一出,
同进同出,
二面角等于
二面角等于
法向量夹角
法向量夹角
的补角.
0=
0=π-
cos cos
c0S0=
-C0S
cos 0=cos
n.n2
2
面面角
两个平面的夹角与这两个平面形成的二面角有什么关系?
平面a与平面B的夹角的范围:6c(0,]
二面角a-l-B的范围:p∈[0,π]
求二面角就是求两个平面所成的角或其补角
设直线1,m的方向向量分别为a,方,平面au,B的法向量分别为n1,n2,-则
异面直线所成角:cos0-|cs
a
0e0,1
线面角:m0=cos
a
o引
二面角:cos0=cos
n.n
0∈[0,π]
求二面角就是求两个平面所成的角或其补角
