2022—2023学年人教版数学八年级上册11.2.1 三角形的内角 同步练习 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.1 三角形的内角 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 300.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:08:59 | ||
图片预览


文档简介
11.2.1 三角形的内角
一、选择题(共4小题)
1. 在 △ABC 中,∠C=90 ,∠B=25 ,则 ∠A 的度数为
A. 25 B. 75 C. 55 D. 65
2. 如图,在 △ABC 中,∠C=90 ,则 ∠B 的度数为
A. 15 B. 30 C. 50 D. 60
3. 下列条件中能判断 △ABC 为直角三角形的是
A. ∠A+∠B=∠C B. ∠A=∠B=∠C
C. ∠A ∠B=90 D. ∠A=∠B=3∠C
4. 如图,∠BAC=90 ,AD⊥BC,则图中互余的角有
A. 2 对 B. 3 对 C. 4 对 D. 5 对
二、填空题(共5小题)
5. 直角三角形的性质:直角三角形的两个锐角互余.
几何语言:在 Rt△ABC 中,∠C=90 ,
∴∠A+∠B= .
如:在直角三角形中,其中一个锐角是 35 ,则另一个锐角是 .
6. 直角三角形的判定:有两个角互余的三角形是直角三角形.
几何语言:在 △ABC 中,∠A+∠B=90 ,
∴∠C= ,即 △ABC 是 三角形.
如:已知 △ABC 的两个角分别为 20 和 70 ,则 △ABC 一定是 三角形.
7. 在直角三角形中,一个锐角比另一个锐角的 3 倍还多 14 ,则较大锐角的度数为 .
8. 如图,CE⊥AD,AB⊥CD,∠C=50 ,则 ∠A 的度数为 .
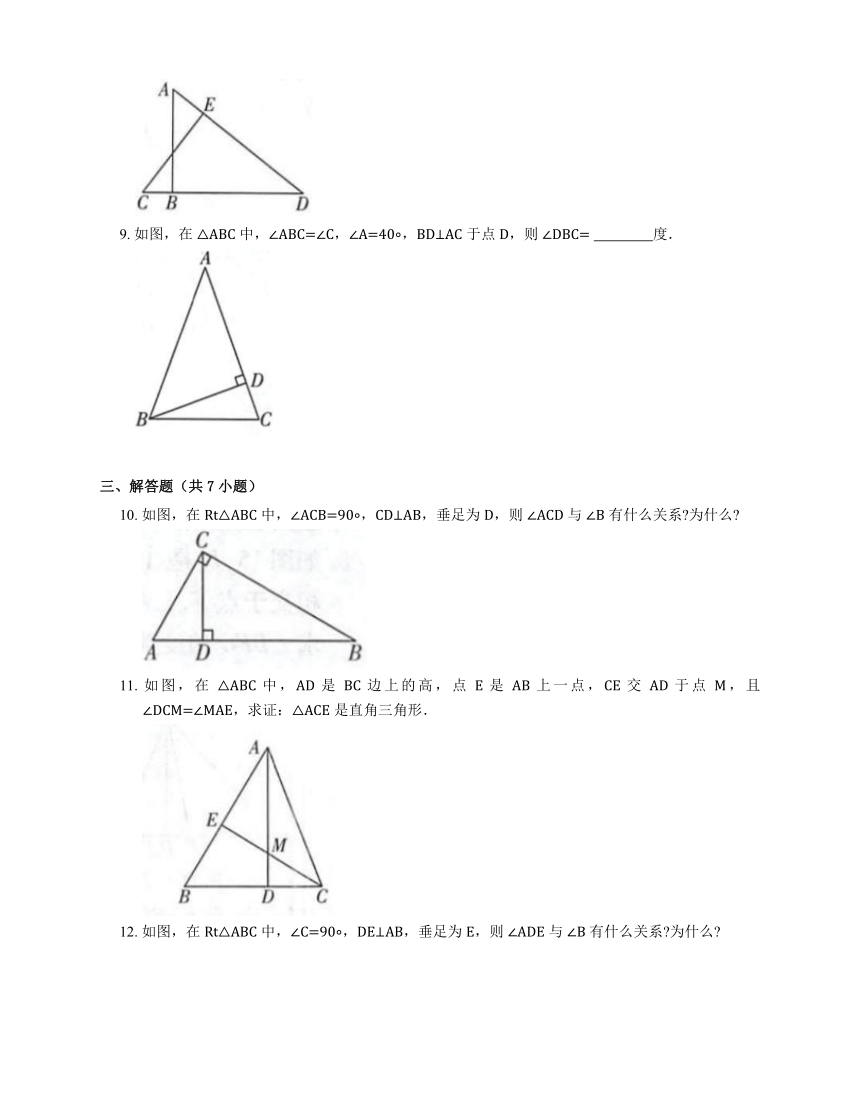
9. 如图,在 △ABC 中,∠ABC=∠C,∠A=40 ,BD⊥AC 于点 D,则 ∠DBC= 度.
三、解答题(共7小题)
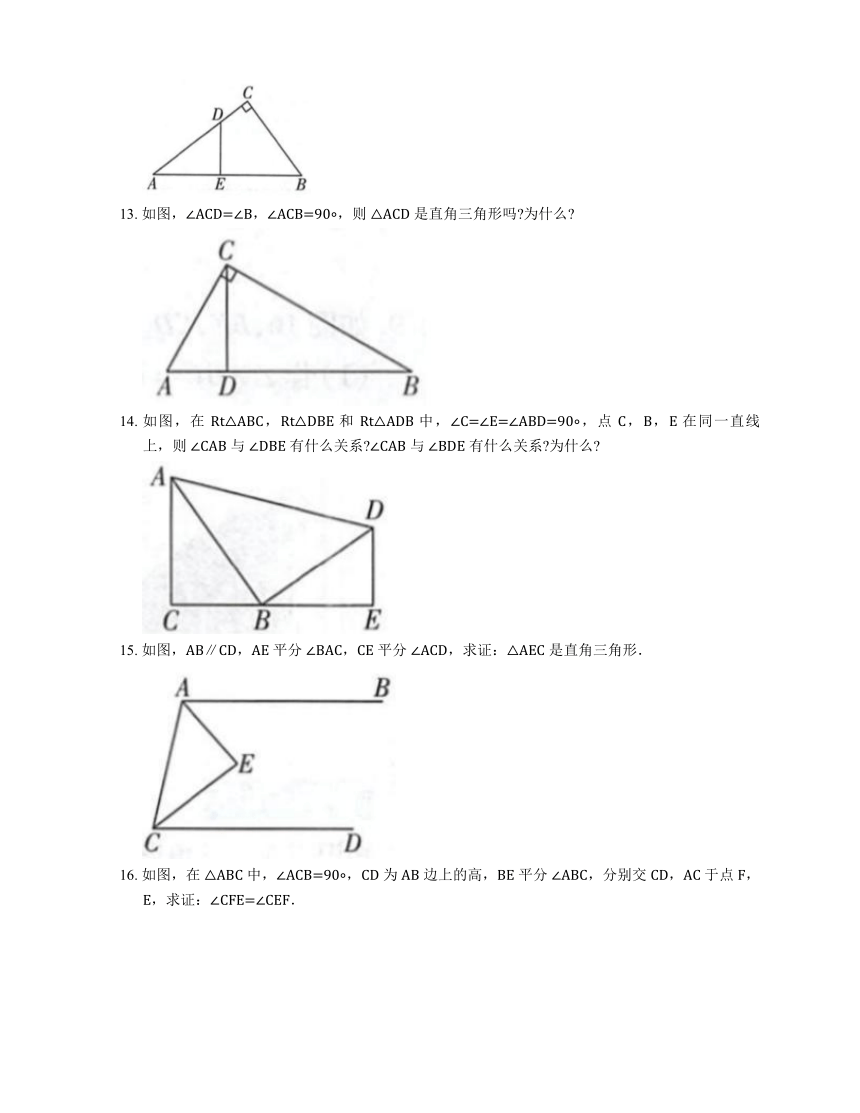
10. 如图,在 Rt△ABC 中,∠ACB=90 ,CD⊥AB,垂足为 D,则 ∠ACD 与 ∠B 有什么关系 为什么
11. 如图,在 △ABC 中,AD 是 BC 边上的高,点 E 是 AB 上一点,CE 交 AD 于点 M,且 ∠DCM=∠MAE,求证:△ACE 是直角三角形.
12. 如图,在 Rt△ABC 中,∠C=90 ,DE⊥AB,垂足为 E,则 ∠ADE 与 ∠B 有什么关系 为什么
13. 如图,∠ACD=∠B,∠ACB=90 ,则 △ACD 是直角三角形吗 为什么
14. 如图,在 Rt△ABC,Rt△DBE 和 Rt△ADB 中,∠C=∠E=∠ABD=90 ,点 C,B,E 在同一直线上,则 ∠CAB 与 ∠DBE 有什么关系 ∠CAB 与 ∠BDE 有什么关系 为什么
15. 如图,AB∥CD,AE 平分 ∠BAC,CE 平分 ∠ACD,求证:△AEC 是直角三角形.
16. 如图,在 △ABC 中,∠ACB=90 ,CD 为 AB 边上的高,BE 平分 ∠ABC,分别交 CD,AC 于点 F,E,求证:∠CFE=∠CEF.
答案
1. D
2. D
3. A
4. C
5. 90 ,55
6. 90 ,直角,直角
7. 71
8. 50
9. 20
10. ∠ACD=∠B.
理由:∵∠ACB=90 ,CD⊥AB,
∴∠ACD+∠BCD=∠ACB=90 ,∠B+∠BCD=180 90 =90 .
∴∠ACD=∠B.
11. ∵AD 是 BC 边上的高,
∴∠DMC+∠DCM=90 ,
∵∠DMC=∠AME,∠DCM=∠MAE,
∴∠AME+∠MAE=90 ,
∴△ACE 是直角三角形.
12. ∠ADE=∠B.
理由:
∵∠ACB=90 ,DE⊥AB,
∴∠A+∠B=90 =∠A+∠ADE.
∴∠ADE=∠B.
13. △ACD 是直角三角形.
理由:
∵∠ACB=90 ,
∴∠A+∠B=90 .
∵∠ACD=∠B,
∴∠A+∠ACD=90 .
∴△ACD 是直角三角形.
14. ∠CAB=∠DBE,∠CAB+∠BDE=90 .
理由:在 Rt△ABC 中,∠C=90 ,
∴∠ABC+∠CAB=90 .
∵∠ABD=90 ,
∴∠ABC+∠DBE=180 ∠ABD=90 .
∴∠CAB=∠DBE.
在 Rt△DBE 中,∠E=90 ,
∴∠DBE+∠BDE=90 .
∴∠CAB+∠BDE=90 .
15. ∵AB∥CD,
∴∠BAC+∠ACD=180 ,
∵AE 平分 ∠BAC,CE 平分 ∠ACD,
∴∠EAC=12∠BAC,∠ACE=12∠ACD.
∴∠EAC+∠ACE=12∠BAC+∠ACD=90 .
∴△AEC 是直角三角形.
16. 如图.
∵∠ACB=90 ,
∴∠1+∠3=90 .
∵CD 为 AB 边上的高,
∴∠2+∠4=90 .
∵BE 平分 ∠ABC,
∴∠1=∠2.
∴∠3=∠4.
又 ∠4=∠5,
∴∠3=∠5,即 ∠CFE=∠CEF.
一、选择题(共4小题)
1. 在 △ABC 中,∠C=90 ,∠B=25 ,则 ∠A 的度数为
A. 25 B. 75 C. 55 D. 65
2. 如图,在 △ABC 中,∠C=90 ,则 ∠B 的度数为
A. 15 B. 30 C. 50 D. 60
3. 下列条件中能判断 △ABC 为直角三角形的是
A. ∠A+∠B=∠C B. ∠A=∠B=∠C
C. ∠A ∠B=90 D. ∠A=∠B=3∠C
4. 如图,∠BAC=90 ,AD⊥BC,则图中互余的角有
A. 2 对 B. 3 对 C. 4 对 D. 5 对
二、填空题(共5小题)
5. 直角三角形的性质:直角三角形的两个锐角互余.
几何语言:在 Rt△ABC 中,∠C=90 ,
∴∠A+∠B= .
如:在直角三角形中,其中一个锐角是 35 ,则另一个锐角是 .
6. 直角三角形的判定:有两个角互余的三角形是直角三角形.
几何语言:在 △ABC 中,∠A+∠B=90 ,
∴∠C= ,即 △ABC 是 三角形.
如:已知 △ABC 的两个角分别为 20 和 70 ,则 △ABC 一定是 三角形.
7. 在直角三角形中,一个锐角比另一个锐角的 3 倍还多 14 ,则较大锐角的度数为 .
8. 如图,CE⊥AD,AB⊥CD,∠C=50 ,则 ∠A 的度数为 .
9. 如图,在 △ABC 中,∠ABC=∠C,∠A=40 ,BD⊥AC 于点 D,则 ∠DBC= 度.
三、解答题(共7小题)
10. 如图,在 Rt△ABC 中,∠ACB=90 ,CD⊥AB,垂足为 D,则 ∠ACD 与 ∠B 有什么关系 为什么
11. 如图,在 △ABC 中,AD 是 BC 边上的高,点 E 是 AB 上一点,CE 交 AD 于点 M,且 ∠DCM=∠MAE,求证:△ACE 是直角三角形.
12. 如图,在 Rt△ABC 中,∠C=90 ,DE⊥AB,垂足为 E,则 ∠ADE 与 ∠B 有什么关系 为什么
13. 如图,∠ACD=∠B,∠ACB=90 ,则 △ACD 是直角三角形吗 为什么
14. 如图,在 Rt△ABC,Rt△DBE 和 Rt△ADB 中,∠C=∠E=∠ABD=90 ,点 C,B,E 在同一直线上,则 ∠CAB 与 ∠DBE 有什么关系 ∠CAB 与 ∠BDE 有什么关系 为什么
15. 如图,AB∥CD,AE 平分 ∠BAC,CE 平分 ∠ACD,求证:△AEC 是直角三角形.
16. 如图,在 △ABC 中,∠ACB=90 ,CD 为 AB 边上的高,BE 平分 ∠ABC,分别交 CD,AC 于点 F,E,求证:∠CFE=∠CEF.
答案
1. D
2. D
3. A
4. C
5. 90 ,55
6. 90 ,直角,直角
7. 71
8. 50
9. 20
10. ∠ACD=∠B.
理由:∵∠ACB=90 ,CD⊥AB,
∴∠ACD+∠BCD=∠ACB=90 ,∠B+∠BCD=180 90 =90 .
∴∠ACD=∠B.
11. ∵AD 是 BC 边上的高,
∴∠DMC+∠DCM=90 ,
∵∠DMC=∠AME,∠DCM=∠MAE,
∴∠AME+∠MAE=90 ,
∴△ACE 是直角三角形.
12. ∠ADE=∠B.
理由:
∵∠ACB=90 ,DE⊥AB,
∴∠A+∠B=90 =∠A+∠ADE.
∴∠ADE=∠B.
13. △ACD 是直角三角形.
理由:
∵∠ACB=90 ,
∴∠A+∠B=90 .
∵∠ACD=∠B,
∴∠A+∠ACD=90 .
∴△ACD 是直角三角形.
14. ∠CAB=∠DBE,∠CAB+∠BDE=90 .
理由:在 Rt△ABC 中,∠C=90 ,
∴∠ABC+∠CAB=90 .
∵∠ABD=90 ,
∴∠ABC+∠DBE=180 ∠ABD=90 .
∴∠CAB=∠DBE.
在 Rt△DBE 中,∠E=90 ,
∴∠DBE+∠BDE=90 .
∴∠CAB+∠BDE=90 .
15. ∵AB∥CD,
∴∠BAC+∠ACD=180 ,
∵AE 平分 ∠BAC,CE 平分 ∠ACD,
∴∠EAC=12∠BAC,∠ACE=12∠ACD.
∴∠EAC+∠ACE=12∠BAC+∠ACD=90 .
∴△AEC 是直角三角形.
16. 如图.
∵∠ACB=90 ,
∴∠1+∠3=90 .
∵CD 为 AB 边上的高,
∴∠2+∠4=90 .
∵BE 平分 ∠ABC,
∴∠1=∠2.
∴∠3=∠4.
又 ∠4=∠5,
∴∠3=∠5,即 ∠CFE=∠CEF.
