2022—2023学年人教版数学八年级上册11.2.2 三角形的外角 同步练习 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.2.2 三角形的外角 同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 963.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:12:27 | ||
图片预览




文档简介
11.2.2 三角形的外角
一、选择题(共3小题)
1. 如图,点 B,C,D 在同一直线上,则 ∠1,∠2,∠3 的大小关系是
A. ∠1<∠2<∠3 B. ∠1<∠3<∠2 C. ∠2<∠3<∠1 D. ∠3<∠2<∠1
2. 三角形的一个外角是锐角,则这个三角形是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
3. 若一个三角形三个内角之比为 2:3:4,则相应的三个外角之比为
A. 2:3:4 B. 4:3:2 C. 5:4:3 D. 7:6:5
二、填空题(共9小题)
4. 求图中各未知角的度数:∠1= ;∠2= ;∠3= ;∠4= .
5. 如图,一副三角板叠放在一起,则图中 ∠α 的度数是 .
6. 如图所示,∠ABD 的度数是 .
7. 在 △ABC 中,已知 ∠A+∠B ∠C=20 ,则 ∠C= (填度数).
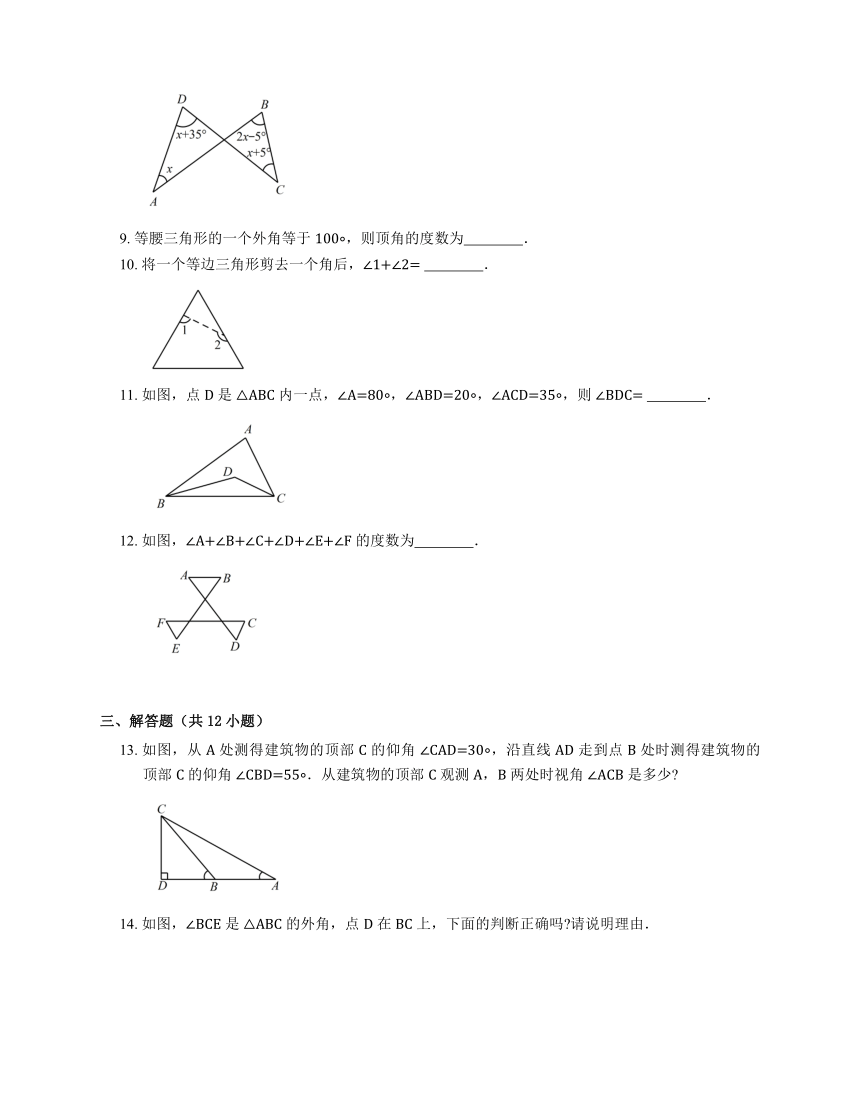
8. 如图,∠DAB 的度数是 .
9. 等腰三角形的一个外角等于 100 ,则顶角的度数为 .
10. 将一个等边三角形剪去一个角后,∠1+∠2= .
11. 如图,点 D 是 △ABC 内一点,∠A=80 ,∠ABD=20 ,∠ACD=35 ,则 ∠BDC= .
12. 如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为 .
三、解答题(共12小题)
13. 如图,从 A 处测得建筑物的顶部 C 的仰角 ∠CAD=30 ,沿直线 AD 走到点 B 处时测得建筑物的顶部 C 的仰角 ∠CBD=55 .从建筑物的顶部 C 观测 A,B 两处时视角 ∠ACB 是多少
14. 如图,∠BCE 是 △ABC 的外角,点 D 在 BC 上,下面的判断正确吗 请说明理由.
(1)∠1=∠A+∠B+∠E;
(2)∠1>∠A.
15. (1)如图,小明沿画在操场上的 △ABC 的边逆时针走一圈回到原地,小明一共旋转的度数是 ;
(2)请在图中标出小明在每个顶点处转过的角度;
(3)在图中,小明所转过的角度的总和可以用式子表示为 .
你能说明式子成立的理由吗 答: .
16. 如图,DE 分别与 △ABC 的边 AB,BC 相交于点 D,E,与 AC 的延长线相交于点 F,∠A=25 ,∠B=30 ,∠BED=100 ,求 ∠F 的度数.
17. 如图,CD 是 △ABC 的高,AE 是 △ABC 的角平分线,∠BAC=50 ,求 ∠AFC 的度数.
18. 如图,△ABC 中,BD 是 △ABC 的角平分线,DE∥BC 交 AB 于 E,∠A=80 ,∠BDC=110 ,求 △BDE 各内角的度数.
19. 如图①,∠BAD 与 ∠ACF 是 △ABC 的外角,点 E 在 AB 上,那么 ∠ACF 与 ∠D 的大小关系如何 小明直接用图 ①给出理由,小华用图②给出理由,你知道他们各自的说理方法吗
20. 如图,一个零件按规定 ∠A=90 ,∠B=32 ,∠C=23 .检验工人量得 ∠BDC=143 ,就断定这个零件不合格,请你运用三角形的有关知识说明不合格的理由.如果测得 ∠BDC=145 ,能说明这个零件一定合格吗
21. 如图,在 △ABC 中,∠ABC 与 ∠ACB 的平分线相交于点 I,根据下列条件,求 ∠BIC 的度数.
(1)若 ∠ABC=60 ,∠ACB=70 ,则 ∠BIC= ;
(2)若 ∠ABC+∠ACB=130 ,则 ∠BIC= ;
(3)若 ∠A=50 ,则 ∠BIC= ;
(4)从上述计算中,我们发现 ∠A 与 ∠BIC 之间有怎样的数量关系 请说明理由.
22. 如图,已知 △ABC 中,∠ABC 的平分线与外角 ∠ACD 的平分线相交于点 I,∠A 与 ∠BIC 之间有怎样的数量关系 请说明理由.
23. 如图,在 △ABC 中,∠BAC=∠BCA,CD 平分 ∠ACB,CE⊥AB 交 AB 的延长线于点 E,若 ∠DCE=54 ,求 ∠A 的度数.
24. 如图,在 △ABC 中,分别与 ∠ABC,∠ACB 相邻的两外角的角平分线相交于点 I,∠A 与 ∠BIC 之间有怎样的数量关系 请说明理由.
答案
1. C
2. C
3. D
4. 80 ,100 ,60 ,105
5. 105
6. 120
7. 80
8. 35
9. 80 或 20
10. 240
11. 135
12. 360
13. 由题意得,∠CBD 是 △ABC 的一个外角,
∴ ∠CBD=∠ACB+∠CAD.
∴ ∠ACB=∠CBD ∠CAD=55 30 =25 .
14. (1) 正确,理由如下:
∵ ∠BCE 是 △ABC 的外角,
∴ ∠BCE=∠A+∠B,
又 ∵ ∠1 是 △CDE 的外角,
∴ ∠1=∠BCE+∠E,
∴ ∠1=∠BCE+∠E=∠A+∠B+∠E
(2) 正确,理由如下:
由 1 得,∠1=∠A+∠B+∠E,
∵ ∠B>0 ,∠E>0 ,
∴ ∠1>∠A .
15. (1) 360
(2) 如图所示.
(3) ∠1+∠2+∠3=360 ;三角形的外角和等于 360
16. ∠ADF=∠B+∠BED=30 +100 =130 ,
在 △ADF 中,∠F=180 ∠A ∠ADF=180 25 130 =25 .
17. ∵ AE 是 △ABC 的角平分线,
∴ ∠BAE=12∠BAC=12×50 =25 .
∵ CD 是 △ABC 的高,
∴ ∠ADC=90 .
∴ ∠AFC=∠DAF+∠ADF=25 +90 =115 .
18. 在 △ABD 中,
∠ABD=∠BDC ∠A=110 80 =30 ,
因为 BD 是 △ABC 的角平分线,
所以 ∠CBD=∠ABD=30 .
因为 DE∥BC,
所以 ∠EDB=∠CBD=30 .
在 △BDE 中,∠BED=180 ∠ABD ∠EDB=180 30 30 =120 .
19. 小明的理由:在 △ABC 中,外角 ∠ACF>∠BAC.
在 △ADE 中,外角 ∠BAC>∠D.
所以 ∠ACF>∠D.
小华的理由:在 △DE C 中,外角 ∠DCF>∠D.
20. 如图,连接 A D 并延长至点 E,
∠BDC=∠BDE+∠EDC=∠B+∠BAE+∠C+∠EAC=∠BAC+∠B+∠C=145 .
(1)检验工人量得 ∠BDC=143 ≠145 ,
所以零件不合格;
(2)如果测得 ∠BDC=145 ,这个零件不一定合格 .当 ∠A=90 ,∠B=35 ,∠C=20 时,∠BDC=145 ,但此零件不合格.
21. (1) 115
(2) 115
(3) 115
(4) ∠BIC=90 +12∠A.
设 ∠ABI=∠IBC=x,∠ACI=∠ICB=y,
在 △ABC 中,2x+2y=180 ∠A,
所以 x+y=90 12∠A.
在 △IBC 中,∠BIC=180 x+y=180 90 12∠A=90 +12∠A.
22. ∠BIC=12∠A,理由如下:
设 ∠ABI=∠IBC=x,∠ACI=∠ICD=y,
在 △ABC 中,2y 2x=∠A,
所以 y x=12∠A,
在 △IBC 中,∠BIC=y x=12∠A.
23. 设 ∠ACD=x .
∵CD 平分 ∠ACB,
∴∠BCD=∠ACD=x .
又 ∠BAC=∠BCA,
∴∠BAC=∠BCA=2x .
∴∠CBE=4x .
∵∠CBE+∠BCE=90 ,∠DCE=54 ,
∴4x+54 x=90 .
解得 x=12 .
∴∠A=2x=24 .
24. ∠BIC=90 12∠A.
设 ∠CBI=∠IBD=x,∠BCI=∠ICE=y,
∵△ABC 的外角和等于 360 ,
∴2x+2y+180 ∠A=360 ,
∴x+y=90 +12∠A.
在 △IBC 中,
∠BIC=180 x+y=180 90 +12∠A=90 12∠A.
一、选择题(共3小题)
1. 如图,点 B,C,D 在同一直线上,则 ∠1,∠2,∠3 的大小关系是
A. ∠1<∠2<∠3 B. ∠1<∠3<∠2 C. ∠2<∠3<∠1 D. ∠3<∠2<∠1
2. 三角形的一个外角是锐角,则这个三角形是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不能确定
3. 若一个三角形三个内角之比为 2:3:4,则相应的三个外角之比为
A. 2:3:4 B. 4:3:2 C. 5:4:3 D. 7:6:5
二、填空题(共9小题)
4. 求图中各未知角的度数:∠1= ;∠2= ;∠3= ;∠4= .
5. 如图,一副三角板叠放在一起,则图中 ∠α 的度数是 .
6. 如图所示,∠ABD 的度数是 .
7. 在 △ABC 中,已知 ∠A+∠B ∠C=20 ,则 ∠C= (填度数).
8. 如图,∠DAB 的度数是 .
9. 等腰三角形的一个外角等于 100 ,则顶角的度数为 .
10. 将一个等边三角形剪去一个角后,∠1+∠2= .
11. 如图,点 D 是 △ABC 内一点,∠A=80 ,∠ABD=20 ,∠ACD=35 ,则 ∠BDC= .
12. 如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为 .
三、解答题(共12小题)
13. 如图,从 A 处测得建筑物的顶部 C 的仰角 ∠CAD=30 ,沿直线 AD 走到点 B 处时测得建筑物的顶部 C 的仰角 ∠CBD=55 .从建筑物的顶部 C 观测 A,B 两处时视角 ∠ACB 是多少
14. 如图,∠BCE 是 △ABC 的外角,点 D 在 BC 上,下面的判断正确吗 请说明理由.
(1)∠1=∠A+∠B+∠E;
(2)∠1>∠A.
15. (1)如图,小明沿画在操场上的 △ABC 的边逆时针走一圈回到原地,小明一共旋转的度数是 ;
(2)请在图中标出小明在每个顶点处转过的角度;
(3)在图中,小明所转过的角度的总和可以用式子表示为 .
你能说明式子成立的理由吗 答: .
16. 如图,DE 分别与 △ABC 的边 AB,BC 相交于点 D,E,与 AC 的延长线相交于点 F,∠A=25 ,∠B=30 ,∠BED=100 ,求 ∠F 的度数.
17. 如图,CD 是 △ABC 的高,AE 是 △ABC 的角平分线,∠BAC=50 ,求 ∠AFC 的度数.
18. 如图,△ABC 中,BD 是 △ABC 的角平分线,DE∥BC 交 AB 于 E,∠A=80 ,∠BDC=110 ,求 △BDE 各内角的度数.
19. 如图①,∠BAD 与 ∠ACF 是 △ABC 的外角,点 E 在 AB 上,那么 ∠ACF 与 ∠D 的大小关系如何 小明直接用图 ①给出理由,小华用图②给出理由,你知道他们各自的说理方法吗
20. 如图,一个零件按规定 ∠A=90 ,∠B=32 ,∠C=23 .检验工人量得 ∠BDC=143 ,就断定这个零件不合格,请你运用三角形的有关知识说明不合格的理由.如果测得 ∠BDC=145 ,能说明这个零件一定合格吗
21. 如图,在 △ABC 中,∠ABC 与 ∠ACB 的平分线相交于点 I,根据下列条件,求 ∠BIC 的度数.
(1)若 ∠ABC=60 ,∠ACB=70 ,则 ∠BIC= ;
(2)若 ∠ABC+∠ACB=130 ,则 ∠BIC= ;
(3)若 ∠A=50 ,则 ∠BIC= ;
(4)从上述计算中,我们发现 ∠A 与 ∠BIC 之间有怎样的数量关系 请说明理由.
22. 如图,已知 △ABC 中,∠ABC 的平分线与外角 ∠ACD 的平分线相交于点 I,∠A 与 ∠BIC 之间有怎样的数量关系 请说明理由.
23. 如图,在 △ABC 中,∠BAC=∠BCA,CD 平分 ∠ACB,CE⊥AB 交 AB 的延长线于点 E,若 ∠DCE=54 ,求 ∠A 的度数.
24. 如图,在 △ABC 中,分别与 ∠ABC,∠ACB 相邻的两外角的角平分线相交于点 I,∠A 与 ∠BIC 之间有怎样的数量关系 请说明理由.
答案
1. C
2. C
3. D
4. 80 ,100 ,60 ,105
5. 105
6. 120
7. 80
8. 35
9. 80 或 20
10. 240
11. 135
12. 360
13. 由题意得,∠CBD 是 △ABC 的一个外角,
∴ ∠CBD=∠ACB+∠CAD.
∴ ∠ACB=∠CBD ∠CAD=55 30 =25 .
14. (1) 正确,理由如下:
∵ ∠BCE 是 △ABC 的外角,
∴ ∠BCE=∠A+∠B,
又 ∵ ∠1 是 △CDE 的外角,
∴ ∠1=∠BCE+∠E,
∴ ∠1=∠BCE+∠E=∠A+∠B+∠E
(2) 正确,理由如下:
由 1 得,∠1=∠A+∠B+∠E,
∵ ∠B>0 ,∠E>0 ,
∴ ∠1>∠A .
15. (1) 360
(2) 如图所示.
(3) ∠1+∠2+∠3=360 ;三角形的外角和等于 360
16. ∠ADF=∠B+∠BED=30 +100 =130 ,
在 △ADF 中,∠F=180 ∠A ∠ADF=180 25 130 =25 .
17. ∵ AE 是 △ABC 的角平分线,
∴ ∠BAE=12∠BAC=12×50 =25 .
∵ CD 是 △ABC 的高,
∴ ∠ADC=90 .
∴ ∠AFC=∠DAF+∠ADF=25 +90 =115 .
18. 在 △ABD 中,
∠ABD=∠BDC ∠A=110 80 =30 ,
因为 BD 是 △ABC 的角平分线,
所以 ∠CBD=∠ABD=30 .
因为 DE∥BC,
所以 ∠EDB=∠CBD=30 .
在 △BDE 中,∠BED=180 ∠ABD ∠EDB=180 30 30 =120 .
19. 小明的理由:在 △ABC 中,外角 ∠ACF>∠BAC.
在 △ADE 中,外角 ∠BAC>∠D.
所以 ∠ACF>∠D.
小华的理由:在 △DE C 中,外角 ∠DCF>∠D.
20. 如图,连接 A D 并延长至点 E,
∠BDC=∠BDE+∠EDC=∠B+∠BAE+∠C+∠EAC=∠BAC+∠B+∠C=145 .
(1)检验工人量得 ∠BDC=143 ≠145 ,
所以零件不合格;
(2)如果测得 ∠BDC=145 ,这个零件不一定合格 .当 ∠A=90 ,∠B=35 ,∠C=20 时,∠BDC=145 ,但此零件不合格.
21. (1) 115
(2) 115
(3) 115
(4) ∠BIC=90 +12∠A.
设 ∠ABI=∠IBC=x,∠ACI=∠ICB=y,
在 △ABC 中,2x+2y=180 ∠A,
所以 x+y=90 12∠A.
在 △IBC 中,∠BIC=180 x+y=180 90 12∠A=90 +12∠A.
22. ∠BIC=12∠A,理由如下:
设 ∠ABI=∠IBC=x,∠ACI=∠ICD=y,
在 △ABC 中,2y 2x=∠A,
所以 y x=12∠A,
在 △IBC 中,∠BIC=y x=12∠A.
23. 设 ∠ACD=x .
∵CD 平分 ∠ACB,
∴∠BCD=∠ACD=x .
又 ∠BAC=∠BCA,
∴∠BAC=∠BCA=2x .
∴∠CBE=4x .
∵∠CBE+∠BCE=90 ,∠DCE=54 ,
∴4x+54 x=90 .
解得 x=12 .
∴∠A=2x=24 .
24. ∠BIC=90 12∠A.
设 ∠CBI=∠IBD=x,∠BCI=∠ICE=y,
∵△ABC 的外角和等于 360 ,
∴2x+2y+180 ∠A=360 ,
∴x+y=90 +12∠A.
在 △IBC 中,
∠BIC=180 x+y=180 90 +12∠A=90 12∠A.
