2022-2023学年华东师大版数学九年级上册23.3.4 相似三角形的应用 课时练习(含答案)
文档属性
| 名称 | 2022-2023学年华东师大版数学九年级上册23.3.4 相似三角形的应用 课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 201.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 17:25:38 | ||
图片预览



文档简介
2022-2023年华师大版数学九年级上册23.3.4
《相似三角形的应用》课时练习
一 、选择题
1.如图,为了测量池塘的宽DE,在岸边找到点C,测得CD=30 m,在DC的延长线上找一点A,测得AC=5 m,过点A作AB∥DE交EC的延长线于B,测出AB=6 m,则池塘的宽DE为( )
A.25 m B.30 m C.36 m D.40 m
2.如图,为估算学校旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
3.小明在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域离网5米的位置上,已知她的击球高度是2.4米,则她应站在离网( )
A.7.5米处 B.8米处 C.10米处 D.15米处
4.如图,铁路道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高(杆的宽度忽略不计)( )
A.4m B.6m C.8m D.12m
5.如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
A. B. C. D.
6.如图所示,某同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时尺子的刻度为12cm,已知臂长60cm,则电线杆的高度为( )
A.2.4m B.24m C.0.6m D.6m
7.如图所示的测量旗杆的方法,已知AB是标杆,BC表示AB在太阳光下的影子,叙述错误的是( )
A.可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高
B.只需测量出标杆和旗杆的影长就可计算出旗杆的高
C.可以利用△ABC∽△EDB , 来计算旗杆的高
D.需要测量出AB.BC和DB的长,才能计算出旗杆的高
8.如图,在△ABC中,D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
A.1 B.2 C.3 D.4
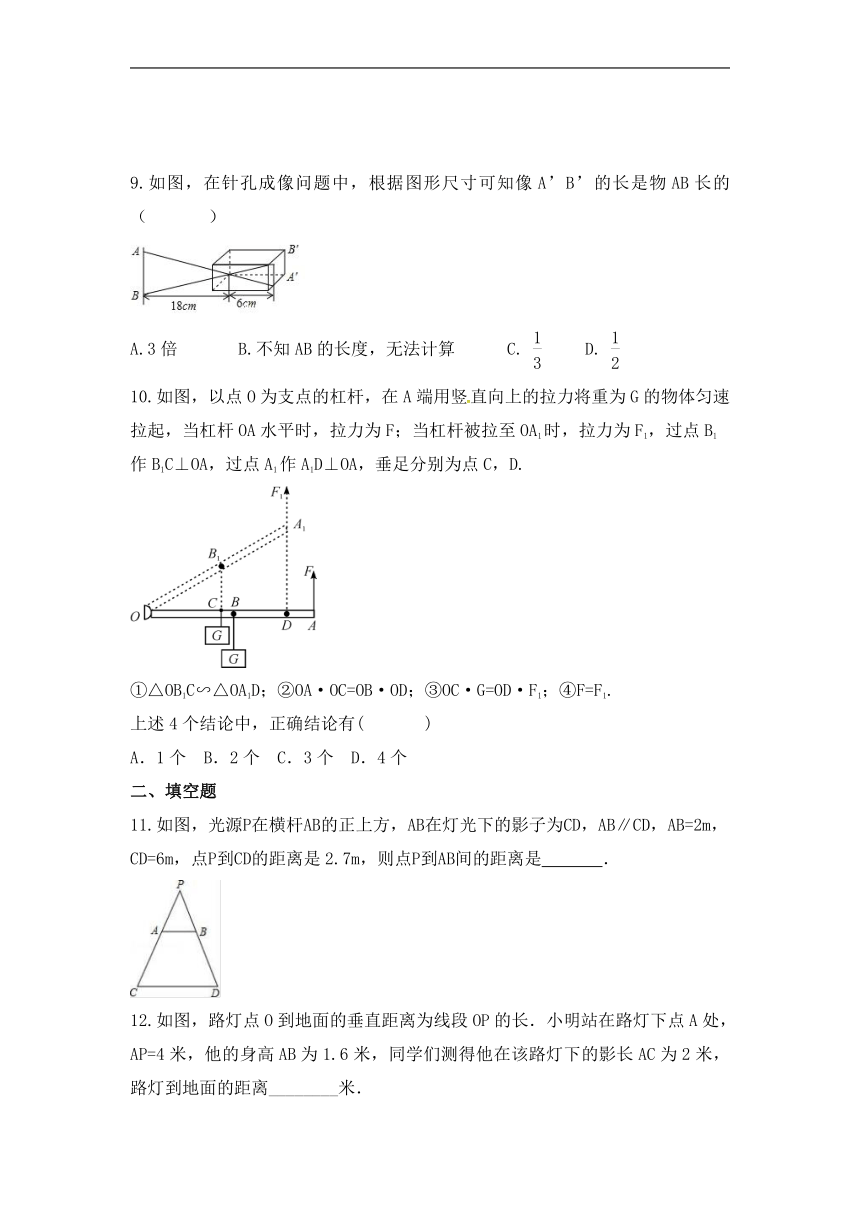
9.如图,在针孔成像问题中,根据图形尺寸可知像A’B’的长是物AB长的( )
A.3倍 B.不知AB的长度,无法计算 C. D.
10.如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1,过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C,D.
①△OB1C∽△OA1D;②OA·OC=OB·OD;③OC·G=OD·F1;④F=F1.
上述4个结论中,正确结论有( )
A.1个 B.2个 C.3个 D.4个
二 、填空题
11.如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是 .
12.如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
13.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.
14.如图,D是等边三角形ABC的边AB上一点,AD=2,BD=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E,F分别在边AC和BC上,则=________.
15.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为____.
16.如图,一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第________个.
三 、解答题
17.一位同学想利用树影测出树高,他在某时刻测得直立的标杆高1米,影长是0.9米,但他去测树影时,发现树影的上半部分落在墙CD上,(如图所示)他测得BC= 2.7米,CD=1.2米。你能帮他求出树高为多少米吗?
18.王亮同学利用课余时间对学校旗杆的高度进行测量,他是这样测量的:把长为3m的标杆垂直放置于旗杆一侧的地面上,测得标杆底端距旗杆底端的距离为15m,然后往后退,直到视线通过标杆顶端正好看不到旗杆顶端时为止,测得此时人与标杆的水平距离为2m,已知王亮的身高为1.6m,请帮他计算旗杆的高度(王亮眼睛距地面的高度视为他的身高).
19.如图,在△ABC中,D,E分别是AB,AC上的点,△ADE∽△ACB,相似比为AD∶AC=2∶3,△ABC的角平分线AF交DE于点G,交BC于点F.求AG与GF的比.
20.如图,矩形ABCD为台球桌面.AD=260 cm,AB=130 cm.球目前在E点位置,AE=60 cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点的位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
21.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图①,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1) 求证:△AEF∽△ABC;
(2) 求这个正方形零件的边长;
(3) 如果把它加工成矩形零件如图②,问这个矩形的最大面积是多少?
参考答案
1.C
2.C
3.C
4.C
5.A
6.D
7.B
8.C
9.C
10.D
11.答案为:0.9m.
12.答案为:10.
13.答案为:100
14.答案为:.
15.答案为:.
16.答案为:5
17.解:
得AB-1.2=3,
故AB=4.2米即树高为4.2米.
18.解:根据题意知,AB⊥BF,CD⊥BF,EF⊥BF,EF=1.6 m,CD=3 m,FD=2 m,BD=15 m,过E点作EH⊥AB,交AB于点H,交CD于点G,
则EG⊥CD,EH∥FB,EF=DG=BH,EG=FD,CG=CD-EF.
因为△ECG∽△EAH,
所以=,即=,
所以AH=11.9 m,
所以AB=AH+HB=AH+EF=11.9+1.6=13.5(m),即旗杆的高度为13.5 m
19.解:∵△ADE∽△ACB,
∴∠ADG=∠C.
∵AF是△ABC的角平分线,
∴∠DAG=∠FAC,
∴△ADG∽△ACF,
∴=.
∵=,∴=,
∴AG∶GF=2∶1.
20.解:(1)由题意,得∠EFG=∠DFG,
∵∠EFG+∠BFE=90°,∠DFG+∠CFD=90°,
∴∠BFE=∠CFD,∵∠B=∠C=90°,
∴△BEF∽△CDF;
(2)∵△BEF∽△CDF,
∴=,∴=,
∴CF=169.
21.解:(1)∵四边形EFHG为正方形,
∴BC∥EF,
∴△AEF∽△ABC
(2)∵四边形EFHG为正方形,
∴EF∥BC,EG⊥BC,
又∵AD⊥BC,∴EG∥AD,
设EG=EF=x,则KD=x,
∵BC=120 mm,AD=80 mm,
∴AK=80-x,
∵△AEF∽△ABC,
∴=,即=,解得x=48,
∴这个正方形零件的边长是48 mm
(3)设EG=KD=m,则AK=80-m,
∵△AEF∽△ABC,
∴=,即=,
∴EF=120-m,
∴S矩形EFHG=EG·EF=m·(120-m)=-m2+120m=-(m-40)2+2400,
故当m=40时,矩形EFHG的面积最大,最大面积为2400 mm2
《相似三角形的应用》课时练习
一 、选择题
1.如图,为了测量池塘的宽DE,在岸边找到点C,测得CD=30 m,在DC的延长线上找一点A,测得AC=5 m,过点A作AB∥DE交EC的延长线于B,测出AB=6 m,则池塘的宽DE为( )
A.25 m B.30 m C.36 m D.40 m
2.如图,为估算学校旗杆的高度,身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
3.小明在打网球时,为使球恰好能过网(网高0.8米),且落在对方区域离网5米的位置上,已知她的击球高度是2.4米,则她应站在离网( )
A.7.5米处 B.8米处 C.10米处 D.15米处
4.如图,铁路道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高(杆的宽度忽略不计)( )
A.4m B.6m C.8m D.12m
5.如图,CD是平面镜,光线从A点出发经过CD上点E反射后照到B点,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=4,CD=11,则tanα的值为( )
A. B. C. D.
6.如图所示,某同学拿着一把有刻度的尺子,站在距电线杆30m的位置,把手臂向前伸直,将尺子竖直,看到尺子遮住电线杆时尺子的刻度为12cm,已知臂长60cm,则电线杆的高度为( )
A.2.4m B.24m C.0.6m D.6m
7.如图所示的测量旗杆的方法,已知AB是标杆,BC表示AB在太阳光下的影子,叙述错误的是( )
A.可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高
B.只需测量出标杆和旗杆的影长就可计算出旗杆的高
C.可以利用△ABC∽△EDB , 来计算旗杆的高
D.需要测量出AB.BC和DB的长,才能计算出旗杆的高
8.如图,在△ABC中,D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
A.1 B.2 C.3 D.4
9.如图,在针孔成像问题中,根据图形尺寸可知像A’B’的长是物AB长的( )
A.3倍 B.不知AB的长度,无法计算 C. D.
10.如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1,过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C,D.
①△OB1C∽△OA1D;②OA·OC=OB·OD;③OC·G=OD·F1;④F=F1.
上述4个结论中,正确结论有( )
A.1个 B.2个 C.3个 D.4个
二 、填空题
11.如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则点P到AB间的距离是 .
12.如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
13.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB= m.
14.如图,D是等边三角形ABC的边AB上一点,AD=2,BD=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E,F分别在边AC和BC上,则=________.
15.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为____.
16.如图,一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第________个.
三 、解答题
17.一位同学想利用树影测出树高,他在某时刻测得直立的标杆高1米,影长是0.9米,但他去测树影时,发现树影的上半部分落在墙CD上,(如图所示)他测得BC= 2.7米,CD=1.2米。你能帮他求出树高为多少米吗?
18.王亮同学利用课余时间对学校旗杆的高度进行测量,他是这样测量的:把长为3m的标杆垂直放置于旗杆一侧的地面上,测得标杆底端距旗杆底端的距离为15m,然后往后退,直到视线通过标杆顶端正好看不到旗杆顶端时为止,测得此时人与标杆的水平距离为2m,已知王亮的身高为1.6m,请帮他计算旗杆的高度(王亮眼睛距地面的高度视为他的身高).
19.如图,在△ABC中,D,E分别是AB,AC上的点,△ADE∽△ACB,相似比为AD∶AC=2∶3,△ABC的角平分线AF交DE于点G,交BC于点F.求AG与GF的比.
20.如图,矩形ABCD为台球桌面.AD=260 cm,AB=130 cm.球目前在E点位置,AE=60 cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点的位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
21.一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图①,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1) 求证:△AEF∽△ABC;
(2) 求这个正方形零件的边长;
(3) 如果把它加工成矩形零件如图②,问这个矩形的最大面积是多少?
参考答案
1.C
2.C
3.C
4.C
5.A
6.D
7.B
8.C
9.C
10.D
11.答案为:0.9m.
12.答案为:10.
13.答案为:100
14.答案为:.
15.答案为:.
16.答案为:5
17.解:
得AB-1.2=3,
故AB=4.2米即树高为4.2米.
18.解:根据题意知,AB⊥BF,CD⊥BF,EF⊥BF,EF=1.6 m,CD=3 m,FD=2 m,BD=15 m,过E点作EH⊥AB,交AB于点H,交CD于点G,
则EG⊥CD,EH∥FB,EF=DG=BH,EG=FD,CG=CD-EF.
因为△ECG∽△EAH,
所以=,即=,
所以AH=11.9 m,
所以AB=AH+HB=AH+EF=11.9+1.6=13.5(m),即旗杆的高度为13.5 m
19.解:∵△ADE∽△ACB,
∴∠ADG=∠C.
∵AF是△ABC的角平分线,
∴∠DAG=∠FAC,
∴△ADG∽△ACF,
∴=.
∵=,∴=,
∴AG∶GF=2∶1.
20.解:(1)由题意,得∠EFG=∠DFG,
∵∠EFG+∠BFE=90°,∠DFG+∠CFD=90°,
∴∠BFE=∠CFD,∵∠B=∠C=90°,
∴△BEF∽△CDF;
(2)∵△BEF∽△CDF,
∴=,∴=,
∴CF=169.
21.解:(1)∵四边形EFHG为正方形,
∴BC∥EF,
∴△AEF∽△ABC
(2)∵四边形EFHG为正方形,
∴EF∥BC,EG⊥BC,
又∵AD⊥BC,∴EG∥AD,
设EG=EF=x,则KD=x,
∵BC=120 mm,AD=80 mm,
∴AK=80-x,
∵△AEF∽△ABC,
∴=,即=,解得x=48,
∴这个正方形零件的边长是48 mm
(3)设EG=KD=m,则AK=80-m,
∵△AEF∽△ABC,
∴=,即=,
∴EF=120-m,
∴S矩形EFHG=EG·EF=m·(120-m)=-m2+120m=-(m-40)2+2400,
故当m=40时,矩形EFHG的面积最大,最大面积为2400 mm2
