2022-2023学年苏科版数学八年级上册2.4.3角平分线的性质和判定 专项练习(含解析)
文档属性
| 名称 | 2022-2023学年苏科版数学八年级上册2.4.3角平分线的性质和判定 专项练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 749.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览

文档简介
2.4.3角平分线的性质和判定 专项练习
-2022-2023学年苏科版数学八年级上册
一、选择题
1、三角形中,到三边距离相等的点是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
2、(2022秋 瑶海区期末)如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.无法确定
3、(2022 辽宁)如图,OG平分∠MON,点A,B是射线OM,ON上的点,连接AB.按以下步骤作图:①以点B为圆心,任意长为半径作弧,交AB于点C,交BN于点D;②分别以点C和点D为圆心,大于CD长为半径作弧,两弧相交于点E;③作射线BE,交OG于点P.若∠ABN=140°,∠MON=50°,则∠OPB的度数为( )
A.35° B.45° C.55° D.65°
4、如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12 cm,则△DBE的周长为( )
A.12 cm B.11 cm C.14 cm D.10 cm
5、如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,BC=10,则PE的最小值为( )
A.8 B.5 C.4 D.2
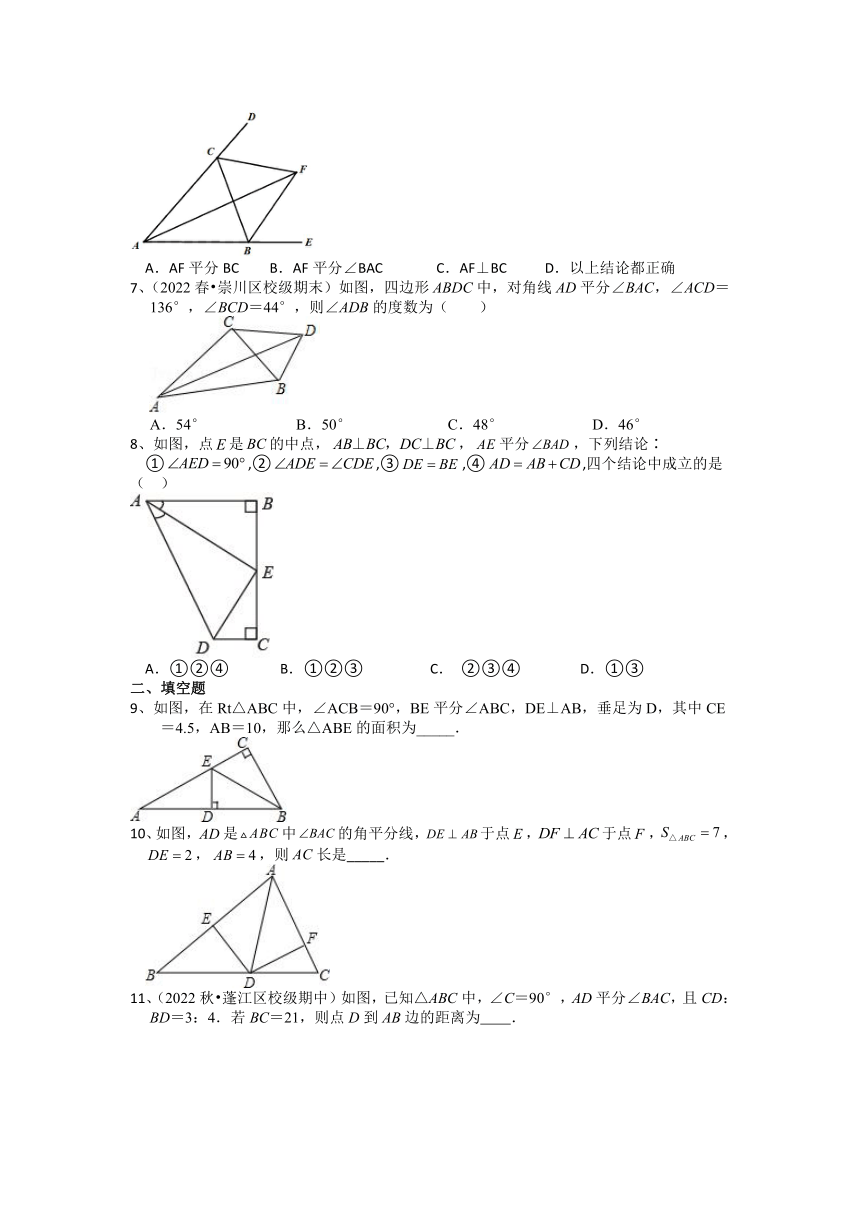
6、如图,△ABC的外角∠BCD,∠CBE的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF平分BC B.AF平分∠BAC C.AF⊥BC D.以上结论都正确
7、(2022春 崇川区校级期末)如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
8、如图,点是的中点,,平分,下列结论∶
①,②,③,④,四个结论中成立的是( )
A.①②④ B.①②③ C. ②③④ D.①③
二、填空题
9、如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,其中CE=4.5,AB=10,那么△ABE的面积为_____.
10、如图,是中的角平分线,于点,于点,,,,则长是_____.
11、(2022秋 蓬江区校级期中)如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为 .
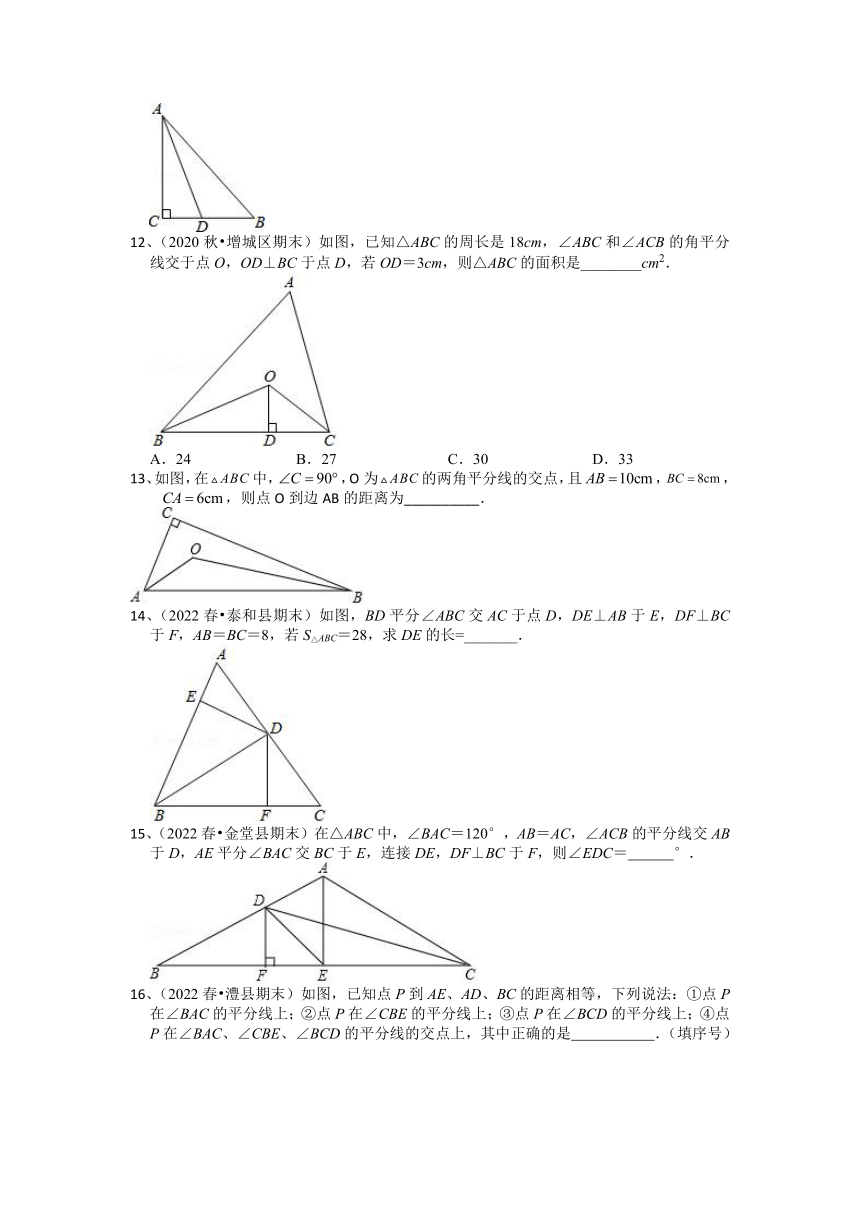
12、(2020秋 增城区期末)如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是________cm2.
A.24 B.27 C.30 D.33
13、如图,在中,,O为的两角平分线的交点,且,,,则点O到边AB的距离为__________.
14、(2022春 泰和县期末)如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=BC=8,若S△ABC=28,求DE的长=_______.
15、(2022春 金堂县期末)在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC= °.
16、(2022春 澧县期末)如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC、∠CBE、∠BCD的平分线的交点上,其中正确的是 .(填序号)
三、解答题
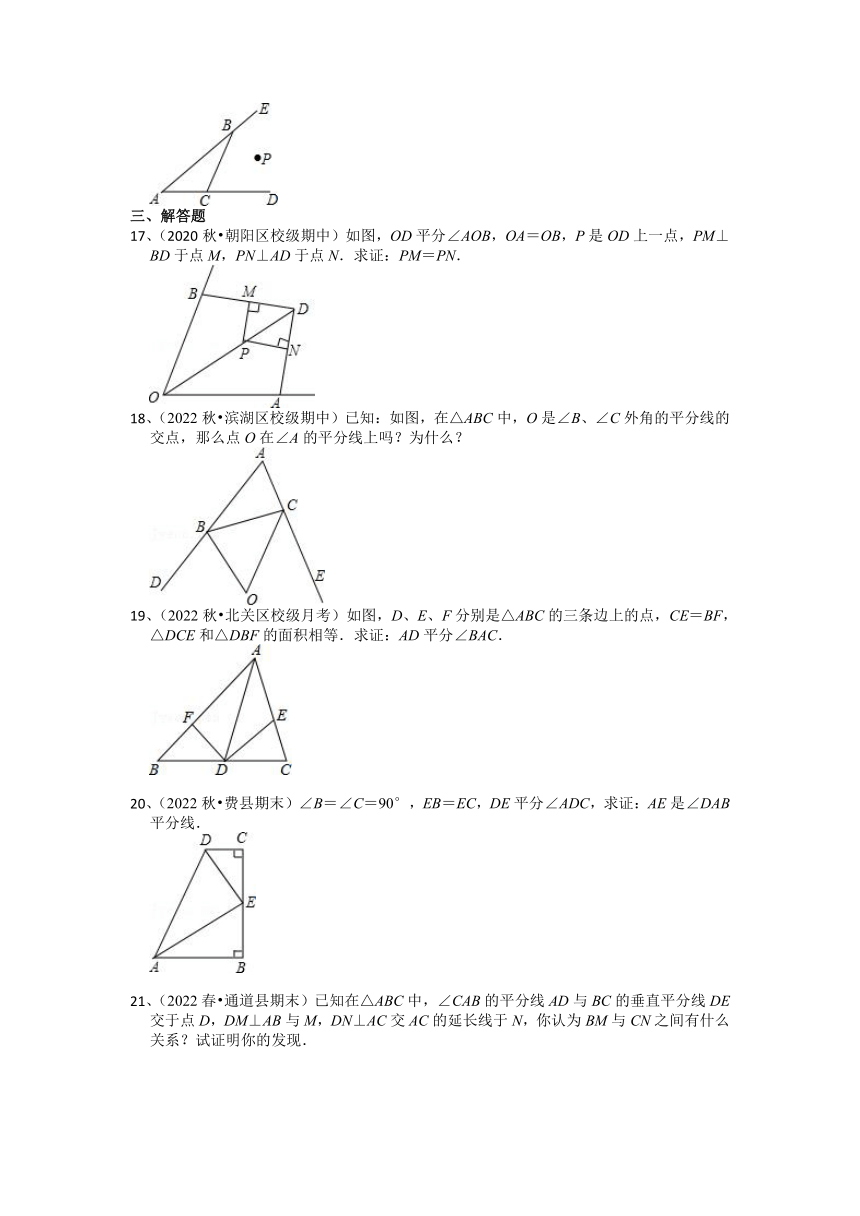
17、(2020秋 朝阳区校级期中)如图,OD平分∠AOB,OA=OB,P是OD上一点,PM⊥BD于点M,PN⊥AD于点N.求证:PM=PN.
18、(2022秋 滨湖区校级期中)已知:如图,在△ABC中,O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
19、(2022秋 北关区校级月考)如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△DBF的面积相等.求证:AD平分∠BAC.
20、(2022秋 费县期末)∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
21、(2022春 通道县期末)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB与M,DN⊥AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
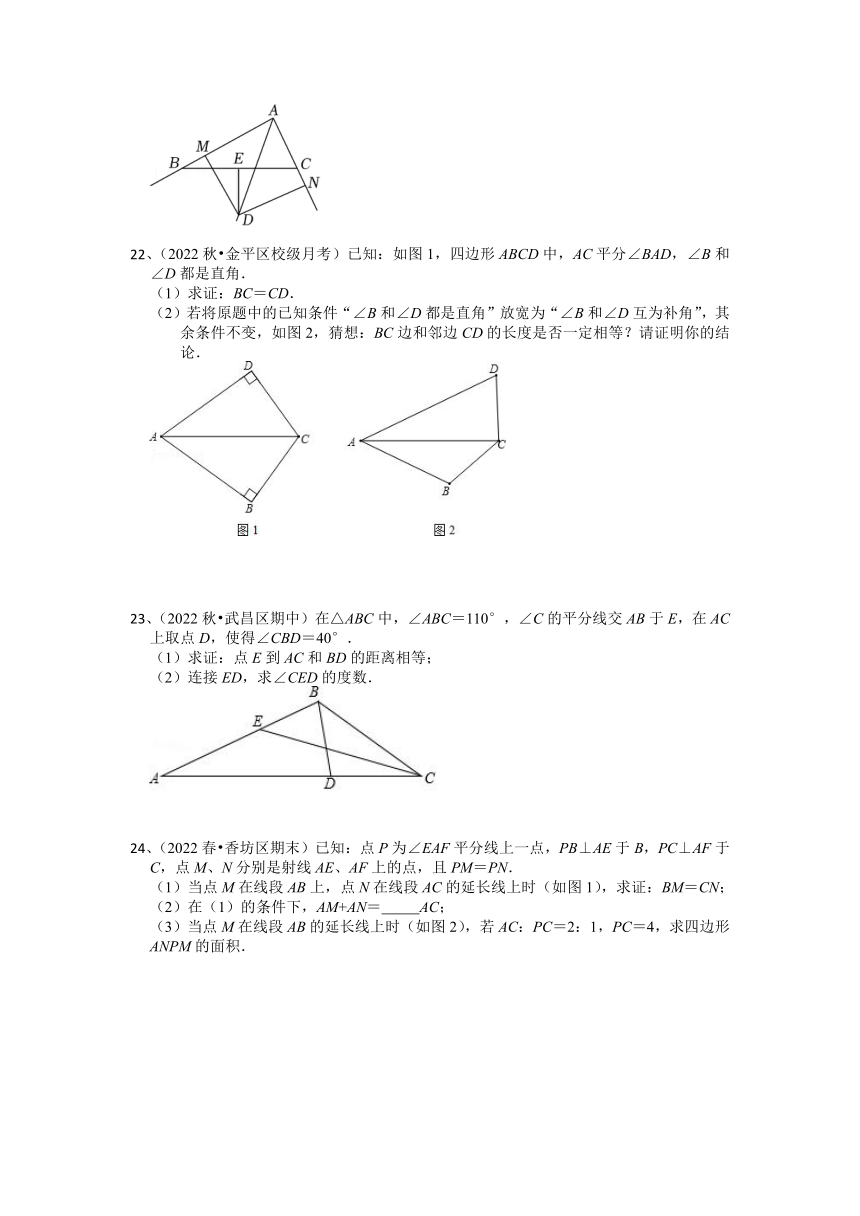
22、(2022秋 金平区校级月考)已知:如图1,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
(1)求证:BC=CD.
(2)若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变,如图2,猜想:BC边和邻边CD的长度是否一定相等?请证明你的结论.
23、(2022秋 武昌区期中)在△ABC中,∠ABC=110°,∠C的平分线交AB于E,在AC上取点D,使得∠CBD=40°.
(1)求证:点E到AC和BD的距离相等;
(2)连接ED,求∠CED的度数.
24、(2022春 香坊区期末)已知:点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,且PM=PN.
(1)当点M在线段AB上,点N在线段AC的延长线上时(如图1),求证:BM=CN;
(2)在(1)的条件下,AM+AN= AC;
(3)当点M在线段AB的延长线上时(如图2),若AC:PC=2:1,PC=4,求四边形ANPM的面积.
25、(2022秋 铁东区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
26、(2022秋 东区校级月考)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(不需证明)
(2)如图③,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
2.4.3角平分线的性质和判定 专项练习
-2022-2023学年苏科版数学八年级上册
一、选择题
1、三角形中,到三边距离相等的点是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
【解析】解:三角形中,到三边距离相等的点是三条角平分线的交点;故选C.
2、(2022秋 瑶海区期末)如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.无法确定
【解答】解:当DP⊥AB时,根据垂线段最短可知,此时DP的值最小.
由作图可知:AE平分∠BAC,
∵DC⊥AC,DP⊥AB,
∴DP=CD=2,
∴PD的最小值为2,
故选:A.
3、(2022 辽宁)如图,OG平分∠MON,点A,B是射线OM,ON上的点,连接AB.按以下步骤作图:①以点B为圆心,任意长为半径作弧,交AB于点C,交BN于点D;②分别以点C和点D为圆心,大于CD长为半径作弧,两弧相交于点E;③作射线BE,交OG于点P.若∠ABN=140°,∠MON=50°,则∠OPB的度数为( )
A.35° B.45° C.55° D.65°
【解答】解:由作法得BP平分∠ABN,
∴∠PBN=∠ABN=140°=70°,
∵OG平分∠MON,
∴∠BOP=∠MON=50°=25°,
∵∠PBN=∠POB+∠OPB,
∴∠OPB=70°﹣25°=45°.
故选:B.
4、如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12 cm,则△DBE的周长为( )
A.12 cm B.11 cm C.14 cm D.10 cm
【答案】A
【解析】∵AD是∠BAC的平分线,DE⊥AB,∠C=90°
易得△ACD≌△AED,∴CD=DE,AE=AC
∴△DBE的周长=DE+EB+BE=CD+DB+EB=BC+EB=AC+EB=AE+EB=AB=12cm.
故选A
5、如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,BC=10,则PE的最小值为( )
A.8 B.5 C.4 D.2
【答案】C
解:过E作EP⊥BC于P,此时PE的值最小,
∵AB∥CD,AD⊥AB,∴AD⊥CD,
∵BE和CE分别平分∠ABC和∠BCD,∴AE=PE,ED=PE,∴AE=ED=PE,
∵AD=8,∴PE=4,即PE的最小值是4,故选:C.
6、如图,△ABC的外角∠BCD,∠CBE的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF平分BC B.AF平分∠BAC C.AF⊥BC D.以上结论都正确
【解析】过F点分别作AB、BC、AC的垂线,垂足分别为E、G、D,
∵∠ABC、∠ACB外角的平分线相交于点F,∴EF=GF,GF=DF,
∴EF=DF,∴AF平分∠BAC.故选B
7、(2022春 崇川区校级期末)如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
【解答】解:如图所示,过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,∴DF=DE,
又∵∠ACD=136°,∠BCD=44°,∴∠ACB=92°,∠DCF=44°,∴CD平分∠BCF,
又∵DF⊥AC于F,DG⊥BC于G,∴DF=DG,∴DE=DG,
∴BD平分∠CBE,∴∠DBE=∠CBE,
∵AD平分∠BAC,∴∠BAD=∠BAC,
∴∠ADB=∠DBE﹣∠BAD=(∠CBE﹣∠BAC)=∠ACB=×92°=46°,
故选:D.
8、如图,点是的中点,,平分,下列结论∶
①,②,③,④,四个结论中成立的是( )
A.①②④ B.①②③ C. ②③④ D.①③
【答案】A
【解析】解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,∴BE=EF,AE=AE,
∴Rt△AEF≌Rt△AEB(HL),∴AB=AF,∠AEF=∠AEB;
而点E是BC的中点,∴EC=EF=BE,所以③错误;
∵EC=EF,ED=ED,∴Rt△EFD≌Rt△ECD,
∴DC=DF,∠FDE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED=∠BEC=90°,所以①正确,
综上:①②④正确,
故选:A.
二、填空题
9、如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,其中CE=4.5,AB=10,那么△ABE的面积为_____.
【答案】22.5
解:∵BE平分∠ABC,ED⊥AB,EC⊥BC,∴ED=EC=4.5,
∴S△ABE=AB·DE=×10×4.5=22.5.故答案为:22.5.
10、如图,是中的角平分线,于点,于点,,,,则长是_____.
【答案】3
【解析】解:∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∴S△ABC=×4×2+AC×2=7,
解得AC=3.故答案为:3.
11、(2022秋 蓬江区校级期中)如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为 .
【解答】解:如图,∵CD:BD=3:4.
设CD=3x,则BD=4x,∴BC=CD+BD=7x,
∵BC=21,∴7x=21,∴x=3,∴CD=9,
过点D作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,∴DE=CD=9,
∴点D到AB边的距离是9,故答案为:9.
12、(2020秋 增城区期末)如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是________cm2.
A.24 B.27 C.30 D.33
解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OACOE×AB+OD×BC+OF×AC(AB+BC+AC),
∵△ABC的周长是18,∴S△ABC×18=27(cm2).
13、如图,在中,,O为的两角平分线的交点,且,,,则点O到边AB的距离为__________.
【答案】2.
【解析】解:作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,连接OC,
∵点O为∠ABC与∠CAB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OD=OF,∴×AC×BC=×AC×OE+×BC×OF+×AB×OD,
∴×6×8=×6×OD+×8×OD+×10×OD,
解得,OD=2,即点O到边AB的距离为2,故答案为:2.
14、(2022春 泰和县期末)如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=BC=8,若S△ABC=28,求DE的长=_______.
【解答】解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,∴DE=DF,
∵S△ABC=28,AB=BC=8,∴×8×DE+×8×DF=28,∴8DE=28.∴DE=3.5.
15、(2022春 金堂县期末)在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC= °.
【解答】解:过D作DM⊥AC交CA的延长线于M,DN⊥AE,
∵CD平分∠ACB,∴DF=DM, ∵∠BAC=120°,∴∠DAM=60°,
∵AE平分∠BAC,∴∠BAE=60°,∴∠DAM=∠BAE,∴DM=DN,
∵DF⊥BC,∴DE平分∠AEB,
∵AB=AC,AE平分∠BAC交BC于E,∴AE⊥BC,∴∠AEB=90°,∴∠DEF=45°,
∵∠B=∠ACB=30°,∴∠DCF=15°,∴∠EDC=30°,故答案为:30.
16、(2022春 澧县期末)如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC、∠CBE、∠BCD的平分线的交点上,其中正确的是 .(填序号)
【解答】解:∵点P到AE、AD的距离相等,∴点P在∠BAC的平分线上,①正确;
∵点P到AE、BC的距离相等,∴点P在∠CBE的平分线上,②正确;
∵点P到AD、BC的距离相等,∴点P在∠BCD的平分线上,③正确;
∴点P在∠BAC、∠CBE、∠BCD的平分线的交点上,④正确,
故答案为:①②③④.
三、解答题
17、(2020秋 朝阳区校级期中)如图,OD平分∠AOB,OA=OB,P是OD上一点,PM⊥BD于点M,PN⊥AD于点N.求证:PM=PN.
【解答过程】证明:∵OD平分∠AOB,∴∠1=∠2.
在△OBD和△OAD中, ,∴△OBD≌△OAD(SAS).∴∠3=∠4.
∵PM⊥BD,PN⊥AD,∴PM=PN.
18、(2022秋 滨湖区校级期中)已知:如图,在△ABC中,O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
【解答】解:点O在∠A的平分线上.
理由如下:如图,过点O作OF⊥AD于F,作OG⊥BC于G,作OH⊥AE于H,
∵O是∠B、∠C外角的平分线的交点,∴OF=OG,OG=OH,
∴OF=OG=OH,∴点O在∠A的平分线上.
19、(2022秋 北关区校级月考)如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△DBF的面积相等.求证:AD平分∠BAC.
【解答】证明:过D作DN⊥AC,DM⊥AB,
△DBF的面积为:BF DM,△DCE的面积为:DN CE,
∵△DCE和△DBF的面积相等,∴BF DM=DN CE,
∵CE=BF,∴DM=DN,
又∵DM⊥AB,DN⊥AC,∴AD平分∠BAC(到角两边距离相等的点在角的平分线上).
20、(2022秋 费县期末)∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
【解答】证明:如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,∠C=90°,∴EC=EF,
∵EB=EC,∴EF=BE,
又∵∠B=90°,∴EB⊥AB,
∵EF⊥AD,∴AE是∠DAB平分线.
21、(2022春 通道县期末)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB与M,DN⊥AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
【解答】解:BM=CN.
理由:连接BD,CD,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,∴DM=DN,
∵DE垂直平分BC,∴BD=CD,
在Rt△BMD与Rt△CND中,∵,∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.
22、(2022秋 金平区校级月考)已知:如图1,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
(1)求证:BC=CD.
(2)若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变,如图2,猜想:BC边和邻边CD的长度是否一定相等?请证明你的结论.
【解答】(1)证明:∵∠D=∠B=90°,∴CD⊥AD,CB⊥AB,
∵AC平分∠BAD,∴BC=CD;
(2)解:一定相等.
证明:如图,过点C作CE⊥AD于E,作CF⊥AB于F,∴∠CBF与∠ABC互补.
∵∠B和∠D都是直角,互为补角,∴∠D=∠CBF,
又∵AC是∠BAD的平分线,∴CE=CF,
在Rt△BCF与Rt△DCE中,,∴Rt△BCF≌Rt△DCE(AAS),∴BC=CD.
23、(2022秋 武昌区期中)在△ABC中,∠ABC=110°,∠C的平分线交AB于E,在AC上取点D,使得∠CBD=40°.
(1)求证:点E到AC和BD的距离相等;
(2)连接ED,求∠CED的度数.
【解答】解:(1)延长CB至点M.
∵∠ABM=180°﹣110°=70°,∠ABM=∠ABD,∴点E到CM和BD得距离相等,
又∵CE平分平分∠ACB,∴E点到AC和BC的距离相等,
∴点E到AC和BD的距离相等;
(2)连接ED.∵点E到AC和BD的距离相等,
∴∠EDB=∠EDA; 设∠EDB=∠EDA=α,∠ACE=∠BCE=β,
又∵在△BDC中,2α=2β+40°,∴α﹣β=20°,
在△EDC中,α=β+∠DEC, 则∠CED=α﹣β=20°.
24、(2022春 香坊区期末)已知:点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,且PM=PN.
(1)当点M在线段AB上,点N在线段AC的延长线上时(如图1),求证:BM=CN;
(2)在(1)的条件下,AM+AN= AC;
(3)当点M在线段AB的延长线上时(如图2),若AC:PC=2:1,PC=4,求四边形ANPM的面积.
【解答】解:(1)∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,,∴Rt△PBM≌Rt△PCN(HL),∴BM=CN;
(2)∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,∴∠APC=∠APB,
∵PB⊥AE,PC⊥AF,∴PB=PC,
∴AM+AN=AM+CN+AC=AM+BM+AC=AB+AC=2AC;故答案为:2;
(3)∵AC:PC=2:1,PC=4,∴AC=8,∴AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB
=AC PC+AB PB=×8×4+×8×4=32.
25、(2022秋 铁东区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
【解答】(1)解:∵EF⊥AB,∠AEF=50°,∴∠FAE=90°﹣50°=40°,
∵∠BAD=100°,∴∠CAD=180°﹣100°﹣40°=40°;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,∴EF=EG,
∵BE平分∠ABC,EF⊥BF,EH⊥BC,∴EF=EH,∴EG=EH,
∵EG⊥AD,EH⊥BC,∴DE平分∠ADC;
(3)解:∵S△ACD=15,
∴AD×EG+CD×EH=15,即4×EG+8×EG=15,解得,EG=EH,
∴EF=EH,∴△ABE的面积=AB×EF=7.
26、(2022秋 东区校级月考)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(不需证明)
(2)如图③,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
【解答】解:图①如图所示;
(1)FE=FD;
(2)如图,过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,
∵AD、CE分别是∠BAC、∠BCA的平分线,∴FG=FH=FK,
在四边形BGFH中,∠GFH=360°﹣60°﹣90°×2=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,∠B=60°,
∴∠FAC+∠FCA=(180°﹣60°)=60°,
在△AFC中,∠AFC=180°﹣(∠FAC+∠FCA)=180°﹣60°=120°,
∴∠EFD=∠AFC=120°,∴∠EFG=∠DFH,
在△EFG和△DFH中,,∴△EFG≌△DFH(ASA),∴FE=FD.
-2022-2023学年苏科版数学八年级上册
一、选择题
1、三角形中,到三边距离相等的点是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
2、(2022秋 瑶海区期末)如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.无法确定
3、(2022 辽宁)如图,OG平分∠MON,点A,B是射线OM,ON上的点,连接AB.按以下步骤作图:①以点B为圆心,任意长为半径作弧,交AB于点C,交BN于点D;②分别以点C和点D为圆心,大于CD长为半径作弧,两弧相交于点E;③作射线BE,交OG于点P.若∠ABN=140°,∠MON=50°,则∠OPB的度数为( )
A.35° B.45° C.55° D.65°
4、如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12 cm,则△DBE的周长为( )
A.12 cm B.11 cm C.14 cm D.10 cm
5、如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,BC=10,则PE的最小值为( )
A.8 B.5 C.4 D.2
6、如图,△ABC的外角∠BCD,∠CBE的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF平分BC B.AF平分∠BAC C.AF⊥BC D.以上结论都正确
7、(2022春 崇川区校级期末)如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
8、如图,点是的中点,,平分,下列结论∶
①,②,③,④,四个结论中成立的是( )
A.①②④ B.①②③ C. ②③④ D.①③
二、填空题
9、如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,其中CE=4.5,AB=10,那么△ABE的面积为_____.
10、如图,是中的角平分线,于点,于点,,,,则长是_____.
11、(2022秋 蓬江区校级期中)如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为 .
12、(2020秋 增城区期末)如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是________cm2.
A.24 B.27 C.30 D.33
13、如图,在中,,O为的两角平分线的交点,且,,,则点O到边AB的距离为__________.
14、(2022春 泰和县期末)如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=BC=8,若S△ABC=28,求DE的长=_______.
15、(2022春 金堂县期末)在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC= °.
16、(2022春 澧县期末)如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC、∠CBE、∠BCD的平分线的交点上,其中正确的是 .(填序号)
三、解答题
17、(2020秋 朝阳区校级期中)如图,OD平分∠AOB,OA=OB,P是OD上一点,PM⊥BD于点M,PN⊥AD于点N.求证:PM=PN.
18、(2022秋 滨湖区校级期中)已知:如图,在△ABC中,O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
19、(2022秋 北关区校级月考)如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△DBF的面积相等.求证:AD平分∠BAC.
20、(2022秋 费县期末)∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
21、(2022春 通道县期末)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB与M,DN⊥AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
22、(2022秋 金平区校级月考)已知:如图1,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
(1)求证:BC=CD.
(2)若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变,如图2,猜想:BC边和邻边CD的长度是否一定相等?请证明你的结论.
23、(2022秋 武昌区期中)在△ABC中,∠ABC=110°,∠C的平分线交AB于E,在AC上取点D,使得∠CBD=40°.
(1)求证:点E到AC和BD的距离相等;
(2)连接ED,求∠CED的度数.
24、(2022春 香坊区期末)已知:点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,且PM=PN.
(1)当点M在线段AB上,点N在线段AC的延长线上时(如图1),求证:BM=CN;
(2)在(1)的条件下,AM+AN= AC;
(3)当点M在线段AB的延长线上时(如图2),若AC:PC=2:1,PC=4,求四边形ANPM的面积.
25、(2022秋 铁东区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
26、(2022秋 东区校级月考)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(不需证明)
(2)如图③,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
2.4.3角平分线的性质和判定 专项练习
-2022-2023学年苏科版数学八年级上册
一、选择题
1、三角形中,到三边距离相等的点是( )
A.三条高线的交点 B.三条中线的交点
C.三条角平分线的交点 D.三边垂直平分线的交点
【解析】解:三角形中,到三边距离相等的点是三条角平分线的交点;故选C.
2、(2022秋 瑶海区期末)如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=2,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.无法确定
【解答】解:当DP⊥AB时,根据垂线段最短可知,此时DP的值最小.
由作图可知:AE平分∠BAC,
∵DC⊥AC,DP⊥AB,
∴DP=CD=2,
∴PD的最小值为2,
故选:A.
3、(2022 辽宁)如图,OG平分∠MON,点A,B是射线OM,ON上的点,连接AB.按以下步骤作图:①以点B为圆心,任意长为半径作弧,交AB于点C,交BN于点D;②分别以点C和点D为圆心,大于CD长为半径作弧,两弧相交于点E;③作射线BE,交OG于点P.若∠ABN=140°,∠MON=50°,则∠OPB的度数为( )
A.35° B.45° C.55° D.65°
【解答】解:由作法得BP平分∠ABN,
∴∠PBN=∠ABN=140°=70°,
∵OG平分∠MON,
∴∠BOP=∠MON=50°=25°,
∵∠PBN=∠POB+∠OPB,
∴∠OPB=70°﹣25°=45°.
故选:B.
4、如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=12 cm,则△DBE的周长为( )
A.12 cm B.11 cm C.14 cm D.10 cm
【答案】A
【解析】∵AD是∠BAC的平分线,DE⊥AB,∠C=90°
易得△ACD≌△AED,∴CD=DE,AE=AC
∴△DBE的周长=DE+EB+BE=CD+DB+EB=BC+EB=AC+EB=AE+EB=AB=12cm.
故选A
5、如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,BC=10,则PE的最小值为( )
A.8 B.5 C.4 D.2
【答案】C
解:过E作EP⊥BC于P,此时PE的值最小,
∵AB∥CD,AD⊥AB,∴AD⊥CD,
∵BE和CE分别平分∠ABC和∠BCD,∴AE=PE,ED=PE,∴AE=ED=PE,
∵AD=8,∴PE=4,即PE的最小值是4,故选:C.
6、如图,△ABC的外角∠BCD,∠CBE的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF平分BC B.AF平分∠BAC C.AF⊥BC D.以上结论都正确
【解析】过F点分别作AB、BC、AC的垂线,垂足分别为E、G、D,
∵∠ABC、∠ACB外角的平分线相交于点F,∴EF=GF,GF=DF,
∴EF=DF,∴AF平分∠BAC.故选B
7、(2022春 崇川区校级期末)如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
【解答】解:如图所示,过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,∴DF=DE,
又∵∠ACD=136°,∠BCD=44°,∴∠ACB=92°,∠DCF=44°,∴CD平分∠BCF,
又∵DF⊥AC于F,DG⊥BC于G,∴DF=DG,∴DE=DG,
∴BD平分∠CBE,∴∠DBE=∠CBE,
∵AD平分∠BAC,∴∠BAD=∠BAC,
∴∠ADB=∠DBE﹣∠BAD=(∠CBE﹣∠BAC)=∠ACB=×92°=46°,
故选:D.
8、如图,点是的中点,,平分,下列结论∶
①,②,③,④,四个结论中成立的是( )
A.①②④ B.①②③ C. ②③④ D.①③
【答案】A
【解析】解:过E作EF⊥AD于F,如图,
∵AB⊥BC,AE平分∠BAD,∴BE=EF,AE=AE,
∴Rt△AEF≌Rt△AEB(HL),∴AB=AF,∠AEF=∠AEB;
而点E是BC的中点,∴EC=EF=BE,所以③错误;
∵EC=EF,ED=ED,∴Rt△EFD≌Rt△ECD,
∴DC=DF,∠FDE=∠CDE,所以②正确;
∴AD=AF+FD=AB+DC,所以④正确;
∴∠AED=∠AEF+∠FED=∠BEC=90°,所以①正确,
综上:①②④正确,
故选:A.
二、填空题
9、如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,其中CE=4.5,AB=10,那么△ABE的面积为_____.
【答案】22.5
解:∵BE平分∠ABC,ED⊥AB,EC⊥BC,∴ED=EC=4.5,
∴S△ABE=AB·DE=×10×4.5=22.5.故答案为:22.5.
10、如图,是中的角平分线,于点,于点,,,,则长是_____.
【答案】3
【解析】解:∵AD是△ABC中∠BAC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∴S△ABC=×4×2+AC×2=7,
解得AC=3.故答案为:3.
11、(2022秋 蓬江区校级期中)如图,已知△ABC中,∠C=90°,AD平分∠BAC,且CD:BD=3:4.若BC=21,则点D到AB边的距离为 .
【解答】解:如图,∵CD:BD=3:4.
设CD=3x,则BD=4x,∴BC=CD+BD=7x,
∵BC=21,∴7x=21,∴x=3,∴CD=9,
过点D作DE⊥AB于E,
∵AD是∠BAC的平分线,∠C=90°,∴DE=CD=9,
∴点D到AB边的距离是9,故答案为:9.
12、(2020秋 增城区期末)如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是________cm2.
A.24 B.27 C.30 D.33
解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OACOE×AB+OD×BC+OF×AC(AB+BC+AC),
∵△ABC的周长是18,∴S△ABC×18=27(cm2).
13、如图,在中,,O为的两角平分线的交点,且,,,则点O到边AB的距离为__________.
【答案】2.
【解析】解:作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,连接OC,
∵点O为∠ABC与∠CAB的平分线的交点,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OD=OF,∴×AC×BC=×AC×OE+×BC×OF+×AB×OD,
∴×6×8=×6×OD+×8×OD+×10×OD,
解得,OD=2,即点O到边AB的距离为2,故答案为:2.
14、(2022春 泰和县期末)如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=BC=8,若S△ABC=28,求DE的长=_______.
【解答】解:∵BD平分∠ABC交AC于点D,DE⊥AB,DF⊥BC,∴DE=DF,
∵S△ABC=28,AB=BC=8,∴×8×DE+×8×DF=28,∴8DE=28.∴DE=3.5.
15、(2022春 金堂县期末)在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线交AB于D,AE平分∠BAC交BC于E,连接DE,DF⊥BC于F,则∠EDC= °.
【解答】解:过D作DM⊥AC交CA的延长线于M,DN⊥AE,
∵CD平分∠ACB,∴DF=DM, ∵∠BAC=120°,∴∠DAM=60°,
∵AE平分∠BAC,∴∠BAE=60°,∴∠DAM=∠BAE,∴DM=DN,
∵DF⊥BC,∴DE平分∠AEB,
∵AB=AC,AE平分∠BAC交BC于E,∴AE⊥BC,∴∠AEB=90°,∴∠DEF=45°,
∵∠B=∠ACB=30°,∴∠DCF=15°,∴∠EDC=30°,故答案为:30.
16、(2022春 澧县期末)如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;②点P在∠CBE的平分线上;③点P在∠BCD的平分线上;④点P在∠BAC、∠CBE、∠BCD的平分线的交点上,其中正确的是 .(填序号)
【解答】解:∵点P到AE、AD的距离相等,∴点P在∠BAC的平分线上,①正确;
∵点P到AE、BC的距离相等,∴点P在∠CBE的平分线上,②正确;
∵点P到AD、BC的距离相等,∴点P在∠BCD的平分线上,③正确;
∴点P在∠BAC、∠CBE、∠BCD的平分线的交点上,④正确,
故答案为:①②③④.
三、解答题
17、(2020秋 朝阳区校级期中)如图,OD平分∠AOB,OA=OB,P是OD上一点,PM⊥BD于点M,PN⊥AD于点N.求证:PM=PN.
【解答过程】证明:∵OD平分∠AOB,∴∠1=∠2.
在△OBD和△OAD中, ,∴△OBD≌△OAD(SAS).∴∠3=∠4.
∵PM⊥BD,PN⊥AD,∴PM=PN.
18、(2022秋 滨湖区校级期中)已知:如图,在△ABC中,O是∠B、∠C外角的平分线的交点,那么点O在∠A的平分线上吗?为什么?
【解答】解:点O在∠A的平分线上.
理由如下:如图,过点O作OF⊥AD于F,作OG⊥BC于G,作OH⊥AE于H,
∵O是∠B、∠C外角的平分线的交点,∴OF=OG,OG=OH,
∴OF=OG=OH,∴点O在∠A的平分线上.
19、(2022秋 北关区校级月考)如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△DBF的面积相等.求证:AD平分∠BAC.
【解答】证明:过D作DN⊥AC,DM⊥AB,
△DBF的面积为:BF DM,△DCE的面积为:DN CE,
∵△DCE和△DBF的面积相等,∴BF DM=DN CE,
∵CE=BF,∴DM=DN,
又∵DM⊥AB,DN⊥AC,∴AD平分∠BAC(到角两边距离相等的点在角的平分线上).
20、(2022秋 费县期末)∠B=∠C=90°,EB=EC,DE平分∠ADC,求证:AE是∠DAB平分线.
【解答】证明:如图,过点E作EF⊥AD于F,
∵DE平分∠ADC,∠C=90°,∴EC=EF,
∵EB=EC,∴EF=BE,
又∵∠B=90°,∴EB⊥AB,
∵EF⊥AD,∴AE是∠DAB平分线.
21、(2022春 通道县期末)已知在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB与M,DN⊥AC交AC的延长线于N,你认为BM与CN之间有什么关系?试证明你的发现.
【解答】解:BM=CN.
理由:连接BD,CD,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,∴DM=DN,
∵DE垂直平分BC,∴BD=CD,
在Rt△BMD与Rt△CND中,∵,∴Rt△BDM≌Rt△CDN(HL),∴BM=CN.
22、(2022秋 金平区校级月考)已知:如图1,四边形ABCD中,AC平分∠BAD,∠B和∠D都是直角.
(1)求证:BC=CD.
(2)若将原题中的已知条件“∠B和∠D都是直角”放宽为“∠B和∠D互为补角”,其余条件不变,如图2,猜想:BC边和邻边CD的长度是否一定相等?请证明你的结论.
【解答】(1)证明:∵∠D=∠B=90°,∴CD⊥AD,CB⊥AB,
∵AC平分∠BAD,∴BC=CD;
(2)解:一定相等.
证明:如图,过点C作CE⊥AD于E,作CF⊥AB于F,∴∠CBF与∠ABC互补.
∵∠B和∠D都是直角,互为补角,∴∠D=∠CBF,
又∵AC是∠BAD的平分线,∴CE=CF,
在Rt△BCF与Rt△DCE中,,∴Rt△BCF≌Rt△DCE(AAS),∴BC=CD.
23、(2022秋 武昌区期中)在△ABC中,∠ABC=110°,∠C的平分线交AB于E,在AC上取点D,使得∠CBD=40°.
(1)求证:点E到AC和BD的距离相等;
(2)连接ED,求∠CED的度数.
【解答】解:(1)延长CB至点M.
∵∠ABM=180°﹣110°=70°,∠ABM=∠ABD,∴点E到CM和BD得距离相等,
又∵CE平分平分∠ACB,∴E点到AC和BC的距离相等,
∴点E到AC和BD的距离相等;
(2)连接ED.∵点E到AC和BD的距离相等,
∴∠EDB=∠EDA; 设∠EDB=∠EDA=α,∠ACE=∠BCE=β,
又∵在△BDC中,2α=2β+40°,∴α﹣β=20°,
在△EDC中,α=β+∠DEC, 则∠CED=α﹣β=20°.
24、(2022春 香坊区期末)已知:点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M、N分别是射线AE、AF上的点,且PM=PN.
(1)当点M在线段AB上,点N在线段AC的延长线上时(如图1),求证:BM=CN;
(2)在(1)的条件下,AM+AN= AC;
(3)当点M在线段AB的延长线上时(如图2),若AC:PC=2:1,PC=4,求四边形ANPM的面积.
【解答】解:(1)∵点P为∠EAF平分线上一点,PB⊥AE,PC⊥AF,
∴PB=PC,∠PBM=∠PCN=90°,
在Rt△PBM和Rt△PCN中,,∴Rt△PBM≌Rt△PCN(HL),∴BM=CN;
(2)∵∠APB=90°﹣∠PAB,∠APC=90°﹣∠PAC,∴∠APC=∠APB,
∵PB⊥AE,PC⊥AF,∴PB=PC,
∴AM+AN=AM+CN+AC=AM+BM+AC=AB+AC=2AC;故答案为:2;
(3)∵AC:PC=2:1,PC=4,∴AC=8,∴AB=AC=8,PB=PC=4,
∴S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB
=AC PC+AB PB=×8×4+×8×4=32.
25、(2022秋 铁东区校级期中)如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
【解答】(1)解:∵EF⊥AB,∠AEF=50°,∴∠FAE=90°﹣50°=40°,
∵∠BAD=100°,∴∠CAD=180°﹣100°﹣40°=40°;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,∴EF=EG,
∵BE平分∠ABC,EF⊥BF,EH⊥BC,∴EF=EH,∴EG=EH,
∵EG⊥AD,EH⊥BC,∴DE平分∠ADC;
(3)解:∵S△ACD=15,
∴AD×EG+CD×EH=15,即4×EG+8×EG=15,解得,EG=EH,
∴EF=EH,∴△ABE的面积=AB×EF=7.
26、(2022秋 东区校级月考)如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;(不需证明)
(2)如图③,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
【解答】解:图①如图所示;
(1)FE=FD;
(2)如图,过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,
∵AD、CE分别是∠BAC、∠BCA的平分线,∴FG=FH=FK,
在四边形BGFH中,∠GFH=360°﹣60°﹣90°×2=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,∠B=60°,
∴∠FAC+∠FCA=(180°﹣60°)=60°,
在△AFC中,∠AFC=180°﹣(∠FAC+∠FCA)=180°﹣60°=120°,
∴∠EFD=∠AFC=120°,∴∠EFG=∠DFH,
在△EFG和△DFH中,,∴△EFG≌△DFH(ASA),∴FE=FD.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
