数学北师大版(2019)必修第一册7.2.2古典概型的应用 教案
文档属性
| 名称 | 数学北师大版(2019)必修第一册7.2.2古典概型的应用 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 311.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 07:02:51 | ||
图片预览




文档简介
7.2.2古典概型的应用
【教学目标】
重点、难点
重点:正确理解掌握古典概型及其概率公式
难点: 古典概型中计算比较复杂的背景问题
学科素养
通过听课和独自思考过后更能体会到概率论与实际生活的密切联系;在对比学习的过程中,培养学生独立思考和对比学习的能力,使学生掌握学习的方法。理解从不同的角度考虑可以建立不同的概率模型.能够建立概率模型来解决简单的实际问题.
【知识清单】
建立不同的古典概型:
一般地,在解决实际问题中的古典概型时,对同一个古典概型,把什么看作一个________(即一次试验的结果)是人为规定的,也就是从不同的______去考虑,只要满足以下两点:
①试验中所有可能出现的基本事件只有______个,每次试验只出现其中的一个结果;
②每个试验结果出现的可能性______.
就可以将问题转化为不同的________来解决,所得可能结果越____,那么问题的解决就变得越______.
【经典例题】
题型一:概率模型的构建
【例题1】任取一个正整数,求该数的平方的末位数字是1的概率.
反思:同一个古典概型问题由于考虑的角度不同,其解法繁简差别较大,因此,在选取样本空间时,务必抓住欲求事件的本质,而把其他无关的因素抛开,以简化求解过程.
题型二:构建不同的概率模型解决问题
【例题2】袋中装有除颜色外其他均相同的6个球,其中4个白球、2个红球,从袋中任意取出两球,求下列事件的概率:
(1)A:取出的两球都是白球;
(2)B:取出的两球一个是白球,另一个是红球.
分析:求出基本事件的总数,及A,B包含的基本事件的个数,然后套用公式.
反思:用列举法把古典概型试验的基本事件一一列举出来,然后求出其中的m、n,再利用公式P(A)=求出事件A的概率,这是一个形象、直观的好方法,但列举时必须按照某种顺序,以保证做到不重复、不遗漏.
题型三:易错辨析
【例题3】有1号、2号、3号三个信箱和A,B,C,D四封信,若4封信可以任意投入信箱,投完为止,其中A信恰好投入1号或2号信箱的概率是多少?
错解:每封信投入1号信箱的机会均等,而且所有结果数为4,故A信投入1号或2号信箱的概率为+=.
错因分析:应该考虑A信投入各个信箱的概率,而错解考虑成了4封信投入某一信箱的概率.
【课堂达标】
1.在桌面上有一个正四面体.任意选取和桌面接触的平面的三边的其中一条边,以此边为轴将正四面体翻转至另一个平面,称为一次操作.如图,现底面为,且每次翻转后正四面体均在桌面上,则操作3次后,平面再度与桌面接触的概率为( )
A. B. C. D.
2.古代《冰糖葫芦》算法题:一个小摊上摆满了五彩缤纷的“冰糖葫芦”,“冰糖葫芦”制作有两种,一种是5个山楂;另一种是2个山楂、3个小桔子.若小摊上山楂共640个,小桔子共360个,现从小摊上随机选取一个“冰糖葫芦”,则这个“冰糖葫芦”是5个山楂的概率为( )
A.0.3 B.0.4 C.0.5 D.0.6
3.先后抛掷枚均匀的硬币,至少出现一次反面的概率是()
A. B. C. D.
4.中国古典乐器一般按“八音”分类.这是我国最早按乐器的制造材料来对乐器进行分类的方法,最先见于《周礼 春官 大师》,分为“金、石、土、革、丝、木、匏(páo)、竹”八音.其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器,现从“金、石、土、革、丝、木”任取“两音”,则“两音”同为打击乐器的概率为( )
A. B. C. D.
5.一张储蓄卡的密码共有6位数字,每位数字都可从0~9中任选一个.某人在银行自动取款机上取钱时,忘记了密码的最后一位数字,如果他记得密码的最后一位是偶数,则他不超过2次就按对的概率是( )
A. B. C. D.
6.孪生素数猜想是希尔伯特在1900年国际数学家大会的报告上第8个问题中提出的,其可以描述为:存在无穷多个素数p使得是素数,素数p、称为孪生素数.2013年5月,华人数学家张益唐证明了这一猜想的一个弱化形式,在孪生素数猜想的证明道路上前进了一大步.若从20以内的素数中任取两个,则其中能构成孪生素数的概率为( )
A. B. C. D.
7.袋中装有外形相同的四个小球,四个球上分别标有2,3,4,6四个数,现从袋中随机取出两个球,则两球上数字之差的绝对值不小于2的概率为( )
A. B. C. D.
8、某英语初学者在拼写单词“”时,对后三个字母的记忆有些模糊,他只记得由“”、“”、“”三个字母组成并且“”只可能在最后两个位置,如果他根据已有信息填入上述三个字母,那么他拼写正确的概率为( ).
A. B. C. D.
9.先后抛掷两枚均匀的正方体骰子(它们的各个面分别是标有点数1,2,3,4,5,6),分别用骰子朝上的面的点数组成两位数,则这个两位数是质数的概率为( )
A. B. C. D.
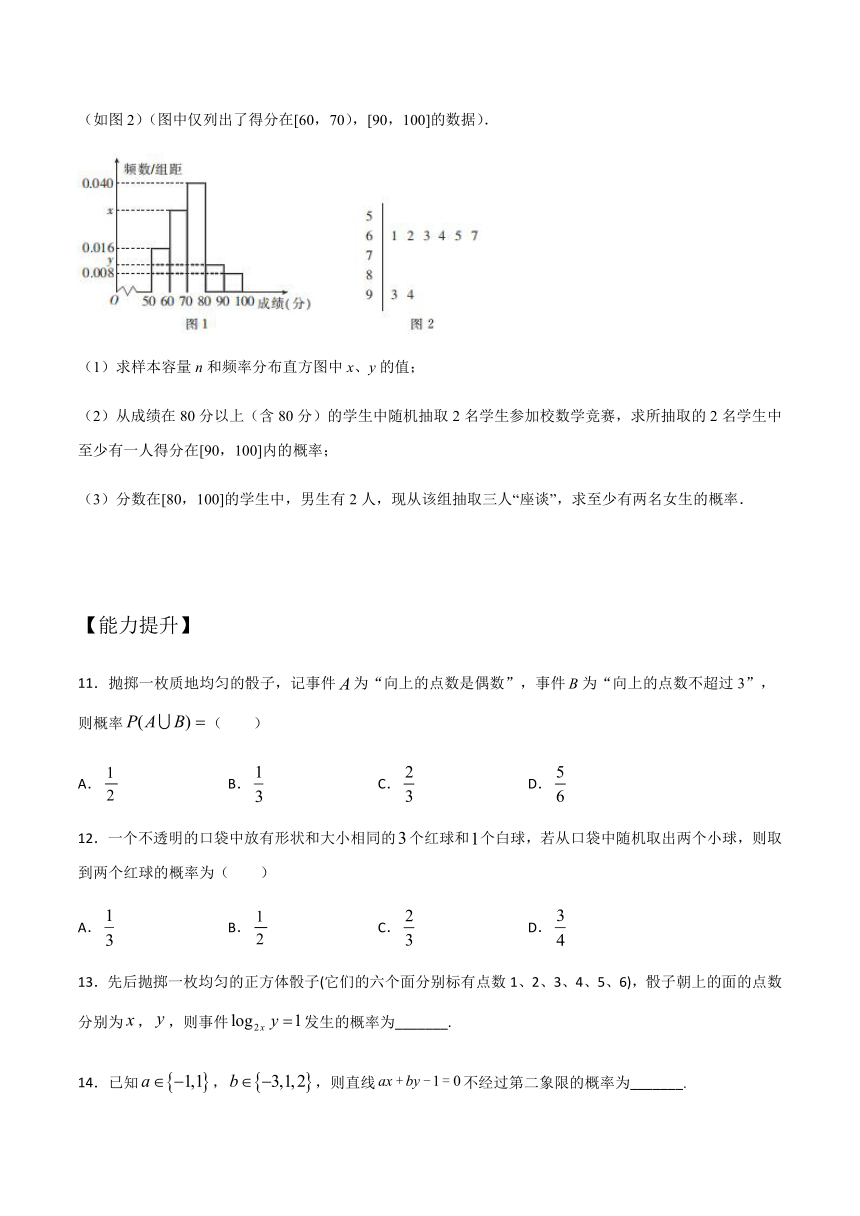
10、有n名学生,在一次数学测试后,老师将他们的分数(得分取正整数,满分为100分),按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图(如图1),并作出样本分数的茎叶图(如图2)(图中仅列出了得分在[60,70),[90,100]的数据).
(1)求样本容量n和频率分布直方图中x、y的值;
(2)从成绩在80分以上(含80分)的学生中随机抽取2名学生参加校数学竞赛,求所抽取的2名学生中至少有一人得分在[90,100]内的概率;
(3)分数在[80,100]的学生中,男生有2人,现从该组抽取三人“座谈”,求至少有两名女生的概率.
【能力提升】
11.抛掷一枚质地均匀的骰子,记事件为“向上的点数是偶数”,事件为“向上的点数不超过3”,则概率( )
A. B. C. D.
12.一个不透明的口袋中放有形状和大小相同的个红球和个白球,若从口袋中随机取出两个小球,则取到两个红球的概率为( )
A. B. C. D.
13.先后抛掷一枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为,,则事件发生的概率为_______.
14.已知,,则直线不经过第二象限的概率为_______.
15.某企业为了解该企业工人组装某产品所用时间,对每个工人组装一个该产品的用时作了记录,得到大量统计数据.从这些统计数据中随机抽取了个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过(分钟),则称这个工人为优秀员工.
(1)求这个样本数据的中位数和众数;
(2)从样本数据用时不超过分钟的工人中随机抽取个,求至少有一个工人是优秀员工的概率.
【参考答案】
【知识清单】
基本事件 角度 ①有限 ②相同 古典概型 少 简单
【例题1】解:因为正整数的个数是无限的,故不属于古典概型.但是一个正整数的平方的末位数字只取决于该正整数的末位数字,正整数的末位数字是0,1,2,…,9中的任意一个数.现任取一正整数,它的末位数字是这十个数字中的任一个是等可能出现的.因此所有的基本事件为:0,1,2,…,9,欲求的事件为1,9,即所求概率P==.
【例题2】解:设4个白球的编号为1.2.3.4,2个红球的编号为5.6.从袋中的6个球中任取两球的取法有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15种,且每种取法都是等可能发生的.
(1)从袋中的6个球中任取两球,所取的两球全是白球的取法总数,即为从4个白球中任取两球的方法总数,共有6种,即为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).所以P(A)==.
(2)从袋中的6个球中任取两球,其中一个是白球,另一个是红球的取法有(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),共8种.
所以P(B)=.
【例题3】正解:由于每封信可以任意投入信箱,对于A信,投入各个信箱的可能性是相等的,一共有3种不同的结果.投入1号信箱或2号信箱有2种结果,故A信恰好投入1号或2号信箱的概率为.
【课堂达标】
1.B
【解析】
【分析】
根据空间中两点间的距离公式结合古典概型的概率公式,即可得出答案.
【详解】
点到原点O的距离不超过3,则,即
连续掷三次骰子,得到的点的坐标共有个
其中满足条件
则点到原点O的距离不超过3的概率为
故选:B
【点睛】
本题主要考查了古典概型概率公式的应用,涉及了空间中两点间距离公式的应用,属于中档题.
1.C
【解析】
【分析】
基本事件总数为27个,满足条件的事件有6个,求出概率即可
【详解】
正四面体每个面都是三角形,每次翻转有3种选择,操作3次,
故基本事件有个,
若操作3次后平面再度与桌面接触,
第一次有3种选择,第二次有2种选择,第三次有1种选择,
故
故选:C
【点睛】
本题考查古典概型,属于基础题.
2.B
【解析】
【分析】
设5个山楂的“冰糖葫芦”有个,2个山楂、3个小桔子的“冰糖葫芦”有个,列出方程组求出,,基本事件总数,这个“冰糖葫芦”是5个山楂包含的基本事件个数,由此能求出这个“冰糖葫芦”是5个山楂的概率.
【详解】
设5个山楂的“冰糖葫芦”有个,2个山楂、3个小桔子的“冰糖葫芦”有个,
则,解得,,
基本事件总数,
这个“冰糖葫芦”是5个山楂包含的基本事件个数,
则这个“冰糖葫芦”是5个山楂的概率为.
故选:.
【点评】
本题考查概率的求法,考查古典概型等基础知识,考查运算求解能力,是基础题.
3.D
【解析】
【分析】
先求得全是正面的概率,用减去这个概率求得至少出现一次反面的概率.
【详解】
基本事件的总数为,全是正面的的事件数为,故全是正面的概率为,所以至少出现一次反面的概率为,故选D.
【点睛】
本小题主要考查古典概型概率计算,考查正难则反的思想,属于基础题.
4.B
【解析】
【分析】
由条件列举从“金、石、土、革、丝、木”中任取“两音”的所有基本事件的个数,再计算“两音”同为打击乐器所包含的所有基本事件个数,最后求其概率.
【详解】
从“金、石、土、革、丝、木”中任取“两音”,组成的基本事件包含:{金、石},{金、土},{金、革},{金、丝},{金、木},{石、土},{石、革},{石、丝},{石、木},{土、革},{土、丝},{土、木},{革、丝},{革、木},{丝、木},共15种情况,其中“两音”同为打击乐器的有{金、石},{金、革},{金、木},{石、革},{石、木},{革、木},共包含6种情况,则“两音”同为打击乐器的概率.
故选:B
【点睛】
本题考查数学文化与古典概型相结合的考查,重点考查读懂题意,属于基础题型.
5.B
【解析】
【分析】
分别求第1次就按对的概率以及第2次按对的概率,再根据概率加法得结果.
【详解】
第1次就按对的概率为
第2次按对的概率为
因此不超过2次就按对的概率是
故选:B
【点睛】
本题考查互斥事件概率加法公式,考查基本分析求解能力,属基础题.
6.C
【解析】
【分析】
根据题意20以内的素数有2,3,5,7,11,13,17,19,共8个,随机取两个,先算出基本事件总数,再找出满足孪生素数基本事件的个数,代入古典概型的概率公式求解.
【详解】
在20以内的素数有2,3,5,7,11,13,17,19,共8个,随机取两个,共有基本事件个,
满足孪生素数的有,共4个,
故概率为
故选:C.
【点睛】
本题主要考查古典概型的概率计算,属于基础题.
7.C
【解析】
【分析】
从袋中随机取出两个球,基本事件总数n=6,利用列举法求出两球上数字之差的绝对值不小于2包含的基本事件有4个,由此能求出两球上数字之差的绝对值不小于2的概率.
【详解】
现从袋中随机取出两个球,基本事件总数n=6,
两球上数字之差的绝对值不小于2包含的基本事件有:
(2,4),(2,6),(3,6),(4,6),共4个,
∴两球上数字之差的绝对值不小于2的概率为p=.
故选:C.
【点睛】
本题主要考查古典概型的概率的求法,属于基础题.
8.B
【解析】
【分析】
根据题意列举出满足题意的字母组合,即可求出结果.
【详解】
满足题意的字母组合有四种,分别是,,,,拼写正确的组合只有一种,所以概率为.
故选B.
【点睛】
本题主要考查古典概型,熟记概率计算公式即可,属于常考题型.
9.B
【解析】
【分析】
根据题意,可知抛掷骰子所得点数构成的两位数有36个,可以得到其中质数有8个,利用古典概型概率公式求得结果.
【详解】
先后抛掷两枚均匀的正方体骰子(它们的各个面分别是标有点数1,2,3,4,5,6),
分别用骰子朝上的面的点数组成两位数,共有36个,
其中质数有共8个,
所以这个两位数是质数的概率为,
故选:B.
【点睛】
该题考查的是有关概率的问题,涉及到的知识点有古典概型概率公式的应用,属于基础题目.
10.
【解析】
【分析】
基本事件的总数有种,而函数有零点必须,找到满足的种数,再利用古典概型的概率计算公式计算即可.
【详解】
由已知,函数解析式一共有种不同的情况,函数有零点,
则相应的一元二次方程的,即,所以有;;
;;;共6种情况,由古典概型的概率
计算公式可得函数有零点的概率为.
故答案为:
【点睛】
本题主要考查古典概型的概率计算,涉及到函数的零点知识,考查学生的基本计算能力,是一道容易题.
32.(1)25,0.024,0.012;(2).(3).
10,【解析】
【分析】
(1)根据成绩在[90,100]内有2人,且频率为求样本容量,由[60,70)内的频数是[90,100]的3倍求x,利用频率之和为1求y.
(2)由频率分布直方图得到成绩在[80,90]内的人数,由茎叶图得到在[90,100]内的人数,利用古典概型的概率求法,先求得从成绩在80分以上(含80分)的学生中随机抽取2名学生的基本事件总数,再得到抽取的2名学生中至少有一人得分在[90,100]内的基本事件数,代入公式求解.
(3)由(2)知[80,100]的学生共有5人,男生有2人,女生有3人,利用古典概型的概率求法,先得到从该组抽取三人的基本事件总数,再得到至少有两名女生的基本事件数,代入公式求解.
【详解】
(1)由题意得:样本容量,,
;
(2)由题意知:成绩在[80,90]内有人,设为a,b,c,在[90,100]内有2人,设为A,B,
从成绩在80分以上(含80分)的学生中随机抽取2名学生的基本事件共有10种,
所抽取的2名学生中至少有一人得分在[90,100]内的基本事件有:
共7种,
所以所抽取的2名学生中至少有一人得分在[90,100]内的概率;
(3)分数在[80,100]的学生共有5人,男生有2人,设a,b,女生有3人,设为c,d,e,
从该组抽取三人的基本事件共有10种,
至少有两名女生的基本事件有:
,共7种,
所以至少有两名女生的概率.
【点睛】
本题主要考查频率分布直方图,茎叶图,古典概型的概率,还考查了数形结合的思想和运算求解的能力,属于中档题.
【能力提升】
11.D
【解析】
【分析】
满足向上的点数是偶数或向上的点数不超过3的点数有:五种情况,得到答案.
【详解】
满足向上的点数是偶数或向上的点数不超过3的点数有:五种情况,
故.
故选:.
【点睛】
本题考查了概率的计算,意在考查学生的计算能力和应用能力.
12.B
【解析】
【分析】
将个红球分别记为、、,白球记为,列举出所有的基本事件,然后利用古典概型的概率公式可计算出所求事件的概率.
【详解】
令红球为、、,白球为,取出两个小球的所有基本事件有、、、、、,共个,其中满足条件的有个,故所求概率为.
故选:B.
【点睛】
本小题主要考查古典概率等基本知识,考查运算求解能力,应用意识,属于基础题.
13.
【解析】
试题分析:先后抛掷一枚均匀的正方体骰子,骰子朝上的面的点数的所有可能情况有种,而满足即的情况有:,,共三种情况,故所求的概率为.
考点:1.古典概率;2.对数的运算.
14.
【解析】
【分析】
包含的基本事件总数,直线不经过第二象限,从而
,,由此利用列举法能求出直线不经过第二象限的概率.
【详解】
直线:,若,,
包含的基本事件总数,
直线不经过第二象限,
,,
满足直线不经过第二象限的有:,共种情况.
直线不经过第二象限的概率为.
故答案为:
【点睛】
本题考查了古典概型的概率计算公式,列举法求基本事件个数,属于综合题
15.(1)中位数为,众数为47.(2)
【解析】
【分析】
(1)茎叶图完全反映所有的原始数据,由茎叶图直接得中位数43,众数47
(2)用列举法得到用时不超过分钟的工人中随机抽取个的基本事件总数为21种,和所求至少有一个工人是优秀员工的基本事件数为15种,利用古典概型的概率公式计算可得.
【详解】
解:由茎叶图得:
中位数为,众数为.
设不超过的工人为,
其中为优秀员工,
从这名工人中随机抽取人的基本事件有个,分别为:
其中至少有一名工人是优秀员工的基本事件有个,
至少有一个工人是优秀员工的概率.
【点睛】
本题考查利用茎叶图中位数和众数问题及古典概型的概率. 解决古典概型实际问题的步骤:
(1)判断是否是古典概型,(2)列举或计算基本事件总数和所求基本事件数(3)用古典概型的概率公式计算
【教学目标】
重点、难点
重点:正确理解掌握古典概型及其概率公式
难点: 古典概型中计算比较复杂的背景问题
学科素养
通过听课和独自思考过后更能体会到概率论与实际生活的密切联系;在对比学习的过程中,培养学生独立思考和对比学习的能力,使学生掌握学习的方法。理解从不同的角度考虑可以建立不同的概率模型.能够建立概率模型来解决简单的实际问题.
【知识清单】
建立不同的古典概型:
一般地,在解决实际问题中的古典概型时,对同一个古典概型,把什么看作一个________(即一次试验的结果)是人为规定的,也就是从不同的______去考虑,只要满足以下两点:
①试验中所有可能出现的基本事件只有______个,每次试验只出现其中的一个结果;
②每个试验结果出现的可能性______.
就可以将问题转化为不同的________来解决,所得可能结果越____,那么问题的解决就变得越______.
【经典例题】
题型一:概率模型的构建
【例题1】任取一个正整数,求该数的平方的末位数字是1的概率.
反思:同一个古典概型问题由于考虑的角度不同,其解法繁简差别较大,因此,在选取样本空间时,务必抓住欲求事件的本质,而把其他无关的因素抛开,以简化求解过程.
题型二:构建不同的概率模型解决问题
【例题2】袋中装有除颜色外其他均相同的6个球,其中4个白球、2个红球,从袋中任意取出两球,求下列事件的概率:
(1)A:取出的两球都是白球;
(2)B:取出的两球一个是白球,另一个是红球.
分析:求出基本事件的总数,及A,B包含的基本事件的个数,然后套用公式.
反思:用列举法把古典概型试验的基本事件一一列举出来,然后求出其中的m、n,再利用公式P(A)=求出事件A的概率,这是一个形象、直观的好方法,但列举时必须按照某种顺序,以保证做到不重复、不遗漏.
题型三:易错辨析
【例题3】有1号、2号、3号三个信箱和A,B,C,D四封信,若4封信可以任意投入信箱,投完为止,其中A信恰好投入1号或2号信箱的概率是多少?
错解:每封信投入1号信箱的机会均等,而且所有结果数为4,故A信投入1号或2号信箱的概率为+=.
错因分析:应该考虑A信投入各个信箱的概率,而错解考虑成了4封信投入某一信箱的概率.
【课堂达标】
1.在桌面上有一个正四面体.任意选取和桌面接触的平面的三边的其中一条边,以此边为轴将正四面体翻转至另一个平面,称为一次操作.如图,现底面为,且每次翻转后正四面体均在桌面上,则操作3次后,平面再度与桌面接触的概率为( )
A. B. C. D.
2.古代《冰糖葫芦》算法题:一个小摊上摆满了五彩缤纷的“冰糖葫芦”,“冰糖葫芦”制作有两种,一种是5个山楂;另一种是2个山楂、3个小桔子.若小摊上山楂共640个,小桔子共360个,现从小摊上随机选取一个“冰糖葫芦”,则这个“冰糖葫芦”是5个山楂的概率为( )
A.0.3 B.0.4 C.0.5 D.0.6
3.先后抛掷枚均匀的硬币,至少出现一次反面的概率是()
A. B. C. D.
4.中国古典乐器一般按“八音”分类.这是我国最早按乐器的制造材料来对乐器进行分类的方法,最先见于《周礼 春官 大师》,分为“金、石、土、革、丝、木、匏(páo)、竹”八音.其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器,现从“金、石、土、革、丝、木”任取“两音”,则“两音”同为打击乐器的概率为( )
A. B. C. D.
5.一张储蓄卡的密码共有6位数字,每位数字都可从0~9中任选一个.某人在银行自动取款机上取钱时,忘记了密码的最后一位数字,如果他记得密码的最后一位是偶数,则他不超过2次就按对的概率是( )
A. B. C. D.
6.孪生素数猜想是希尔伯特在1900年国际数学家大会的报告上第8个问题中提出的,其可以描述为:存在无穷多个素数p使得是素数,素数p、称为孪生素数.2013年5月,华人数学家张益唐证明了这一猜想的一个弱化形式,在孪生素数猜想的证明道路上前进了一大步.若从20以内的素数中任取两个,则其中能构成孪生素数的概率为( )
A. B. C. D.
7.袋中装有外形相同的四个小球,四个球上分别标有2,3,4,6四个数,现从袋中随机取出两个球,则两球上数字之差的绝对值不小于2的概率为( )
A. B. C. D.
8、某英语初学者在拼写单词“”时,对后三个字母的记忆有些模糊,他只记得由“”、“”、“”三个字母组成并且“”只可能在最后两个位置,如果他根据已有信息填入上述三个字母,那么他拼写正确的概率为( ).
A. B. C. D.
9.先后抛掷两枚均匀的正方体骰子(它们的各个面分别是标有点数1,2,3,4,5,6),分别用骰子朝上的面的点数组成两位数,则这个两位数是质数的概率为( )
A. B. C. D.
10、有n名学生,在一次数学测试后,老师将他们的分数(得分取正整数,满分为100分),按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图(如图1),并作出样本分数的茎叶图(如图2)(图中仅列出了得分在[60,70),[90,100]的数据).
(1)求样本容量n和频率分布直方图中x、y的值;
(2)从成绩在80分以上(含80分)的学生中随机抽取2名学生参加校数学竞赛,求所抽取的2名学生中至少有一人得分在[90,100]内的概率;
(3)分数在[80,100]的学生中,男生有2人,现从该组抽取三人“座谈”,求至少有两名女生的概率.
【能力提升】
11.抛掷一枚质地均匀的骰子,记事件为“向上的点数是偶数”,事件为“向上的点数不超过3”,则概率( )
A. B. C. D.
12.一个不透明的口袋中放有形状和大小相同的个红球和个白球,若从口袋中随机取出两个小球,则取到两个红球的概率为( )
A. B. C. D.
13.先后抛掷一枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为,,则事件发生的概率为_______.
14.已知,,则直线不经过第二象限的概率为_______.
15.某企业为了解该企业工人组装某产品所用时间,对每个工人组装一个该产品的用时作了记录,得到大量统计数据.从这些统计数据中随机抽取了个数据作为样本,得到如图所示的茎叶图(单位:分钟).若用时不超过(分钟),则称这个工人为优秀员工.
(1)求这个样本数据的中位数和众数;
(2)从样本数据用时不超过分钟的工人中随机抽取个,求至少有一个工人是优秀员工的概率.
【参考答案】
【知识清单】
基本事件 角度 ①有限 ②相同 古典概型 少 简单
【例题1】解:因为正整数的个数是无限的,故不属于古典概型.但是一个正整数的平方的末位数字只取决于该正整数的末位数字,正整数的末位数字是0,1,2,…,9中的任意一个数.现任取一正整数,它的末位数字是这十个数字中的任一个是等可能出现的.因此所有的基本事件为:0,1,2,…,9,欲求的事件为1,9,即所求概率P==.
【例题2】解:设4个白球的编号为1.2.3.4,2个红球的编号为5.6.从袋中的6个球中任取两球的取法有:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15种,且每种取法都是等可能发生的.
(1)从袋中的6个球中任取两球,所取的两球全是白球的取法总数,即为从4个白球中任取两球的方法总数,共有6种,即为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).所以P(A)==.
(2)从袋中的6个球中任取两球,其中一个是白球,另一个是红球的取法有(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),共8种.
所以P(B)=.
【例题3】正解:由于每封信可以任意投入信箱,对于A信,投入各个信箱的可能性是相等的,一共有3种不同的结果.投入1号信箱或2号信箱有2种结果,故A信恰好投入1号或2号信箱的概率为.
【课堂达标】
1.B
【解析】
【分析】
根据空间中两点间的距离公式结合古典概型的概率公式,即可得出答案.
【详解】
点到原点O的距离不超过3,则,即
连续掷三次骰子,得到的点的坐标共有个
其中满足条件
则点到原点O的距离不超过3的概率为
故选:B
【点睛】
本题主要考查了古典概型概率公式的应用,涉及了空间中两点间距离公式的应用,属于中档题.
1.C
【解析】
【分析】
基本事件总数为27个,满足条件的事件有6个,求出概率即可
【详解】
正四面体每个面都是三角形,每次翻转有3种选择,操作3次,
故基本事件有个,
若操作3次后平面再度与桌面接触,
第一次有3种选择,第二次有2种选择,第三次有1种选择,
故
故选:C
【点睛】
本题考查古典概型,属于基础题.
2.B
【解析】
【分析】
设5个山楂的“冰糖葫芦”有个,2个山楂、3个小桔子的“冰糖葫芦”有个,列出方程组求出,,基本事件总数,这个“冰糖葫芦”是5个山楂包含的基本事件个数,由此能求出这个“冰糖葫芦”是5个山楂的概率.
【详解】
设5个山楂的“冰糖葫芦”有个,2个山楂、3个小桔子的“冰糖葫芦”有个,
则,解得,,
基本事件总数,
这个“冰糖葫芦”是5个山楂包含的基本事件个数,
则这个“冰糖葫芦”是5个山楂的概率为.
故选:.
【点评】
本题考查概率的求法,考查古典概型等基础知识,考查运算求解能力,是基础题.
3.D
【解析】
【分析】
先求得全是正面的概率,用减去这个概率求得至少出现一次反面的概率.
【详解】
基本事件的总数为,全是正面的的事件数为,故全是正面的概率为,所以至少出现一次反面的概率为,故选D.
【点睛】
本小题主要考查古典概型概率计算,考查正难则反的思想,属于基础题.
4.B
【解析】
【分析】
由条件列举从“金、石、土、革、丝、木”中任取“两音”的所有基本事件的个数,再计算“两音”同为打击乐器所包含的所有基本事件个数,最后求其概率.
【详解】
从“金、石、土、革、丝、木”中任取“两音”,组成的基本事件包含:{金、石},{金、土},{金、革},{金、丝},{金、木},{石、土},{石、革},{石、丝},{石、木},{土、革},{土、丝},{土、木},{革、丝},{革、木},{丝、木},共15种情况,其中“两音”同为打击乐器的有{金、石},{金、革},{金、木},{石、革},{石、木},{革、木},共包含6种情况,则“两音”同为打击乐器的概率.
故选:B
【点睛】
本题考查数学文化与古典概型相结合的考查,重点考查读懂题意,属于基础题型.
5.B
【解析】
【分析】
分别求第1次就按对的概率以及第2次按对的概率,再根据概率加法得结果.
【详解】
第1次就按对的概率为
第2次按对的概率为
因此不超过2次就按对的概率是
故选:B
【点睛】
本题考查互斥事件概率加法公式,考查基本分析求解能力,属基础题.
6.C
【解析】
【分析】
根据题意20以内的素数有2,3,5,7,11,13,17,19,共8个,随机取两个,先算出基本事件总数,再找出满足孪生素数基本事件的个数,代入古典概型的概率公式求解.
【详解】
在20以内的素数有2,3,5,7,11,13,17,19,共8个,随机取两个,共有基本事件个,
满足孪生素数的有,共4个,
故概率为
故选:C.
【点睛】
本题主要考查古典概型的概率计算,属于基础题.
7.C
【解析】
【分析】
从袋中随机取出两个球,基本事件总数n=6,利用列举法求出两球上数字之差的绝对值不小于2包含的基本事件有4个,由此能求出两球上数字之差的绝对值不小于2的概率.
【详解】
现从袋中随机取出两个球,基本事件总数n=6,
两球上数字之差的绝对值不小于2包含的基本事件有:
(2,4),(2,6),(3,6),(4,6),共4个,
∴两球上数字之差的绝对值不小于2的概率为p=.
故选:C.
【点睛】
本题主要考查古典概型的概率的求法,属于基础题.
8.B
【解析】
【分析】
根据题意列举出满足题意的字母组合,即可求出结果.
【详解】
满足题意的字母组合有四种,分别是,,,,拼写正确的组合只有一种,所以概率为.
故选B.
【点睛】
本题主要考查古典概型,熟记概率计算公式即可,属于常考题型.
9.B
【解析】
【分析】
根据题意,可知抛掷骰子所得点数构成的两位数有36个,可以得到其中质数有8个,利用古典概型概率公式求得结果.
【详解】
先后抛掷两枚均匀的正方体骰子(它们的各个面分别是标有点数1,2,3,4,5,6),
分别用骰子朝上的面的点数组成两位数,共有36个,
其中质数有共8个,
所以这个两位数是质数的概率为,
故选:B.
【点睛】
该题考查的是有关概率的问题,涉及到的知识点有古典概型概率公式的应用,属于基础题目.
10.
【解析】
【分析】
基本事件的总数有种,而函数有零点必须,找到满足的种数,再利用古典概型的概率计算公式计算即可.
【详解】
由已知,函数解析式一共有种不同的情况,函数有零点,
则相应的一元二次方程的,即,所以有;;
;;;共6种情况,由古典概型的概率
计算公式可得函数有零点的概率为.
故答案为:
【点睛】
本题主要考查古典概型的概率计算,涉及到函数的零点知识,考查学生的基本计算能力,是一道容易题.
32.(1)25,0.024,0.012;(2).(3).
10,【解析】
【分析】
(1)根据成绩在[90,100]内有2人,且频率为求样本容量,由[60,70)内的频数是[90,100]的3倍求x,利用频率之和为1求y.
(2)由频率分布直方图得到成绩在[80,90]内的人数,由茎叶图得到在[90,100]内的人数,利用古典概型的概率求法,先求得从成绩在80分以上(含80分)的学生中随机抽取2名学生的基本事件总数,再得到抽取的2名学生中至少有一人得分在[90,100]内的基本事件数,代入公式求解.
(3)由(2)知[80,100]的学生共有5人,男生有2人,女生有3人,利用古典概型的概率求法,先得到从该组抽取三人的基本事件总数,再得到至少有两名女生的基本事件数,代入公式求解.
【详解】
(1)由题意得:样本容量,,
;
(2)由题意知:成绩在[80,90]内有人,设为a,b,c,在[90,100]内有2人,设为A,B,
从成绩在80分以上(含80分)的学生中随机抽取2名学生的基本事件共有10种,
所抽取的2名学生中至少有一人得分在[90,100]内的基本事件有:
共7种,
所以所抽取的2名学生中至少有一人得分在[90,100]内的概率;
(3)分数在[80,100]的学生共有5人,男生有2人,设a,b,女生有3人,设为c,d,e,
从该组抽取三人的基本事件共有10种,
至少有两名女生的基本事件有:
,共7种,
所以至少有两名女生的概率.
【点睛】
本题主要考查频率分布直方图,茎叶图,古典概型的概率,还考查了数形结合的思想和运算求解的能力,属于中档题.
【能力提升】
11.D
【解析】
【分析】
满足向上的点数是偶数或向上的点数不超过3的点数有:五种情况,得到答案.
【详解】
满足向上的点数是偶数或向上的点数不超过3的点数有:五种情况,
故.
故选:.
【点睛】
本题考查了概率的计算,意在考查学生的计算能力和应用能力.
12.B
【解析】
【分析】
将个红球分别记为、、,白球记为,列举出所有的基本事件,然后利用古典概型的概率公式可计算出所求事件的概率.
【详解】
令红球为、、,白球为,取出两个小球的所有基本事件有、、、、、,共个,其中满足条件的有个,故所求概率为.
故选:B.
【点睛】
本小题主要考查古典概率等基本知识,考查运算求解能力,应用意识,属于基础题.
13.
【解析】
试题分析:先后抛掷一枚均匀的正方体骰子,骰子朝上的面的点数的所有可能情况有种,而满足即的情况有:,,共三种情况,故所求的概率为.
考点:1.古典概率;2.对数的运算.
14.
【解析】
【分析】
包含的基本事件总数,直线不经过第二象限,从而
,,由此利用列举法能求出直线不经过第二象限的概率.
【详解】
直线:,若,,
包含的基本事件总数,
直线不经过第二象限,
,,
满足直线不经过第二象限的有:,共种情况.
直线不经过第二象限的概率为.
故答案为:
【点睛】
本题考查了古典概型的概率计算公式,列举法求基本事件个数,属于综合题
15.(1)中位数为,众数为47.(2)
【解析】
【分析】
(1)茎叶图完全反映所有的原始数据,由茎叶图直接得中位数43,众数47
(2)用列举法得到用时不超过分钟的工人中随机抽取个的基本事件总数为21种,和所求至少有一个工人是优秀员工的基本事件数为15种,利用古典概型的概率公式计算可得.
【详解】
解:由茎叶图得:
中位数为,众数为.
设不超过的工人为,
其中为优秀员工,
从这名工人中随机抽取人的基本事件有个,分别为:
其中至少有一名工人是优秀员工的基本事件有个,
至少有一个工人是优秀员工的概率.
【点睛】
本题考查利用茎叶图中位数和众数问题及古典概型的概率. 解决古典概型实际问题的步骤:
(1)判断是否是古典概型,(2)列举或计算基本事件总数和所求基本事件数(3)用古典概型的概率公式计算
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
