数学北师大版(2019)必修第一册6.4.3百分位数 教案
文档属性
| 名称 | 数学北师大版(2019)必修第一册6.4.3百分位数 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 07:06:10 | ||
图片预览




文档简介
6.4.3百分位数
【教学目标】
重点、难点
重点:样本众数、中位数、平均数的意义及求法,实际问题中三数的应用。
难点:比较复杂的百分数应用题
学科素养
通过对有关数据的收集、整理、分析、判断培养学生“实事求是”的科学态度。
【知识清单】
1 .频率分布表、频率分布直方图的制作步骤及意义
2 .百分位数
(1) 定义:一般地,一组数据的第 p 百分位数是这样一个值,它使得这组数据中至少有 p % 的数据小于或等于这个值,且至少有 (100 - p )% 的数据大于或等于这个值.
(2) 计算步骤:计算一组 n 个数据的第 p 百分位数的步骤:
第 1 步,按 从小到大 排列原始数据.
第 2 步,计算 i = n × p % .
第 3 步,若 i 不是整数,而大于 i 的比邻整数为 j ,则第 p 百分位数为第 j 项数据;若 i 是整数,则第 p 百分位数为第 i 项与第 ( i + 1) 项数据的 平均数 .
【经典例题】
例1. 高二 (1) 班 7 人宿舍中每个同学的身高分别为 170,168,172,172,175,176,180 ,求这 7 人的第 40 的百分位数为 ( )
A . 168 B . 170
C . 172 D . 171
例2 .某中学高二 (2) 班甲、乙两名学生自进入高中以来,每次数学考试成绩情况如下:
甲: 95,81,75,91,86,89,71,65,76,88,94,110,107.
乙: 83,86,93,99,88,103,98,114,98,79,78,106,101.
计算出学生甲、乙的 25% 分位数和 50% 分位数.
例3 . ( 学科素养 — 数据处理 ) 某风景区对 5 个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变.有关数据如表所示:
景点 A B C D E
原价 ( 元 ) 10 10 15 20 25
现价 ( 元 ) 5 5 15 25 30
日平均人数 ( 千人 ) 1 1 2 3 2
(1) 该风景区称调整前后这 5 个景点门票的平均收费不变,日平均总收入持平.问风景区是怎样计算的?
(2) 另一方面,游客认为调整收费后风景区的日平均总收入相对于调价前,实际上增加了约 9.4%. 问游客是怎样计算的?
(3) 你认为风景区和游客哪一个的说法较能反映整体实际?
【课堂达标】
1.以下数据为参加数学竞赛决赛的人的成绩:(单位:分)、、、、、、、、、、、、、、,则这人成绩的第百分位数是( )
A. B. C. D.
2.高二(1)班7人宿舍中每个同学的身高分别为170,168,172,172,175,176,180,求这7人的第60百分位数为( )
A.168 B.175 C.172 D.176
3.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近表示满意度越高.现随机抽取位北京市民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的分位数是( )
A.7 B. C.8 D.
4.2021年起,我市将试行“3+1+2”的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
A.甲的化学成绩领先年级平均分最多.
B.甲有2个科目的成绩低于年级平均分.
C.甲的成绩最好的前两个科目是化学和地理.
D.对甲而言,物理、化学、地理是比较理想的一种选科结果.
5.以下数据为参加数学竞赛决赛的15人的成绩:
78,70,72,86,88,79,80,81,94,84,56,98,83,90,91,
则这15人成绩的第80百分位是( )
A.90 B.90.5 C.91 D.91.5
6.为做好“新冠肺炎”疫情肪控工作,济南市各学校坚持落实“双测温两报告”制度,以下是某宿舍6名同学某日上午的体温记录:36.3,36.1,36.4,36.7,36.5,36.6(单位:),则该组数据的第80百分位数为________.
7.数据:18,26,27,28,30,32,34,40的75%分位数为______.
【能力提升】
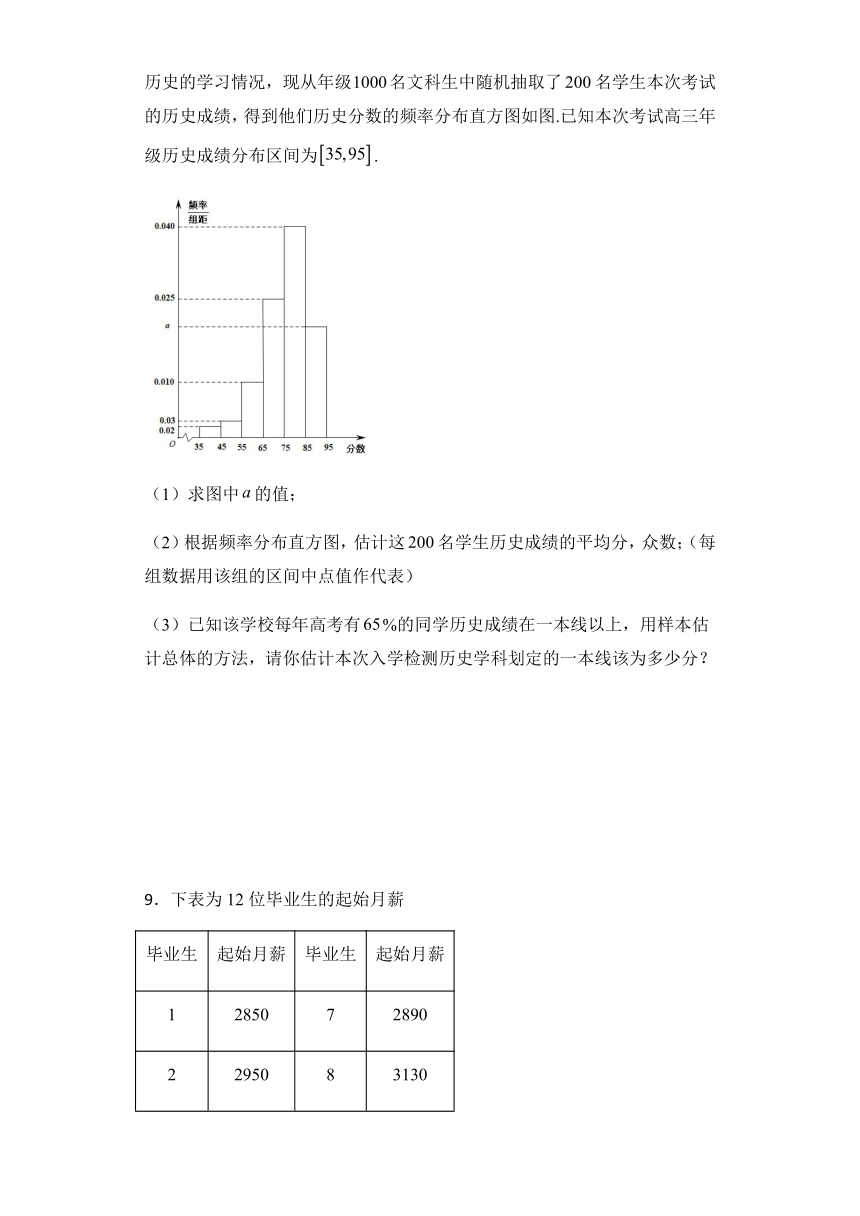
8.某学校高三年级在开学时举行了入学检测.为了了解本年级学生寒假期间历史的学习情况,现从年级名文科生中随机抽取了名学生本次考试的历史成绩,得到他们历史分数的频率分布直方图如图.已知本次考试高三年级历史成绩分布区间为.
(1)求图中的值;
(2)根据频率分布直方图,估计这名学生历史成绩的平均分,众数;(每组数据用该组的区间中点值作代表)
(3)已知该学校每年高考有%的同学历史成绩在一本线以上,用样本估计总体的方法,请你估计本次入学检测历史学科划定的一本线该为多少分?
9.下表为12位毕业生的起始月薪
毕业生 起始月薪 毕业生 起始月薪
1 2850 7 2890
2 2950 8 3130
3 3050 9 2940
4 2880 10 3325
5 2755 11 2920
6 2710 12 2880
根据表中所给的数据计算第85百分位数.
10.根据所给的以下数据:3.81,3.65,3.68,3.83,3.68,3.80,3.72,3.73,3.75,3.80,求他们的75%,50%分位数.
11.下表记录了一个家庭6月份每天在食品上面的消费金额:(单位:元)
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天 第9天 第10天
31 29 26 32 34 28 34 31 34 34
第11天 第12天 第13天 第14天 第15天 第16天 第17天 第18天 第19天 第20天
35 26 27 35 34 28 28 30 32 28
第21天 第22天 第23天 第24天 第25天 第26天 第27天 第28天 第29天 第30天
32 26 35 34 35 30 28 34 31 29
求该家庭6月份每天在食品上面的消费金额的5%,25%,50%,75%,95%分位数.
12.某校年级长为了解本校高三学生一模考试的数学成绩(单位:分),随机抽取30名学生的一模数学考试,如下所示:
110 144 125 63 89 121 145 123 174 96
97 142 115 68 83 116 139 124 85 98
132 147 128 133 99 117 103 113 96 141
估计该校高三学生一模数学成绩的25%分位数为______,50%分位数为______.
试卷第1页,总3页
【参考答案】
【经典例题】
例1 . 解析: 把 7 人的身高从小到大排列
168,170,172,172,175,176,180
7 × 40% = 2.8
即第 3 个数据为所求的第 40 的百分位数.
答案: C
例2 解析: 把甲、乙两名学生的数学成绩从小到大排序,可得
甲: 65,71,75,76,81,86,88,89,91,94,95,107,110.
乙: 78,79,83,86,88,93,98,98,99,101,103,106,114.
由 13 × 25% = 3.25,13 × 50% = 6.5.
可得数据的 25% 分位数, 50% 分位数为第 4,7 项数据,
即学生甲的 25% 分位数, 50% 分位数分别为 76,88.
学生乙的 25% 分位数, 50% 分位数分别为 86,98.
例3 . 解析: (1) 风景区是这样计算的:
调整前的平均价格为 = 16( 元 ) ,
调整后的平均价格为 = 16( 元 ) ,
∵ 调整前后的平均价格不变,日平均人数不变,
∴ 日平均总收入持平.
(2) 游客是这样计算的:
原日平均总收入为 10 × 1 + 10 × 1 + 15 × 2 + 20 × 3 + 25 × 2 = 160( 千元 ) ,
现日平均总收入为 5 × 1 + 5 × 1 + 15 × 2 + 25 × 3 + 30 × 2 = 175( 千元 ) ,
∴ 调整收费后风景区的日平均总收入增加了 × 100% ≈ 9.4%.
(3) 游客的算法是正确的,游客的说法较能反映整体实际.
【课堂达标】
1.A
【解析】
【分析】
将数据由小到大依次排列,找出第个数,可得出这人成绩的第百分位数.
【详解】
将这人成绩由小到大依次排列为、、、、、、、、、、、、、、,
第个数为,因此,这人成绩的第百分位数是.
故选:A.
【点睛】
本题考查百分位数的计算,熟悉百分位数的定义是计算的关键,考查计算能力,属于基础题.
2.B
【解析】
【分析】
将7人的身高从低到高排列,最后由百分位数的求法求解即可.
【详解】
将7人的身高从低到高排列:
第5个数据为所求的第60百分位数,即这7人的第60百分位数为
故选:B
【点睛】
本题主要考查了求百分位数,属于基础题.
3.C
【解析】
【分析】
先计算分位数的位置,再求出这个数即可.
【详解】
由题意,这10个人的幸福指数已经从小到大排列,
因为,
所以这10个人的分位数是从小到大排列后第8个人的幸福指数,即8.
故选:C
【点睛】
本题主要考查分位数的概念和计算,属于基础题.
4.A
【解析】
【分析】
根据雷达图,对四个选项逐个分析,可选出答案.
【详解】
根据雷达图,可知物理成绩领先年级平均分最多,即A错误;
甲的政治、历史两个科目的成绩低于年级平均分,即B正确;
甲的成绩最好的前两个科目是化学和地理,即C正确;
对甲而言,物理成绩比年级平均分高,历史成绩比年级平均分低,而化学、生物、地理、政治中优势最明显的两科为化学和地理,故物理、化学、地理的成绩是比较理想的一种选科结果,即D正确.
故选:A.
【点睛】
本题考查统计知识,涉及到雷达图的识别及应用,考查学生识图能力、数据分析能力,是一道容易题.
5.B
【解析】
【分析】
由样本数据第80百分位的定义以及求解步骤直接求解即可得出答案.
【详解】
把成绩按从小到大的顺序排列为:
56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,
因为15×80%=12,所以这15人成绩的第80百分位是.
故选:B.
【点睛】
本题考查了样本数据百分位数的计算,属于基础题.
6.36.6
【解析】
【分析】
根据第百分位数的概念和计算方法可得答案.
【详解】
将6名同学某日上午的体温记录从小到大排列为:36.1,36.3, 36.4,36.5,36.6,36.7,
因为,所以该组数据的第80百分位数为36.6,
故答案为:36.6.
【点睛】
本题考查第百分位数的概念和计算方法,属于基础题.
7.33
【解析】
【分析】
该组数据一共有8个,%,再分析75%分位数即可.
【详解】
该组数据一共有8个,%,故75%分位数在从小到大第6,7个数的平均数,
即.
故答案为:33
【点睛】
本题主要考查了分位数的计算,属于基础题型.
【能力提升】
8.(1);(2)平均数为,众数为;(3)分
【解析】
【分析】
(1)根据频率和为,即可求出的值;
(2)根据频率直方图,取频率最大组的中值即为众数;由平均数公式即可求出结论;
(3)先确定从小到大概率和为所在的组,以及在该组所在的比例,即可求出结果.
【详解】
(1)依题意得,,
解得;
(2)估计这名学生历史成绩的平均分为,
,
众数为;
(3)的频率和为,的频率为
所以估计本次入学检测历史学科划定的一本线为.
【点睛】
本题考查补全频率分布直方图,并利用频率直方图求众数、平均数以及估计百分比数,属于基础题.
9.3130
【解析】
【分析】
将所给数据从小到大排列,根据分位数的计算公式可得解.
【详解】
把这组数据按从小到大排序:2710,2755,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325,
所以,
即第85百分位数是3130.
故答案为: 3130
【点睛】
本题考查了百分位数的概念和简单计算,属于基础题.
10.3.80;3.74
【解析】
【分析】
将所给数据从小到大排列,根据分位数的计算公式可得解.
【详解】
把这组数据从小到大排列,得3.65,3.68,3.68,3.72,3.73,3.75,3.80,3.80,3.81,3.83,
,所以75%分位数为3.80,
,则50%分位数为
故答案为: 3.80;3.74
【点睛】
计算一组n个数据的p%分位数的一般步骤如下:第1步,按照从小到大排列原始数据;第2步,计算;第3步,若i不是整数,而大于i的比邻整数为j,则p%分位数为第j项数据;若i是整数,则p%分位数为第i项与第(i+1)项数据的平均数.
11.见解析
【解析】
【分析】
将所有数据由小到大排列,再分别计算总数30的5%,25%,50%,75%,95%再进行对应的分位数计算即可.
【详解】
该样本共有30个数据,所以30×5%=1.5,30×25%=7.5,30×50%=15,30×75%=22.5,
30×95%=28.5
将所有数据由小到大排列得:26,26,26,27,28,28,28,28,28,29,29,30,30,31,3131,32,32,32,34,34,34,34,34,34,34,35,35.
从而得5个百分位数如下表:
百分位数 5% 25% 50% 75% 95%
消费金额/元 26 28 31 34 35
【点睛】
本题主要考查了百分位数的计算,属于基础题型.
12.96. 115.5.
【解析】
【分析】
先将学生的成绩从小到大排列,分别计算25%分位数和50%分位数的位置,再求出这两个数即可.
【详解】
把这30名学生的数学成绩按从小到大的顺序排列为63,68,74,83,85,89,96,96,97,98,99,107,110,113,115,116,117,121,123,124,125,128,132,133,139,141,142,144,145,147.
因为,所以这30名学生一模数学成绩的25%分位数为从小到大排列后第8名学生的成绩,即96,
因为,所以这30名学生一模数学成绩的50%分位数为从小到大排列后第15名同学和第16名同学成绩的平均数,即.
故答案为:96;115.5
【点睛】
本题主要考查分位数的概念和计算,属于基础题.
【教学目标】
重点、难点
重点:样本众数、中位数、平均数的意义及求法,实际问题中三数的应用。
难点:比较复杂的百分数应用题
学科素养
通过对有关数据的收集、整理、分析、判断培养学生“实事求是”的科学态度。
【知识清单】
1 .频率分布表、频率分布直方图的制作步骤及意义
2 .百分位数
(1) 定义:一般地,一组数据的第 p 百分位数是这样一个值,它使得这组数据中至少有 p % 的数据小于或等于这个值,且至少有 (100 - p )% 的数据大于或等于这个值.
(2) 计算步骤:计算一组 n 个数据的第 p 百分位数的步骤:
第 1 步,按 从小到大 排列原始数据.
第 2 步,计算 i = n × p % .
第 3 步,若 i 不是整数,而大于 i 的比邻整数为 j ,则第 p 百分位数为第 j 项数据;若 i 是整数,则第 p 百分位数为第 i 项与第 ( i + 1) 项数据的 平均数 .
【经典例题】
例1. 高二 (1) 班 7 人宿舍中每个同学的身高分别为 170,168,172,172,175,176,180 ,求这 7 人的第 40 的百分位数为 ( )
A . 168 B . 170
C . 172 D . 171
例2 .某中学高二 (2) 班甲、乙两名学生自进入高中以来,每次数学考试成绩情况如下:
甲: 95,81,75,91,86,89,71,65,76,88,94,110,107.
乙: 83,86,93,99,88,103,98,114,98,79,78,106,101.
计算出学生甲、乙的 25% 分位数和 50% 分位数.
例3 . ( 学科素养 — 数据处理 ) 某风景区对 5 个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变.有关数据如表所示:
景点 A B C D E
原价 ( 元 ) 10 10 15 20 25
现价 ( 元 ) 5 5 15 25 30
日平均人数 ( 千人 ) 1 1 2 3 2
(1) 该风景区称调整前后这 5 个景点门票的平均收费不变,日平均总收入持平.问风景区是怎样计算的?
(2) 另一方面,游客认为调整收费后风景区的日平均总收入相对于调价前,实际上增加了约 9.4%. 问游客是怎样计算的?
(3) 你认为风景区和游客哪一个的说法较能反映整体实际?
【课堂达标】
1.以下数据为参加数学竞赛决赛的人的成绩:(单位:分)、、、、、、、、、、、、、、,则这人成绩的第百分位数是( )
A. B. C. D.
2.高二(1)班7人宿舍中每个同学的身高分别为170,168,172,172,175,176,180,求这7人的第60百分位数为( )
A.168 B.175 C.172 D.176
3.“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近表示满意度越高.现随机抽取位北京市民,他们的幸福感指数为3,4,5,5,6,7,7,8,9,10.则这组数据的分位数是( )
A.7 B. C.8 D.
4.2021年起,我市将试行“3+1+2”的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
A.甲的化学成绩领先年级平均分最多.
B.甲有2个科目的成绩低于年级平均分.
C.甲的成绩最好的前两个科目是化学和地理.
D.对甲而言,物理、化学、地理是比较理想的一种选科结果.
5.以下数据为参加数学竞赛决赛的15人的成绩:
78,70,72,86,88,79,80,81,94,84,56,98,83,90,91,
则这15人成绩的第80百分位是( )
A.90 B.90.5 C.91 D.91.5
6.为做好“新冠肺炎”疫情肪控工作,济南市各学校坚持落实“双测温两报告”制度,以下是某宿舍6名同学某日上午的体温记录:36.3,36.1,36.4,36.7,36.5,36.6(单位:),则该组数据的第80百分位数为________.
7.数据:18,26,27,28,30,32,34,40的75%分位数为______.
【能力提升】
8.某学校高三年级在开学时举行了入学检测.为了了解本年级学生寒假期间历史的学习情况,现从年级名文科生中随机抽取了名学生本次考试的历史成绩,得到他们历史分数的频率分布直方图如图.已知本次考试高三年级历史成绩分布区间为.
(1)求图中的值;
(2)根据频率分布直方图,估计这名学生历史成绩的平均分,众数;(每组数据用该组的区间中点值作代表)
(3)已知该学校每年高考有%的同学历史成绩在一本线以上,用样本估计总体的方法,请你估计本次入学检测历史学科划定的一本线该为多少分?
9.下表为12位毕业生的起始月薪
毕业生 起始月薪 毕业生 起始月薪
1 2850 7 2890
2 2950 8 3130
3 3050 9 2940
4 2880 10 3325
5 2755 11 2920
6 2710 12 2880
根据表中所给的数据计算第85百分位数.
10.根据所给的以下数据:3.81,3.65,3.68,3.83,3.68,3.80,3.72,3.73,3.75,3.80,求他们的75%,50%分位数.
11.下表记录了一个家庭6月份每天在食品上面的消费金额:(单位:元)
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天 第9天 第10天
31 29 26 32 34 28 34 31 34 34
第11天 第12天 第13天 第14天 第15天 第16天 第17天 第18天 第19天 第20天
35 26 27 35 34 28 28 30 32 28
第21天 第22天 第23天 第24天 第25天 第26天 第27天 第28天 第29天 第30天
32 26 35 34 35 30 28 34 31 29
求该家庭6月份每天在食品上面的消费金额的5%,25%,50%,75%,95%分位数.
12.某校年级长为了解本校高三学生一模考试的数学成绩(单位:分),随机抽取30名学生的一模数学考试,如下所示:
110 144 125 63 89 121 145 123 174 96
97 142 115 68 83 116 139 124 85 98
132 147 128 133 99 117 103 113 96 141
估计该校高三学生一模数学成绩的25%分位数为______,50%分位数为______.
试卷第1页,总3页
【参考答案】
【经典例题】
例1 . 解析: 把 7 人的身高从小到大排列
168,170,172,172,175,176,180
7 × 40% = 2.8
即第 3 个数据为所求的第 40 的百分位数.
答案: C
例2 解析: 把甲、乙两名学生的数学成绩从小到大排序,可得
甲: 65,71,75,76,81,86,88,89,91,94,95,107,110.
乙: 78,79,83,86,88,93,98,98,99,101,103,106,114.
由 13 × 25% = 3.25,13 × 50% = 6.5.
可得数据的 25% 分位数, 50% 分位数为第 4,7 项数据,
即学生甲的 25% 分位数, 50% 分位数分别为 76,88.
学生乙的 25% 分位数, 50% 分位数分别为 86,98.
例3 . 解析: (1) 风景区是这样计算的:
调整前的平均价格为 = 16( 元 ) ,
调整后的平均价格为 = 16( 元 ) ,
∵ 调整前后的平均价格不变,日平均人数不变,
∴ 日平均总收入持平.
(2) 游客是这样计算的:
原日平均总收入为 10 × 1 + 10 × 1 + 15 × 2 + 20 × 3 + 25 × 2 = 160( 千元 ) ,
现日平均总收入为 5 × 1 + 5 × 1 + 15 × 2 + 25 × 3 + 30 × 2 = 175( 千元 ) ,
∴ 调整收费后风景区的日平均总收入增加了 × 100% ≈ 9.4%.
(3) 游客的算法是正确的,游客的说法较能反映整体实际.
【课堂达标】
1.A
【解析】
【分析】
将数据由小到大依次排列,找出第个数,可得出这人成绩的第百分位数.
【详解】
将这人成绩由小到大依次排列为、、、、、、、、、、、、、、,
第个数为,因此,这人成绩的第百分位数是.
故选:A.
【点睛】
本题考查百分位数的计算,熟悉百分位数的定义是计算的关键,考查计算能力,属于基础题.
2.B
【解析】
【分析】
将7人的身高从低到高排列,最后由百分位数的求法求解即可.
【详解】
将7人的身高从低到高排列:
第5个数据为所求的第60百分位数,即这7人的第60百分位数为
故选:B
【点睛】
本题主要考查了求百分位数,属于基础题.
3.C
【解析】
【分析】
先计算分位数的位置,再求出这个数即可.
【详解】
由题意,这10个人的幸福指数已经从小到大排列,
因为,
所以这10个人的分位数是从小到大排列后第8个人的幸福指数,即8.
故选:C
【点睛】
本题主要考查分位数的概念和计算,属于基础题.
4.A
【解析】
【分析】
根据雷达图,对四个选项逐个分析,可选出答案.
【详解】
根据雷达图,可知物理成绩领先年级平均分最多,即A错误;
甲的政治、历史两个科目的成绩低于年级平均分,即B正确;
甲的成绩最好的前两个科目是化学和地理,即C正确;
对甲而言,物理成绩比年级平均分高,历史成绩比年级平均分低,而化学、生物、地理、政治中优势最明显的两科为化学和地理,故物理、化学、地理的成绩是比较理想的一种选科结果,即D正确.
故选:A.
【点睛】
本题考查统计知识,涉及到雷达图的识别及应用,考查学生识图能力、数据分析能力,是一道容易题.
5.B
【解析】
【分析】
由样本数据第80百分位的定义以及求解步骤直接求解即可得出答案.
【详解】
把成绩按从小到大的顺序排列为:
56,70,72,78,79,80,81,83,84,86,88,90,91,94,98,
因为15×80%=12,所以这15人成绩的第80百分位是.
故选:B.
【点睛】
本题考查了样本数据百分位数的计算,属于基础题.
6.36.6
【解析】
【分析】
根据第百分位数的概念和计算方法可得答案.
【详解】
将6名同学某日上午的体温记录从小到大排列为:36.1,36.3, 36.4,36.5,36.6,36.7,
因为,所以该组数据的第80百分位数为36.6,
故答案为:36.6.
【点睛】
本题考查第百分位数的概念和计算方法,属于基础题.
7.33
【解析】
【分析】
该组数据一共有8个,%,再分析75%分位数即可.
【详解】
该组数据一共有8个,%,故75%分位数在从小到大第6,7个数的平均数,
即.
故答案为:33
【点睛】
本题主要考查了分位数的计算,属于基础题型.
【能力提升】
8.(1);(2)平均数为,众数为;(3)分
【解析】
【分析】
(1)根据频率和为,即可求出的值;
(2)根据频率直方图,取频率最大组的中值即为众数;由平均数公式即可求出结论;
(3)先确定从小到大概率和为所在的组,以及在该组所在的比例,即可求出结果.
【详解】
(1)依题意得,,
解得;
(2)估计这名学生历史成绩的平均分为,
,
众数为;
(3)的频率和为,的频率为
所以估计本次入学检测历史学科划定的一本线为.
【点睛】
本题考查补全频率分布直方图,并利用频率直方图求众数、平均数以及估计百分比数,属于基础题.
9.3130
【解析】
【分析】
将所给数据从小到大排列,根据分位数的计算公式可得解.
【详解】
把这组数据按从小到大排序:2710,2755,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325,
所以,
即第85百分位数是3130.
故答案为: 3130
【点睛】
本题考查了百分位数的概念和简单计算,属于基础题.
10.3.80;3.74
【解析】
【分析】
将所给数据从小到大排列,根据分位数的计算公式可得解.
【详解】
把这组数据从小到大排列,得3.65,3.68,3.68,3.72,3.73,3.75,3.80,3.80,3.81,3.83,
,所以75%分位数为3.80,
,则50%分位数为
故答案为: 3.80;3.74
【点睛】
计算一组n个数据的p%分位数的一般步骤如下:第1步,按照从小到大排列原始数据;第2步,计算;第3步,若i不是整数,而大于i的比邻整数为j,则p%分位数为第j项数据;若i是整数,则p%分位数为第i项与第(i+1)项数据的平均数.
11.见解析
【解析】
【分析】
将所有数据由小到大排列,再分别计算总数30的5%,25%,50%,75%,95%再进行对应的分位数计算即可.
【详解】
该样本共有30个数据,所以30×5%=1.5,30×25%=7.5,30×50%=15,30×75%=22.5,
30×95%=28.5
将所有数据由小到大排列得:26,26,26,27,28,28,28,28,28,29,29,30,30,31,3131,32,32,32,34,34,34,34,34,34,34,35,35.
从而得5个百分位数如下表:
百分位数 5% 25% 50% 75% 95%
消费金额/元 26 28 31 34 35
【点睛】
本题主要考查了百分位数的计算,属于基础题型.
12.96. 115.5.
【解析】
【分析】
先将学生的成绩从小到大排列,分别计算25%分位数和50%分位数的位置,再求出这两个数即可.
【详解】
把这30名学生的数学成绩按从小到大的顺序排列为63,68,74,83,85,89,96,96,97,98,99,107,110,113,115,116,117,121,123,124,125,128,132,133,139,141,142,144,145,147.
因为,所以这30名学生一模数学成绩的25%分位数为从小到大排列后第8名学生的成绩,即96,
因为,所以这30名学生一模数学成绩的50%分位数为从小到大排列后第15名同学和第16名同学成绩的平均数,即.
故答案为:96;115.5
【点睛】
本题主要考查分位数的概念和计算,属于基础题.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
