2022—2023学年人教版数学八年级上册11.3.2多边形的内角和 课件(共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册11.3.2多边形的内角和 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 687.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 17:45:39 | ||
图片预览

文档简介
(共15张PPT)
11.3.2多边形的内角和
问题2 你知道长方形和正方形的内角和是多少 度?
问题1 三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
问题3 猜想任意四边形的内角和是多少度?
讲授新课
多边形的内角和
一
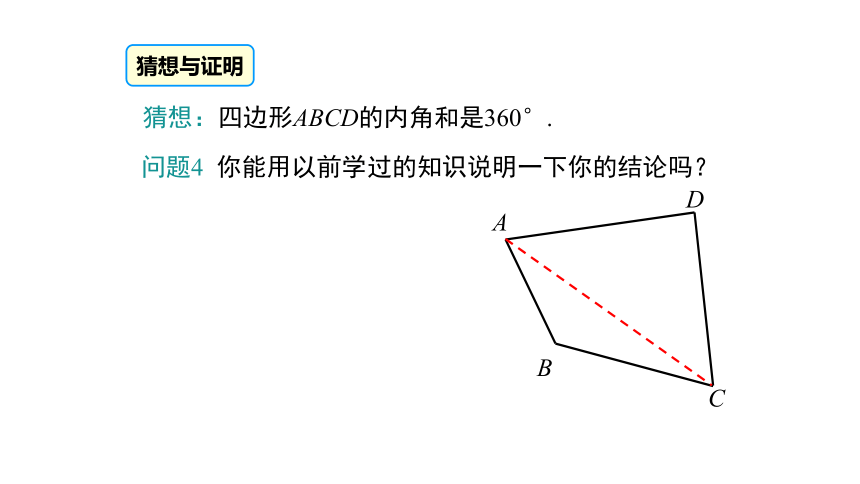
猜想:四边形ABCD的内角和是360°.
问题4 你能用以前学过的知识说明一下你的结论吗?
猜想与证明
A
B
C
D
A
C
D
B
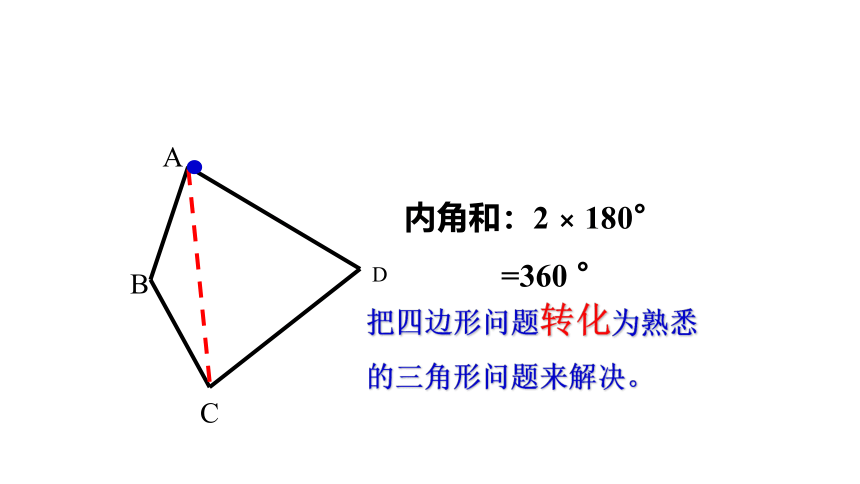
内角和:2 × 180°
=360 °
把四边形问题转化为熟悉
的三角形问题来解决。
.
A
C
D
B
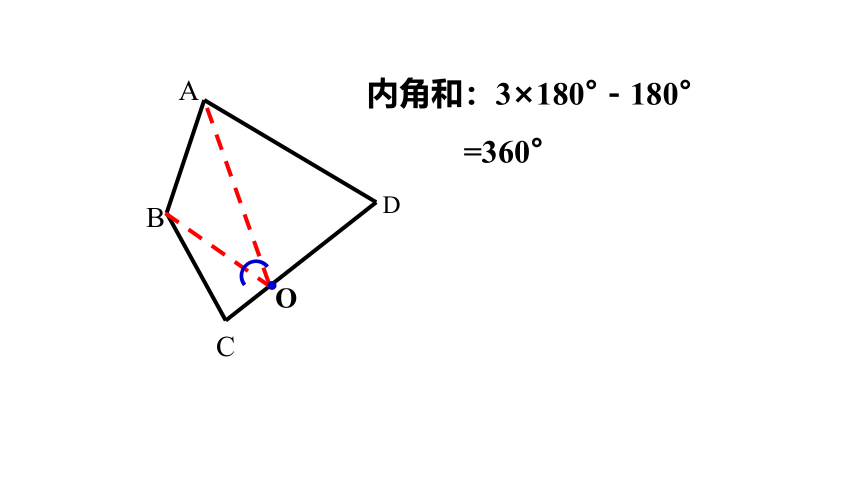
内角和:3×180°-180°
=360°
.
O
⌒
A
C
D
B
O
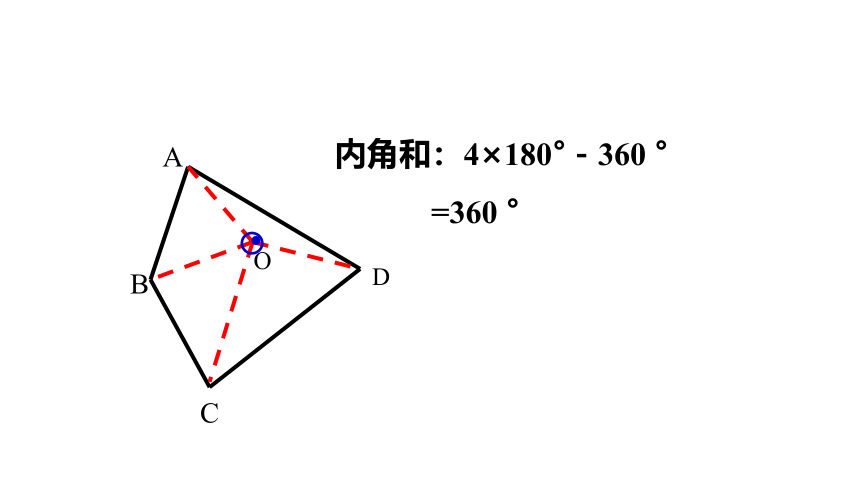
内角和:4×180°-360 °
=360 °
.
A
C
D
B
A
C
D
B
O
.
C
A
D
B
.
O
⌒
A
C
D
B
O
.
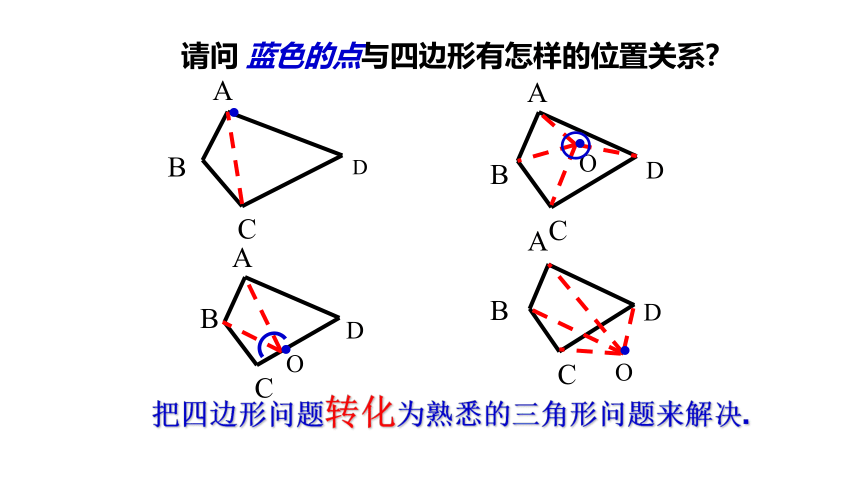
把四边形问题转化为熟悉的三角形问题来解决.
.
请问 蓝色的点与四边形有怎样的位置关系?
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
如图,已知四边形ABCD中,∠A+∠C=180°,求∠B与∠D的关系.
分析:∠A、∠B、∠C、∠D有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°=360°
又∠A+∠C=180°
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说,如果四边形一组对角互补,那么另一组对角也互补.
我们能不能利用刚才的方法分割五边形,六边形,n边形呢?
分割是种方法,找到规律为途径,归纳多边形内角和定理才是目标。
分组讨论,利用黑板充分展示。
探索
温馨提示
A
B
C
E
D
5×180°-360°=540°
五边形还可以这样分:
A
B
C
D
E
F
六边形还可以这样分:
6×180 -360°=720
4
5
6
7
…
n
多边形的内角和
分成的三角形的个数
多边形的边数
4
5
6
7
…
n
…
180 °×n-360°
180°×7-360°
180°×6-360°
180 °
×5 -360°
180 °
×4 -360°
课堂练习难点巩固求出图中X的值(1)X=65°(2)X=60°思考题
如果一个四边形四个内角之比是2∶2∶3∶5,那么这个四边形的四个内角中
(A)只有一个直角 (B)只有一个锐角
(C)有两个直角 (D)有两个钝角
若一个角的两边与另一个角的两边互相垂直,且这两个角的差为46°,那么这两个角的度数分别为_________.
A
113 °,57 °
【课堂小结】
小结
(1)将求多边形内角和转化求三角形的内角和,化未知为已知。
(2)n边形的内角和等于(n-2)×180°,
多边形的内角和是180°的整数倍
多边形的边数增加1,内角和增加180
从特殊到一般
11.3.2多边形的内角和
问题2 你知道长方形和正方形的内角和是多少 度?
问题1 三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
问题3 猜想任意四边形的内角和是多少度?
讲授新课
多边形的内角和
一
猜想:四边形ABCD的内角和是360°.
问题4 你能用以前学过的知识说明一下你的结论吗?
猜想与证明
A
B
C
D
A
C
D
B
内角和:2 × 180°
=360 °
把四边形问题转化为熟悉
的三角形问题来解决。
.
A
C
D
B
内角和:3×180°-180°
=360°
.
O
⌒
A
C
D
B
O
内角和:4×180°-360 °
=360 °
.
A
C
D
B
A
C
D
B
O
.
C
A
D
B
.
O
⌒
A
C
D
B
O
.
把四边形问题转化为熟悉的三角形问题来解决.
.
请问 蓝色的点与四边形有怎样的位置关系?
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
如图,已知四边形ABCD中,∠A+∠C=180°,求∠B与∠D的关系.
分析:∠A、∠B、∠C、∠D有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°=360°
又∠A+∠C=180°
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说,如果四边形一组对角互补,那么另一组对角也互补.
我们能不能利用刚才的方法分割五边形,六边形,n边形呢?
分割是种方法,找到规律为途径,归纳多边形内角和定理才是目标。
分组讨论,利用黑板充分展示。
探索
温馨提示
A
B
C
E
D
5×180°-360°=540°
五边形还可以这样分:
A
B
C
D
E
F
六边形还可以这样分:
6×180 -360°=720
4
5
6
7
…
n
多边形的内角和
分成的三角形的个数
多边形的边数
4
5
6
7
…
n
…
180 °×n-360°
180°×7-360°
180°×6-360°
180 °
×5 -360°
180 °
×4 -360°
课堂练习难点巩固求出图中X的值(1)X=65°(2)X=60°思考题
如果一个四边形四个内角之比是2∶2∶3∶5,那么这个四边形的四个内角中
(A)只有一个直角 (B)只有一个锐角
(C)有两个直角 (D)有两个钝角
若一个角的两边与另一个角的两边互相垂直,且这两个角的差为46°,那么这两个角的度数分别为_________.
A
113 °,57 °
【课堂小结】
小结
(1)将求多边形内角和转化求三角形的内角和,化未知为已知。
(2)n边形的内角和等于(n-2)×180°,
多边形的内角和是180°的整数倍
多边形的边数增加1,内角和增加180
从特殊到一般
