2022-2023学年人教版八年级数学上册12.2.2 三角形全等的判定SAS 课件 (共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2.2 三角形全等的判定SAS 课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1005.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 18:03:24 | ||
图片预览



文档简介
(共15张PPT)
12.2.2 三角形全等的判定SAS
任务一:旧知回顾
1、全等三角形的概念
2、全等三角形的性质
3、上节课我们学习了判定两个三角形全等的哪种方法?
(这些内容你还都记得吗?)
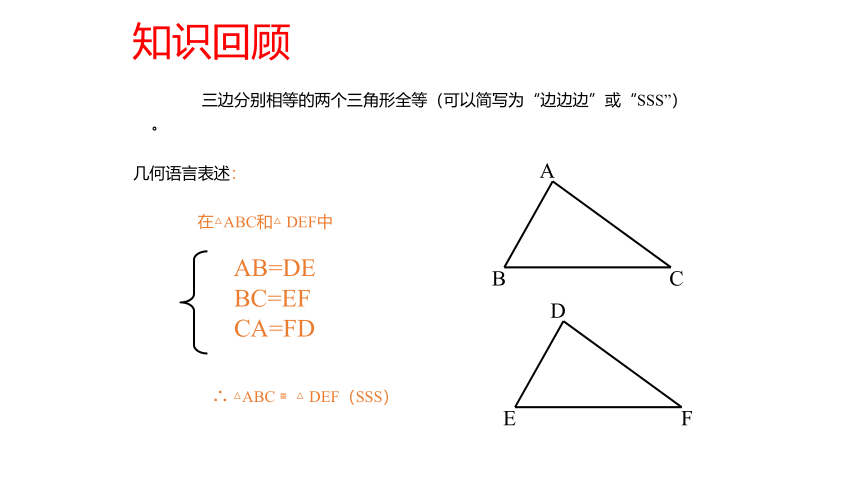
知识回顾
三边分别相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
几何语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
A
B
C
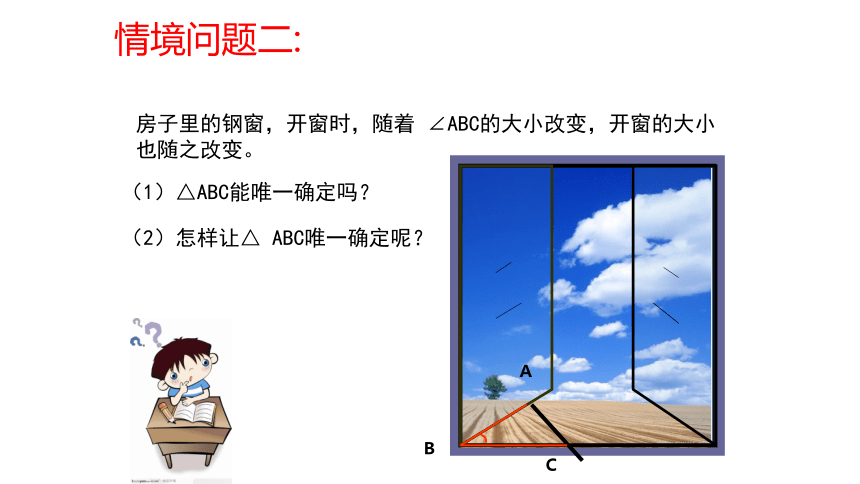
(2)怎样让△ ABC唯一确定呢?
(1)△ABC能唯一确定吗?
房子里的钢窗,开窗时,随着 ∠ABC的大小改变,开窗的大小也随之改变。
情境问题二:
想一想:
三角形有六个基本元素(三边三角),要确定
一个三角形的形状,需要几个元素呢?
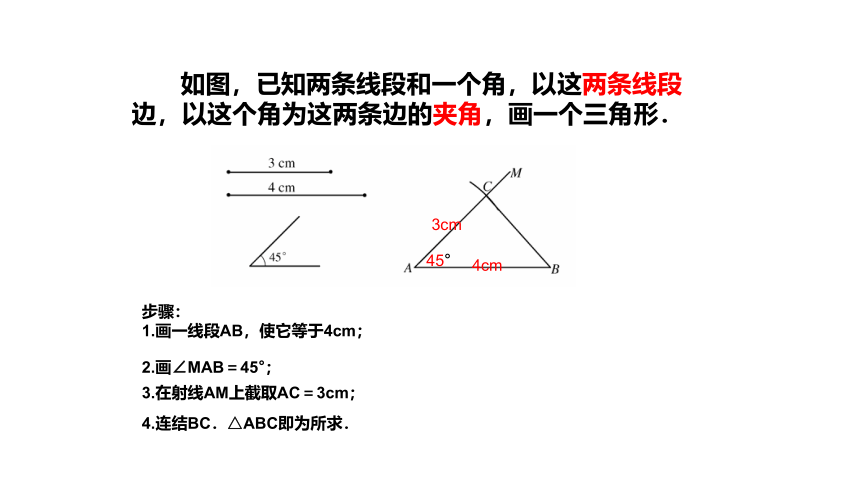
如图,已知两条线段和一个角,以这两条线段
边,以这个角为这两条边的夹角,画一个三角形.
步骤:
1.画一线段AB,使它等于4cm;
4cm
45°
3cm
2.画∠MAB=45°;
3.在射线AM上截取AC=3cm;
4.连结BC.△ABC即为所求.
A
B
C
D
E
F
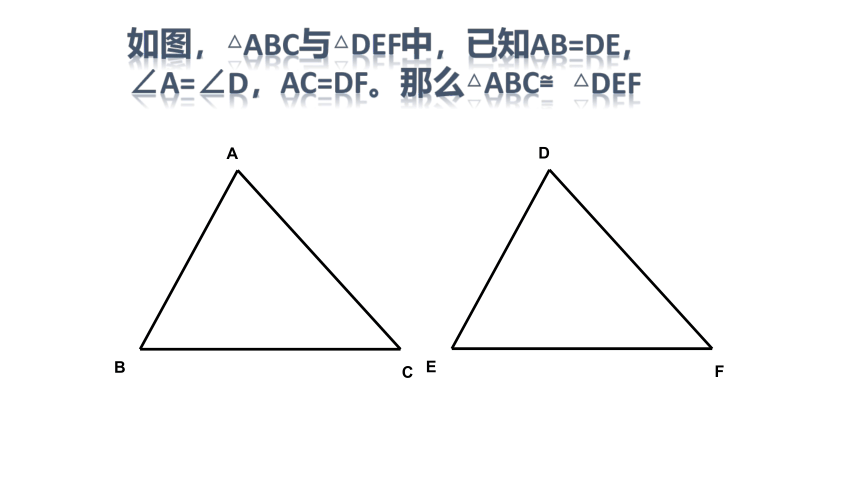
如图,△abc与△def中,已知ab=de,∠a=∠d,ac=df。那么△abc≌△def
判定两个三角形全等的第一种方法就是下面
的基本事实:
\\
\
A
B
C
\\
\
D
E
F
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”(S表示边,A表示角)
定理小结:
例1
A
B
C
D
E
1
2
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接AC并延长到点D,使CD =CA,连接BC 并延长到点E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?
证明:在△ABC 和△DEC 中,
D
E
AC = DC(已知),
∠1 =∠2 (对顶角相等),
BC =EC(已知) ,
∴ △ABC ≌△DEC(SAS).
∴ AB =DE
(全等三角形的对应边相等).
A
B
C
D
E
1
2
练一练
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA 根据“SAS”
AD=CB
B
C
D
E
E
A
A
D
例2:如图,已知AB=AC,AD=AE。
求证:∠B=∠C
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
范例学习
A
C
B
练习1:已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
边:
角:
边:
AB=CB(已知)
∠ABD= ∠CBD(已知)
?
A
B
D
(SAS)
2: 已知:点A、E、F、C在同一条直线上, AD=CB,AD∥CB,AE=CF. 求证:EB∥DF
AF=CE (已证)
∠A=∠C (已证)
AD=CB (已知)
∴△AFD ≌ △CEB(SAS)
∴ ∠AFD=∠CEB
∴ EB∥DF
(两直线平行,内错角相等)
∵ AE=CF (已知)
∴ AE+EF=CF+EF
(等式的性质)
即 AF=CE
证明:
∵ AD∥CB(已知)
∴ ∠A=∠C
在△AFD与△CEB中
A
D
C
E
F
B
∵
课堂小结:
2. 用尺规作图:已知两边及其夹角的三角形画三角形
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
3、会判定三角形全等
12.2.2 三角形全等的判定SAS
任务一:旧知回顾
1、全等三角形的概念
2、全等三角形的性质
3、上节课我们学习了判定两个三角形全等的哪种方法?
(这些内容你还都记得吗?)
知识回顾
三边分别相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
几何语言表述:
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
A
B
C
(2)怎样让△ ABC唯一确定呢?
(1)△ABC能唯一确定吗?
房子里的钢窗,开窗时,随着 ∠ABC的大小改变,开窗的大小也随之改变。
情境问题二:
想一想:
三角形有六个基本元素(三边三角),要确定
一个三角形的形状,需要几个元素呢?
如图,已知两条线段和一个角,以这两条线段
边,以这个角为这两条边的夹角,画一个三角形.
步骤:
1.画一线段AB,使它等于4cm;
4cm
45°
3cm
2.画∠MAB=45°;
3.在射线AM上截取AC=3cm;
4.连结BC.△ABC即为所求.
A
B
C
D
E
F
如图,△abc与△def中,已知ab=de,∠a=∠d,ac=df。那么△abc≌△def
判定两个三角形全等的第一种方法就是下面
的基本事实:
\\
\
A
B
C
\\
\
D
E
F
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”(S表示边,A表示角)
定理小结:
例1
A
B
C
D
E
1
2
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和B. 连接AC并延长到点D,使CD =CA,连接BC 并延长到点E,使CE =CB,连接ED,那么量出DE的长就是A,B的距离.为什么?
证明:在△ABC 和△DEC 中,
D
E
AC = DC(已知),
∠1 =∠2 (对顶角相等),
BC =EC(已知) ,
∴ △ABC ≌△DEC(SAS).
∴ AB =DE
(全等三角形的对应边相等).
A
B
C
D
E
1
2
练一练
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD 根据“SAS”
△ADC≌△CBA 根据“SAS”
AD=CB
B
C
D
E
E
A
A
D
例2:如图,已知AB=AC,AD=AE。
求证:∠B=∠C
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形对应角相等)
范例学习
A
C
B
练习1:已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
边:
角:
边:
AB=CB(已知)
∠ABD= ∠CBD(已知)
?
A
B
D
(SAS)
2: 已知:点A、E、F、C在同一条直线上, AD=CB,AD∥CB,AE=CF. 求证:EB∥DF
AF=CE (已证)
∠A=∠C (已证)
AD=CB (已知)
∴△AFD ≌ △CEB(SAS)
∴ ∠AFD=∠CEB
∴ EB∥DF
(两直线平行,内错角相等)
∵ AE=CF (已知)
∴ AE+EF=CF+EF
(等式的性质)
即 AF=CE
证明:
∵ AD∥CB(已知)
∴ ∠A=∠C
在△AFD与△CEB中
A
D
C
E
F
B
∵
课堂小结:
2. 用尺规作图:已知两边及其夹角的三角形画三角形
1. 三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等 (边角边或SAS)
3、会判定三角形全等
