2022-2023学年人教版八年级数学上册12.3 角的平分线的性质 课件(共15张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.3 角的平分线的性质 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 649.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 17:49:07 | ||
图片预览




文档简介
(共15张PPT)
12.3 角的平分线的性质
知识储备
活动1 我现在出示一个∠AOB,请同学们找到它的角平分线OC,并画出来.
三角尺的任意一个角平分线怎么找?
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
活动2
我现在拿出一个工具,其中AB=AD,BC=DC.它可以帮我们找到任意角的角平分线,聪明的你知道其中的道理吗?
你觉得这个工具是什么原理?
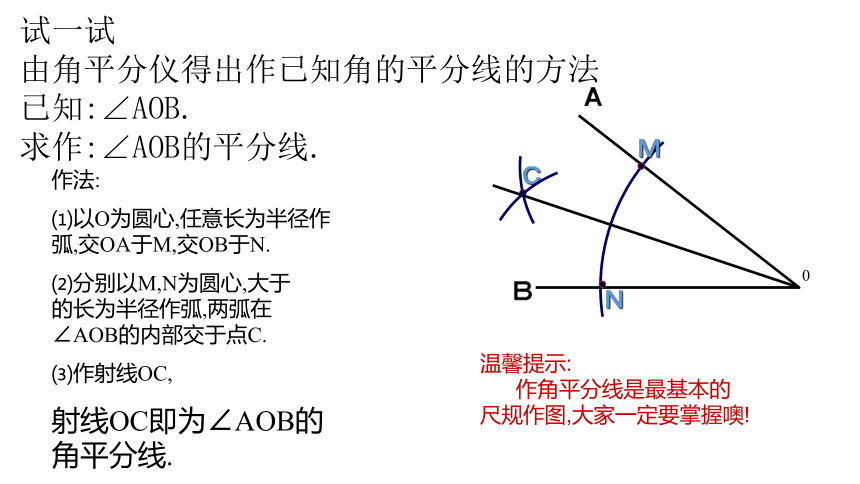
试一试
由角平分仪得出作已知角的平分线的方法
已知:∠AOB.
求作:∠AOB的平分线.
作法:
⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,
射线OC即为∠AOB的角平分线.
B
M
N
C
0
A
温馨提示:
作角平分线是最基本的尺规作图,大家一定要掌握噢!
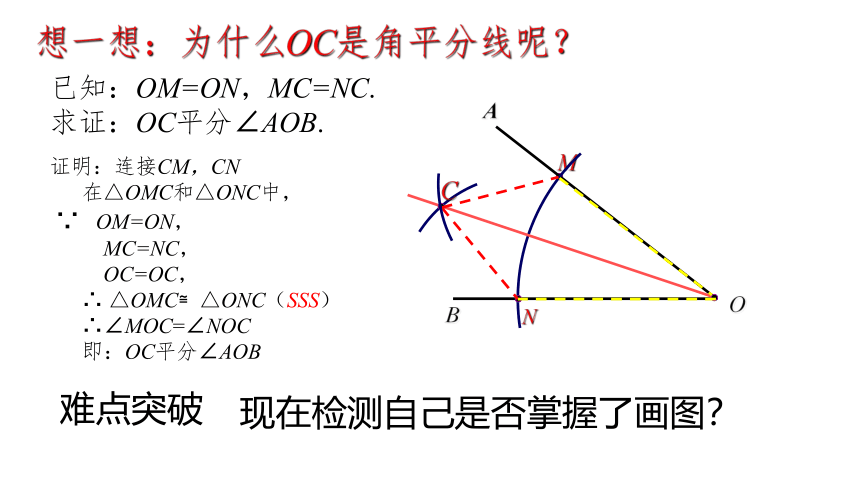
想一想:为什么OC是角平分线呢?
已知:OM=ON,MC=NC.
求证:OC平分∠AOB.
证明:连接CM,CN
在△OMC和△ONC中,
∵ OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
现在检测自己是否掌握了画图?
难点突破
A
M
B
N
C
O
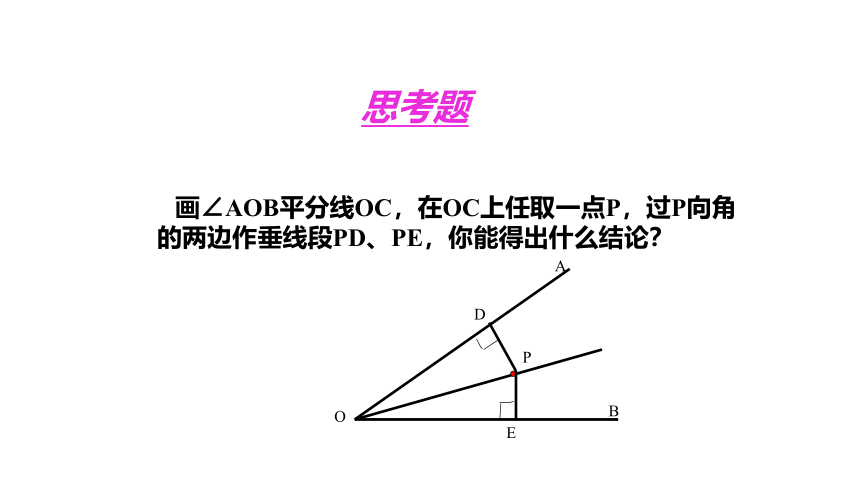
画∠AOB平分线OC,在OC上任取一点P,过P向角的两边作垂线段PD、PE,你能得出什么结论?
思考题
A
O
B
P
E
D
A
O
B
E
D
P
C
你能用三角形全等证明PD=PE吗?
探究性质
在∠AOB的平分线OC上任取一点P ,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE的长度,它们相等吗?
猜想:角的平分线上的点到角的两边的距离相等。
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E。
求证: PD=PE。
A
O
B
E
D
P
C
1
2
证明:
在△ ODP和△OEP中
∠ODP=∠OEP
∠1 = ∠2
OP=OP
∵PD⊥OA,PE⊥OB
∴∠ODP=∠OEP=90o
∵ OC平分∠AOB
∴∠1= ∠2
∴△ODP≌△OEP (AAS)
∴PD=PE
到一个角的两边的距离相等的点,在这个角平分线上。
已知:PD ⊥OA ,PE ⊥OB,垂足分别是D、E,
PD=PE. 求证: 点P在∠AOB的平分线上。
角平分线的判定
A
O
B
P
D
E
C
定理:
用符号语言表示为:
∵PD=PE
PD ⊥OA ,PE ⊥OB
∴ ∠1= ∠2 .
到一个角的两边的距离相等的点,在这个角平分线上。
已知:PD ⊥OA ,PE ⊥OB,垂足分别是D、E,
PD=PE. 求证: 点P在∠AOB的平分线上。
角平分线的判定
A
O
B
P
D
E
C
定理:
用符号语言表示为:
∵PD=PE
PD ⊥OA ,PE ⊥OB
∴ ∠1= ∠2 .
由上面两个定理可知:到角的两边的距离相等的点,都在这个角平分线上;反过来,角平分线上的点到角的两边的距离相等。
角的平分线是到角的两边距离相等的所有点的集合.
练一练
填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到一个角的两边的距离相等的点,在这个角平分线上。
在角平分线上的点到角的两边的距离相等
已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
巩固练习
在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BC=7,DE=3.
求BD的长。
E
D
C
B
A
提升练习
BD=4
课堂小结
2.角的平分线的性质定理:
1.尺规作已知角的平分线。(角平分仪器)
(注意作图痕迹和几何语言的表达)
角的平分线上的点到角的两边的距离相等。
3:角平分线的性质的应用
12.3 角的平分线的性质
知识储备
活动1 我现在出示一个∠AOB,请同学们找到它的角平分线OC,并画出来.
三角尺的任意一个角平分线怎么找?
活动与探究(温馨提示:规范操作、注意安全)
知识讲解
活动2
我现在拿出一个工具,其中AB=AD,BC=DC.它可以帮我们找到任意角的角平分线,聪明的你知道其中的道理吗?
你觉得这个工具是什么原理?
试一试
由角平分仪得出作已知角的平分线的方法
已知:∠AOB.
求作:∠AOB的平分线.
作法:
⑴以O为圆心,任意长为半径作弧,交OA于M,交OB于N.
⑵分别以M,N为圆心,大于 的长为半径作弧,两弧在∠AOB的内部交于点C.
⑶作射线OC,
射线OC即为∠AOB的角平分线.
B
M
N
C
0
A
温馨提示:
作角平分线是最基本的尺规作图,大家一定要掌握噢!
想一想:为什么OC是角平分线呢?
已知:OM=ON,MC=NC.
求证:OC平分∠AOB.
证明:连接CM,CN
在△OMC和△ONC中,
∵ OM=ON,
MC=NC,
OC=OC,
∴ △OMC≌△ONC(SSS)
∴∠MOC=∠NOC
即:OC平分∠AOB
现在检测自己是否掌握了画图?
难点突破
A
M
B
N
C
O
画∠AOB平分线OC,在OC上任取一点P,过P向角的两边作垂线段PD、PE,你能得出什么结论?
思考题
A
O
B
P
E
D
A
O
B
E
D
P
C
你能用三角形全等证明PD=PE吗?
探究性质
在∠AOB的平分线OC上任取一点P ,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE的长度,它们相等吗?
猜想:角的平分线上的点到角的两边的距离相等。
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E。
求证: PD=PE。
A
O
B
E
D
P
C
1
2
证明:
在△ ODP和△OEP中
∠ODP=∠OEP
∠1 = ∠2
OP=OP
∵PD⊥OA,PE⊥OB
∴∠ODP=∠OEP=90o
∵ OC平分∠AOB
∴∠1= ∠2
∴△ODP≌△OEP (AAS)
∴PD=PE
到一个角的两边的距离相等的点,在这个角平分线上。
已知:PD ⊥OA ,PE ⊥OB,垂足分别是D、E,
PD=PE. 求证: 点P在∠AOB的平分线上。
角平分线的判定
A
O
B
P
D
E
C
定理:
用符号语言表示为:
∵PD=PE
PD ⊥OA ,PE ⊥OB
∴ ∠1= ∠2 .
到一个角的两边的距离相等的点,在这个角平分线上。
已知:PD ⊥OA ,PE ⊥OB,垂足分别是D、E,
PD=PE. 求证: 点P在∠AOB的平分线上。
角平分线的判定
A
O
B
P
D
E
C
定理:
用符号语言表示为:
∵PD=PE
PD ⊥OA ,PE ⊥OB
∴ ∠1= ∠2 .
由上面两个定理可知:到角的两边的距离相等的点,都在这个角平分线上;反过来,角平分线上的点到角的两边的距离相等。
角的平分线是到角的两边距离相等的所有点的集合.
练一练
填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(1). ∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
A
C
D
E
B
1
2
∠1= ∠2
DC=DE
到一个角的两边的距离相等的点,在这个角平分线上。
在角平分线上的点到角的两边的距离相等
已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
B
A
E
D
C
F
巩固练习
在△ABC中, ∠ C=90 ° ,AD为∠BAC的平分线,DE⊥AB,BC=7,DE=3.
求BD的长。
E
D
C
B
A
提升练习
BD=4
课堂小结
2.角的平分线的性质定理:
1.尺规作已知角的平分线。(角平分仪器)
(注意作图痕迹和几何语言的表达)
角的平分线上的点到角的两边的距离相等。
3:角平分线的性质的应用
