2022-2023学年人教版九年级数学上册22.1.4二次函数y=ax2+ bx+ c的图象和性质课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册22.1.4二次函数y=ax2+ bx+ c的图象和性质课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 18:58:58 | ||
图片预览






文档简介
(共20张PPT)
22.1 二次函数的图象和性质
1.4二次函数
的图象和性质(2)
学习目标
1.经历对用待定系数法求二次函数解析式的探究,掌握待定系数法求解析式的方法;
2.能灵活地根据条件恰当选取解析式,体会二次函数解析式之间的转化;
3.经历探究过程,培养学生数学运算的核心素养,并养成良好的运算习惯;
4.在学习过程中,感受学习数学知识的价值,提高对数学学习的兴趣.
重点
二次函数的图象性质
难点
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
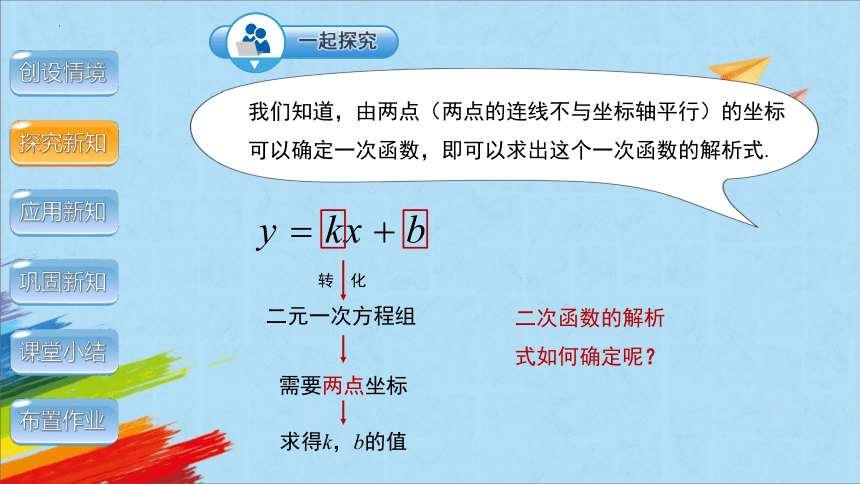
我们知道,由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式.
一起探究
二次函数的解析式如何确定呢?
转 化
求得k,b的值
二元一次方程组
需要两点坐标
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
二次函数 的解析式中有几个待定系数?
3个待定系数
需要图象上的几个点?
3个点
转化成什么样的方程组?
三元一次方程组
创设情境
巩固新知
课堂小结
布置作业
设所求二次函数为 .
解:
二次函数 经过( ,10),(1,4),(2,7)三点,请求出这个二次函数的解析式.
例1:
由已知,函数图象经过( ,10),(1,4),(2,7)三点,得关于a,b,c的三元一次方程组
二次函数解析式为 .
探究新知
应用新知
典型例题
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
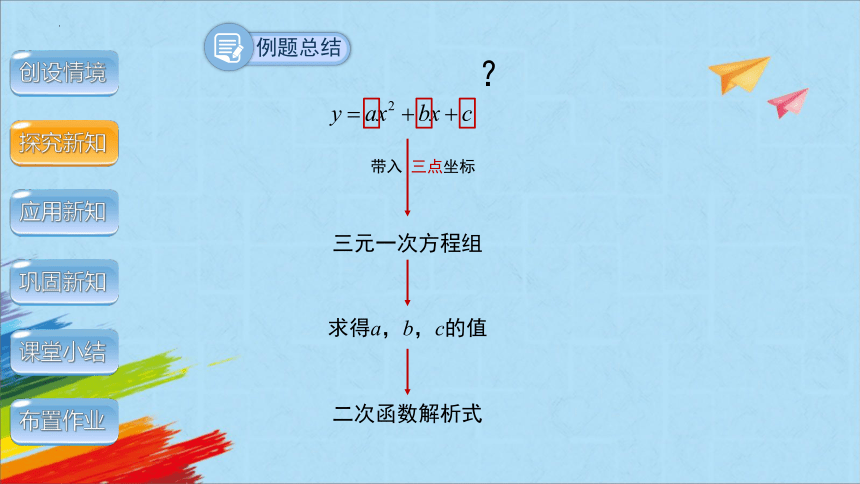
?
二次函数解析式
带入 三点坐标
三元一次方程组
求得a,b,c的值
例题总结
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
由已知,函数图象顶点坐标(1, ),且过B(2,1) 点,得关于a,h,k的方程
设所求二次函数为 .
应用新知
典型例题
二次函数解析式为 .
如果知道二次函数的顶点坐标为A(1, ),且过B(2,1) 点,请求出解析式.
例2:
创设情境
巩固新知
课堂小结
布置作业
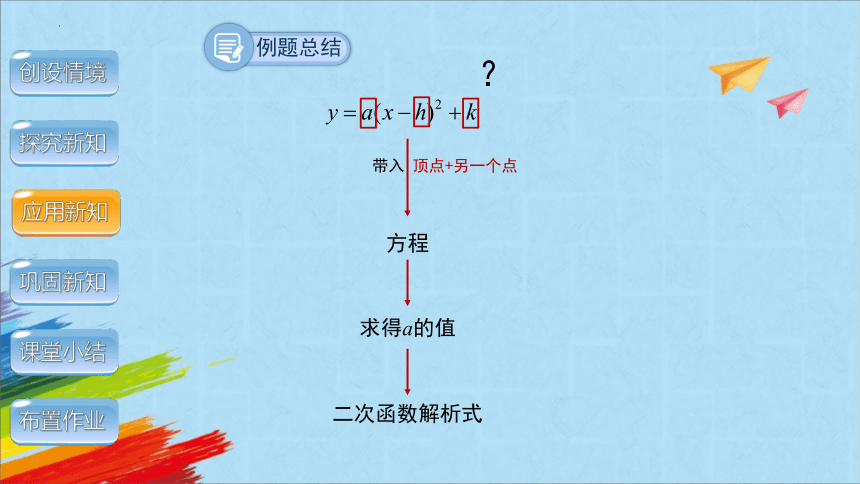
二次函数解析式
带入 顶点+另一个点
方程
求得a的值
?
探究新知
应用新知
例题总结
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
如果知道二次函数的顶点坐标为A(1, ),且过B(2,1) 点,请求出解析式.
二次函数解析式为 .
应用新知
典型例题
例2:
设所求二次函数为 .
由已知,函数图象顶点坐标(1, ),且过B(2,1) 点,得
解法二
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
应用新知
典型例题
例3:
设所求二次函数为 .
解法一
二次函数解析式为 .
一个二次函数,当自变量 时,函数值 ,当 与 时, .求二次函数的解析式.
由已知,函数图象经过( 0 , ),( ,0),( ,0)得到关于 的三元一次方程组:
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
应用新知
典型例题
又∵抛物线过点(0, ),
解法二
设所求二次函数为 ,其中 .
由抛物线过点( , 0 ),( ,0)可知 , ;
∴解析式为 ;
∴ ,即 ;
二次函数为 .
例3:
一个二次函数,当自变量 时,函数值 ,当 与 时, .求二次函数的解析式.
便捷
创设情境
巩固新知
课堂小结
布置作业
二次函数解析式
带入 与x轴两交点+另一个点
方程
求得a的值
?
探究新知
应用新知
例题总结
创设情境
巩固新知
课堂小结
布置作业
探究新知
应用新知
例题总结
顶点式
两点式
一般式
若无特殊点,设一般式: .
若给出顶点坐标和另一个点的坐标,设顶点式: .
若给出与x轴两交点的坐标和另一个点的坐标,设两点式:
探究新知
课堂小结
布置作业
创设情境
解:
设所求二次函数为 .
应用新知
巩固新知
随堂练习
1.求经过 , , 三点的抛物线的解析式.
由已知,函数图象经过 , , 得到关于 的三元一次方程组:
二次函数解析式为 .
探究新知
课堂小结
布置作业
创设情境
2.二次函数的图象如图,则它的解析式正确的是( )
O
y
x
2
2
A.
B.
C.
D.
(1,2)
x=1
解:
由图可知,二次函数的顶点坐标是(1,2),并且过点(2,0),因此设二次函数的解
析式为 ,带入,得
得
一般式为 .
应用新知
巩固新知
随堂练习
解析式为 ;
D
探究新知
课堂小结
布置作业
创设情境
2.二次函数的图象如图,则它的解析式正确的是( )
O
y
x
2
2
A.
B.
C.
D.
(1,2)
x=1
解:
解得
应用新知
巩固新知
随堂练习
D
由图可知,二次函数与x轴交点坐标是(2,0)和(0,0),又过(1,2)点,因此设解析式为 .
解析式为 .
解法二
探究新知
课堂小结
布置作业
创设情境
2.二次函数的图象如图,则它的解析式正确的是( )
O
y
x
2
2
A.
B.
C.
D.
(1,2)
x=1
解:
应用新知
巩固新知
随堂练习
D
解析式为 .
解法三
由图可知,二次函数与x轴交点坐标是(2,0)和(0,0),又过(1,2)点,因此设解析式为 .
解得
2.若给出顶点坐标和另一个点的坐标,设顶点式 .
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
1.若无特殊点,设一般式 .
待定系数法求
二次函数解析式
3.若给出与x轴两交点的坐标和另一个点的坐标,就设两点式 .
布置作业
教科书第42页练习第10-11题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
22.1 二次函数的图象和性质
1.4二次函数
的图象和性质(2)
学习目标
1.经历对用待定系数法求二次函数解析式的探究,掌握待定系数法求解析式的方法;
2.能灵活地根据条件恰当选取解析式,体会二次函数解析式之间的转化;
3.经历探究过程,培养学生数学运算的核心素养,并养成良好的运算习惯;
4.在学习过程中,感受学习数学知识的价值,提高对数学学习的兴趣.
重点
二次函数的图象性质
难点
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
我们知道,由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式.
一起探究
二次函数的解析式如何确定呢?
转 化
求得k,b的值
二元一次方程组
需要两点坐标
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
二次函数 的解析式中有几个待定系数?
3个待定系数
需要图象上的几个点?
3个点
转化成什么样的方程组?
三元一次方程组
创设情境
巩固新知
课堂小结
布置作业
设所求二次函数为 .
解:
二次函数 经过( ,10),(1,4),(2,7)三点,请求出这个二次函数的解析式.
例1:
由已知,函数图象经过( ,10),(1,4),(2,7)三点,得关于a,b,c的三元一次方程组
二次函数解析式为 .
探究新知
应用新知
典型例题
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
?
二次函数解析式
带入 三点坐标
三元一次方程组
求得a,b,c的值
例题总结
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
由已知,函数图象顶点坐标(1, ),且过B(2,1) 点,得关于a,h,k的方程
设所求二次函数为 .
应用新知
典型例题
二次函数解析式为 .
如果知道二次函数的顶点坐标为A(1, ),且过B(2,1) 点,请求出解析式.
例2:
创设情境
巩固新知
课堂小结
布置作业
二次函数解析式
带入 顶点+另一个点
方程
求得a的值
?
探究新知
应用新知
例题总结
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
如果知道二次函数的顶点坐标为A(1, ),且过B(2,1) 点,请求出解析式.
二次函数解析式为 .
应用新知
典型例题
例2:
设所求二次函数为 .
由已知,函数图象顶点坐标(1, ),且过B(2,1) 点,得
解法二
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
应用新知
典型例题
例3:
设所求二次函数为 .
解法一
二次函数解析式为 .
一个二次函数,当自变量 时,函数值 ,当 与 时, .求二次函数的解析式.
由已知,函数图象经过( 0 , ),( ,0),( ,0)得到关于 的三元一次方程组:
创设情境
巩固新知
课堂小结
布置作业
探究新知
解:
应用新知
典型例题
又∵抛物线过点(0, ),
解法二
设所求二次函数为 ,其中 .
由抛物线过点( , 0 ),( ,0)可知 , ;
∴解析式为 ;
∴ ,即 ;
二次函数为 .
例3:
一个二次函数,当自变量 时,函数值 ,当 与 时, .求二次函数的解析式.
便捷
创设情境
巩固新知
课堂小结
布置作业
二次函数解析式
带入 与x轴两交点+另一个点
方程
求得a的值
?
探究新知
应用新知
例题总结
创设情境
巩固新知
课堂小结
布置作业
探究新知
应用新知
例题总结
顶点式
两点式
一般式
若无特殊点,设一般式: .
若给出顶点坐标和另一个点的坐标,设顶点式: .
若给出与x轴两交点的坐标和另一个点的坐标,设两点式:
探究新知
课堂小结
布置作业
创设情境
解:
设所求二次函数为 .
应用新知
巩固新知
随堂练习
1.求经过 , , 三点的抛物线的解析式.
由已知,函数图象经过 , , 得到关于 的三元一次方程组:
二次函数解析式为 .
探究新知
课堂小结
布置作业
创设情境
2.二次函数的图象如图,则它的解析式正确的是( )
O
y
x
2
2
A.
B.
C.
D.
(1,2)
x=1
解:
由图可知,二次函数的顶点坐标是(1,2),并且过点(2,0),因此设二次函数的解
析式为 ,带入,得
得
一般式为 .
应用新知
巩固新知
随堂练习
解析式为 ;
D
探究新知
课堂小结
布置作业
创设情境
2.二次函数的图象如图,则它的解析式正确的是( )
O
y
x
2
2
A.
B.
C.
D.
(1,2)
x=1
解:
解得
应用新知
巩固新知
随堂练习
D
由图可知,二次函数与x轴交点坐标是(2,0)和(0,0),又过(1,2)点,因此设解析式为 .
解析式为 .
解法二
探究新知
课堂小结
布置作业
创设情境
2.二次函数的图象如图,则它的解析式正确的是( )
O
y
x
2
2
A.
B.
C.
D.
(1,2)
x=1
解:
应用新知
巩固新知
随堂练习
D
解析式为 .
解法三
由图可知,二次函数与x轴交点坐标是(2,0)和(0,0),又过(1,2)点,因此设解析式为 .
解得
2.若给出顶点坐标和另一个点的坐标,设顶点式 .
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
1.若无特殊点,设一般式 .
待定系数法求
二次函数解析式
3.若给出与x轴两交点的坐标和另一个点的坐标,就设两点式 .
布置作业
教科书第42页练习第10-11题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
